↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Next-token prediction (NTP) is the dominant training method for modern language models, but its optimization properties are not well understood. This paper investigates the optimization bias of NTP, particularly focusing on how different optimizers select solutions from the many possible minimizers of the objective function. A key challenge lies in understanding the impact of data sparsity, where each context is associated with a sparse probability distribution over tokens. The presence of many solutions makes it difficult to understand what properties of the training data lead to better generalization.
The researchers study this issue using linear models with fixed context embeddings, providing a more manageable setting to analyze the problem. They introduce “NTP-separability conditions” which guarantee that the training loss reaches its theoretical minimum. They also define a novel margin concept specific to the NTP setting and show that gradient descent, a common training algorithm, selects a direction dictated by the new margin. Their findings extend previous work on implicit bias in one-hot classification, highlighting key differences and demonstrating the effects of data sparsity on the optimization bias. The results provide valuable insights into the optimization and generalization properties of NTP and pave the way for further investigation into the design of more robust and interpretable language models. The study provides insights into the optimization bias of the widely used next-token prediction (NTP) paradigm, highlighting the impact of data sparsity and a novel margin concept. These findings extend our understanding of implicit bias in machine learning and pave the way for further research in designing more robust and interpretable language models.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in NLP and machine learning because it sheds light on the implicit biases in the widely used next-token prediction (NTP) training paradigm for language models. Understanding these biases is critical for improving model robustness, interpretability, and generalization. The findings also prompt further research into the optimization and generalization properties of NTP, irrespective of the architecture used.
Visual Insights#

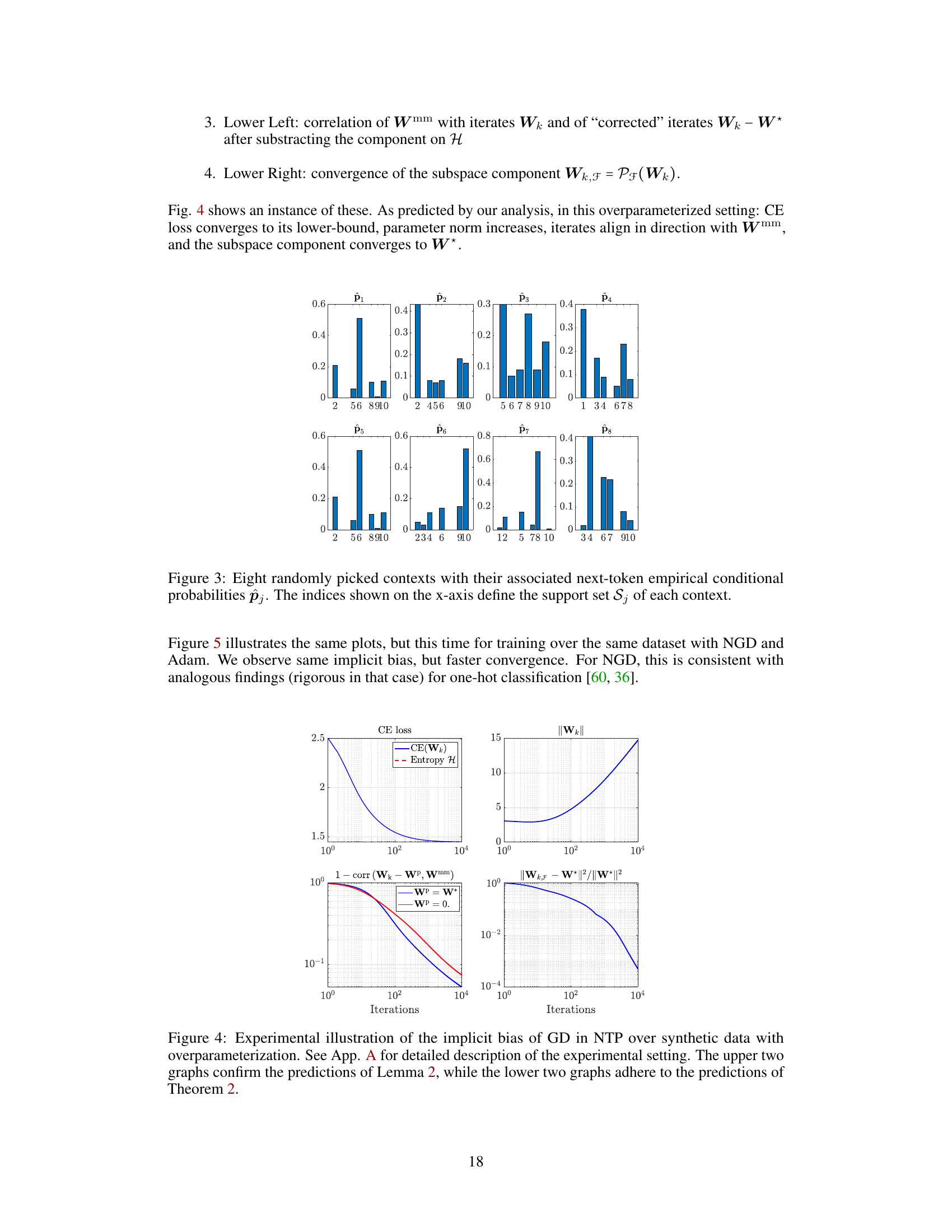
This figure visualizes the implicit optimization bias of next-token prediction (NTP) in a simplified setting. The left panel shows the geometry of context embeddings and word embeddings learned by gradient descent (GD). The word embeddings are visualized as vectors, with colors indicating which contexts they are most associated with. The right panel shows the convergence behavior of GD, confirming theoretical predictions about norm growth and directional alignment with the maximum-margin solution.
In-depth insights#
NTP Optimization Bias#
The concept of “NTP Optimization Bias” in the context of next-token prediction (NTP) language models refers to the inherent tendency of gradient-based optimizers to select specific solutions from a potentially infinite set of loss-minimizing parameters. This bias isn’t explicitly programmed but emerges from the interaction of the optimization algorithm and the structure of the objective function. The paper investigates this bias by framing NTP as cross-entropy minimization across distinct contexts and sparse probability distributions. It introduces “NTP-separability” conditions that determine when the data entropy lower bound is reachable, characterizing how gradient descent selects parameters to meet these conditions within and orthogonal to the data subspace. This highlights a key difference between the NTP setting and traditional one-hot classification, where implicit bias has been more thoroughly studied. The findings extend prior research by introducing a novel margin concept specifically for NTP and showing how it influences the implicit bias of gradient descent. Crucially, the study emphasizes how context sparsity and repetition within training data interact with the optimizer to shape this bias. Ultimately, the paper suggests this bias is deeply linked to a tradeoff between finite-norm parameter solutions and infinite margin maximization within distinct subspaces defined by the training data.
Data Separability#
Data separability, in the context of machine learning, is a crucial concept that significantly impacts model performance and generalizability. It refers to the degree to which different classes or groups within a dataset are distinct and easily distinguishable. High data separability implies that the classes are well-separated in feature space, leading to easier classification and potentially higher accuracy, with models rapidly converging to a solution. Conversely, low data separability indicates overlapping classes that are difficult to distinguish. This presents challenges for model training, as the model may struggle to accurately classify instances, potentially resulting in poor generalization to unseen data and higher error rates. The notion of separability is also closely tied to the choice of model architecture and the nature of the features used. For instance, linear models assume linear separability, while more complex models can, in theory, capture non-linear relationships between features. The level of separability is inherent in the data itself, and choosing features that maximize separability often requires domain expertise and careful feature engineering. Therefore, understanding and addressing data separability is essential for successful machine learning, affecting both the selection of algorithms and feature preparation strategies.
Margin Concept#
The concept of margin, crucial in classification, is thoughtfully extended to the next-token prediction (NTP) setting. Traditional margins focus on separating data points of different classes; however, in NTP, the challenge lies in separating the likely next tokens from the unlikely ones within the context of a given sequence. This necessitates a nuanced definition of margin that accounts for the inherent sparsity of token probability distributions. The authors cleverly introduce a margin concept that addresses the distribution of next tokens conditional on the context. This allows them to relate the newly defined margin to optimization and to analyze the optimization bias of gradient descent. The margin, thus defined, is shown to guide the directional convergence of the algorithm, providing a valuable tool to understand implicit bias in training language models with the NTP paradigm. The resulting analysis reveals a connection between maximizing this margin and the model’s convergence to a data subspace where the logits’ differences align with token log-odds, highlighting a crucial aspect of implicit regularization in modern language models.
GD Implicit Bias#
The study delves into the implicit bias of gradient descent (GD) in the context of next-token prediction (NTP), a dominant training paradigm for language models. It reveals that GD’s optimization path exhibits a specific bias, particularly in overparameterized settings where many solutions minimize the training loss. The key finding is the characterization of this bias, which is shown to converge to a direction that maximizes a margin specific to the NTP objective. This margin is defined in relation to the sparsity patterns within the training data, highlighting a connection between the training data’s structure and GD’s inherent preferences. The analysis extends previous research on implicit bias, emphasizing the unique challenges posed by NTP’s sequential nature and the repeated occurrence of contexts. The resulting theoretical framework provides novel insights into the optimization dynamics of language models, regardless of the specific architecture used for generating context embeddings. Importantly, the study’s findings extend beyond linear models, suggesting broader implications for understanding how various language models learn and generalize.
Future Research#
The paper’s ‘Future Research’ section highlights several crucial avenues for extending this work. Addressing the limitations of the current linear model by incorporating non-linear architectures and exploring the impact of different embedding methods, such as those used in transformers, is vital. The authors also suggest delving deeper into the generalization properties of the NTP-SVM solution, potentially by developing novel statistical models for context embeddings and better metrics for generalization in the context of language modeling. Furthermore, a more thorough investigation into the impact of overparameterization is needed, which includes determining more precise thresholds for NTP-separability and exploring how this affects the optimization landscape. Finally, investigating the optimization bias of other algorithms beyond gradient descent and analyzing the effects of different training objectives is warranted. Overall, the paper lays a strong foundation that opens up exciting possibilities for advancing the understanding of next-token prediction models, and these future research directions are key to unlocking a more complete theory of implicit regularization.
More visual insights#
More on figures
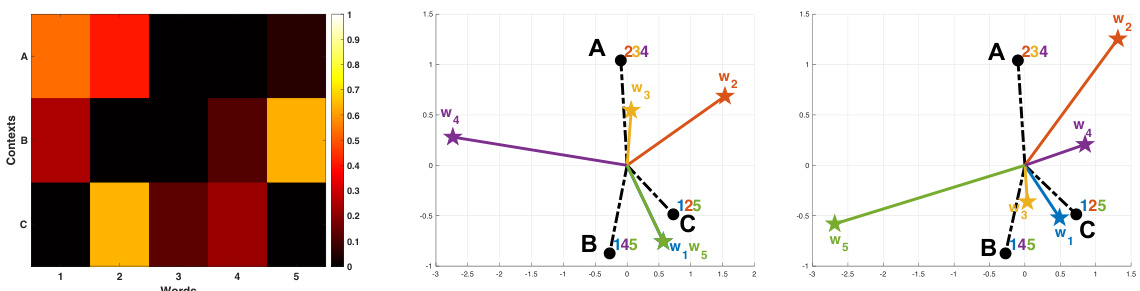
This figure visualizes the implicit optimization bias of next-token prediction (NTP) in a simple setting. The left panel shows the context embeddings and word embeddings learned by gradient descent (GD), illustrating how the geometry reflects the support sets and conditional probabilities of the next tokens. The right panel shows that gradient descent (GD) aligns with the maximal margin direction, and the finite component converges to a solution that equates logits differences of in-support tokens to their log-odds, demonstrating the implicit bias of GD in NTP.
This figure illustrates the implicit optimization bias of next-token prediction (NTP) in a simple setting. The left panel shows the context embeddings and the corresponding word embeddings learned by gradient descent. The right panel shows the convergence behavior of the gradient descent algorithm, demonstrating the alignment with the max-margin direction and convergence to a specific solution in a data subspace.

This figure visualizes the implicit optimization bias of next-token prediction (NTP) in a simple setting. The left panel shows the geometry of context embeddings and word embeddings learned by gradient descent. The right panel shows the training loss, norm growth of the weight matrix, alignment with the max-margin vector, and convergence of the weight matrix to a specific subspace.

The figure visualizes the implicit optimization bias of next-token prediction (NTP) using a simple setting with 3 distinct contexts, 2D embedding space, and a vocabulary of 5 words. The left panel shows the context embeddings and their associated support sets, illustrating the geometry of word embeddings learned by NTP training and how they relate to context embeddings. The right panel shows the results of gradient descent (GD) training in terms of loss, norm growth, alignment with the max-margin vector, and convergence to the subspace projection.
Full paper#