Towards Human-AI Complementarity with Prediction Sets

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on human-AI collaboration and decision support systems. It addresses a critical gap by demonstrating the suboptimality of existing conformal prediction methods for constructing prediction sets and offers a novel, efficient greedy algorithm that significantly improves performance. This work paves the way for more effective decision support systems that enhance human expertise and opens new avenues for research into optimal prediction set design and efficient approximation algorithms.

Visual Insights

#

The figure illustrates the automated decision support system’s workflow. A data sample (e.g., an X-ray image) with features x is input. The decision support system processes this and provides a prediction set S(x), which is a subset of all possible labels Y. The human expert then reviews this narrowed set of potential labels and makes a prediction ŷ, which must be selected from the S(x) set.

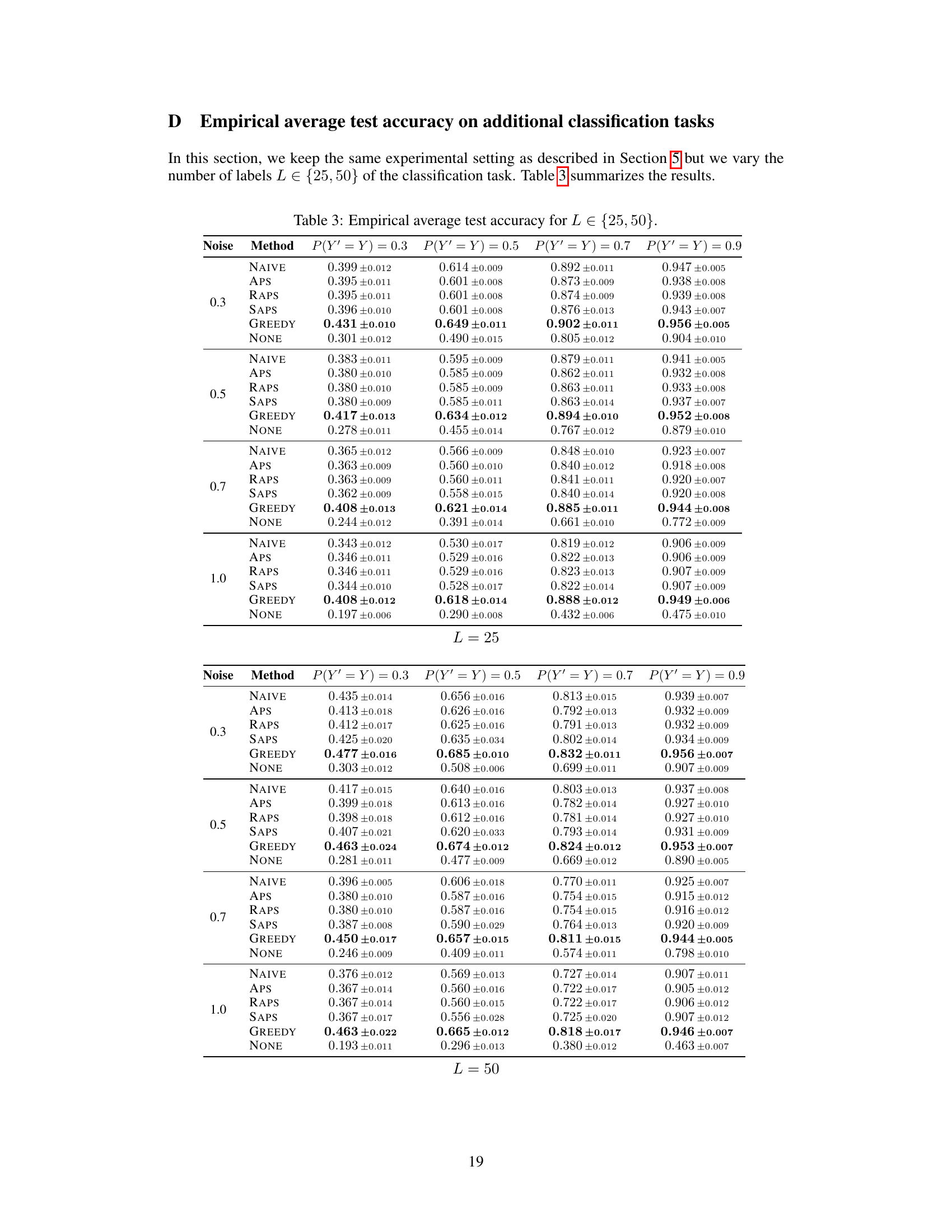
This table presents the results of a simulation study comparing the average accuracy of four simulated human experts using prediction sets generated by different methods. The methods include conformal prediction with four different non-conformity scores (NAIVE, APS, RAPS, SAPS) and a novel greedy algorithm (GREEDY). The table shows the average accuracy of each expert for four different classification tasks and four noise levels (γ). The best performing method for each scenario is highlighted in bold.

In-depth insights

#

Conformal Limits

#

The heading ‘Conformal Limits’ suggests an exploration of the boundaries and constraints within conformal prediction methods. A thoughtful analysis would delve into the theoretical limitations of conformal prediction, such as its computational complexity for high-dimensional data or the assumptions underlying its validity (e.g., i.i.d. data). Practical limitations might include the sensitivity of conformal prediction’s performance to the choice of non-conformity measure, the size of the calibration set, or the characteristics of the underlying data distribution. Investigating these limits could involve examining scenarios where conformal prediction fails to provide accurate or reliable prediction sets and exploring potential modifications or alternative approaches to address these shortcomings. A comprehensive discussion would also evaluate the trade-offs between the conformal prediction’s properties (e.g., validity and efficiency) and its performance in practice. This could involve comparing conformal prediction to other uncertainty quantification methods and analyzing their relative strengths and weaknesses under various conditions.

Greedy Optimization

#

A greedy optimization approach in this context likely involves iteratively selecting the locally optimal prediction set at each step, without considering the global optimum. This strategy prioritizes immediate gains in expert accuracy, potentially sacrificing overall performance for computational efficiency. The algorithm’s effectiveness hinges on the nature of expert prediction behavior and the non-conformity score used. A well-chosen non-conformity score, sensitive to expert accuracy, is crucial. If this score poorly reflects expert performance, the greedy approach may fail to improve accuracy compared to conformal prediction. The NP-hardness result suggests that finding the absolute best prediction sets is computationally intractable, thus justifying the greedy strategy’s practicality. However, the algorithm’s theoretical guarantees depend on satisfying specific conditions regarding the expert models and non-conformity scores; failure to meet these conditions could compromise its performance. Empirical evaluation is key to determine whether the greedy algorithm provides a substantial improvement in real-world scenarios. The success of this method lies in its ability to strike a balance between optimizing accuracy and managing computational cost. Future research might investigate approximation bounds for the greedy approach, identifying when it reliably yields near-optimal solutions.

Synthetic & Real Data

#

The use of both synthetic and real-world datasets is a strength of this research. Synthetic data allows for controlled experiments to isolate the effects of specific variables and test the algorithm’s performance under diverse conditions. The authors can systematically manipulate factors like noise levels or expert accuracy. However, real-world datasets are crucial for evaluating the algorithm’s generalizability and practical effectiveness in situations mirroring actual applications. The combination provides a comprehensive assessment, validating the method’s theoretical properties with empirical evidence from realistic scenarios. The results reveal that the algorithm consistently outperforms existing methods, demonstrating robust performance across diverse settings. A limitation, however, could be the generalizability of results from the synthetic data to real-world complexity. Future research might investigate the algorithm’s ability to handle highly noisy data or diverse human expertise more effectively.

Human-AI Synergy

#

Human-AI synergy explores the collaborative potential between humans and artificial intelligence, aiming to leverage the strengths of each to achieve superior outcomes than either could accomplish alone. Humans offer intuition, creativity, and complex reasoning, while AI provides speed, data processing power, and pattern recognition. Successful synergy requires careful design of the human-AI interaction, considering human factors and cognitive biases to ensure effective communication and task allocation. A key aspect is the transparency and explainability of AI’s decision-making process, allowing humans to understand and trust the AI’s contributions. Challenges include defining appropriate levels of automation and ensuring equitable distribution of tasks. Ethical concerns surrounding bias and accountability must also be addressed, as AI’s role expands in decision-making processes. The ultimate goal is to create systems where humans and AI are true partners, complementing each other’s capabilities to solve complex problems.

Future Work

#

Future research directions stemming from this work could explore relaxing the strong assumptions made about expert behavior. The current model assumes experts follow a mixture of multinomial logit models; a model-free approach would enhance generalizability. Investigating alternative non-conformity scores that incorporate expert prediction distributions could also improve prediction set generation. Additionally, robustness to noisy labels and model misspecification should be investigated. The scalability of the greedy algorithm for extremely large datasets requires further attention. Finally, exploring applications in high-stakes domains and accounting for fairness and safety are critical considerations for impactful future research.

More visual insights

#

More on figures

This figure illustrates the automated decision support system proposed in the paper. It shows how, given an input data sample with features (x), a classifier (C) helps the human expert by reducing the number of possible label values to consider. The classifier provides a prediction set (S(x)) which is a subset of all possible labels (Y). The human expert then makes a prediction (ŷ) from within this smaller set of possibilities.

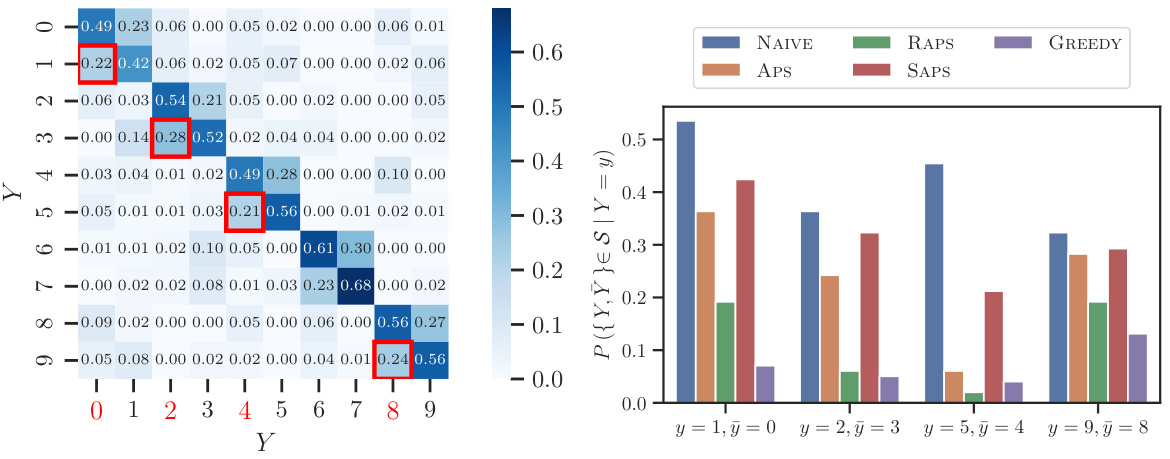
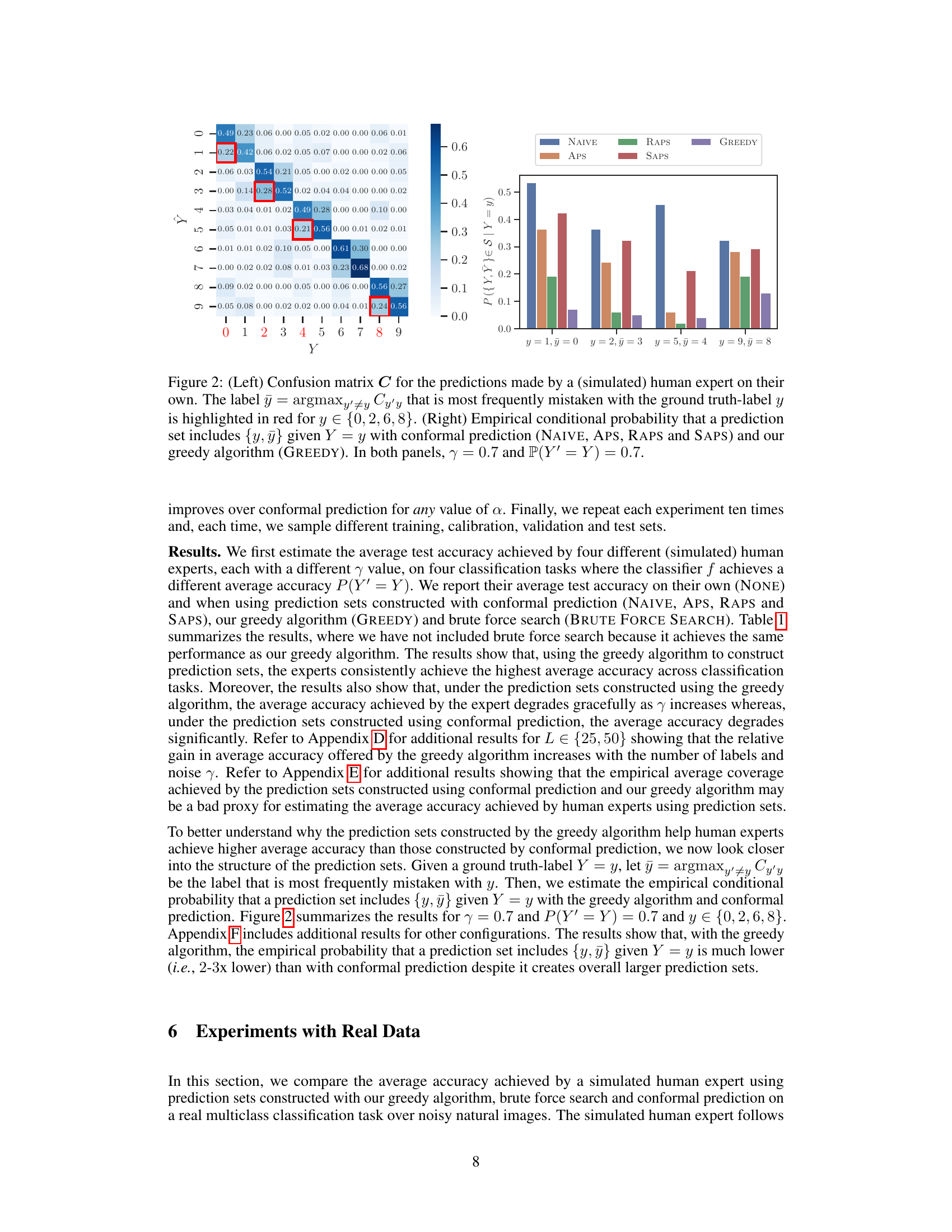
This figure shows two plots. The left plot is a confusion matrix that visualizes the errors made by a simulated human expert in a multi-class classification problem. Each cell (i, j) represents the probability of the expert predicting class j when the true class is i. The right plot shows the empirical conditional probability that a prediction set includes the true label y and the most frequently mistaken label ÿ given the true label is y. This probability is computed for different prediction set construction methods: conformal prediction (NAIVE, APS, RAPS, SAPS) and a greedy algorithm (GREEDY). The results indicate that the greedy algorithm leads to prediction sets that include the true and most commonly confused labels less often compared to conformal methods.

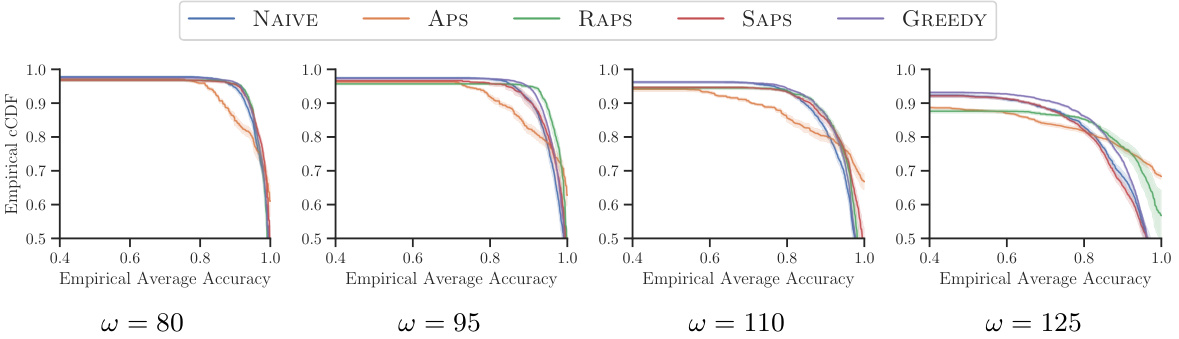
This figure compares the performance of different methods for constructing prediction sets in a multi-class classification task using the ImageNet16H dataset. The x-axis represents the empirical average accuracy achieved by a simulated human expert using the prediction sets, and the y-axis represents the complementary cumulative distribution function (cCDF) of the per-image test accuracy. The plot shows that the prediction sets generated by the greedy algorithm consistently outperform those generated by various conformal prediction methods (NAIVE, APS, RAPS, SAPS) across different noise levels (ω). The results indicate that the greedy algorithm is more effective at improving human expert accuracy.

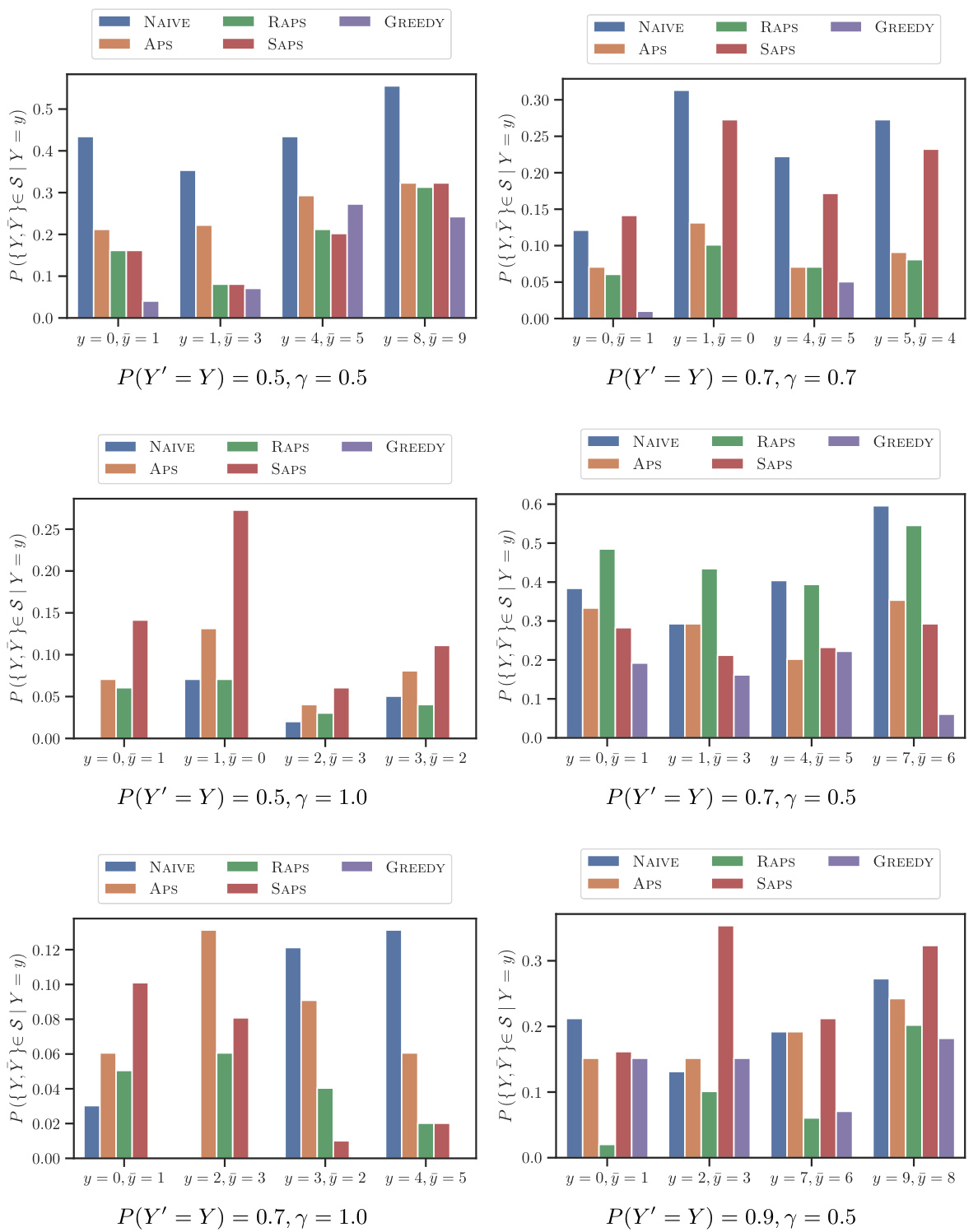
The left panel shows the confusion matrix for predictions made by a simulated human expert. The right panel shows the conditional probability that a prediction set contains both the true label and the label most often confused with the true label, given different methods for creating prediction sets. The results indicate a lower probability of this event happening when using the proposed greedy algorithm.

This figure compares the average accuracy of a simulated human expert whose predictions follow a mixture of multinomial logit models (MNLs) and that of real human experts. The prediction sets used were generated by conformal predictors with varying α values, using a calibration set selected by Straitouri et al. [19]. The graph shows that while the MNL model overestimates the accuracy, the general trend of accuracy across different α values is similar for both the simulated and real human experts. The peak average accuracy for both groups is highlighted in red.

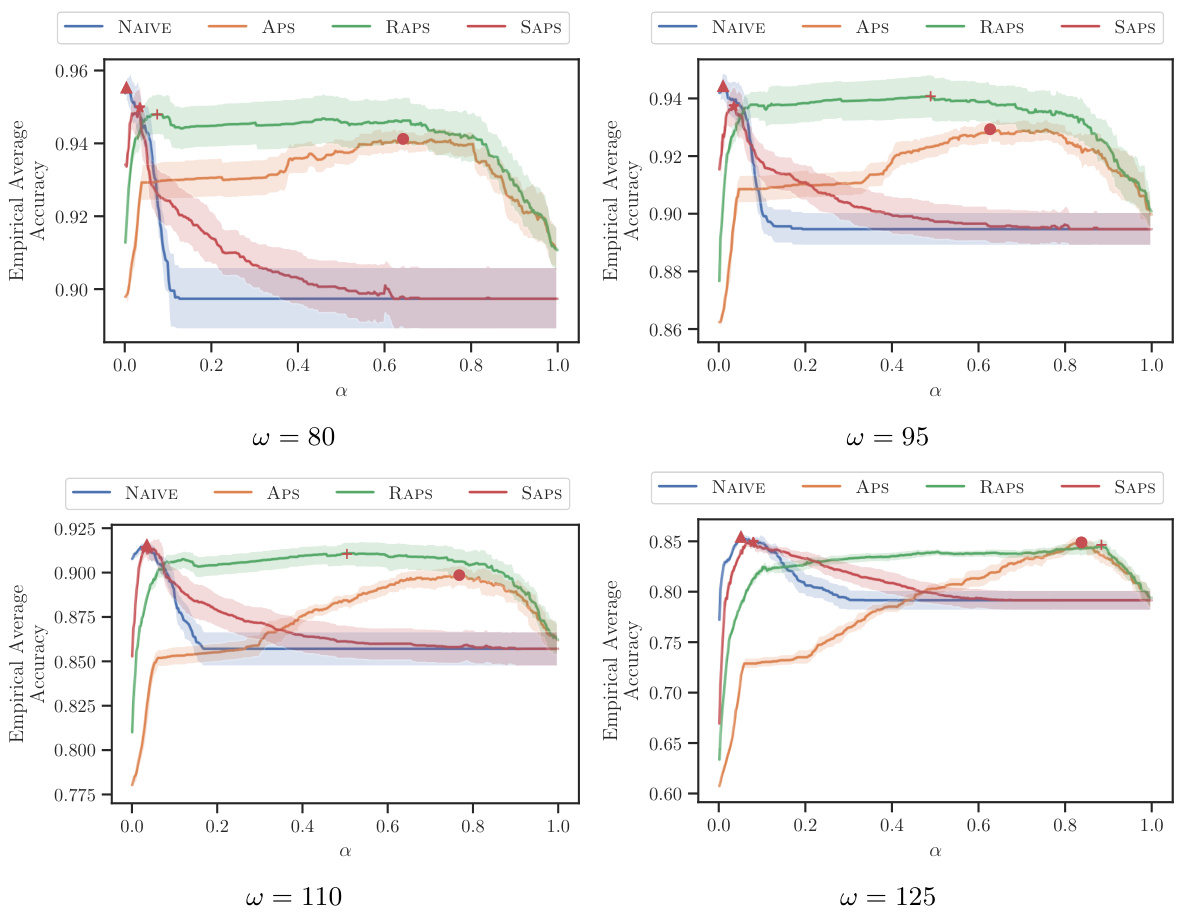
This figure displays the average accuracy achieved by a simulated human expert using prediction sets constructed by four different conformal prediction methods (NAIVE, APS, RAPS, SAPS) on the ImageNet16H dataset. The x-axis represents the α value used in the conformal prediction, and the y-axis represents the average accuracy. Each panel corresponds to a different level of noise (ω) in the ImageNet16H dataset. Error bars representing standard error are included. The highest average accuracy for each method is highlighted with a red marker, illustrating the optimal α value for each conformal predictor under different noise levels.

More on tables

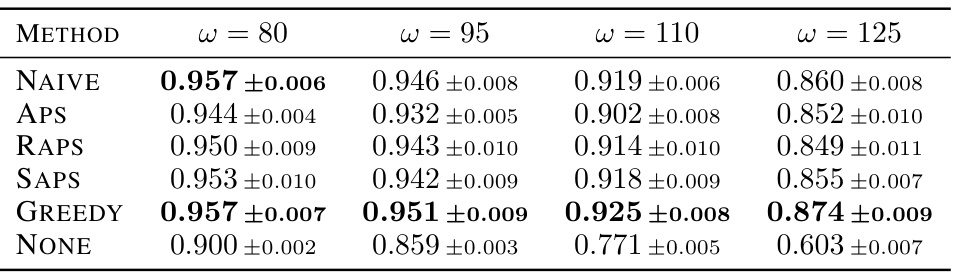
This table presents the average test accuracy achieved by simulated human experts using different prediction set construction methods on the ImageNet16H dataset. The methods compared include four types of conformal prediction (NAIVE, APS, RAPS, SAPS) and a greedy algorithm (GREEDY). The table shows the average accuracy for each method across four different noise levels (ω = 80, 95, 110, 125), along with the standard deviation across 10 runs. The best performing method for each noise level is highlighted in bold. A baseline is also provided (NONE), showing the human expert’s accuracy without the aid of a prediction set.

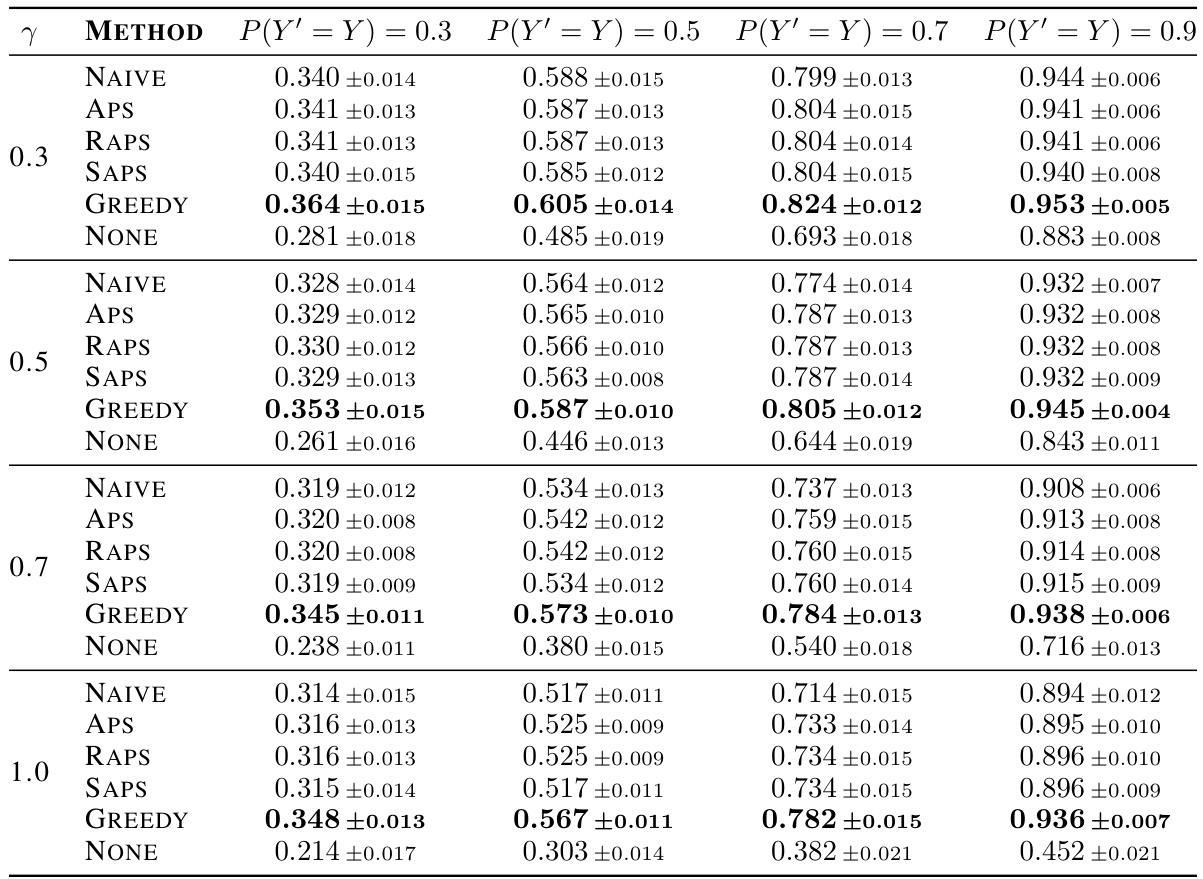
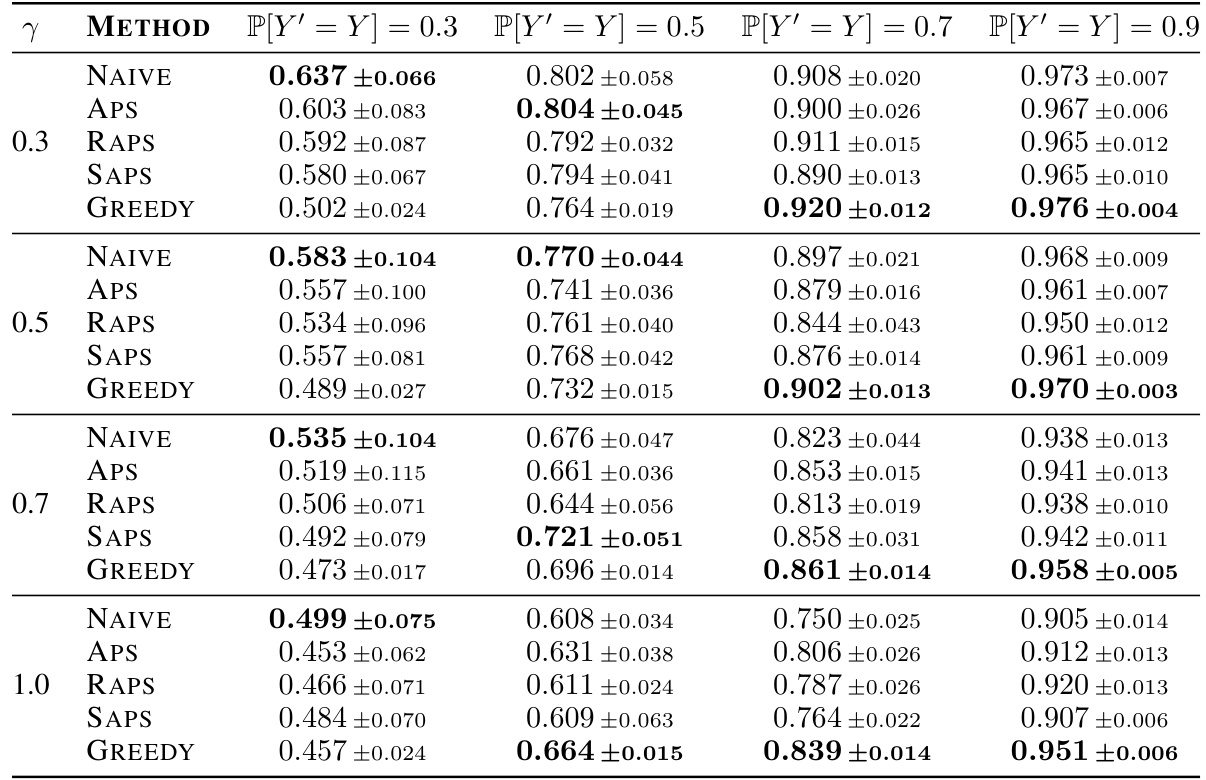
This table presents the average test accuracy achieved by four simulated human experts with varying levels of noise (γ) using different methods to construct prediction sets. It compares the performance of the experts using prediction sets from conformal prediction methods (NAIVE, APS, RAPS, SAPS) and the greedy algorithm, against the experts’ performance without any prediction sets (NONE). The results are averaged over 10 runs for each classification task, with the best performing method highlighted in bold.

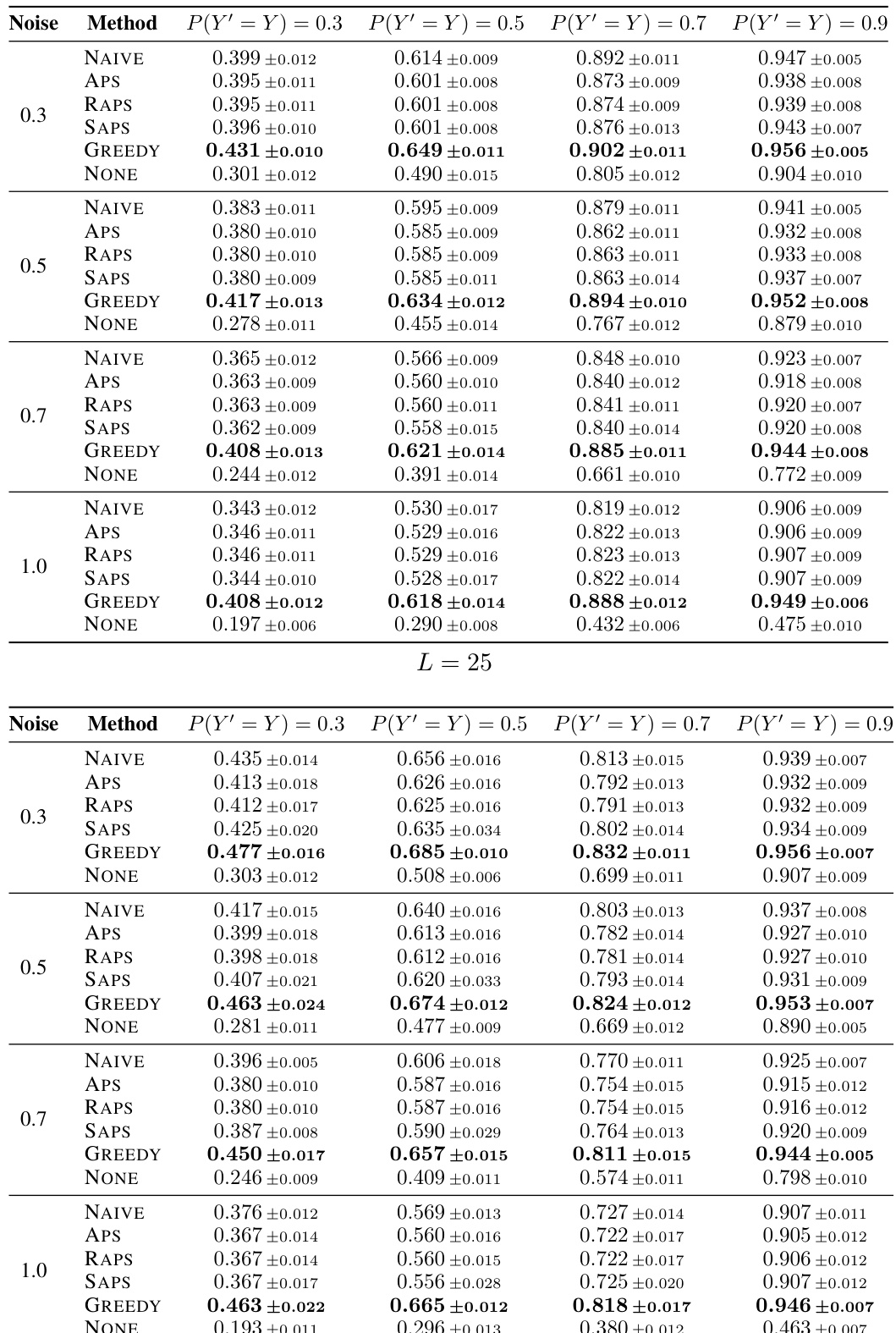
This table presents the average test accuracy achieved by four simulated human experts with varying levels of noise (γ) using different methods for constructing prediction sets. It compares the accuracy of the experts making predictions on their own (NONE) to the accuracy when using prediction sets from conformal prediction methods (NAIVE, APS, RAPS, SAPS) and the proposed greedy algorithm (GREEDY). The results are shown for four synthetic classification tasks with different classifier accuracies (P(Y’=Y)) and highlight the superior performance of the greedy algorithm.

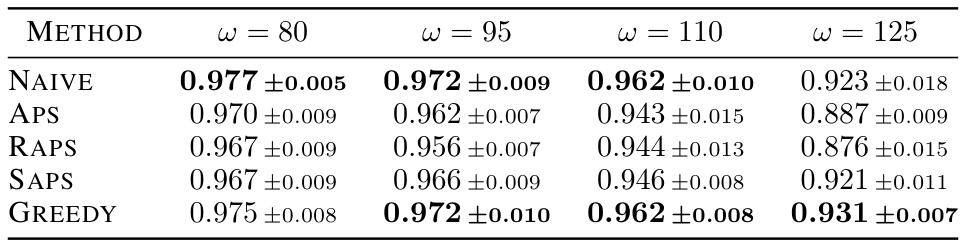
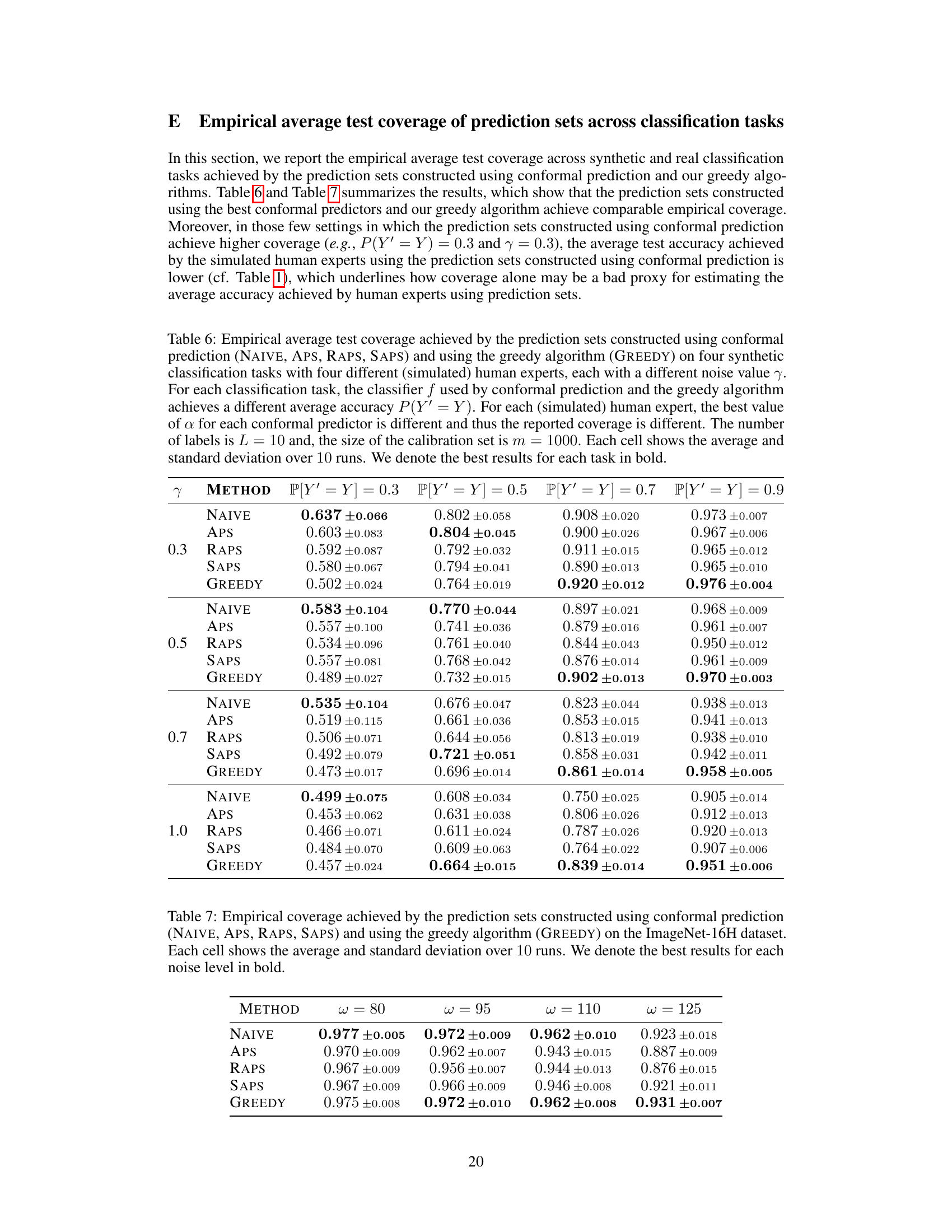
This table presents the empirical average test coverage achieved by prediction sets generated using different methods across four noise levels in the ImageNet16H dataset. The methods include four conformal prediction approaches (NAIVE, APS, RAPS, SAPS) and the proposed greedy algorithm (GREEDY). The table highlights the average coverage and standard deviation across 10 runs for each method and noise level, indicating the consistency of coverage performance. Bold values indicate the best coverage obtained for each noise level.

Full paper

#