↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline-to-online (O2O) reinforcement learning aims to leverage pre-trained offline policies for faster online learning. However, existing methods often struggle with inconsistencies between offline datasets and online environments, leading to unstable performance. This paper identifies two key problems: evaluation and improvement mismatches. Evaluation mismatches arise from differences in how policies are evaluated offline and online; improvement mismatches stem from inconsistencies in how policies are updated.
This paper proposes a general framework, OCR-CFT, to address these mismatches. First, it re-evaluates the offline policy optimistically to avoid performance drops during initial online fine-tuning. Second, it calibrates the critic to align with the offline policy to prevent errors during policy updates. Finally, it uses constrained fine-tuning to handle distribution shifts. Experiments demonstrate that OCR-CFT achieves significant and stable performance improvements on multiple benchmark tasks, surpassing the performance of state-of-the-art O2O methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for reinforcement learning researchers because it tackles the challenge of general offline-to-online RL, a significant hurdle in deploying RL agents in real-world scenarios. The proposed solution addresses evaluation and improvement mismatches, offering a more robust and efficient approach. This has potential to boost the performance of RL applications across various domains, especially in safety-critical settings.
Visual Insights#

This figure compares the performance of actors updated with three different critics: a fixed re-evaluated critic, an iteratively re-evaluated critic (which updates with the policy), and the proposed aligned critic. The results show that the performance of the re-evaluated critics sharply declines at the initial stage and does not recover, while the aligned critic achieves stable and favorable performance. This highlights the importance of aligning the critic with the offline policy for effective online fine-tuning.

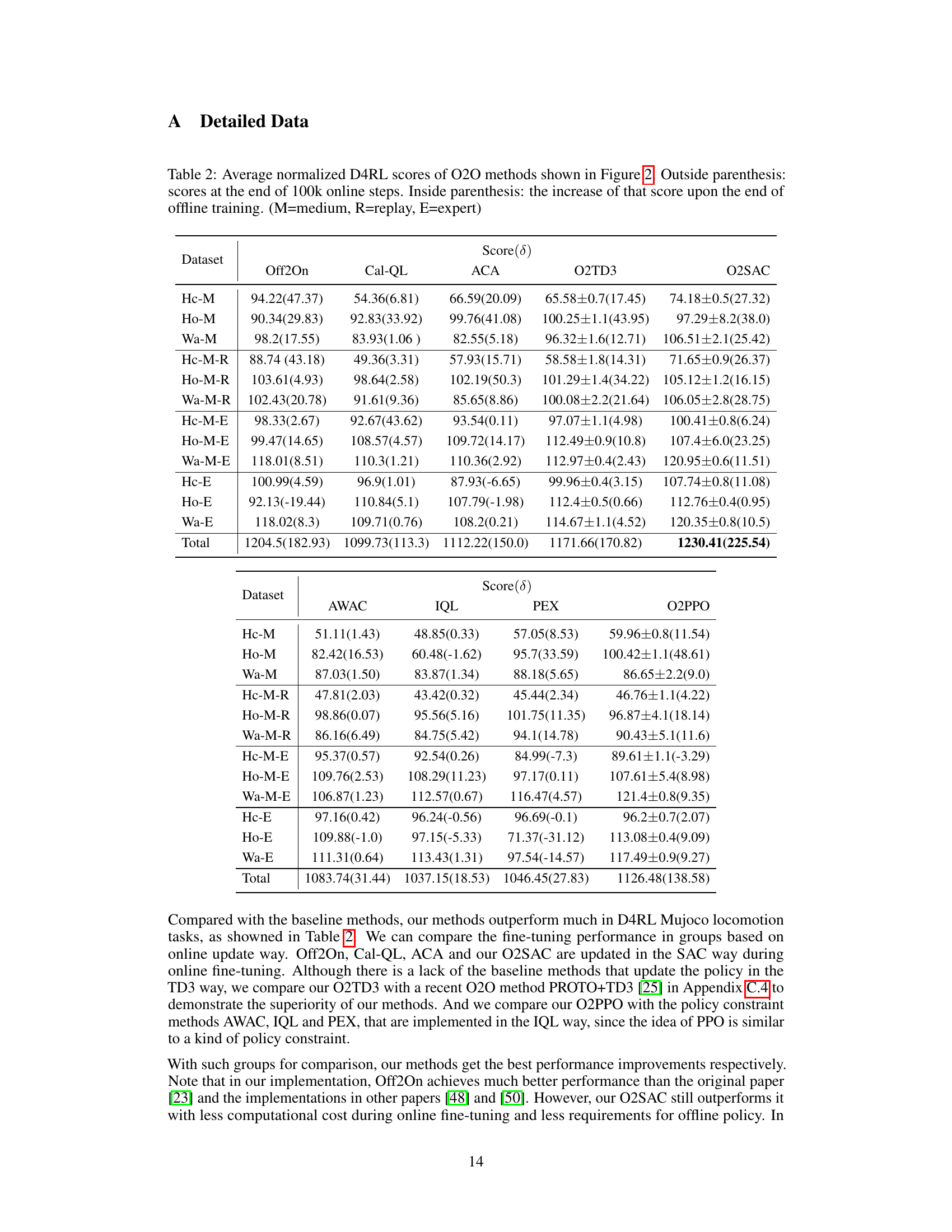
This table presents the average normalized D4RL scores achieved by various offline-to-online (O2O) reinforcement learning methods on AntMaze navigation tasks. The scores are obtained after 200,000 interactions with the environment. The table compares the proposed O2O methods (O2TD3, O2SAC, O2PPO) against existing methods (IQL, PEX, Cal-QL). The results are divided into two AntMaze variations (U-v2 and U-D-v2) and an overall total score. The notation U-v2 represents the umaze task, and U-D-v2 the umaze diverse task. The scores are presented as ranges, reflecting the performance variation across different runs.
In-depth insights#
O2O RL Mismatches#
The core concept of Offline-to-Online Reinforcement Learning (O2O RL) involves leveraging pre-trained offline policies to enhance online learning. However, a critical challenge arises from mismatches between the offline data and the online environment. The paper highlights two key types of mismatches. Evaluation mismatches stem from discrepancies in policy evaluation methods used during offline and online phases, leading to unstable Q-value estimations and potentially hindering performance. Improvement mismatches occur due to inconsistencies in the objectives used to update policies, causing a misalignment between action probabilities and their associated Q-values. Addressing these mismatches is crucial for achieving robust and efficient O2O RL, enabling effective general O2O learning from diverse offline to online algorithms. The proposed method directly tackles these issues by using off-policy evaluation for optimistic critic estimation and value alignment to bridge the gap between actor and critic, ultimately leading to more stable and improved online performance.
Optimistic Critic#
The concept of an “Optimistic Critic” in reinforcement learning addresses the limitations of pessimistic critics, which often underestimate the value of actions, leading to overly cautious policies. Optimistic critics aim to counteract this pessimism by providing more favorable evaluations of actions, potentially leading to more exploratory behavior and faster learning. This is achieved through various techniques, such as modifying the reward function, adjusting the update rules, or using ensemble methods. While optimism can accelerate learning, it also introduces the risk of overestimation, causing instability and potentially poor generalization. Therefore, a well-designed optimistic critic needs to balance exploration and exploitation effectively, avoiding overly optimistic estimates that lead to poor performance. The effectiveness of an optimistic critic depends heavily on the specifics of its implementation and the characteristics of the environment. Careful consideration of the trade-off between optimism and stability is crucial for successfully applying this approach in reinforcement learning tasks.
Value Alignment#
The concept of ‘Value Alignment’ in offline-to-online reinforcement learning (RL) addresses a critical mismatch between the learned policy’s preferences (represented by action probabilities) and the critic’s evaluation of those actions (Q-values). Before online fine-tuning, this mismatch can lead to unstable or poor performance, because the policy updates might be guided by inaccurate or conflicting value estimations. The proposed value alignment techniques aim to bridge this gap by calibrating the critic’s Q-values to better reflect the policy’s preferences. This often involves using the Q-value of the most likely action as an anchor and then adjusting the Q-values of other actions, leveraging either the correlations between different state-action pairs or modeling the Q-values using a Gaussian distribution. The goal is to ensure that actions favored by the policy also receive high Q-values, promoting a harmonious feedback loop between the actor and the critic during online learning and leading to improved stability and faster convergence.
Constrained Tuning#
Constrained fine-tuning addresses the critical challenge of distribution shift between offline and online reinforcement learning environments. The core idea is to prevent the online policy from diverging significantly from the well-trained offline policy, which provides a reliable initialization but may not generalize perfectly to unseen online data. This is achieved by imposing constraints or penalties on the online policy update, encouraging it to remain within a region of the state-action space similar to what the offline policy experienced, mitigating instability and enabling safe and effective online improvement. Regularization techniques, such as KL divergence or MSE loss, are commonly used to quantify the deviation from the offline policy, preventing overly drastic updates and enhancing robustness. The specific constraints are often carefully tuned to find the balance between utilizing the offline knowledge and exploring new areas in the online environment for optimal performance. The success of constrained fine-tuning heavily depends on the quality of the offline dataset and the appropriate choice of the regularization method and its hyperparameters, reflecting the inherent trade-off between exploration and exploitation in the online learning phase.
Generalizability#
The generalizability of offline-to-online reinforcement learning (RL) methods is a critical concern. Many existing methods are tailored to specific offline algorithms, limiting their broad applicability. A truly generalizable approach should seamlessly integrate with various offline techniques, regardless of their underlying methodology (e.g., value regularization, policy constraint). The paper addresses this challenge by identifying and resolving two key mismatches: evaluation mismatches (differences in policy evaluation methods between offline and online settings) and improvement mismatches (discrepancies in policy update objectives). By introducing techniques like optimistic critic reconstruction and value alignment, the proposed framework aims to bridge these mismatches and achieve consistent improvement across multiple offline and online RL algorithms. The success of this generalized approach hinges on its ability to handle the inevitable distribution shift during the transition from offline to online environments. This is addressed using constrained fine-tuning, a method that ensures stable updates and prevents the policy from deviating drastically from its reliable offline counterpart. The empirical results offer strong evidence of the method’s effectiveness across a range of simulated tasks; however, future work should evaluate the proposed framework on real-world applications to establish its true generalizability and robustness.
More visual insights#
More on figures
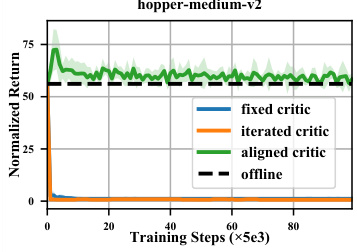
This figure compares the performance of three different critics in online reinforcement learning: a fixed re-evaluated critic, an iteratively re-evaluated critic, and an aligned critic. The results show that the fixed and iterated critics experience a sharp decline in performance at the beginning of online training, while the aligned critic maintains stable and favorable performance. This highlights the importance of aligning the critic with the offline policy for effective online fine-tuning.

This figure shows the performance curves of various offline-to-online reinforcement learning (RL) methods on several MuJoCo locomotion tasks from the D4RL benchmark. The x-axis represents the number of evaluation epochs during online fine-tuning, and the y-axis represents the normalized return achieved by each method. The figure allows comparison of the proposed methods (O2SAC, O2TD3, O2PPO) against existing state-of-the-art methods (AWAC, IQL, PEX, Off2On, Cal-QL, ACA). The different colored lines and shaded areas represent the mean and standard deviation across multiple runs for each method, highlighting the performance consistency and stability of each algorithm on the tasks.
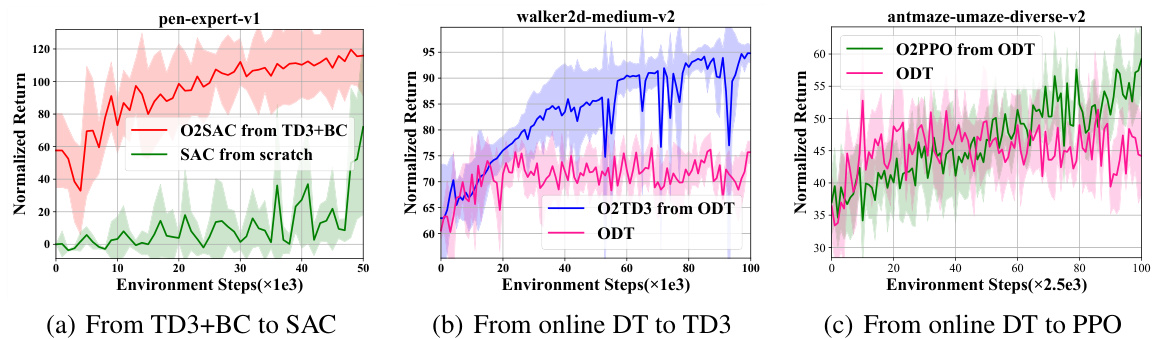
This figure demonstrates the transferability of the proposed O2O method. Three online RL algorithms (SAC, TD3, and PPO) are fine-tuned using offline policies trained with different offline RL methods (TD3+BC, ODT). The results illustrate that the proposed method consistently improves online performance, showing that the method is not dependent on the specific offline algorithm used.

This figure compares the online fine-tuning performance of the proposed O2PPO method with a direct application of PPO initialized from an IQL offline policy. The results are shown across multiple MuJoCo locomotion tasks from the D4RL benchmark. The plots show the normalized return over evaluation epochs. The solid lines represent the average performance across multiple runs, and the shaded regions indicate the standard deviation, illustrating the stability and variability of the methods.

This figure presents ablation studies evaluating the impact of each component of the proposed O2O (Offline-to-Online) RL method on several MuJoCo locomotion tasks. The components are Policy Re-evaluation (PR), Value Alignment (VA), and Constrained Fine-tuning (CF). Each subfigure shows the performance curves for a specific task and algorithm (O2SAC, O2TD3, and O2PPO), comparing the full method with versions missing one or more components. The results demonstrate the contribution of each component to the overall stable and efficient performance improvement.

This figure shows the performance curves of different offline-to-online reinforcement learning methods on several MuJoCo locomotion tasks from the D4RL benchmark. The x-axis represents the number of evaluation epochs during online fine-tuning, and the y-axis represents the normalized return achieved by each method. The figure visually compares the performance of the proposed O2O RL methods (O2SAC, O2TD3, O2PPO) against several state-of-the-art baselines (AWAC, IQL, PEX, Off2On, Cal-QL, ACA). The shaded area around each line represents the standard deviation across multiple runs.

This figure displays the performance curves of various offline-to-online reinforcement learning (RL) methods on several MuJoCo locomotion tasks from the D4RL benchmark. The x-axis represents the number of evaluation epochs during online fine-tuning, and the y-axis shows the normalized return achieved by each method. Multiple methods are compared, including the proposed approach (O2SAC, O2TD3, and O2PPO) and several state-of-the-art baselines (AWAC, IQL, PEX, Off2On, Cal-QL, and ACA). The figure visualizes the stability and efficiency of each method’s performance improvement during online fine-tuning on different tasks (with medium, replay, and expert datasets).
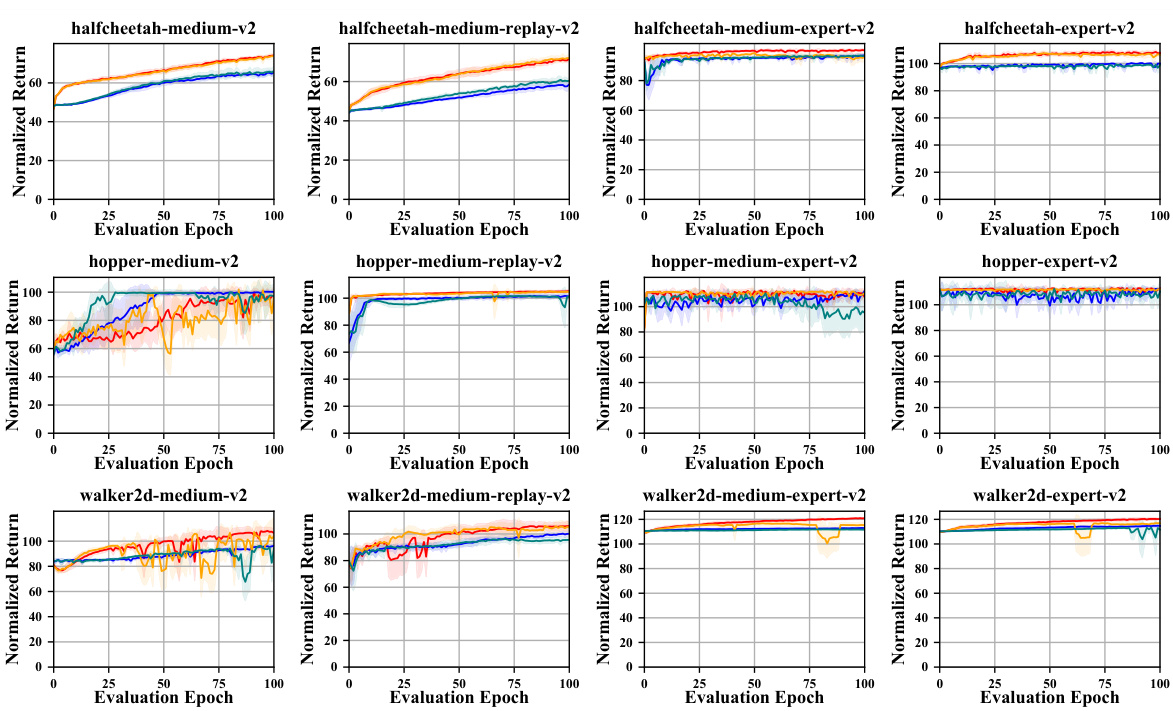
This figure displays the performance of various offline-to-online reinforcement learning (RL) methods across multiple MuJoCo locomotion tasks from the D4RL benchmark. Each sub-plot represents a specific task (e.g., HalfCheetah, Hopper, Walker2d) and dataset variation (medium, replay, expert). The x-axis shows the number of evaluation epochs during online fine-tuning, and the y-axis represents the normalized return. The curves compare the performance of the proposed method (O2SAC, O2TD3, O2PPO) with existing state-of-the-art methods. The figure illustrates the stability and efficiency of the proposed method in achieving performance improvement over offline-only baselines.
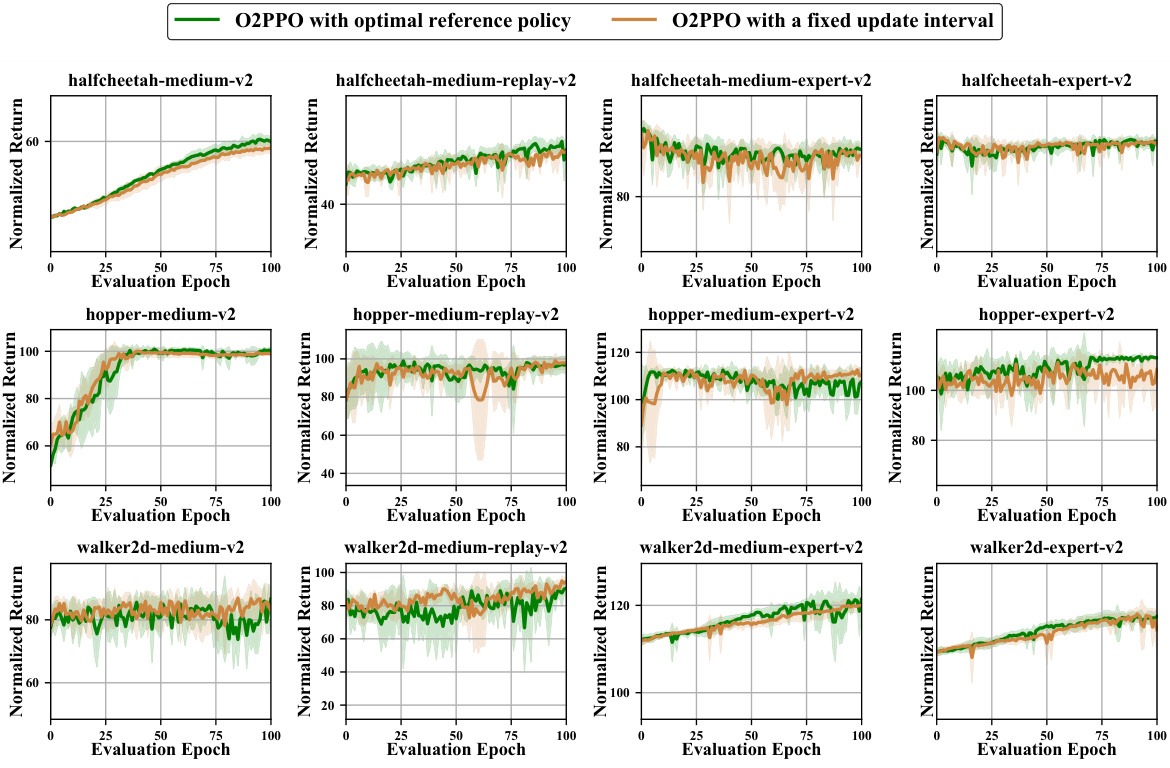
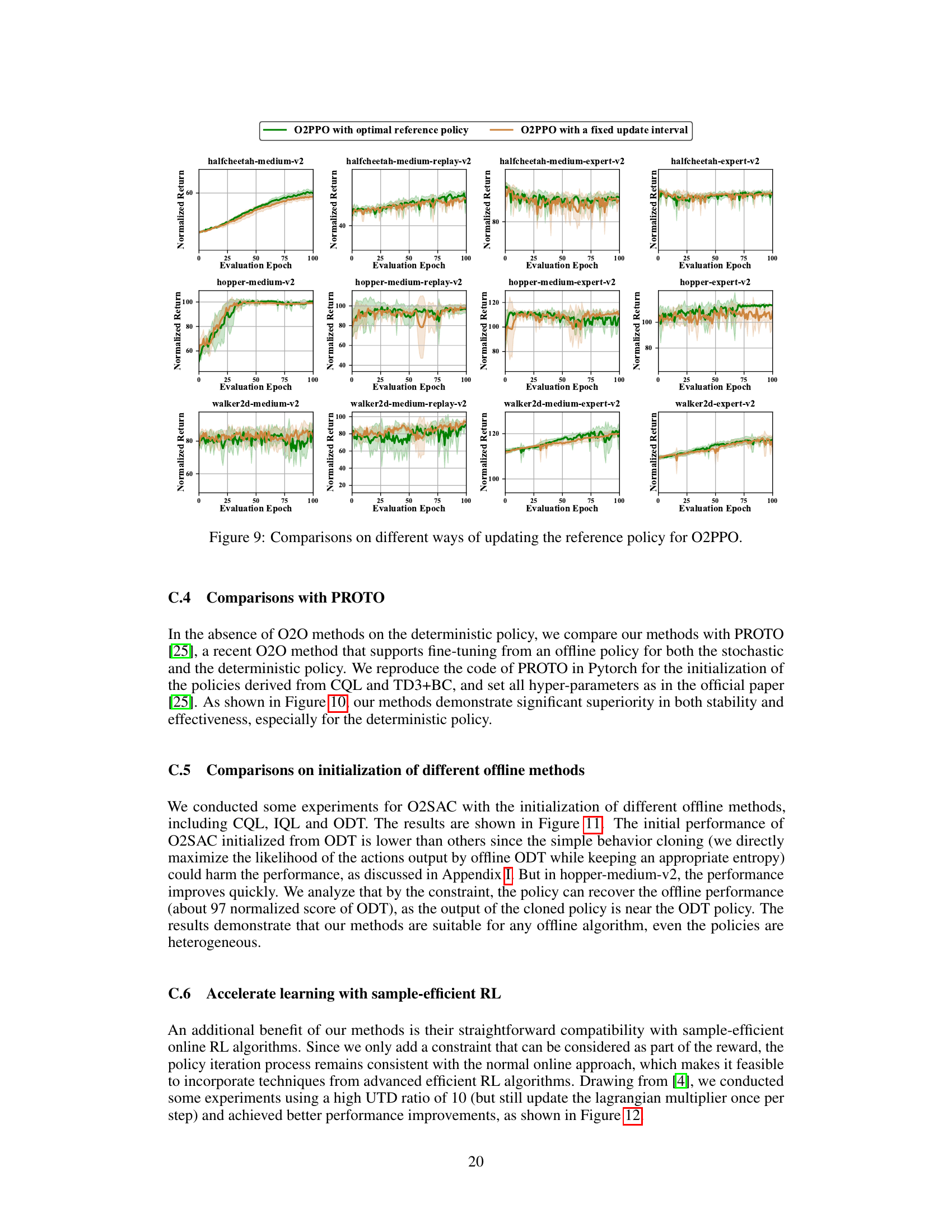
This figure compares the performance of O2SAC and O2TD3 algorithms when using two different methods for updating the reference policy during online fine-tuning. The first method uses the optimal historical policy, while the second uses a fixed update interval. The results are shown for various MuJoCo locomotion tasks. The shaded areas represent the standard deviation of multiple runs. This experiment highlights the impact of different reference policy update strategies on the stability and efficiency of online fine-tuning in offline-to-online reinforcement learning.

The figure presents the performance curves of various offline-to-online reinforcement learning (RL) methods on several MuJoCo locomotion tasks from the D4RL benchmark. It shows how the return (reward accumulated over time) of different algorithms changes during the online fine-tuning phase. The x-axis represents the number of evaluation epochs, and the y-axis represents the normalized return. Multiple lines represent different algorithms. The shaded area around each line shows the standard deviation. The purpose is to illustrate the comparative performance of different offline-to-online RL methods, highlighting their stability and efficiency in improving the online policy from a pre-trained offline policy.

This figure compares the online fine-tuning performance of the proposed O2SAC and O2TD3 methods with the PROTO and PROTO+TD3 methods on three MuJoCo locomotion tasks from the D4RL benchmark. The solid lines represent the average normalized return over five random seeds, and the shaded areas represent the standard deviation. The results show that O2SAC and O2TD3 achieve better or comparable performance than PROTO and PROTO+TD3, demonstrating their effectiveness in online fine-tuning of offline-trained policies.

This figure displays the performance curves of various offline-to-online reinforcement learning (RL) methods on several MuJoCo locomotion tasks from the D4RL benchmark. The x-axis represents the number of evaluation epochs during online fine-tuning, and the y-axis represents the normalized return achieved by each method. Different colors and shaded regions represent different methods and their standard deviations. The figure visually demonstrates the comparative performance of various methods, highlighting differences in stability and convergence during the online fine-tuning process.

This figure shows the performance of the policy during the value alignment process with different values of alpha (α). Alpha is a hyperparameter in the O2SAC algorithm that controls the strength of the value alignment. The figure shows that the performance of the policy improves as alpha increases, but the improvement is marginal after a certain point. This suggests that there is an optimal value of alpha for the value alignment process, and that using a value of alpha that is too high or too low can negatively impact the performance of the policy.

This figure shows the performance of evaluation and exploration scores during offline training using IQL. The evaluation score represents the average return when the policy selects actions based on the mean of the action distribution. The exploration score, conversely, uses actions sampled from the action distribution, reflecting the policy’s ability to explore various actions beyond the mean. The plot demonstrates the relationship between exploration and the overall normalized return during offline training, highlighting how much exploration is needed to reach a high return.
More on tables
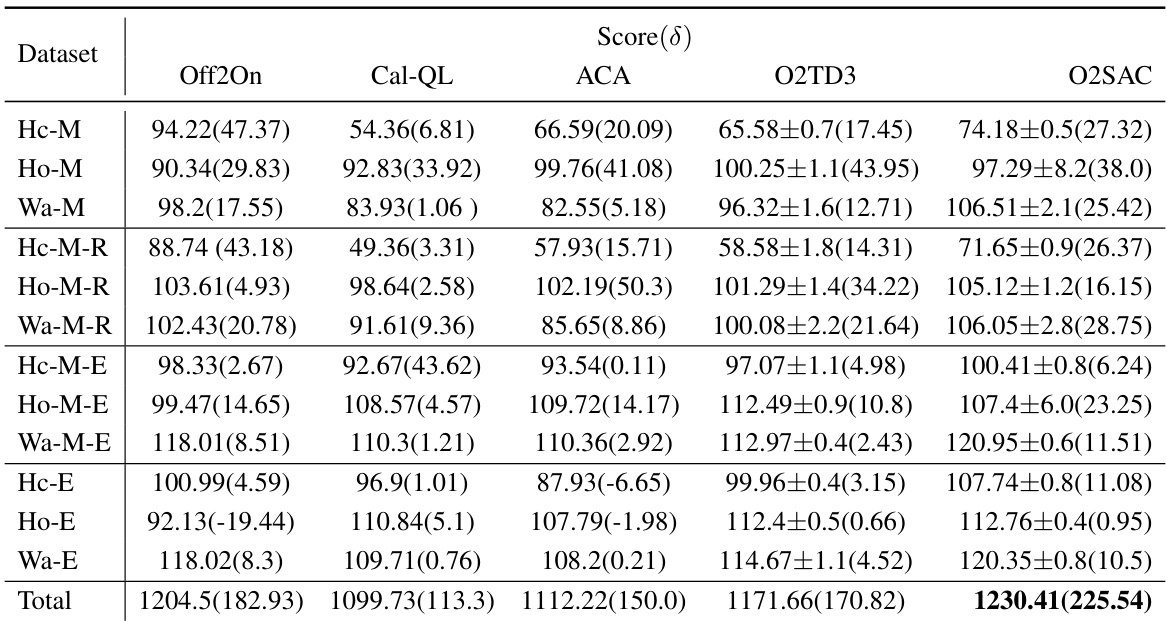
This table presents the average normalized D4RL scores achieved by various offline-to-online reinforcement learning (RL) methods on AntMaze navigation tasks. The scores are obtained after 200,000 interactions with the environment. The table compares the performance of the proposed methods (O2TD3, O2SAC, O2PPO) against several baseline methods (IQL, PEX, Cal-QL, ACA). The results are broken down by AntMaze environment variations (U-v2, U-D-v2) and provide a total score across all variations. The abbreviation ‘U’ stands for umaze and ‘D’ stands for diverse.

This table presents the average normalized D4RL scores achieved by different Offline-to-Online RL methods on AntMaze navigation tasks. The scores are obtained after 200,000 interactions with the environment. The table compares the proposed O2TD3, O2SAC, and O2PPO methods against several state-of-the-art baselines (IQL, PEX, Cal-QL, AWAC, and Off2On). The results are broken down by AntMaze environment variations (U-v2, U-D-v2), indicating the performance across different levels of task complexity. The ’total’ row sums the performance across all environments, providing an overall performance comparison of the methods.

This table presents the performance comparison between the offline policy (πoff) and the online policy (πon) after applying policy re-evaluation and value alignment. The results show the performance scores for different MuJoCo locomotion tasks, demonstrating the effectiveness of the proposed methods in improving policy performance from offline to online stages.

This table presents the average normalized D4RL scores achieved by various offline-to-online reinforcement learning (RL) methods on AntMaze navigation tasks. The methods compared include AWAC, IQL, PEX, O2SAC, and O2PPO. The table shows the performance ranges (min-max) obtained across different AntMaze environments (medium-play-v2, medium-diverse-v2, large-play-v2, large-diverse-v2) and provides the total scores across all environments. Finally, it shows the improvement (‘Δ’) in total score for each method compared to the baseline, indicating the effectiveness of the proposed methods in enhancing online RL performance.

This table presents the average normalized D4RL scores achieved by various offline-to-online reinforcement learning (RL) methods on AntMaze navigation tasks. The scores are calculated after 200,000 interactions with the environment. The table compares the proposed O2O methods (O2TD3, O2SAC, O2PPO) against existing baselines (IQL, PEX, Cal-QL, AWAC, ACA). The results are categorized by the type of AntMaze environment (umaze or diverse) to assess performance across different task complexities.

This table presents the average normalized D4RL scores achieved by various offline-to-online reinforcement learning (RL) methods on AntMaze navigation tasks. The scores are obtained after 200,000 interactions with the environment. The table compares the proposed methods (O2TD3, O2SAC, O2PPO) with several existing offline RL methods (IQL, PEX, Cal-QL, ACA). The results are broken down by dataset variant (U-v2, U-D-v2), and a total score is also provided. The abbreviations U and D refer to ‘umaze’ and ‘diverse’, respectively, indicating different variations of the AntMaze environment.
Full paper#