↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The ability of neural networks to learn useful features is a key advantage, yet it remains unclear how gradient-based training achieves this. Existing theories, like the Neural Tangent Kernel (NTK) regime, suggest that feature learning is limited in over-parameterized networks. This research addresses this gap by investigating feature learning mechanisms.
This paper employs local convergence analysis to demonstrate that gradient descent, under carefully designed regularization, can effectively learn ground-truth directions in later training stages. This challenges the NTK regime and provides stronger performance guarantees than existing kernel methods. The study combines both early-stage feature learning analysis with this local convergence analysis, offering a comprehensive view of how neural networks learn features throughout their training.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the prevailing Neural Tangent Kernel (NTK) theory, which limits the understanding of how neural networks learn features. By demonstrating feature learning in both early and late training stages, it opens new avenues for understanding neural network training dynamics and improving their performance.
Visual Insights#
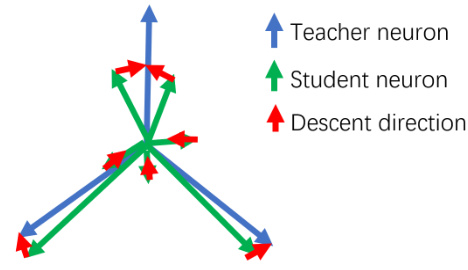
This figure illustrates the descent direction used in the proof. It shows how student neurons adjust toward the ground-truth directions of teacher neurons. Neurons close to the teacher neuron move towards it, while far-away neurons move towards zero. The arrows represent the descent direction, guiding the training towards optimal alignment.
In-depth insights#
Gradient Descent’s Feature Learning#
Gradient descent’s role in feature learning within neural networks is a complex and actively researched area. Early analyses, often relying on the neural tangent kernel (NTK) regime, suggested that feature learning was minimal, with network weights remaining close to their initial values. However, more recent work highlights feature learning’s emergence during the early stages of gradient-based training, indicating that initial weight updates are crucial in capturing relevant data features. This paper investigates an alternative mechanism, demonstrating that feature learning can also occur in later training stages, specifically through a local convergence process. By employing a carefully regularized objective function and analyzing gradient descent’s local convergence behavior, the authors prove that under certain conditions, the trained network will successfully capture ground-truth data directions. The interplay between early-stage and late-stage feature learning is also discussed, suggesting that a combination of both mechanisms contributes to successful feature extraction. This research challenges the traditional view of gradient descent, suggesting that its impact on feature learning is more nuanced and potent than initially believed.
Local Convergence Analysis#
A local convergence analysis in a machine learning context typically investigates the behavior of optimization algorithms within a small neighborhood of a solution. This focuses on proving that, given a sufficiently good initialization close enough to a true solution, the algorithm will converge to it. In the context of neural networks, such analysis might show how gradient descent refines an already reasonably accurate set of weights, demonstrating that feature learning isn’t only an early-stage phenomenon but can also happen during fine-tuning. This approach often relies on strong assumptions, such as a well-behaved loss landscape or particular structures of the target function, which might limit its generalizability to real-world scenarios. However, it provides crucial insights into the algorithm’s stability and convergence speed in its final stages. The analysis often involves advanced mathematical techniques, demonstrating strong theoretical guarantees that complement empirical observations and give a deeper understanding of the training dynamics.
Regularization’s Role#
Regularization plays a crucial role in training neural networks, particularly in preventing overfitting and improving generalization. Weight decay, a common form of regularization, adds a penalty term proportional to the magnitude of the weights, discouraging the network from learning excessively large weights. This helps to constrain the model’s complexity and prevent it from memorizing the training data. The paper likely explores how different regularization techniques affect the feature learning process, specifically in two-layer networks. Careful regularization can guide the optimization process, ensuring that the network learns the underlying structure of the data rather than just memorizing noise or irrelevant details. The choice of regularization strength is also important, as too much regularization can hinder the network’s ability to learn complex features, while too little regularization can lead to poor generalization. Local convergence analysis is used to examine the behavior of the network in the latter stages of training, and the balance between regularization and the learning capacity is likely investigated to see if regularization effects persist or are superseded at later stages. The findings are expected to demonstrate a deeper understanding of how regularization methods impact feature extraction and the overall performance of gradient-based training in neural networks.
Early-Stage Feature Learning#
Early-stage feature learning explores how neural networks learn meaningful representations during the initial phases of training. Research suggests that gradient descent, even in a few initial steps, can capture crucial information about the target function’s structure, often representing it within a low-dimensional subspace. This contrasts with the Neural Tangent Kernel (NTK) regime, which assumes feature learning is minimal. This early stage learning capability is particularly notable in 2-layer networks, where the first layer quickly learns a relevant subspace, enabling the subsequent layer to efficiently fit the target function. Several recent works highlight the effectiveness of this process for various target functions, including polynomials, single-index models, and sparse functions. However, understanding the precise mechanisms and limits of early-stage feature learning remains a crucial area of active research, as it opens up new possibilities for training more efficient and effective neural networks. Future research will likely focus on elucidating the interplay between early-stage feature learning and later stages of training, and also on developing more robust methods to leverage the advantages of this initial feature learning phase.
Limitations and Future Work#
A thoughtful analysis of the limitations section in a research paper should go beyond a simple listing of shortcomings. It requires a critical evaluation of the study’s scope and methodology, identifying potential weaknesses that might affect the validity, generalizability, or impact of the findings. This evaluation should delve into the assumptions made, highlighting their implications and exploring scenarios where these assumptions may not hold. A strong limitations section acknowledges the trade-offs made during the research process, acknowledging that the study may not cover all aspects of a complex problem. Specific limitations of the methodology should be mentioned, such as limitations related to data, sample size, experimental design, or analytical approaches. The discussion must also address the potential biases and their influence on the interpretations of the results, while acknowledging the generalizability issues associated with the study’s design and setting. Finally, a robust conclusion should propose concrete avenues for future research, expanding upon the current study’s findings and suggesting new directions to overcome existing limitations or address remaining questions. This forward-looking approach should suggest specific experiments or analyses that would enhance the overall research effort, offering a clear roadmap for future investigation.
More visual insights#
More on figures
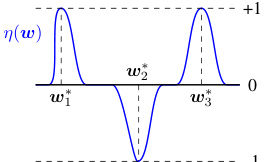
The figure shows a plot of the dual certificate η(w) as a function of w. The dual certificate is a function that is designed to be +1 around the ground-truth directions (w1 and w3) and -1 in between. It shows how the dual certificate, which measures the optimality of a solution, behaves sharply around the true parameters, decaying quadratically as it moves away from them. This property is crucial for the proof showing neurons concentrate around the ground truth directions.
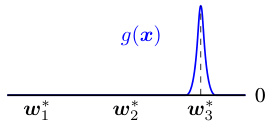
This figure illustrates the descent direction in the local convergence regime. The descent direction moves neuron wj toward either the ground-truth direction w or 0 depending on whether it is in the neighborhood of the teacher neuron w. Specifically, it moves far-away neurons towards 0 (setting qij = 0) and moves close-by neurons towards its closest minima qijw (the fraction of w that neuron wj should target to approximate).
Full paper#



















