↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Merging multiple predictive models for a target variable is a common problem in machine learning, particularly when models use different data. Existing methods typically ignore the causal relationships between variables. This can lead to inaccurate or suboptimal results, especially when some variables are unobserved. This paper directly addresses these challenges.
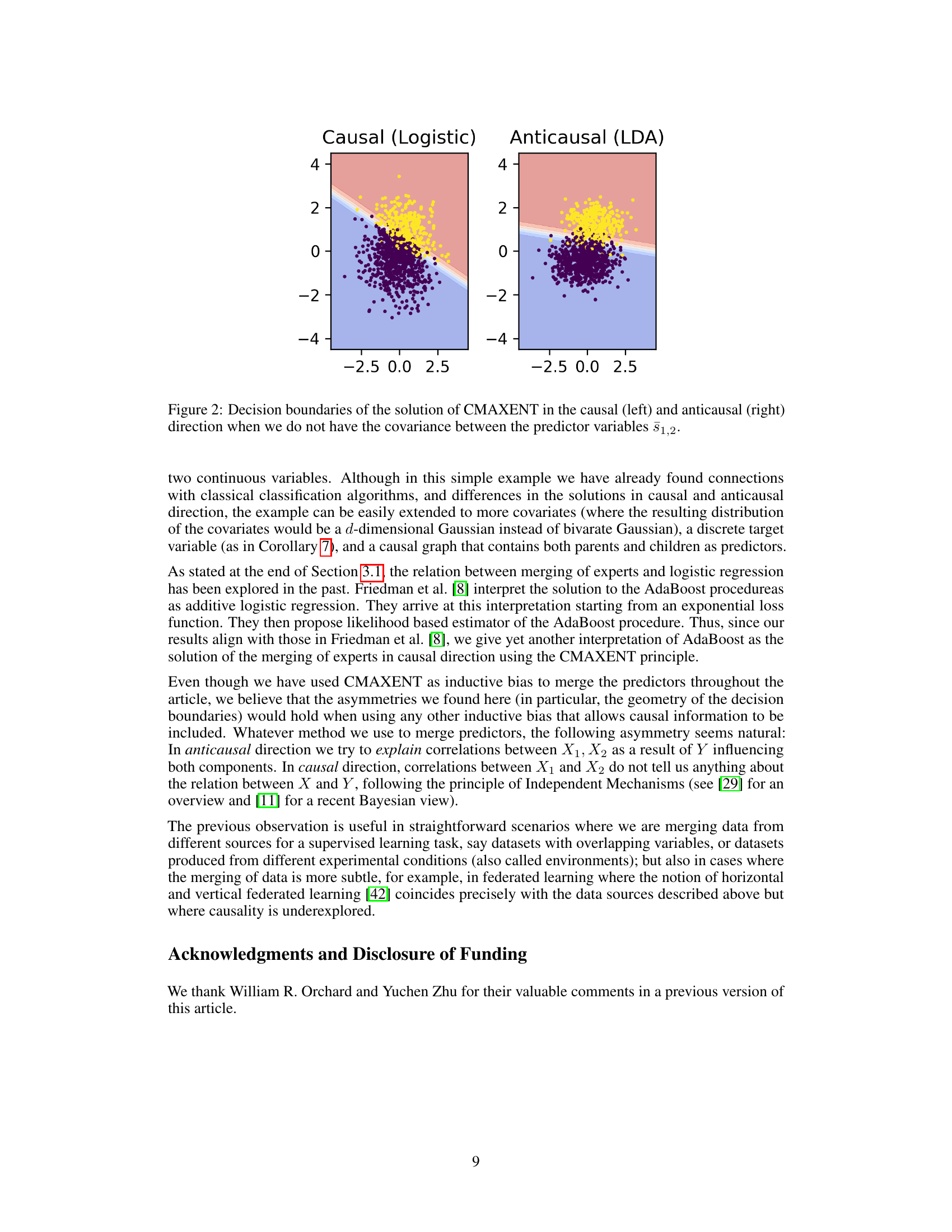
This work uses Causal Maximum Entropy (CMAXENT) to study the asymmetries that arise when merging predictors. When all data is observed, the method reduces to logistic regression for causal and Linear Discriminant Analysis for anticausal direction. However, when only partial data is available, the decision boundaries of these methods differ significantly, affecting out-of-variable generalization. The study provides a crucial advancement in understanding the impact of causality in predictive modeling.
Key Takeaways#
Why does it matter?#
This paper is crucial because it reveals how causal assumptions dramatically impact the merging of predictors, challenging existing methods that ignore causal direction. This has significant implications for model building and generalization, particularly in fields like medicine where causal relationships are paramount. The findings open new avenues for research in causal inference and improve machine learning model accuracy.
Visual Insights#

This figure shows two causal graphs representing different causal relationships between variables X1, X2, and Y. (a) depicts the causal direction where X1 and X2 are parents of Y (causes). (b) shows the anticausal direction where X1 and X2 are children of Y (effects). These graphs are fundamental to the study of causal vs. anticausal merging of predictors discussed in the paper. The asymmetry between these directions is the central theme of the paper.
Full paper#