Conformal Inverse Optimization

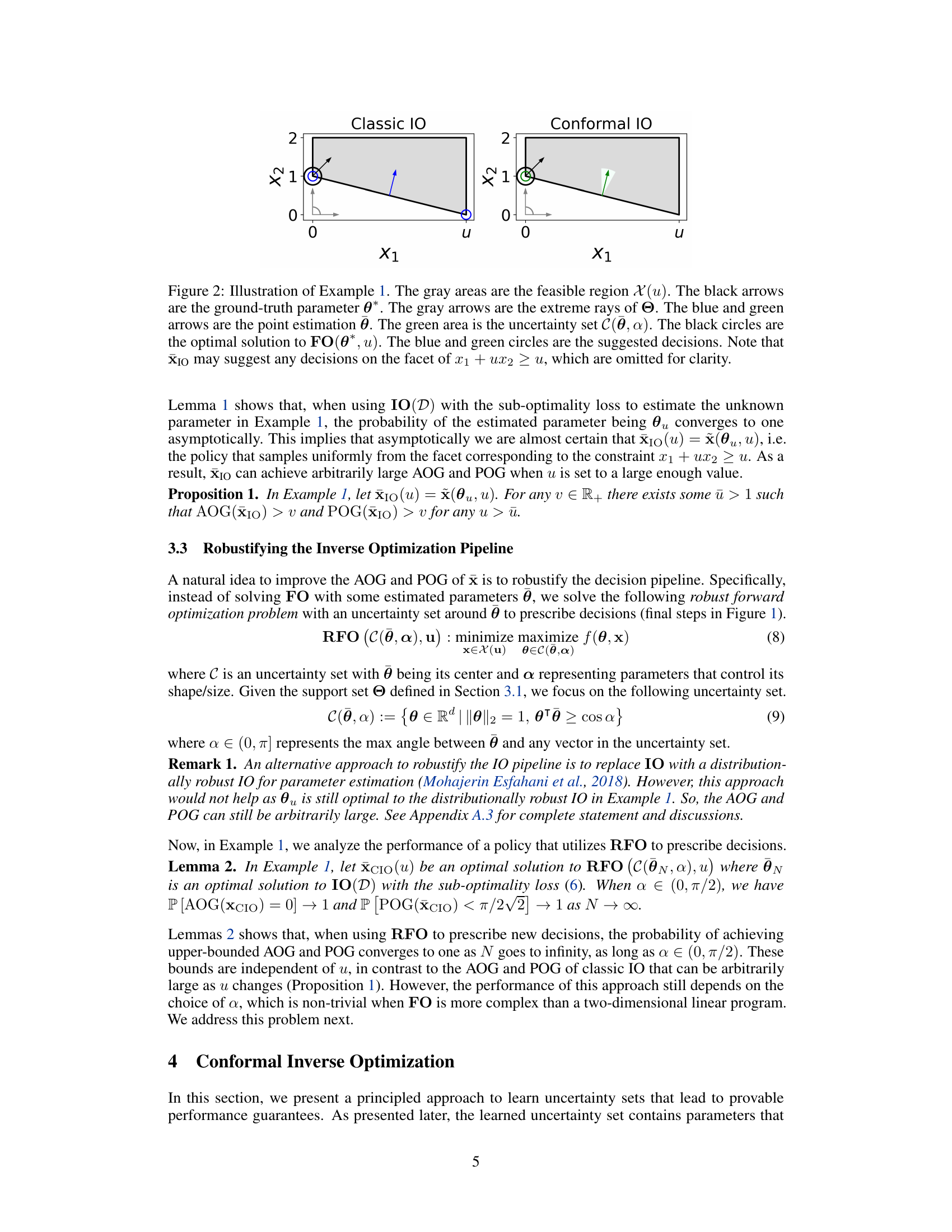
↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on inverse optimization and robust optimization because it introduces a novel framework, conformal inverse optimization, that enhances the quality and reliability of decisions made using these techniques. By addressing the issue of uncertainty in parameter estimation, this research contributes significantly to the fields of AI and decision-making. Furthermore, the provided theoretical guarantees and strong empirical performance make this work highly relevant to the broader community, opening exciting new avenues for future exploration, especially concerning the calibration of uncertainty sets and the application of conformal prediction in broader optimization settings.

Visual Insights

#

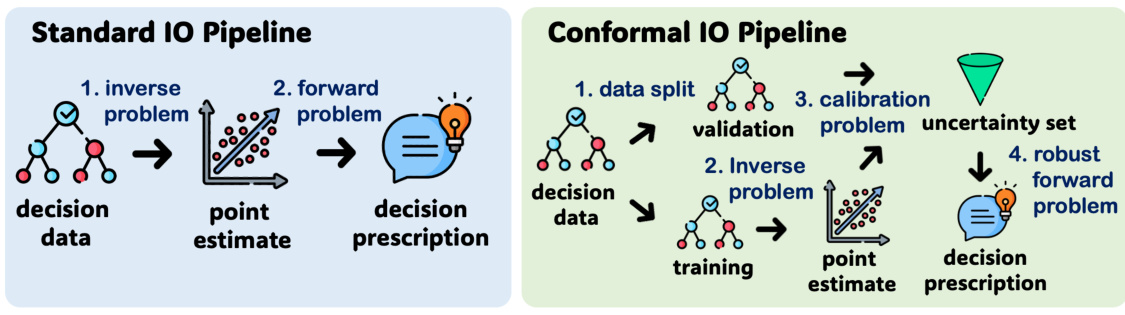
This figure compares the classic inverse optimization (IO) pipeline with the proposed conformal IO pipeline. The classic IO pipeline involves solving an inverse problem to estimate unknown parameters from decision data, followed by using those parameters to solve a forward optimization problem and prescribe new decisions. In contrast, the conformal IO pipeline first splits the data into training and validation sets. It then solves an inverse problem to estimate parameters, calibrates an uncertainty set using the validation data, and finally solves a robust optimization problem to generate decisions that are less sensitive to parameter uncertainty.

This table presents the performance of classic and conformal inverse optimization methods on Example 1, varying the parameter ‘u’. It shows the Actual Optimality Gap (AOG) and Perceived Optimality Gap (POG) for both methods, alongside theoretical bounds for the conformal IO method. The results illustrate how conformal IO significantly outperforms classic IO in terms of both AOG and POG, especially as ‘u’ increases.

In-depth insights

#

Conformal Inverse Opt

#

Conformal Inverse Optimization offers a novel approach to address limitations in traditional inverse optimization. Standard inverse optimization techniques often yield point estimates of parameters, leading to low-quality or counterintuitive decisions. Conformal Inverse Optimization improves on this by learning an uncertainty set around the parameters using conformal prediction, thus enabling a robust optimization model that produces more reliable and human-aligned prescriptions. The key strength lies in its provable guarantees on solution quality, using both ground-truth and perceived parameters, offering improved theoretical underpinning and practical value. Empirical results demonstrate stronger performance compared to classical methods, highlighting the effectiveness of the proposed framework in real-world applications. However, computational cost is a consideration, and future work could explore enhancements for efficiency.

Uncertainty Sets

#

The concept of ‘uncertainty sets’ is crucial in addressing the limitations of classic inverse optimization, particularly when dealing with real-world decision-making scenarios characterized by incomplete or noisy data and subjective human preferences. Uncertainty sets provide a robust mechanism to handle the inherent uncertainty associated with the unknown parameters in an optimization model. Instead of relying on a point estimate, which might be inaccurate, these sets consider a range of plausible parameter values. By formulating a robust optimization model that takes into account this uncertainty set, the approach aims to find solutions that are optimal across all possible scenarios, making them more reliable and less sensitive to estimation errors. The proposed method of learning uncertainty sets from decision data and incorporating them into a robust optimization model is a significant contribution, allowing for more reliable prescriptive decision-making in various applications where human preferences are involved.

Robust Optimization

#

Robust optimization is a powerful technique to address uncertainty in optimization problems. It focuses on finding solutions that remain feasible and near-optimal even when parameters deviate from their nominal values. This is achieved by explicitly modeling the uncertainty as a set (uncertainty set) and optimizing the objective function for the worst-case scenario within that set. The choice of uncertainty set is crucial, as it influences the conservatism and computational tractability of the resulting problem. Methods for constructing uncertainty sets from data are actively researched. Data-driven methods allow for learning the uncertainty set directly from observed decisions, making it more relevant to real-world applications, especially in inverse optimization problems where the true parameters are unknown. However, conservatism in these methods requires careful consideration to ensure that the resulting decisions remain practically useful and don’t become overly cautious, hence limiting their applicability.

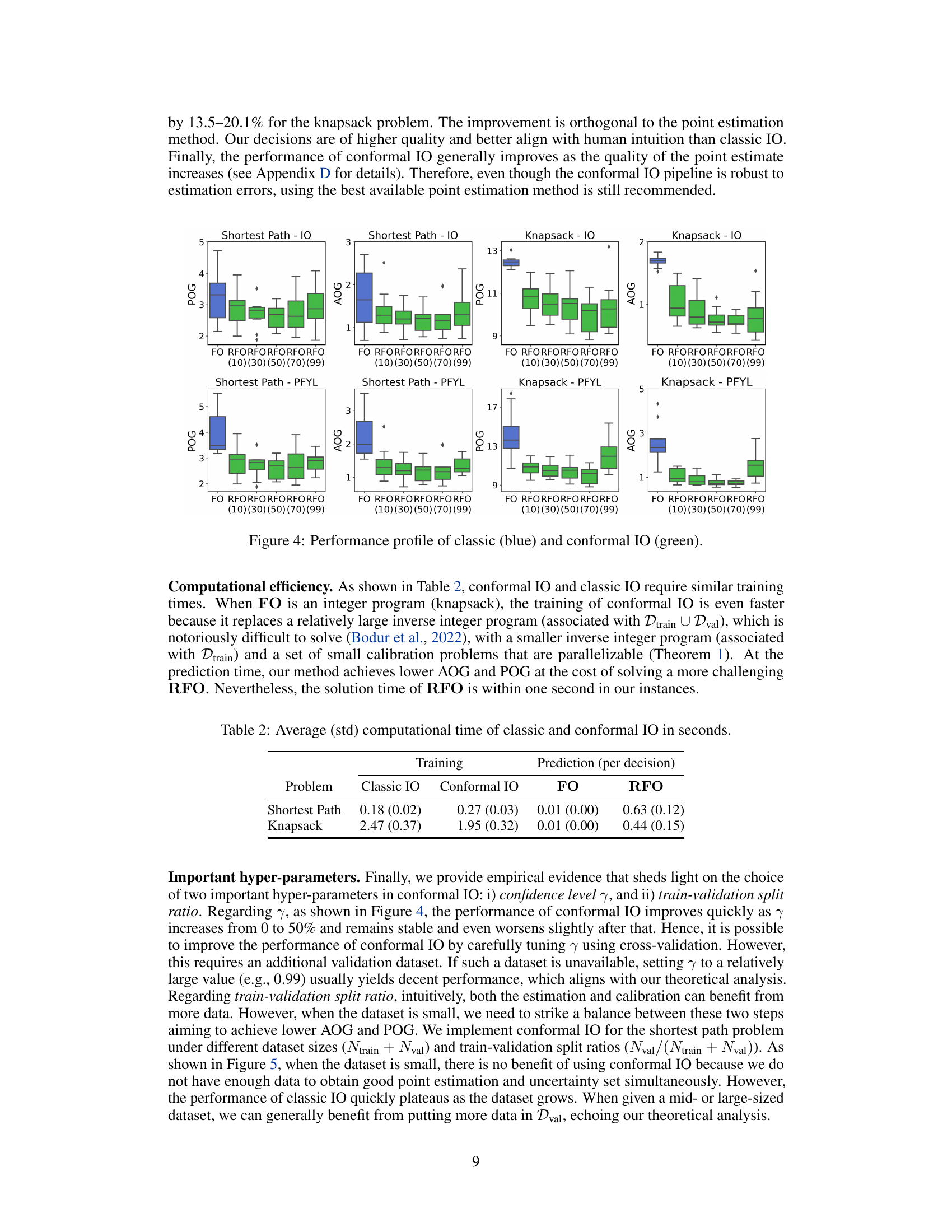
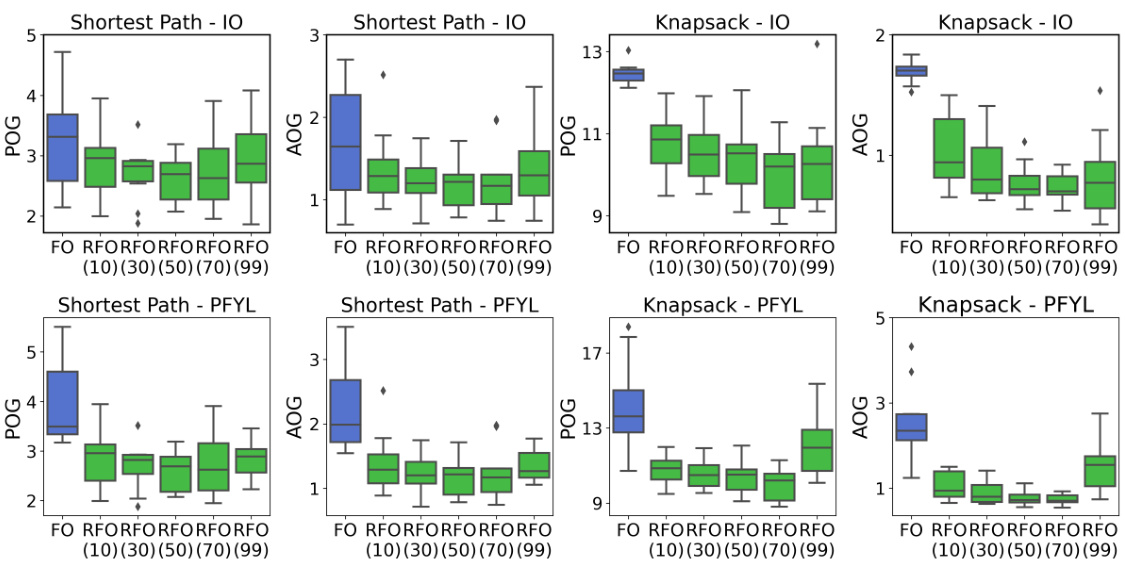
Empirical Analysis

#

An empirical analysis section in a research paper would typically present the results of experiments designed to test the hypotheses or claims made in the paper. A strong empirical analysis would begin by clearly describing the experimental setup, including the datasets used, the evaluation metrics, and any preprocessing steps. It’s crucial to ensure reproducibility by providing enough detail for others to replicate the experiments. The results would be presented clearly and concisely, often using tables, graphs, and other visualizations to aid comprehension. A thoughtful analysis would go beyond simply reporting the numbers; it would interpret the findings in light of the research questions, highlighting significant results and explaining any unexpected or counterintuitive observations. Crucially, it should acknowledge any limitations of the experimental design or data, and discuss the implications of the findings for the field. A robust empirical analysis might also include comparisons with existing methods or alternative approaches to demonstrate the novelty and impact of the research.

Future Directions

#

The research paper on conformal inverse optimization presents a promising new framework for decision-making, but several avenues for future work are apparent. Extending the approach to handle non-linear objective functions would significantly broaden its applicability. The current method’s reliance on linear objectives limits its use in complex real-world scenarios. Additionally, the computational cost of robust optimization could be addressed by exploring more efficient algorithms or approximations. Although the paper shows strong empirical performance, further investigation into the sensitivity of the method to hyperparameters is warranted to ensure robustness and reliable performance across diverse datasets and problem settings. Finally, exploring different methods for point estimation, potentially those directly optimizing downstream decision quality, could lead to further improvements. The development of theoretically grounded methods for selecting the confidence level (γ) in conformal prediction would also greatly enhance the practical utility of this approach.

More visual insights

#

More on figures

The figure visualizes the difference between classic and conformal inverse optimization pipelines. Classic IO involves obtaining a point estimation of unknown parameters and using it directly to prescribe decisions. Conformal IO differs by first learning an uncertainty set for the parameters and then solving a robust optimization model to recommend decisions, aiming for higher quality and alignment with human intuition.

This figure shows the empirical coverage achieved by the learned uncertainty set under different target coverage levels and sample sizes of the validation set. For both the shortest path and knapsack problems, the empirical coverage tends toward the target coverage as the validation sample size increases, demonstrating the asymptotic exactness property of the conformal inverse optimization approach. When the validation set is small (Nval = 10), the uncertainty set tends to over-cover (conservatively valid), while with larger validation sets (Nval ∈ {100, 200}) the coverage approaches the target level.

This figure compares the classic inverse optimization pipeline with the proposed conformal inverse optimization pipeline. The classic pipeline involves a point estimation of unknown parameters, followed by a direct decision prescription. In contrast, the conformal pipeline introduces uncertainty set learning and robust optimization for decision recommendation, leading to more robust and human-aligned decisions. This illustrates the core difference in their approaches to handling uncertainties and ensuring decision quality.

This figure shows the percentage reduction in Actual Optimality Gap (AOG) and Perceived Optimality Gap (POG) achieved by using conformal inverse optimization (IO) compared to classic IO. The results are shown across different percentages of the data used for validation (20%, 40%, 60%, 80%) and varying numbers of observed routes (160, 320, 480, 640, 800). The heatmap visualization makes it easy to see the impact of both the validation set size and the number of observed routes on the performance improvement.

More on tables

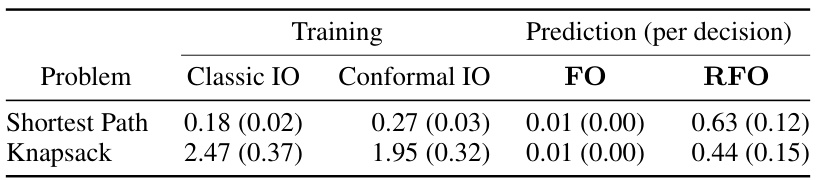
This table shows the average and standard deviation of the computational time in seconds for both training and prediction phases of the Classic IO and Conformal IO methods. The training time is for the entire dataset, while the prediction time is reported per decision. The table breaks down the timing for both the forward optimization problem (FO) and the robust forward optimization problem (RFO) for the Conformal IO method. It gives a comparison of computational costs between the two approaches for different problem types (shortest path and knapsack).

This table shows the mean and standard deviation of the actual optimality gap (AOG) and the perceived optimality gap (POG) achieved by the conformal inverse optimization method across different levels of point estimate quality. The point estimate quality is represented by the angular deviation (δ) from the ground truth parameter. As can be seen from the table, the performance of the conformal IO method degrades as the point estimate quality worsens (i.e., as δ increases).

Full paper

#