↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Self-supervised learning (SSL) excels at extracting representations from unlabeled data, but suffers from dimensional collapse, where a few eigenvalues dominate the feature space, hindering performance. Existing solutions primarily focused on representation collapse, neglecting the impact on weight matrices and hidden features. This limited the effectiveness of existing methods.
This paper introduces orthogonal regularization (OR) to mitigate dimensional collapse by promoting orthogonality within the encoder’s weight matrices. Empirical results demonstrate that OR consistently boosts performance across diverse SSL methods and network architectures (CNNs and Transformers). The method shows a consistent gain across various benchmark datasets, highlighting its broad applicability and robustness. The approach is theoretically sound and easy to implement, making it a valuable contribution to the SSL field.
Key Takeaways#
Why does it matter?#
This paper is crucial for self-supervised learning (SSL) researchers as it directly addresses the prevalent issue of dimensional collapse. By introducing orthogonal regularization, it offers a novel, effective solution to enhance SSL performance across various architectures. This opens new avenues for improving SSL model robustness and generalizability, impacting numerous downstream applications.
Visual Insights#

This figure illustrates the concept of dimensional collapse in self-supervised learning (SSL). It shows how dimensional collapse can occur in three places within the encoder: the weight matrices (W1, W2), the hidden features, and the final representations. It also compares existing methods, which act only on the representations, with the proposed orthogonality regularization method, which acts directly on weight matrices and has theoretical guarantees on preventing collapse.

This table presents a comparison of the performance of the BYOL self-supervised learning method with and without two different techniques: feature whitening from the VICREG method and Soft Orthogonality (SO). The results are shown in terms of Top-1 and Top-5 accuracy on the CIFAR-10 dataset. The table demonstrates the effect of each technique on the overall accuracy of the BYOL method.
In-depth insights#
SSL Dimensional Collapse#
Self-Supervised Learning (SSL) has witnessed remarkable progress, yet dimensional collapse, where representations are confined to a low-dimensional subspace, remains a significant hurdle. This phenomenon arises from the dominance of a few large eigenvalues in the eigenspace of feature representations and weight matrices within the encoder network. In essence, the network fails to learn diverse, informative features, resulting in representations that lack expressiveness and generalization capabilities. This collapse manifests in various ways: weight matrices become redundant, limiting their ability to extract meaningful information; hidden features lack diversity, impeding the network’s ability to model complex data distributions; and representations become less discriminative, reducing downstream task performance. Addressing dimensional collapse is crucial for unlocking the full potential of SSL, prompting research into innovative regularization techniques and architectural modifications that promote richer, more expressive feature learning.
Orthogonal Regularization#
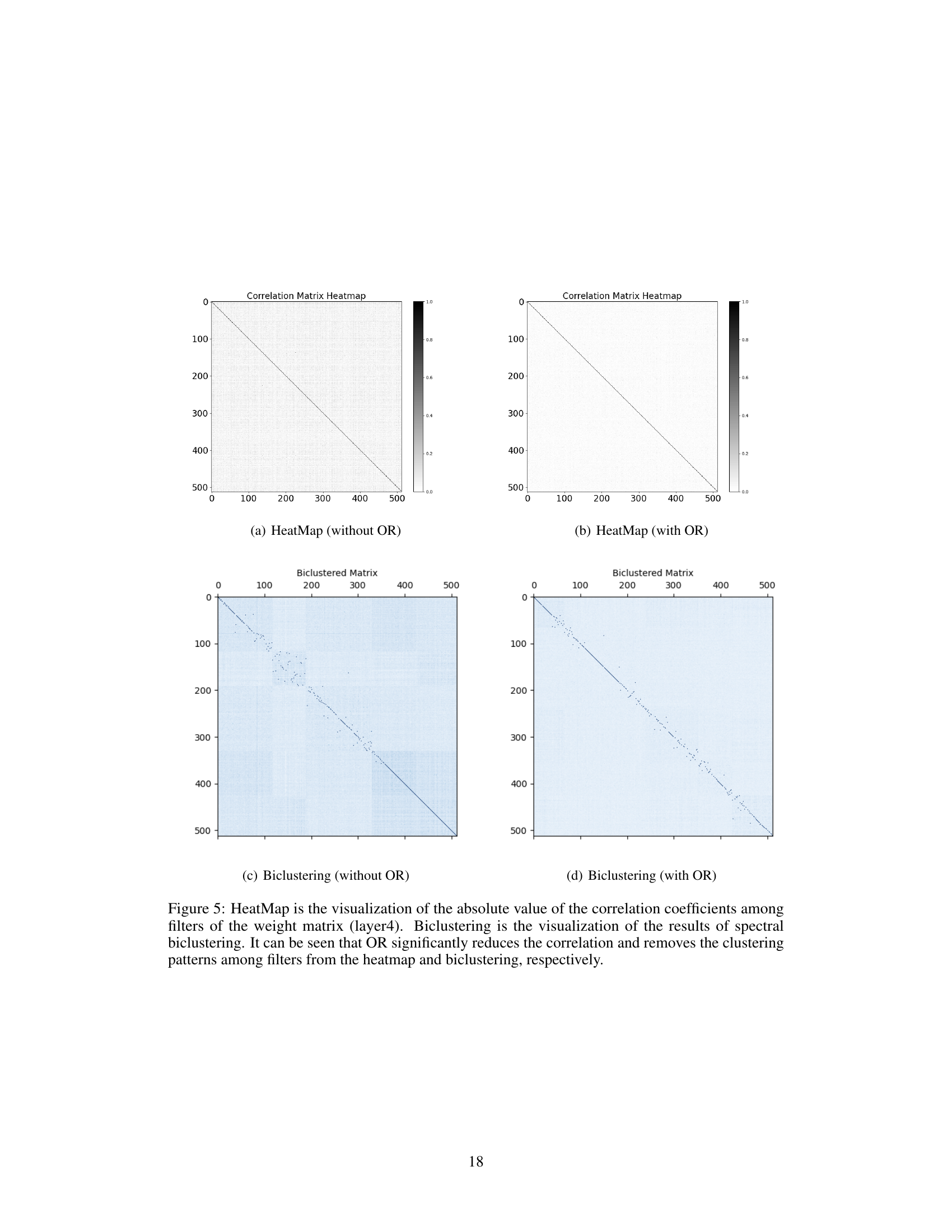
Orthogonal regularization, in the context of self-supervised learning, is a technique aimed at mitigating the problem of dimensional collapse. Dimensional collapse occurs when a neural network’s learned representations are concentrated in a small subspace of the feature space, hindering its ability to capture the full complexity of the data. This is often observed as a few dominant eigenvalues in the eigendecomposition of feature covariance matrices. The core idea of orthogonal regularization is to impose constraints on the weight matrices of the network to encourage orthogonality among the learned filters or features. This promotes a more diverse and evenly distributed representation, preventing the domination of a few features and potentially alleviating dimensional collapse. The method’s effectiveness stems from the theoretical property that orthogonal weight matrices help ensure filters are less correlated, leading to richer and more informative feature representations. Various techniques, such as soft orthogonality and spectral restricted isometry property regularization, can be employed to achieve this orthogonality, which can be integrated during the model pretraining phase. Importantly, experimental evaluations demonstrate improvements in the performance of self-supervised learning models on various benchmark datasets when using orthogonal regularization, highlighting its value as a regularizer to improve the quality of learned representations and model robustness.
SSL Benchmark Enhancements#
The heading “SSL Benchmark Enhancements” suggests a focus on improving the performance of self-supervised learning (SSL) methods across various benchmark datasets. A thoughtful analysis would consider the specific SSL methods evaluated, the types of benchmark datasets used (e.g., image classification, object detection), and the metrics used to quantify enhancement (e.g., accuracy, precision, recall). The in-depth exploration should then examine the nature of the improvements: did the enhancements arise from novel architectures, improved training strategies, or perhaps a combination? Understanding the scope of the enhancements is key—were they consistent across different datasets and architectures, or were improvements limited to specific scenarios? Finally, a critical evaluation would assess the significance of the enhancements; were they marginal or substantial, and do they push the state-of-the-art in SSL? A robust analysis would also investigate potential limitations, such as computational cost or increased complexity of the improved methods.
Broader SSL Implications#
The potential broader implications of this research on self-supervised learning (SSL) are significant. Orthogonal Regularization (OR), by mitigating dimensional collapse, could unlock substantial improvements in various SSL methods, particularly those susceptible to this phenomenon. This may lead to better performance across diverse benchmarks and architectures, impacting the efficacy of both contrastive and non-contrastive approaches. The consistent gains observed across multiple backbones suggest a robust and generalizable approach. Further research should explore OR’s effectiveness on larger-scale datasets and diverse architectures, including Transformers and generative models. This work provides a valuable foundation for advancing the field of SSL, potentially improving downstream tasks and even influencing the development of novel SSL techniques. Moreover, the ease of integration with existing SSL methods makes OR a practical tool for researchers, offering a promising direction for enhancement without significant architectural modifications.
Future Research#
The paper’s exploration of orthogonal regularization (OR) in self-supervised learning (SSL) opens exciting avenues for future research. Extending OR’s application to other foundation models, such as vision generative models (e.g., MAE), autoregressive models (like GPTs and LLAMAs), and contrastive language-image pre-training models, is crucial. This would allow for a more comprehensive understanding of OR’s effectiveness across different architectures and data modalities. Furthermore, a deeper theoretical analysis could provide a stronger foundation for OR’s efficacy in preventing dimensional collapse, potentially leading to improved performance and stability in SSL. Investigating how OR interacts with other regularization techniques would also be valuable, as it might enhance performance further. Finally, exploring OR’s robustness in various scenarios, such as handling noisy data, varying data distributions, and different training strategies, is vital for establishing its practical applicability and wider adoption within the field.
More visual insights#
More on figures

This figure illustrates how dimensional collapse can occur in self-supervised learning (SSL) models. It shows an encoder with two blocks, each containing a linear layer and activation function. Dimensional collapse can happen at various points: within the weight matrices (W1, W2), the hidden features, and the final representations. Existing approaches focus on modifying the representations, lacking a theoretical guarantee that it would fix the issue in the weight matrices and hidden features. In contrast, this paper’s approach directly constrains the weight matrices, ensuring orthogonality, which theoretically prevents collapse across all three areas.

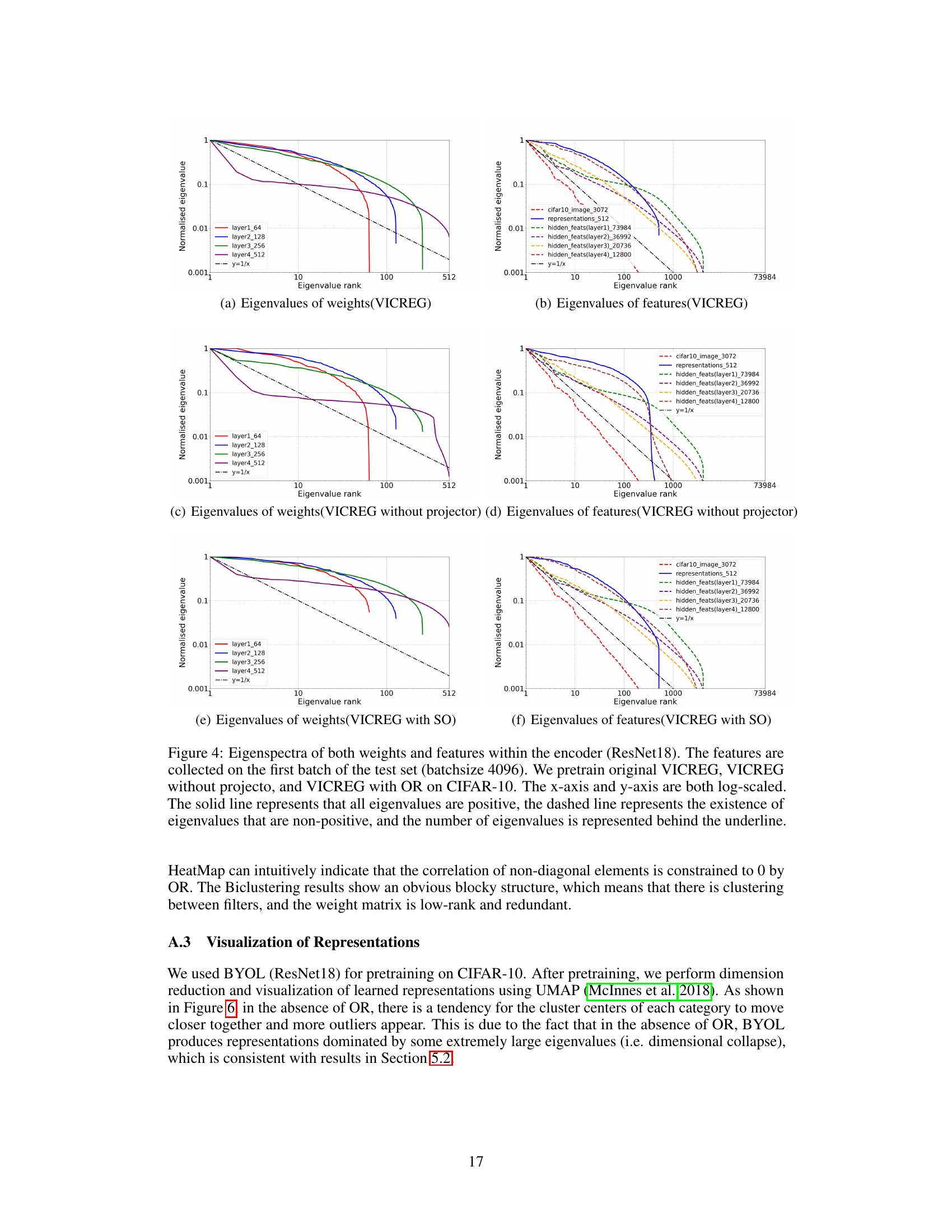
This figure displays the eigenvalue distribution of both weight matrices and features within a ResNet18 encoder for three BYOL training scenarios: without orthogonality regularization (OR), with VICREG’s feature whitening, and with OR. The plots show how OR helps prevent eigenvalues from decaying rapidly, indicating a more even distribution of information across the feature space and suggesting a reduction in dimensional collapse. This contrasts with the rapid decay observed in the other scenarios.
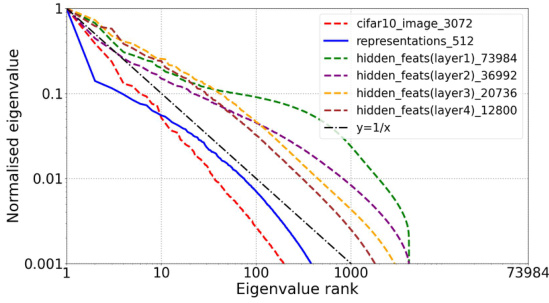
This figure displays the eigenvalue distribution of both weight matrices and features (input features, hidden features, and representations) within a ResNet18 encoder, comparing three BYOL training scenarios: without orthogonality regularization (OR), with feature whitening (from VICREG), and with OR. The plots reveal that OR effectively mitigates the dimensional collapse issue, resulting in more uniform eigenvalue distributions.

This figure compares the eigenvalue distributions of weight matrices and features (input, hidden, and representations) within a ResNet18 encoder, trained with three different methods: BYOL without orthogonality regularization (OR), BYOL with VICREG’s feature whitening, and BYOL with OR. The plots show how the eigenvalue decay rate changes across different layers and methods, illustrating the impact of OR in preventing dimensional collapse.
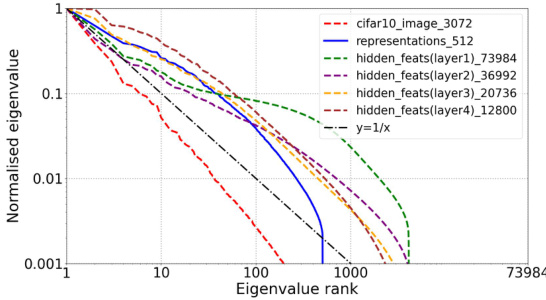
This figure visualizes the eigenvalue distribution of weight matrices and features (input, hidden, and representation) within the ResNet18 encoder of a BYOL model trained on CIFAR-10 under three conditions: without orthogonal regularization (OR), with feature whitening from VICREG, and with OR. The plots show how the eigenvalues decay across different ranks, indicating the extent of dimensional collapse. A slower decay suggests a more uniform distribution of information across feature dimensions, whereas a rapid decay signifies dimensional collapse where a few dimensions dominate. The figure aims to demonstrate OR’s effectiveness in mitigating dimensional collapse in both weight matrices and features.

This figure displays the eigenvalue distribution of both weight matrices and feature maps within the ResNet18 encoder of a BYOL model trained on CIFAR-10. Three training scenarios are compared: without orthogonal regularization (OR), with feature whitening from VICREG, and with OR. The plots show that OR leads to a more uniform eigenvalue distribution, indicating a reduction in dimensional collapse.

This figure visualizes the eigenvalue distributions of both weight matrices and features (input features, hidden features, and representations) within a ResNet18 encoder pretrained using BYOL on CIFAR-10. Three different scenarios are shown: BYOL without orthogonal regularization (OR), BYOL with feature whitening (from VICREG), and BYOL with OR. The plots show that OR effectively prevents dimensional collapse, evidenced by the slower decay of eigenvalues and fewer negative values, indicating a more uniform distribution of information across dimensions compared to other methods.

This figure illustrates how dimensional collapse can affect different parts of a self-supervised learning (SSL) model. It shows that existing methods primarily focus on addressing collapse in the final representations, leaving the weight matrices and hidden features potentially uncontrolled. In contrast, the proposed method directly addresses collapse in the weight matrices, which indirectly helps control collapse in hidden features and representations.
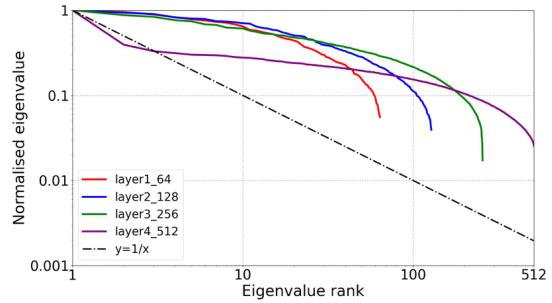
This figure visualizes the eigenvalue distribution of weight matrices and features (input features, hidden features, and representations) within a ResNet18 encoder using BYOL pre-training. Three scenarios are compared: BYOL without orthogonality regularization (OR), BYOL with feature whitening (from VICREG), and BYOL with OR. The plots show how OR affects eigenvalue distribution, indicating improved feature diversity and reduced dimensional collapse.
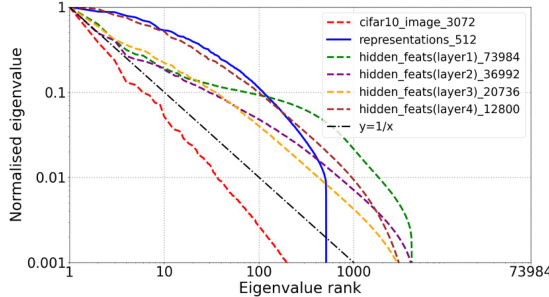
This figure visualizes the eigenvalue distributions of both weight matrices and features (input, hidden, and representation) within a ResNet18 encoder when using BYOL for pre-training on CIFAR-10, with and without Orthogonal Regularization (OR) and with VICREG’s feature whitening. The plots show how OR and feature whitening techniques impact the eigenspectra, indicating the presence or absence of dimensional collapse in different model components.

This figure illustrates the concept of dimensional collapse in self-supervised learning (SSL). It shows how the encoder, consisting of multiple blocks with linear or convolutional layers, can lead to collapse in three different places: the weight matrices (W1, W2), hidden features, and the final representations. Existing approaches primarily focus on fixing issues with the representations, but this figure argues that this indirect approach lacks theoretical guarantees. Their method aims to directly regularize the weight matrices, providing theoretical guarantees of preventing collapse in the weight matrices and indirectly improving hidden features and representations.
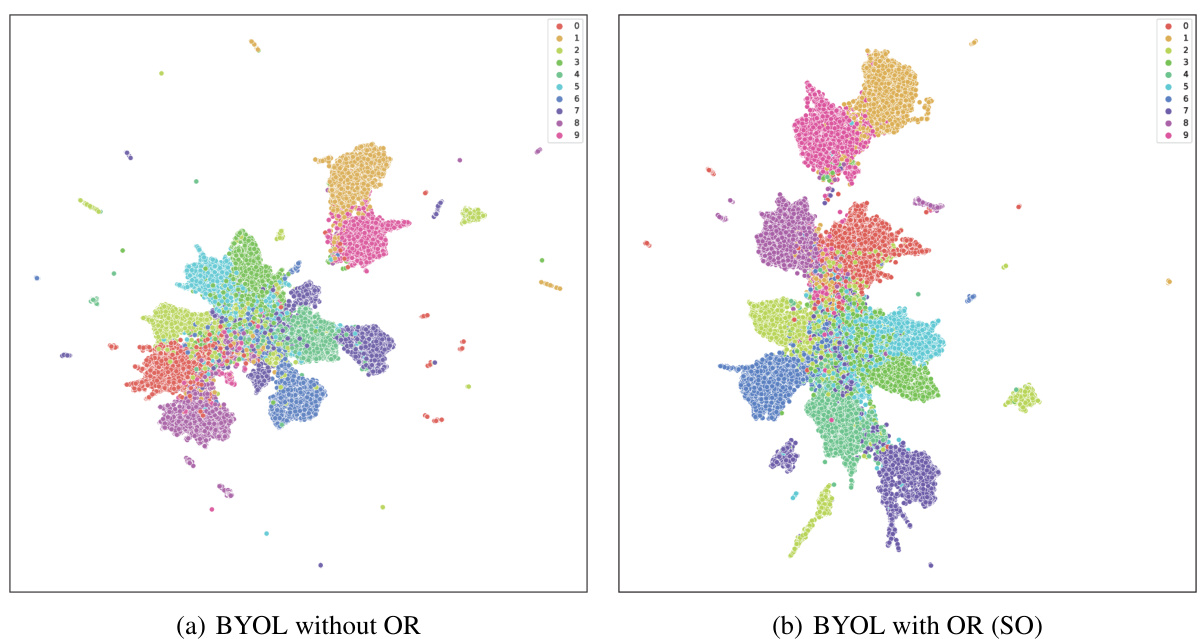
This figure visualizes the learned representations from BYOL with and without orthogonal regularization (OR). It uses UMAP for dimensionality reduction to project the high-dimensional representations into a 2D space for visualization. Each point represents a data sample, and the color indicates its class label. The plots show that the BYOL model without OR shows more cluster overlap and scattered points, indicating dimensional collapse (where data points are mapped to a limited number of dimensions). Conversely, BYOL with OR has more clearly separated clusters of data points, demonstrating its effectiveness in preventing dimensional collapse and preserving more of the data’s inherent structure.
More on tables
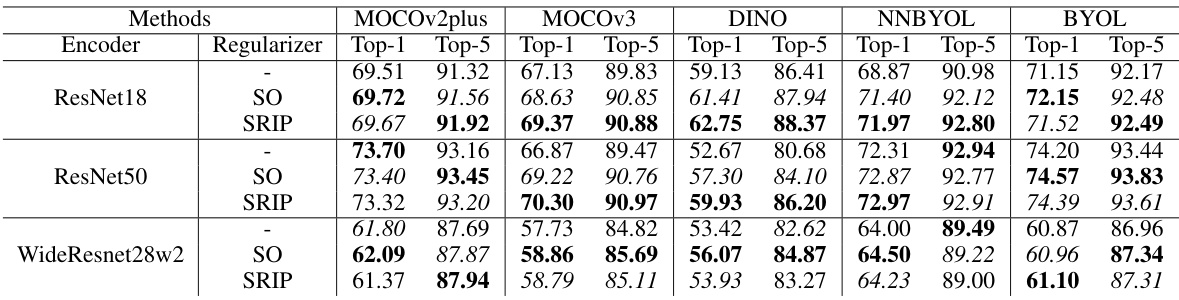
This table presents the Top-1 and Top-5 classification accuracy results on CIFAR-100 using various CNN backbones and 13 SSL methods. The results are shown for both the original SSL methods and those modified with Orthogonality Regularization (OR) using either Soft Orthogonality (SO) or Spectral Restricted Isometry Property Regularization (SRIP). The best and second-best results for each model/backbone are highlighted.

This table presents the classification accuracy results on the CIFAR-100 dataset using the DINO (in Solo-learn) self-supervised learning method. The results are broken down by the type of Vision Transformer (ViT) encoder used (VIT-tiny, VIT-small, VIT-base) and whether or not Orthogonal Regularization (OR) was applied during training. The ‘Top-1’ and ‘Top-5’ columns indicate the accuracy of the top-1 and top-5 predictions, respectively.
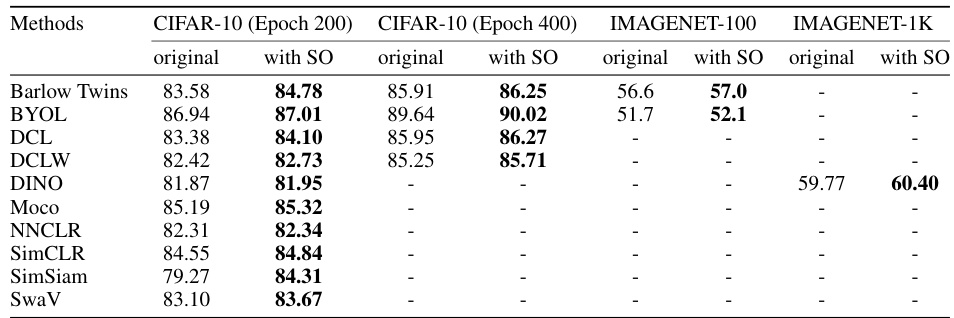
This table presents the performance of 13 self-supervised learning (SSL) methods on four different datasets (CIFAR-10, CIFAR-100, IMAGENET-100, and IMAGENET-1K) using two different backbones: ResNet18 and ResNet50. The results show the performance of both the original SSL methods and those with the addition of Soft Orthogonality (SO) as a regularizer. The table highlights the impact of the proposed orthogonality regularization technique on the performance of various SSL methods across different datasets and backbones.

This table compares the performance of three different BYOL models trained on CIFAR-10: a baseline BYOL model, a BYOL model with Soft Orthogonality (SO) regularization, and a BYOL model using the feature whitening technique from the VICREG method. The results are reported as Top-1 and Top-5 accuracies, showcasing the impact of different regularization methods on the model’s performance. The table highlights how SO regularization, in contrast to the feature whitening technique, leads to improved results.

This table presents the classification accuracy achieved on various transfer learning datasets after pre-training with different methods (BYOL with and without Orthogonality Regularization). It demonstrates the generalization capability of the models trained with orthogonality regularization, showcasing improved performance across a range of downstream tasks.

This table compares the performance of BYOL with and without Orthogonality Regularization (OR) on the ImageNet-1k dataset. The model used is ResNet50, trained for 100 epochs with a batch size of 128. The results show the Top-1 and Top-5 accuracy for image classification and Average Precision (AP) metrics for object detection on the validation set. The best performing model in each category is highlighted in bold.

This table compares the top-1 and top-5 accuracies of three different BYOL models trained on CIFAR-10: the original BYOL model, BYOL with soft orthogonality (SO) regularization, and BYOL with the feature whitening technique from VICREG. It demonstrates the impact of different regularization techniques on model performance, specifically highlighting the effectiveness of SO compared to feature whitening.
This table compares the top-1 and top-5 accuracy of the BYOL model on CIFAR-10 dataset with and without using the feature whitening technique from VICREG and Soft Orthogonality (SO). It demonstrates the effect of each technique on improving the model’s performance.

This table compares the top-1 and top-5 classification accuracy of the BYOL model on the CIFAR-10 dataset using three different methods: the original BYOL model, BYOL with soft orthogonality (SO) regularization, and BYOL with the feature whitening technique from the VICREG model. The results show that both SO regularization and the feature whitening technique improve the accuracy compared to the original BYOL model.
Full paper#