A Simple yet Universal Framework for Depth Completion

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it addresses a critical challenge in computer vision: consistent depth estimation across diverse scenes and sensors. It introduces a novel Universal Depth Completion (UniDC) problem and proposes a simple yet effective solution using minimal labeled data. This is highly relevant to real-world applications of machine learning, where acquiring extensive labeled data is often infeasible. Furthermore, the use of hyperbolic embedding opens up new avenues for handling hierarchical structures in 3D data, which has broader implications beyond depth completion.

Visual Insights

#

This figure compares three different approaches to depth completion: (a) Conventional SPNs which use an encoder-decoder to produce dense depth maps from sparse depth input and RGB image, (b) DepthPrompting (CVPR24), which leverages a pre-trained foundation model to generate a relative-scale initial depth map and then use Euclidean affinity and a refinement process to obtain the final dense depth map. (c) The proposed method, which utilizes a foundation model to extract depth-aware features and then performs a hyperbolic sparse-to-dense conversion to generate the initial depth, before using a hyperbolic refinement process to obtain the final depth map. The key difference is the use of hyperbolic geometry in the proposed method to capture the hierarchical structure of 3D data, leading to improved adaptability and generalization.

This table presents a quantitative comparison of different depth completion methods on the NYUv2 dataset. It compares performance across various experimental settings: 1-shot, 10-shot, 100-shot learning, and 1-sequence training. The metrics used for comparison are RMSE, MAE, and DELTA1 (inlier ratio), providing a comprehensive evaluation of each method’s accuracy and robustness in low-data and limited-training scenarios.

In-depth insights

#

UniDC Problem Defined

#

The UniDC (Universal Depth Completion) problem, as defined in the research paper, centers on the challenge of achieving consistent and accurate depth estimation across diverse scenes and sensor types. This is a significant departure from existing methods that often rely on extensive, pixel-wise labeled data and struggle with sensor-specific biases. UniDC highlights the need for a generalizable approach that can handle a wide variety of scenarios and sensors with minimal labeled data. The core challenge lies in creating generalizable knowledge about 3D scene structure that is applicable across different sensor modalities and scene configurations. This demands a robust adaptation mechanism capable of handling varied sensor specifications and quickly adjusting to new unseen environments. The paper acknowledges the high annotation costs associated with traditional depth estimation approaches which further motivates the pursuit of a solution that leverages minimal labeled data and exploits transferable knowledge from foundational models to achieve superior generalization.

Foundation Model Use

#

The effective utilization of foundation models is a crucial aspect of the research. The authors highlight the advantages of leveraging pre-trained knowledge from a monocular depth estimation model, arguing that it provides a comprehensive understanding of 3D structures, reducing the need for extensive training on new data. This approach not only improves efficiency and reduces the cost of data acquisition but also enhances the generalization capabilities of the model to unseen sensor configurations and environments. However, a direct integration of a foundation model is not without challenges. The paper acknowledges the potential issues related to scale variance across different depth sensors and the difficulties in achieving generalizability with minimal labeled data. Addressing these challenges forms a key contribution of the study. The use of hyperbolic embedding emerges as a compelling solution, improving model adaptability and robustness by capturing the implicit hierarchical structure of 3D data. This innovative strategy enables the model to handle a wider variety of sensors and scenarios more effectively. Therefore, the thoughtful integration of a foundation model, coupled with advanced techniques like hyperbolic embedding, constitutes a critical advancement in the field of depth completion.

Hyperbolic Geometry

#

The application of hyperbolic geometry in this research is intriguing. Hyperbolic space’s inherent hierarchical structure is leveraged to improve the representation of 3D data, particularly in handling the complexities of depth estimation from sparse sensor inputs. This approach offers a compelling alternative to traditional Euclidean methods, mitigating challenges associated with bleeding errors and scale variance across different depth sensors. By embedding features into hyperbolic space, the model implicitly captures hierarchical relationships within the data, enhancing adaptability and generalization capabilities. The use of multi-curvature hyperbolic spaces further augments the model’s flexibility, allowing for dynamic adaptation to diverse scenes and sensor configurations. The results suggest that hyperbolic geometry provides a significant improvement in the accuracy and robustness of depth completion, particularly in low-data scenarios. This is a promising area of research with potential implications for various computer vision tasks.

Multi-sensor Adaptability

#

Multi-sensor adaptability in depth completion focuses on developing methods that generalize well across diverse sensor modalities. This is crucial because real-world deployments often involve various sensors with differing characteristics (e.g., LiDAR, RGB-D cameras), each producing depth data with unique properties such as resolution, density, and noise levels. A truly adaptable system should handle these differences without requiring extensive retraining for each sensor type. This necessitates techniques that disentangle sensor-specific information from the underlying scene structure. Approaches might involve using a foundation model pre-trained on a large and diverse dataset to establish a general understanding of 3D scenes and then using sensor-specific modules for fine-tuning or adaptation. Another key element is the development of sensor-agnostic representations, capable of encoding depth information from any sensor type in a consistent manner. Finally, success hinges on rigorous evaluation across a variety of datasets and sensors to demonstrate genuine generalization capabilities. Few-shot learning techniques could be particularly effective here, allowing adaptation to new sensors with minimal labeled data.

Future Work: Radar

#

Extending depth completion methods to radar data presents a unique set of challenges and opportunities. Radar’s inherent sparsity and noisiness, unlike LiDAR or cameras, require novel approaches to data preprocessing and feature extraction. Direct application of existing techniques may prove ineffective due to the different physical principles involved. Developing robust methods for handling missing data and uncertainty in radar measurements is crucial. A promising avenue is to explore the fusion of radar data with other sensor modalities (e.g., cameras or LiDAR) to leverage complementary information for improved accuracy and density. This multimodal approach requires careful consideration of sensor registration and data fusion strategies, such as employing deep learning architectures specifically designed for sensor fusion. Furthermore, investigating the unique characteristics of radar signals (e.g., different frequencies, polarizations) can unlock specific advantages for depth estimation. Finally, evaluating and comparing these methods on diverse real-world datasets will be essential for proving the reliability and robustness of radar-based depth completion.

More visual insights

#

More on tables

This table presents the ablation study results comparing the performance of the proposed method using Euclidean and hyperbolic geometries. It shows the RMSE and MAE values for zero-shot (no training) and few-shot (1-shot, 10-shot, 100-shot) learning scenarios on NYU and KITTI datasets. This comparison highlights the impact of hyperbolic embedding on the model’s generalization and performance in low-data settings.

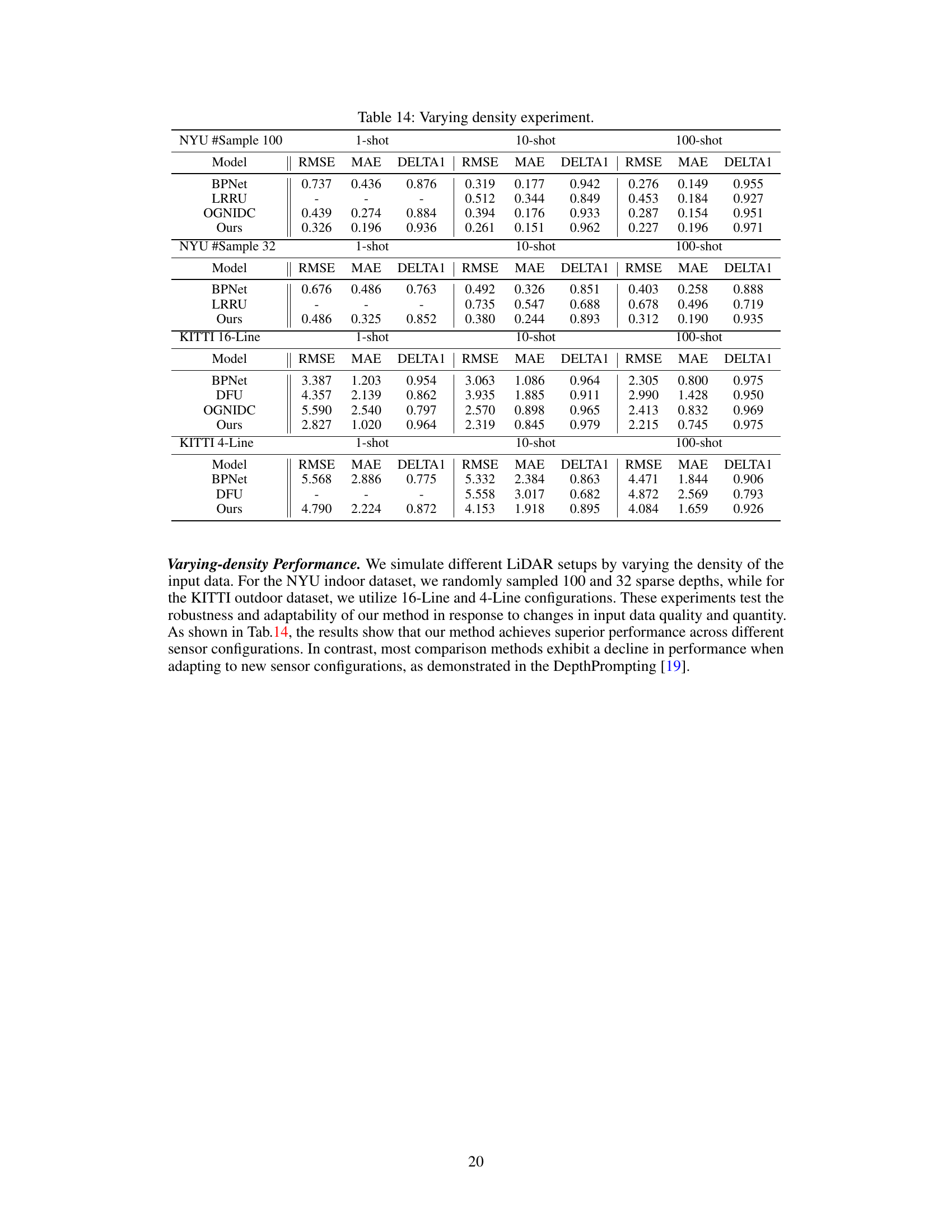
This table presents the results of few-shot learning experiments conducted without the use of dense ground truth (GT) depth data. The experiment aims to evaluate the model’s performance in a more realistic scenario where obtaining high-quality dense depth data is challenging, particularly for outdoor datasets. The results are shown for different sensor configurations (8-Line and 32-Line LiDAR), and different numbers of training shots (1-shot, 10-shot, and 100-shot). RMSE and MAE values are reported, demonstrating the model’s ability to adapt and generalize to new environments and sensor types, even with limited training data.

This table presents the average curvature values computed for multi-size affinity maps using the curvature generation blocks (Ck) in the proposed model. The curvatures are calculated for different kernel sizes (k = {3, 5, 7}) and for two datasets: NYU and KITTI. The values suggest that information from more distant regions tends to prefer lower curvature. This is because regions closer to the target require a more distinct hyperbolic space to prevent bleeding errors during depth propagation.

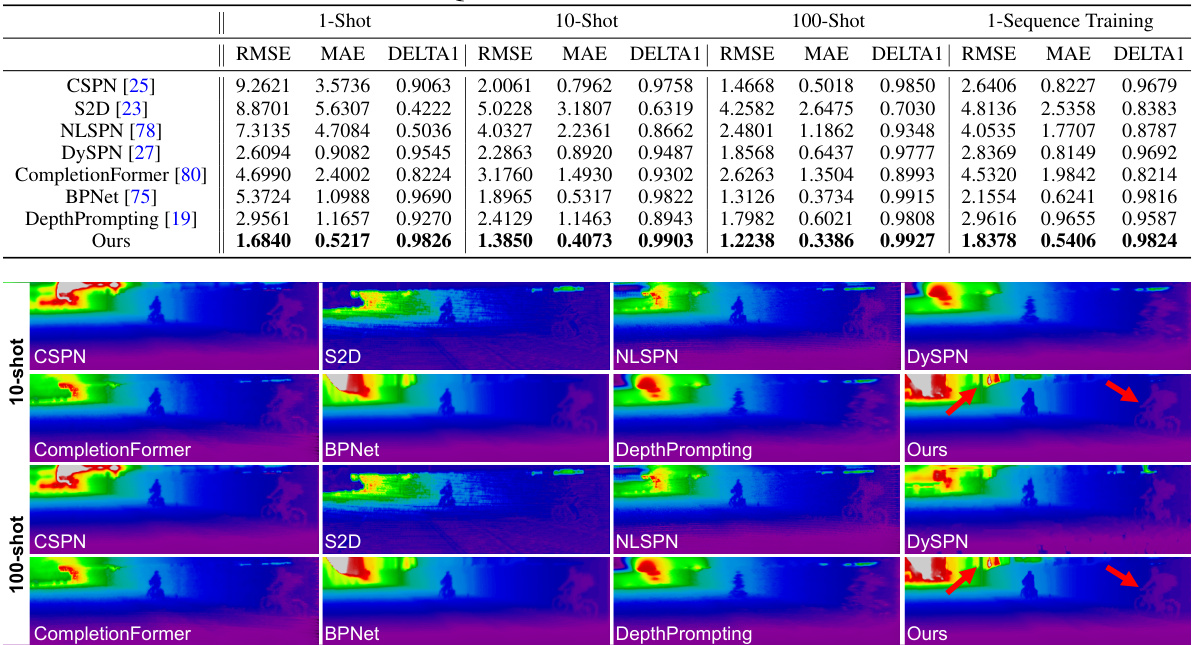
This table presents a quantitative comparison of different depth completion methods on the NYUv2 dataset. It shows the RMSE, MAE, and DELTA1 (inlier ratio) metrics for each method under various training scenarios: 1-shot, 10-shot, 100-shot, and 1-sequence training. The results demonstrate the performance of each method in terms of accuracy and robustness when trained with limited data.

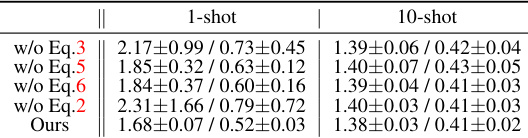
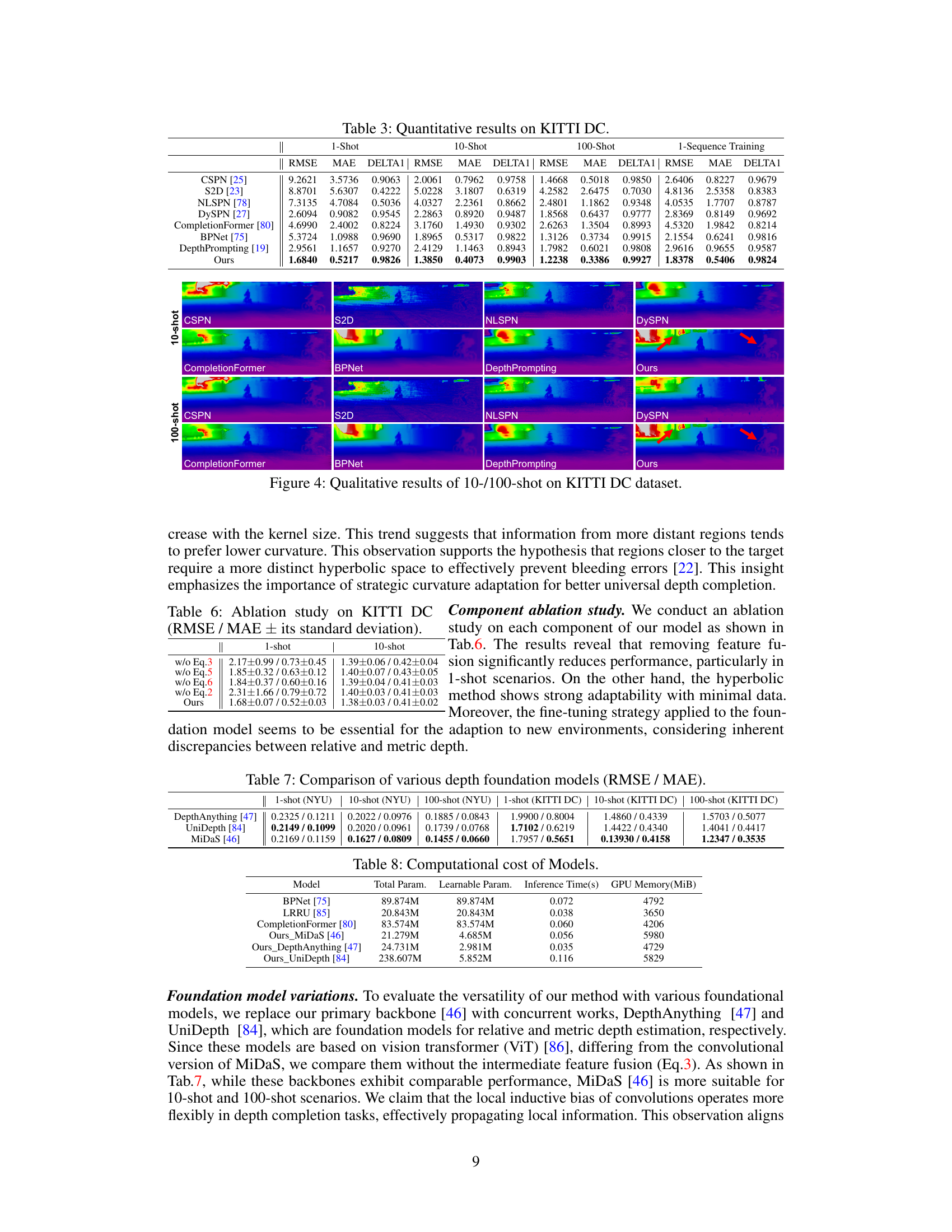
This ablation study analyzes the impact of each component (Eq.3, Eq.5, Eq.6, and Eq.2) on the overall performance of the proposed method. It evaluates the model’s performance with different components removed, showing the contribution of each part to the final result, particularly in 1-shot and 10-shot scenarios on the KITTI dataset.

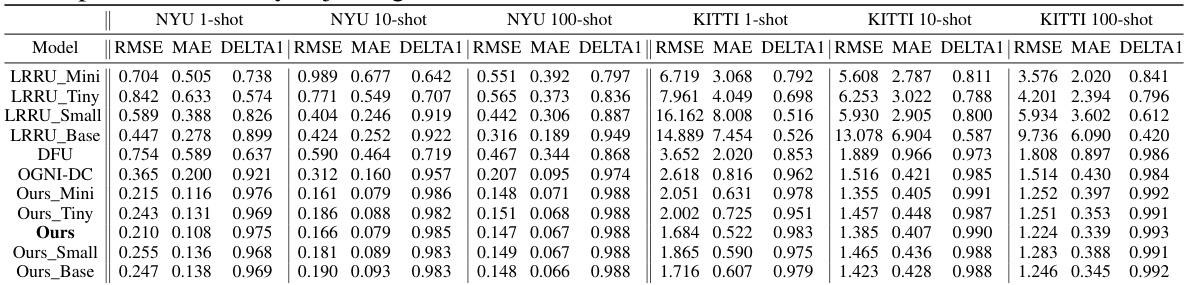
This table compares the performance of different depth foundation models (DepthAnything, UniDepth, and MiDaS) on the NYU and KITTI datasets using 1-shot, 10-shot, and 100-shot learning scenarios. The results show the RMSE and MAE values, indicating the accuracy of depth estimation for each model and training scenario. It highlights the varying performance across different models and dataset.

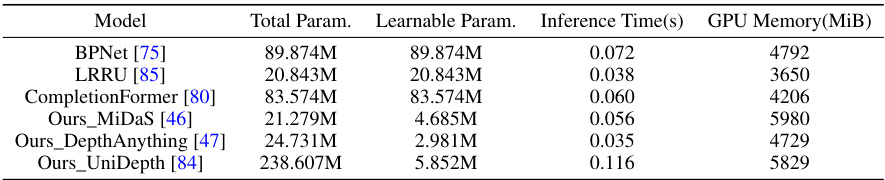
This table presents a comparison of the computational costs among different depth completion models. It shows the total number of parameters, the number of learnable parameters, the inference time (in seconds), and the GPU memory consumption (in MB) for each model. The models compared include BPNet, LRRU, CompletionFormer, and three variants of the proposed model (Ours) using different foundation models (MiDaS, DepthAnything, UniDepth). This allows for a quantitative assessment of the efficiency and resource requirements of each approach.

This table presents a quantitative comparison of different depth completion methods on the NYUv2 dataset. The comparison is performed under various training scenarios (1-shot, 10-shot, 100-shot, and 1-sequence training), demonstrating the performance of each method in low data regimes. Metrics used include RMSE, MAE, and DELTA1 (inlier ratio). The results highlight the performance of the proposed method, ‘Ours’, in comparison to state-of-the-art (SoTA) approaches.

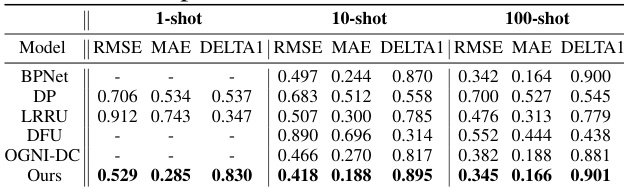
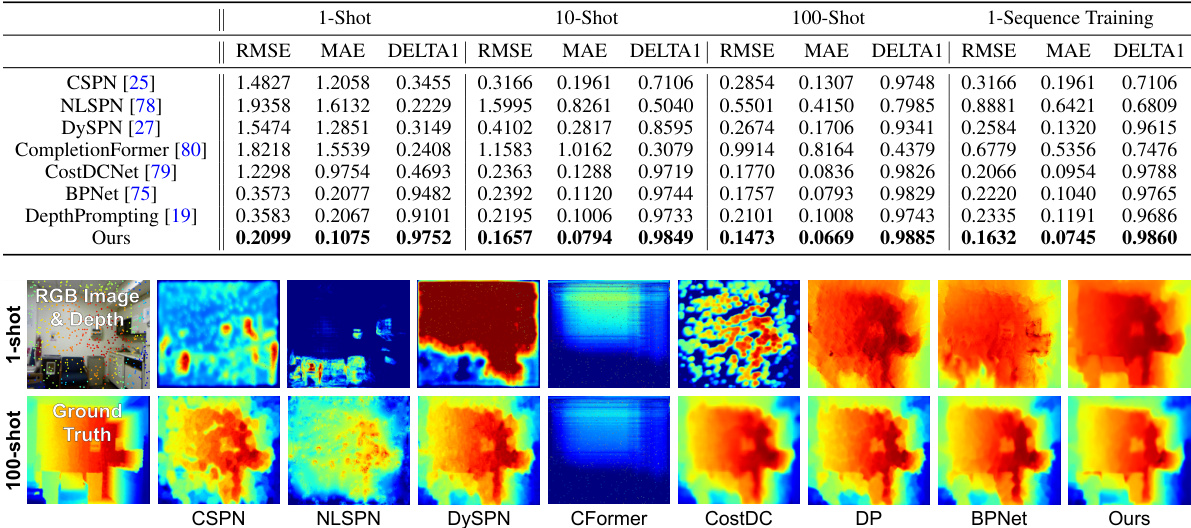
This table presents the results of the proposed UniDC model on the SUN RGB-D dataset. It shows a comparison of the model’s performance (RMSE, MAE, DELTA1) against other state-of-the-art methods (DP, LRRU, DFU, OGNIDC) under various few-shot learning settings (1-shot, 10-shot, 100-shot). The SUN RGB-D dataset is known for its diversity in terms of sensor types, environments, and data density, making it a good benchmark for evaluating the generalizability of depth completion methods.

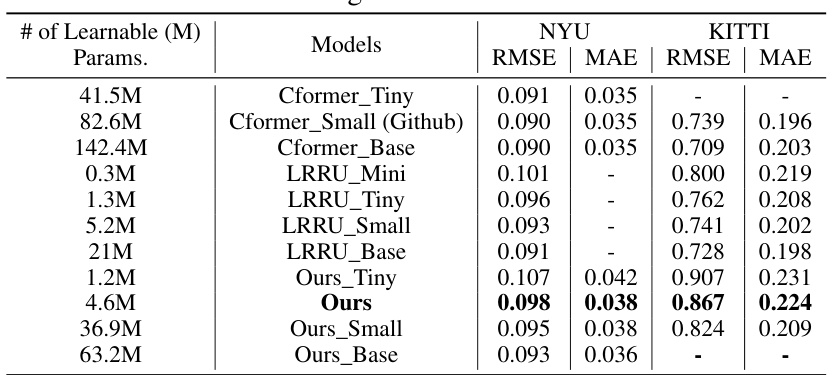
This table presents the performance comparison of different models (Cformer_Tiny, Cformer_Small, Cformer_Base, LRRU_Mini, LRRU_Tiny, LRRU_Small, LRRU_Base, Ours_Tiny, Ours, Ours_Small, Ours_Base) on NYU and KITTI datasets using full dataset training. The results are evaluated using RMSE and MAE metrics to assess the model’s accuracy in depth estimation. The number of learnable parameters for each model is also listed.

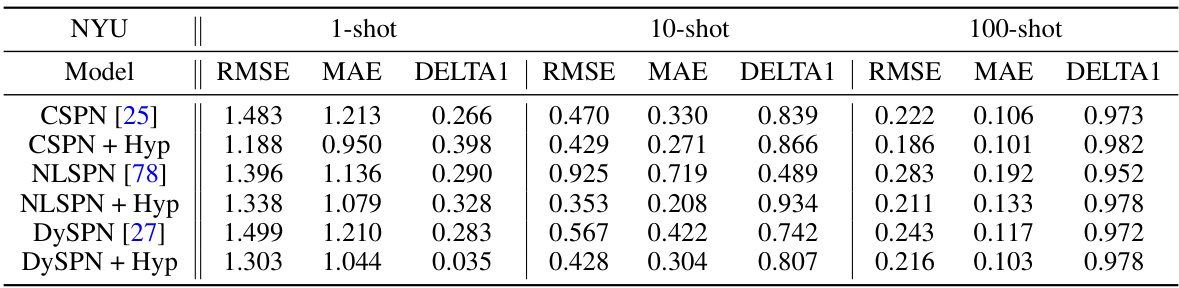
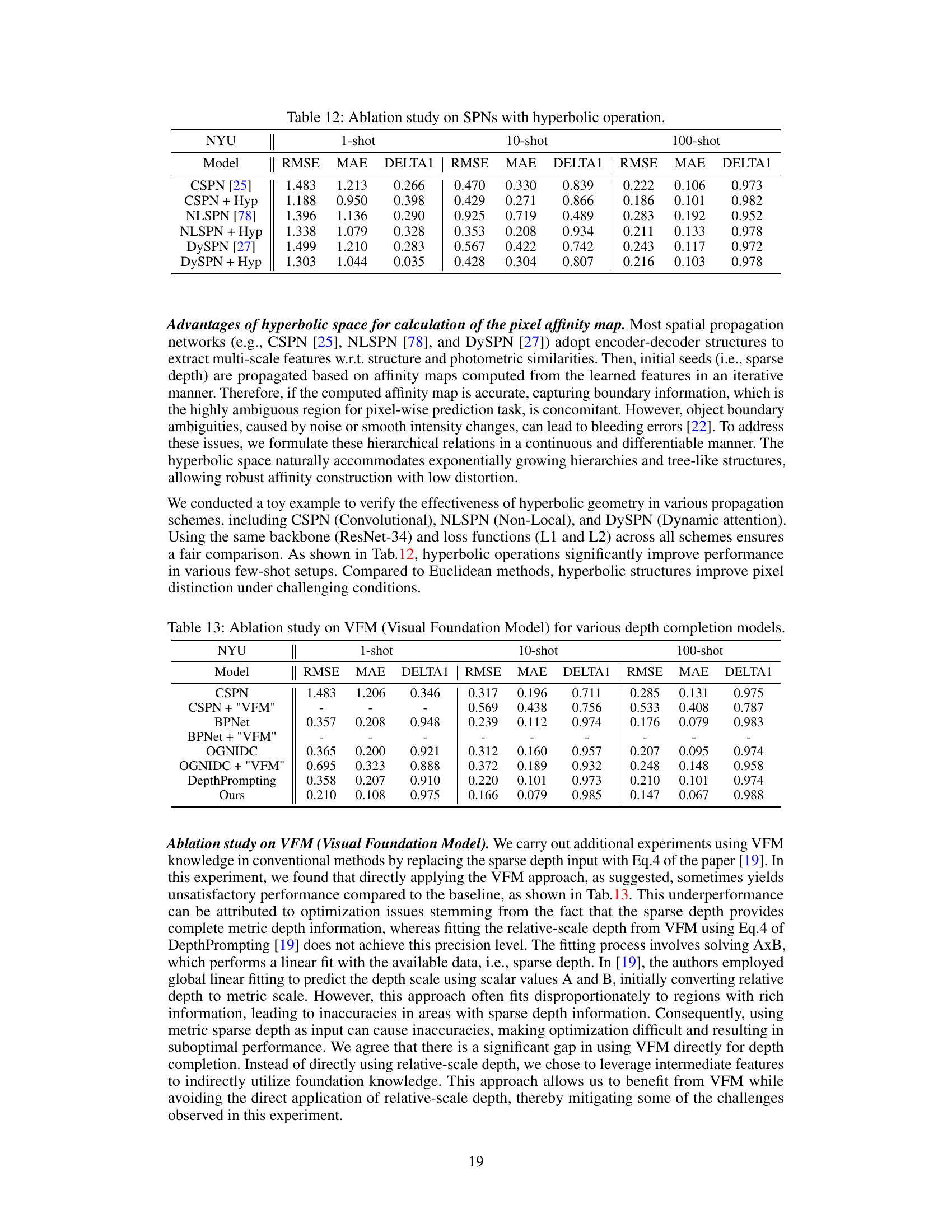
This table presents the ablation study results on different spatial propagation networks (SPNs) with and without hyperbolic operations. It compares the performance of CSPN, NLSPN, and DySPN, both with and without the addition of hyperbolic geometry, across 1-shot, 10-shot, and 100-shot learning scenarios. The metrics used for comparison include RMSE, MAE, and DELTA1, which represent the root mean squared error, mean absolute error, and inlier ratio, respectively. The results demonstrate the effectiveness of hyperbolic operations in improving the accuracy and robustness of depth completion, particularly in low-data regimes.

This ablation study compares the performance of different spatial propagation networks (SPNs), namely CSPN, NLSPN, and DySPN, both with and without the integration of hyperbolic operations. The results demonstrate the effectiveness of hyperbolic geometry in enhancing the accuracy of depth map prediction, especially in low-data scenarios.

This table presents a quantitative comparison of different depth completion methods on the NYUv2 dataset. The comparison considers various training scenarios, including 1-shot, 10-shot, 100-shot, and 1-sequence training. The evaluation metrics used are RMSE, MAE, and DELTA1, representing the root mean squared error, mean absolute error, and inlier ratio, respectively. The table showcases the performance of the proposed method (Ours) against several state-of-the-art (SOTA) methods across different training regimes, highlighting the method’s adaptability to few-shot learning scenarios.

Full paper

#