Fast Rates in Stochastic Online Convex Optimization by Exploiting the Curvature of Feasible Sets

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in online convex optimization because it bridges the gap between existing logarithmic and square-root regret bounds. By leveraging the curvature of feasible sets, it offers a new avenue for achieving faster convergence rates. This opens up exciting possibilities for improving existing algorithms and developing more efficient solutions for various applications.

Visual Insights

#

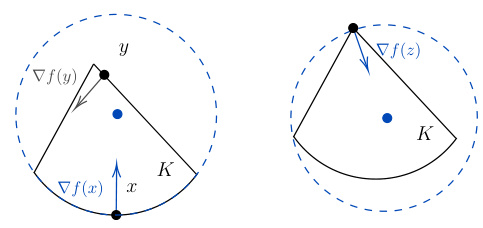
The left figure shows that K is sphere-enclosed facing x*, but K is not sphere-enclosed facing y. The right figure shows that K is sphere-enclosed facing z. Note that the notion of sphere-enclosedness is a local property defined for each point of the boundary of convex bodies, in contrast to the definition of strong convexity.

This table compares the regret upper bounds derived in this paper’s work to those found in existing literature. It shows the regret bound achieved under different conditions (stochastic, adversarial, corrupted stochastic environments), feasible set types (ellipsoid, strongly convex, sphere-enclosed, uniformly convex), and loss function characteristics. The table highlights the improvements achieved by the new approach proposed in the paper.

In-depth insights

#

Curvature Exploitation

#

The concept of ‘Curvature Exploitation’ in online convex optimization is a powerful technique for improving the convergence rate of algorithms. By leveraging the curvature of either the loss function or the feasible set, or ideally both simultaneously, algorithms can achieve logarithmic regret instead of the typical square root of T regret. This is particularly valuable when dealing with problems having strongly convex loss functions or feasible sets with well-defined boundary curvature. The research explores conditions under which curvature can be effectively exploited, proposing innovative analyses and demonstrating the significant performance gains achievable. A key aspect is the adaptive nature of algorithms that leverage curvature; they dynamically adjust to the underlying structure rather than relying on pre-defined parameters. This adaptive quality is crucial for practical applications where the precise level of curvature is often unknown or varies throughout the optimization process. The theoretical bounds derived offer a quantitative measure of how much performance improvement can be expected under certain curvature conditions. The study’s findings highlight the importance of considering geometric properties when developing efficient online convex optimization algorithms, opening avenues for designing and analyzing new, faster-converging methods.

Adaptive Algorithms

#

Adaptive algorithms, in the context of online convex optimization, represent a significant advancement in handling scenarios with unknown or varying curvature. They dynamically adjust their parameters based on the observed data, unlike traditional methods that rely on pre-defined settings. This adaptability is crucial for achieving optimal performance across diverse problem landscapes where the curvature of loss functions or feasible sets might change over time. The strength of adaptive algorithms lies in their ability to leverage problem-specific characteristics, leading to faster convergence rates and improved regret bounds compared to non-adaptive counterparts. This is particularly beneficial in situations where assumptions on strong convexity or other regularity conditions might not hold perfectly, or where the curvature is uncertain. The design and analysis of these algorithms often involve sophisticated techniques, combining elements of online learning, optimization theory, and sometimes even tools from information theory, to characterize the trade-offs between adaptation speed and performance guarantees. A key challenge in developing effective adaptive algorithms is balancing the exploration-exploitation dilemma – the need to learn about the problem structure while simultaneously minimizing the cumulative loss. Ultimately, the success of adaptive algorithms hinges on their ability to effectively capture relevant problem dynamics and translate them into efficient parameter adjustments, resulting in solutions that are both robust and efficient.

Regret Bounds

#

The core of the research paper revolves around regret bounds, a crucial concept in online convex optimization. The authors meticulously analyze and derive novel regret bounds for various scenarios, demonstrating significantly improved performance compared to existing methods. Their analysis leverages the curvature of feasible sets, a unique approach that distinguishes this work. The derived bounds showcase a fascinating transition: from logarithmic rates in stochastic settings with specific conditions on the curvature of the feasible set, to √T rates in adversarial environments, bridging the gap between strongly convex and non-convex scenarios. The bounds elegantly incorporate factors such as corruption levels and the uniform convexity of the feasible set, providing a comprehensive and nuanced understanding of the problem. This detailed analysis underscores the significant contribution in advancing the theoretical understanding and practical applications of online convex optimization.

OCO Advancements

#

OCO (Online Convex Optimization) advancements are significantly shaped by the interplay between algorithm design and the properties of the optimization landscape. Exploiting curvature in either loss functions or feasible sets is a major theme, leading to improved regret bounds beyond the standard O(√T). This is particularly evident in the development of algorithms adaptive to curvature, achieving logarithmic regret under specific conditions. However, these improvements often hinge on assumptions about the data generation process (e.g., stochastic vs. adversarial) or the structure of the feasible set (e.g., strong or uniform convexity). A key challenge remains to develop robust algorithms that deliver fast rates without relying on strong, often unrealistic, assumptions. Future research should focus on bridging this gap, potentially through more sophisticated adaptive techniques or the integration of curvature information from both the loss functions and the feasible set simultaneously. Understanding the relationship between curvature and regret is central to pushing the boundaries of OCO.

Future Research

#

Future research directions stemming from this work could explore relaxing the sphere-enclosed condition, perhaps by considering more general curvature notions or exploring alternative sufficient conditions. Investigating the tightness of regret bounds further, particularly for non-stochastic settings and uniformly convex sets, would also be valuable. Extending the analysis to encompass non-convex loss functions or handle more complex constraints would significantly broaden the applicability of these results. Finally, a key direction would be developing efficient algorithms that directly leverage the curvature of both the feasible sets and loss functions, moving beyond the currently-used universal online learning techniques. This could potentially lead to faster convergence rates and enhanced practical performance.

More visual insights

#

More on figures

This figure shows a convex body K (feasible set) and its minimum enclosing sphere BK (facing the optimal decision x*). The sphere’s center is at x* + (1/(2γ*))∇f°(x*), and its radius is ||∇f°(x*)||/(2γ*). The gradient of the expected loss function at x*, ∇f°(x*), points from x* towards the center of BK, illustrating the sphere-enclosed condition. This condition is key to achieving logarithmic regret bounds in the paper.

This figure illustrates a scenario where the optimal decision x* lies on the boundary of the feasible set K, and the gradient of the expected loss function, ∇f°(x*), points towards the exterior of the negative normal cone -NK(x*). This situation represents a case where the sphere-enclosed condition, crucial for achieving logarithmic regret bounds, is not satisfied because the gradient vector does not point toward the interior of the feasible set K around x*. The condition ∇f°(x*) ∈ int(-NK(x*)) (gradient inside the negative normal cone) is generally sufficient to satisfy the sphere-enclosed condition, thus guaranteeing fast convergence rate.

Full paper

#