↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Standard graph neural networks (GNNs) struggle with the challenge of extending shift equivariance from images to graphs due to the lack of a natural notion of translation. Existing spectral GNNs, while using linear filters that commute with graph functional shifts, lose this property due to non-linear activation functions. This limitation affects the model’s ability to learn effectively from graph data with symmetries.
This research introduces nonlinear spectral filters (NLSFs) designed to address this limitation. NLSFs are built using novel analysis and synthesis techniques that fully respect graph functional shifts. This design achieves full equivariance, leading to improved model performance. The method introduces a new transferable spectral domain, which significantly enhances generalizability and performance across various benchmark tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in graph machine learning and geometric deep learning. It introduces a novel approach to designing GNNs that are fully equivariant to graph functional shifts, offering improved generalization and reduced complexity. The proposed methods have demonstrated superior performance over existing GNNs, paving the way for advancements in various applications.
Visual Insights#
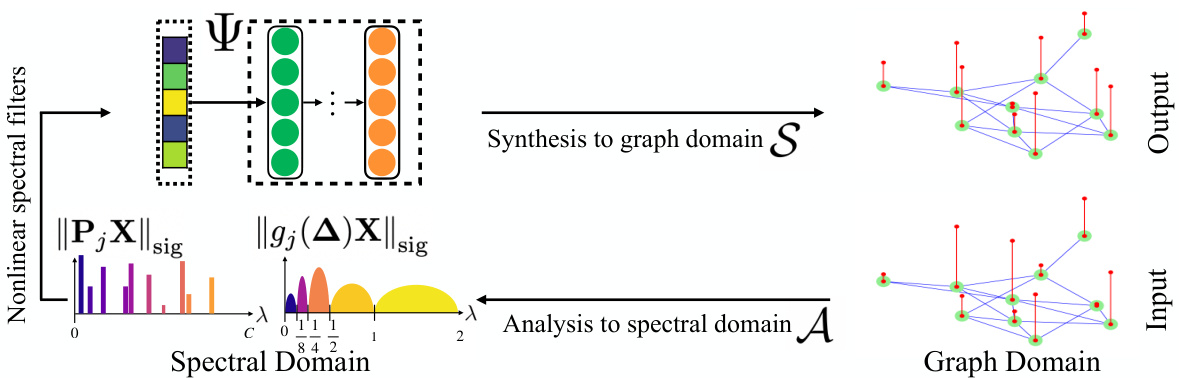
The figure illustrates the process of nonlinear spectral filtering for graph equivariant machine learning. It starts with node features X in the graph domain. These features are then analyzed (A) by projecting them onto eigenspaces, resulting in a spectral representation. A nonlinear function, Ψ, transforms this spectral representation. Finally, a synthesis operation (S) reconstructs the processed graph-level signal from the transformed spectral representation.
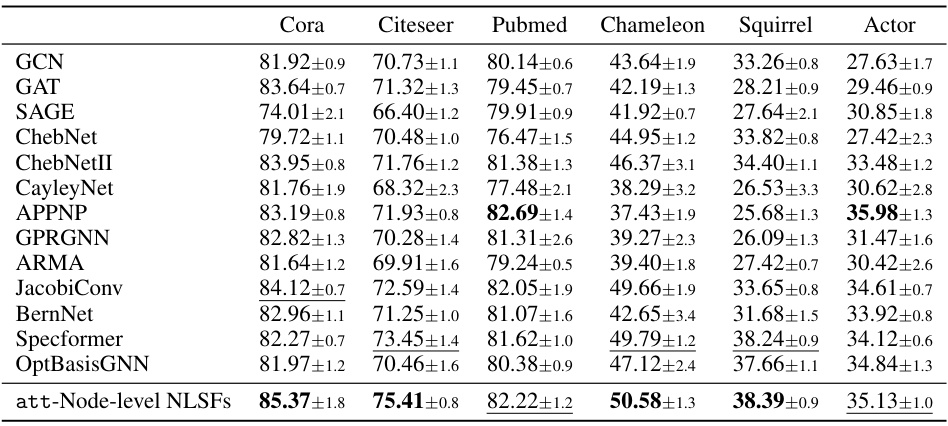
This table presents the results of semi-supervised node classification experiments on six datasets (Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor). It compares the performance of the proposed att-Node-level NLSFs against several state-of-the-art spectral graph neural networks (GNNs) such as GCN, GAT, SAGE, ChebNet, and others. The table shows the classification accuracy (with standard deviations) achieved by each method on each dataset. The results demonstrate that the att-Node-level NLSFs generally outperform or achieve comparable performance to existing GNNs across various datasets, showcasing their effectiveness in node-level classification tasks.
In-depth insights#
Graph Shift Equiv#
The concept of “Graph Shift Equivariance” explores the symmetries inherent in graph-structured data and how these symmetries can be leveraged in machine learning models. Unlike images with their inherent translational symmetry, graphs lack a clear spatial domain. Therefore, the focus shifts to functional shifts, which are unitary operators that commute with a chosen graph shift operator. Equivariant models respecting these functional shifts would be robust to different node orderings, a significant advantage in graph analysis where node ordering is arbitrary. This framework provides a formal way to extend the notion of shift equivariance from convolutional neural networks (CNNs) to graphs, offering the potential for more efficient and generalizable models that naturally capture the underlying symmetries of graph data. The key challenge is constructing nonlinear operations that preserve this functional equivariance, as standard activation functions break this symmetry. The paper addresses this by introducing nonlinear spectral filters (NLSFs) with the goal of creating fully equivariant and universally approximating graph neural networks.
Nonlinear Spectral#
The concept of “Nonlinear Spectral” processing within the context of graph neural networks (GNNs) represents a significant departure from traditional linear spectral methods. Linear spectral GNNs leverage the graph’s spectral decomposition—its eigenvalues and eigenvectors—to define filters that operate in the frequency domain, offering efficiency and mathematical elegance. However, the inherent linearity limits their ability to capture complex, nonlinear relationships within graph data. Nonlinear Spectral techniques address this limitation by incorporating nonlinear activation functions or transformations into the spectral filtering process. This introduction of nonlinearity allows the model to learn more intricate patterns and potentially improve representational power and generalization, which is critical for complex graph-structured data. A key challenge is ensuring that these nonlinear operations maintain the equivariance properties that make spectral methods attractive. Ideally, the model should remain invariant to the specific ordering of nodes in the graph while preserving the underlying structure and relationships. This balance between expressive power and maintaining essential graph-theoretic properties is the core focus of research in this area. The introduction of transferability between different graphs is another significant advance, as nonlinear spectral methods often struggle with the inherent non-uniformity of graphs. Transferable methods offer enhanced flexibility and allow for more effective learning across a wider range of graph datasets.
Transferability#
The concept of ’transferability’ in the context of graph neural networks (GNNs) centers on the ability of a model trained on one graph to generalize effectively to other, unseen graphs. Existing spectral GNNs struggle with transferability because their spectral representations are tied to specific graph structures, hindering their ability to adapt to new graphs with different node counts or connectivity patterns. This paper introduces non-linear spectral filters (NLSFs) that address this limitation. Unlike linear filters, NLSFs employ a novel form of spectral representation that is independent of specific graph Laplacians, enabling transferability between graphs with distinct structures. This is achieved through analysis and synthesis transforms that map signals between node and spectral domains in a way that’s independent of specific eigenbases. The proposed NLSFs offer a substantial improvement in performance on node and graph classification benchmarks, demonstrating the practical value of their approach to improve transferability in GNNs.
Laplacian Attention#
The concept of ‘Laplacian Attention’ in graph neural networks is intriguing. It suggests a mechanism to adaptively weigh different Laplacian matrix parameterizations within a model. The choice between standard and normalized Laplacian matrices is critical, as their spectral properties differ significantly. This approach likely addresses the transferability challenge of spectral GNNs, as different graph structures might benefit from different Laplacian choices. Performance improvements are expected in heterogeneous graph scenarios where node degree distribution varies significantly, because the attention mechanism would automatically select the most suitable Laplacian for each particular graph. The effectiveness of ‘Laplacian Attention’ would likely hinge on the design of the attention mechanism, its ability to learn the optimal weighting based on graph characteristics, and the model’s overall architecture. Universal Approximation Theorems likely play a part in explaining this model’s capacity to learn complex graph structures through weighted combinations of simpler filters based on different Laplacian formulations.
Future Extensions#
Future research directions stemming from this work could explore several promising avenues. Extending the NLSF framework to handle different types of graph signals beyond node features is crucial, potentially incorporating edge features, higher-order structures, or even temporal dynamics. Investigating alternative spectral representations and their associated symmetries would enrich the framework, enabling more flexible modeling of complex graph structures and improving generalizability. The current approach relies heavily on eigenvalue decomposition; thus, exploring more efficient techniques to manage this computational cost is critical for scaling up to truly massive graphs. Finally, a deeper theoretical understanding of the relationship between graph symmetries, activation functions, and expressivity is needed, particularly concerning the universal approximation properties of NLSFs. This could lead to innovative filter designs that surpass current performance benchmarks and further enhance the expressive power of graph neural networks.
More visual insights#
More on figures
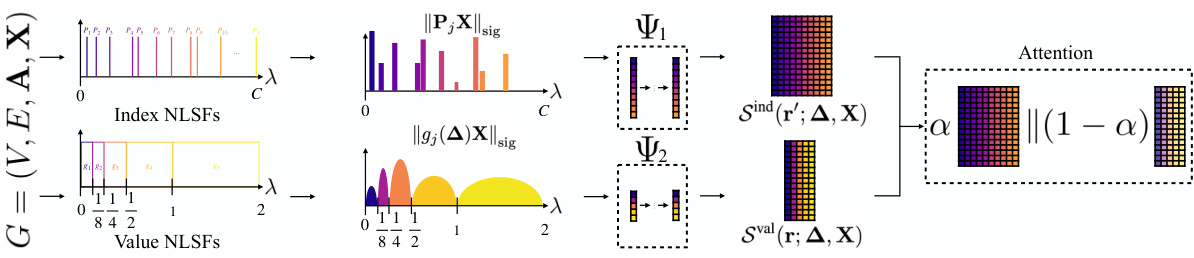
This figure illustrates the process of nonlinear spectral filters (NLSFs) used for equivariant machine learning on graphs. It starts with a graph G and its node features X. The analysis step (A) projects these features onto eigenspaces. Then a nonlinear function Ψ transforms these spectral coefficients. Finally, a synthesis step (S) reconstructs a graph-domain representation from the modified spectral coefficients, resulting in a new output. This process leverages the eigenspaces and a filter bank for analysis and synthesis, leading to a method for processing signals equivariantly.
This figure illustrates the process of nonlinear spectral filtering for graph machine learning. It shows how node features (X) are first analyzed (A) by projecting them onto eigenspaces. The resulting spectral representation then undergoes a nonlinear transformation (Ψ), which maps a sequence of frequency coefficients to another sequence of frequency coefficients. Finally, these transformed coefficients are synthesized (S) back into the graph domain to produce the output. This process ensures equivariance to graph functional shifts.

This figure illustrates the process of nonlinear spectral filters (NLSFs) for equivariant machine learning on graphs. The input is a graph G with node features X. The analysis step (A) projects the node features onto eigenspaces. Then, a function Ψ maps a sequence of frequency coefficients to another sequence of coefficients. Finally, the synthesis step (S) synthesizes these coefficients to obtain the output in the graph domain.
This figure illustrates the process of nonlinear spectral filtering for graph machine learning. It starts with node features X, which are first analyzed (A) by projecting them onto the eigenspaces of the graph’s shift operator. Then, a nonlinear function (Ψ) transforms the resulting spectral coefficients, before they are synthesized (S) back into the graph domain, producing the output.
More on tables
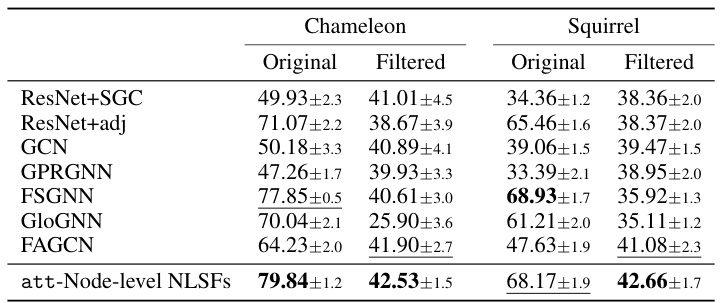
This table presents a comparison of node classification performance on the original and filtered versions of the Chameleon and Squirrel datasets. The filtering process removes duplicate nodes identified in the original datasets. The table shows the classification accuracy (with 95% confidence intervals) of several GNN methods (ResNet+SGC, ResNet+adj, GCN, GPRGNN, FSGNN, GloGNN, FAGCN, and att-Node-level NLSFs) on both the original and filtered datasets. The results highlight the impact of data leakage due to duplicate nodes in the original datasets and demonstrate the robustness of the proposed att-Node-level NLSFs to this issue.
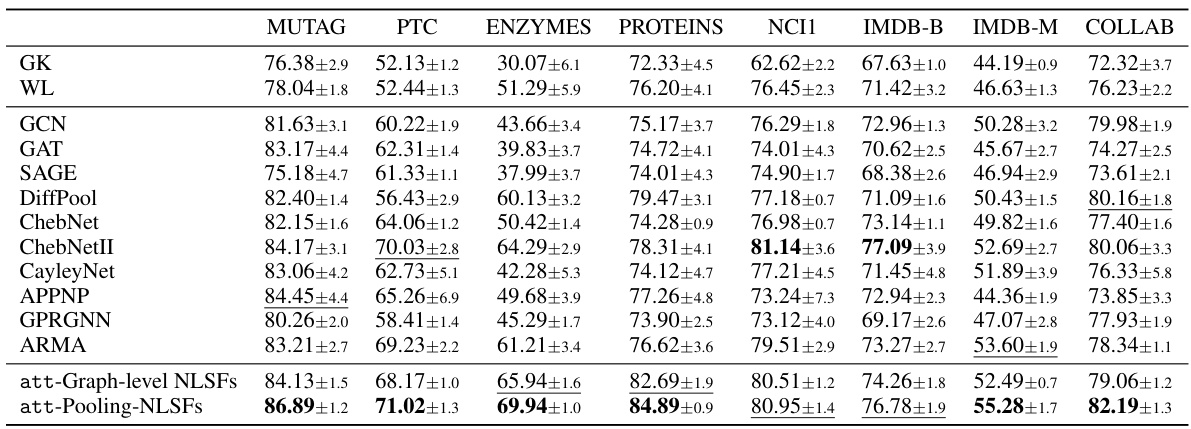
This table presents the results of graph classification experiments using various methods, including geometric graph convolutional networks (GCNs) and the proposed nonlinear spectral filters (NLSFs). The accuracy is reported for eight different benchmark datasets, showing the performance of different methods in classifying graph structures. The table allows for a comparison of the proposed method (att-Pooling-NLSFs) to several state-of-the-art baseline algorithms, including WL, GK, GCN, GAT, SAGE, DiffPool, ChebNet, ChebNetII, CayleyNet, APPNP, GPRGNN, and ARMA.
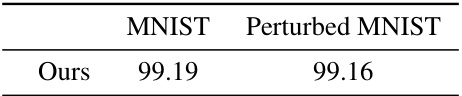
This table presents the MNIST classification accuracy achieved using NLSFs on both clean and perturbed MNIST datasets. The ‘Ours’ row indicates the accuracy obtained by the proposed method, showing high accuracy on both datasets, highlighting the robustness of NLSFs to perturbations.
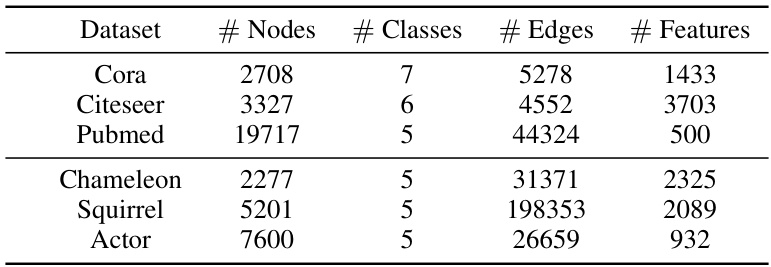
This table presents the results of semi-supervised node classification experiments conducted on six different datasets (Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor). The accuracy of the proposed att-Node-level NLSFs is compared against several other state-of-the-art graph neural networks (GNNs), including GCN, GAT, SAGE, ChebNet, ChebNetII, CayleyNet, APPNP, GPRGNN, ARMA, JacobiConv, BernNet, Specformer, and OptBasisGNN. The table shows the mean accuracy and standard deviation across multiple trials for each model and dataset, providing a comprehensive comparison of performance.
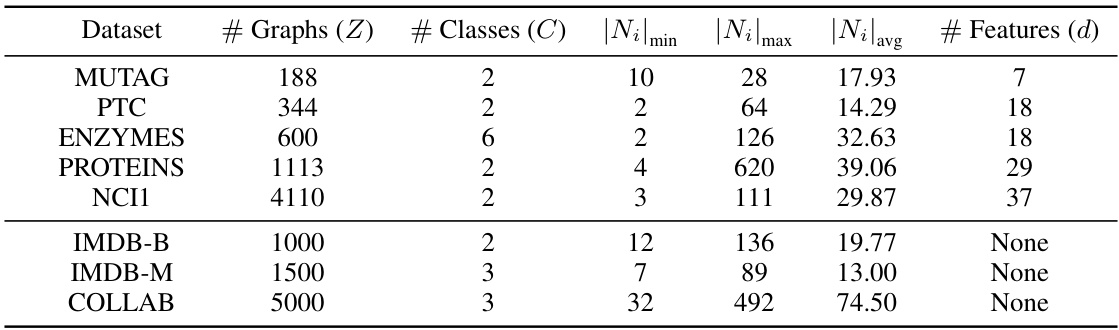
This table presents the statistics of eight graph classification datasets used in the paper’s experiments. For each dataset, it lists the number of graphs, the number of classes, the minimum and maximum number of nodes per graph, the average number of nodes per graph, and the number of features per node. The datasets cover various domains, including bioinformatics (MUTAG, PTC, ENZYMES, PROTEINS, NCI1) and social networks (IMDB-B, IMDB-M, COLLAB).
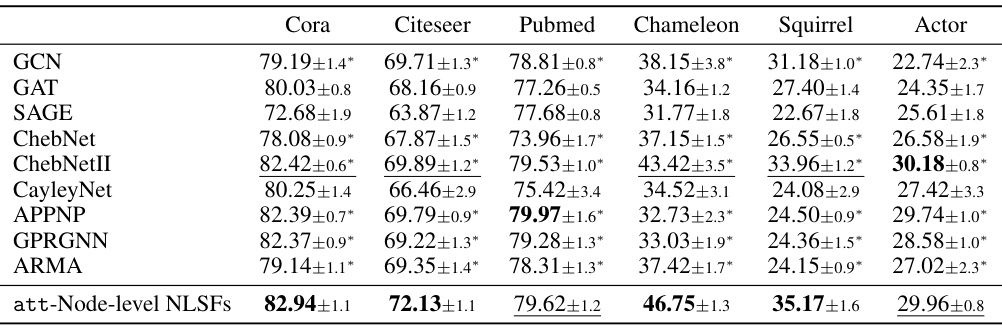
This table presents the results of semi-supervised node classification experiments on six datasets (Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor). The table compares the performance of the proposed att-Node-level NLSFs against several state-of-the-art GNN methods, showing classification accuracy with 95% confidence intervals across 10 random dataset splits. The results illustrate the superior performance of att-Node-level NLSFs on various datasets.
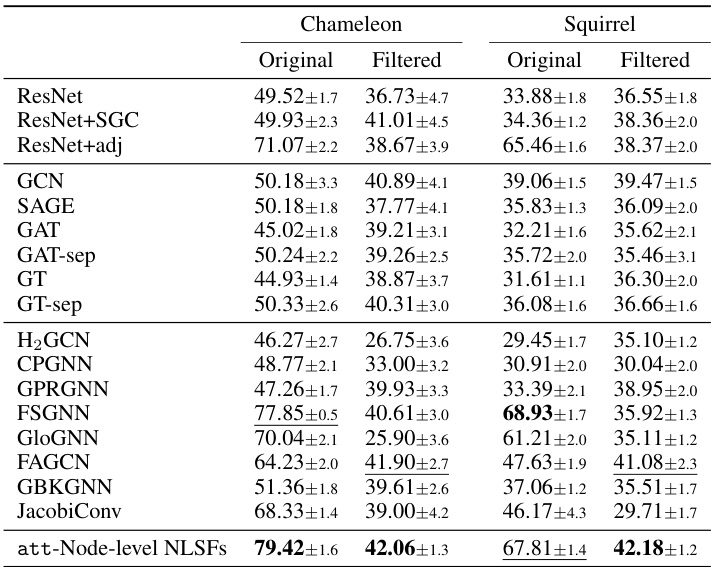
This table compares the performance of different graph neural network models on node classification tasks using the Chameleon and Squirrel datasets. It’s notable that these datasets were re-evaluated in a later study [77] to address issues related to data leakage in the original dense split setting. This table thus presents classification results on both the original and the filtered versions of the datasets, allowing for a more reliable comparison. The models compared include various GNN architectures, and the results are presented as average accuracy with standard deviation.
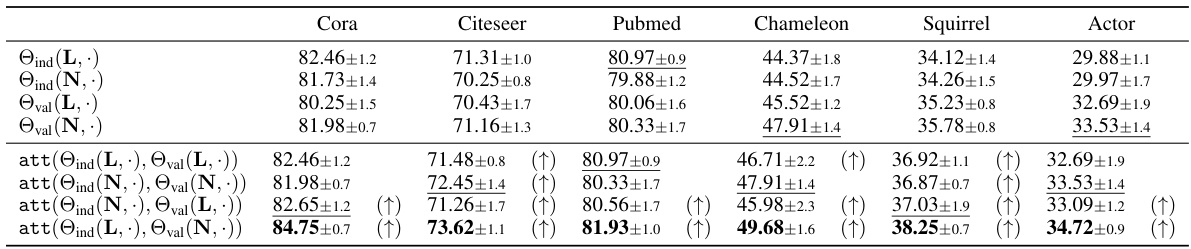
This ablation study compares the performance of Node-level NLSFs using different Laplacians (combinatorial Laplacian L and normalized Laplacian N) and parameterizations (Index and Value). It shows the impact of Laplacian attention on improving classification accuracy. The results are presented for six different datasets: Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor. The (↑) symbol indicates that Laplacian attention improved the result.

This table presents the results of an ablation study on graph classification using Graph-level NLSFs. It compares the performance of Index NLSFs and Value NLSFs, both with and without Laplacian attention, across eight benchmark datasets. The goal is to analyze the impact of different parameterizations and the Laplacian attention mechanism on graph classification accuracy. The results show that Laplacian attention generally improves performance.

This table presents the results of semi-supervised node classification experiments on six datasets: Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor. The table compares the performance of the proposed att-Node-level NLSFs against several other state-of-the-art Graph Neural Networks (GNNs) including GCN, GAT, SAGE, ChebNet, ChebNetII, CayleyNet, APPNP, GPRGNN, ARMA, JacobiConv, BernNet, Specformer, and OptBasisGNN. The accuracy for each method is presented as an average across 10 random splits, accompanied by a 95% confidence interval. The results showcase the superior performance of att-Node-level NLSFs compared to the baseline GNN models on several of the datasets.
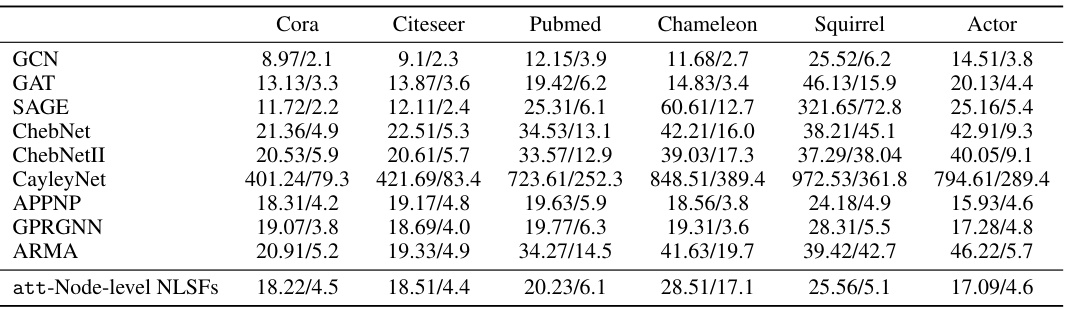
This table presents the results of semi-supervised node classification experiments using various Graph Neural Networks (GNNs) on six benchmark datasets: Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor. The table shows the average classification accuracy (with standard deviation) achieved by each GNN on each dataset. The datasets represent different types of graphs and levels of difficulty, allowing for a comprehensive comparison of GNN performance.
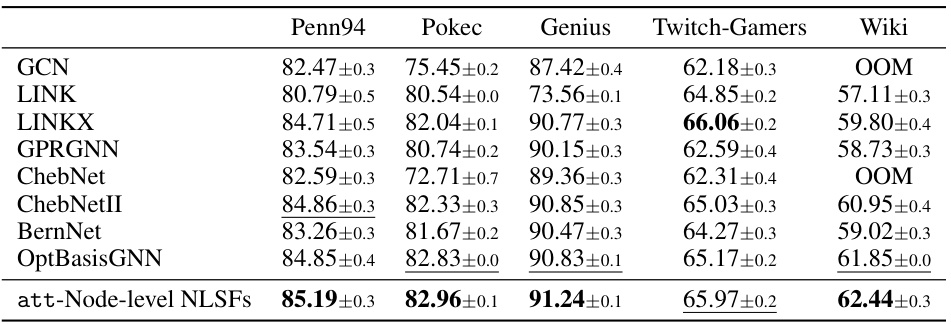
This table presents the results of semi-supervised node classification experiments on six different datasets (Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor). The accuracy of several graph neural network (GNN) models is compared, including GCN, GAT, SAGE, ChebNet, ChebNetII, CayleyNet, APPNP, GPRGNN, ARMA, JacobiConv, BernNet, Specformer, OptBasisGNN, and the proposed att-Node-level NLSFs. The table shows the mean accuracy and standard deviation for each method on each dataset, providing a quantitative comparison of the performance of different GNN architectures for node classification.

This table presents the results of graph classification experiments using diagonal NLSFs, specifically focusing on index-by-index Index-NLSFs and band-by-band Value-NLSFs. It compares the performance of these methods with and without Laplacian attention. The results are presented for several benchmark datasets, illustrating the impact of the different approaches on classification accuracy. The use of the Laplacian attention mechanism is highlighted by the (↑) symbol to indicate an improvement in performance compared to methods without this attention.

This table presents the results of semi-supervised node classification on six datasets (Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor). It compares the accuracy of the proposed att-Node-level NLSFs against several other state-of-the-art graph neural network models (GCN, GAT, SAGE, ChebNet, ChebNetII, CayleyNet, APPNP, GPRGNN, ARMA, JacobiConv, BernNet, Specformer, OptBasisGNN). The results show the average accuracy and standard deviation over ten random splits, demonstrating the superior performance of att-Node-level NLSFs on several of the datasets, especially the more challenging heterophilic datasets (Chameleon, Squirrel, Actor).

This table presents the results of semi-supervised node classification experiments on six datasets: Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor. The table compares the accuracy of the proposed Node-level NLSFs (with Laplacian attention) against several existing state-of-the-art spectral graph neural networks (GNNs). Each dataset’s results are presented with average accuracy and a 95% confidence interval over ten random splits. The performance of the NLSFs is highlighted and contrasted with the results of GCN, GAT, SAGE, ChebNet, and other GNNs.

This table presents the results of semi-supervised node classification experiments on six datasets: Cora, Citeseer, Pubmed, Chameleon, Squirrel, and Actor. The table compares the performance of the proposed att-Node-level NLSFs against several other state-of-the-art Graph Neural Networks (GNNs), including GCN, GAT, SAGE, ChebNet, ChebNetII, CayleyNet, APPNP, GPRGNN, ARMA, JacobiConv, BernNet, Specformer, and OptBasisGNN. The accuracy is presented as the average classification accuracy ± standard deviation over 10 random dataset splits, showcasing the superior performance of the att-Node-level NLSFs, especially on the heterophilic datasets (Chameleon, Squirrel, Actor).
Full paper#



















