↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current automated theorem proving methods often rely on short-sighted heuristics, leading to suboptimal or distracting subgoals and hindering the discovery of longer proofs. This limits their ability to solve complex mathematical problems effectively. The search-based approaches often get stuck in exploring a detailed proof of meaningless intermediate conjecture and wastes time.
To overcome these challenges, this paper introduces POETRY (PrOvE Theorems RecursivelY), a novel recursive approach. POETRY tackles theorems level-by-level, initially searching for a verifiable proof sketch at each level, replacing detailed proofs of intermediate conjectures with placeholders. This incremental approach allows for efficient exploration of the proof space and significant performance gains are observed. The experiments demonstrate that POETRY achieves a 5.1% improvement in the average proving success rate and increases the maximum proof length substantially.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in automated theorem proving and neural theorem proving. It presents POETRY, a novel recursive approach that significantly improves the efficiency and success rate of automated theorem proving, especially for complex theorems. The method’s potential to solve longer proofs and its adaptability to various formal environments make it highly relevant to current trends in the field and pave the way for more efficient and robust automated reasoning systems.
Visual Insights#

This figure compares two different approaches for proving theorems: step-by-step and recursive. The step-by-step method (a) treats the proof as a linear sequence of steps, only verifiable upon completion. The recursive method (b), in contrast, breaks down the proof into smaller, independently verifiable ‘proof sketches’. Each sketch proves a sub-goal, temporarily replacing the detailed proof of intermediate conjectures with placeholders (‘sorry’). This allows for incremental verification and potentially discovering longer proofs.

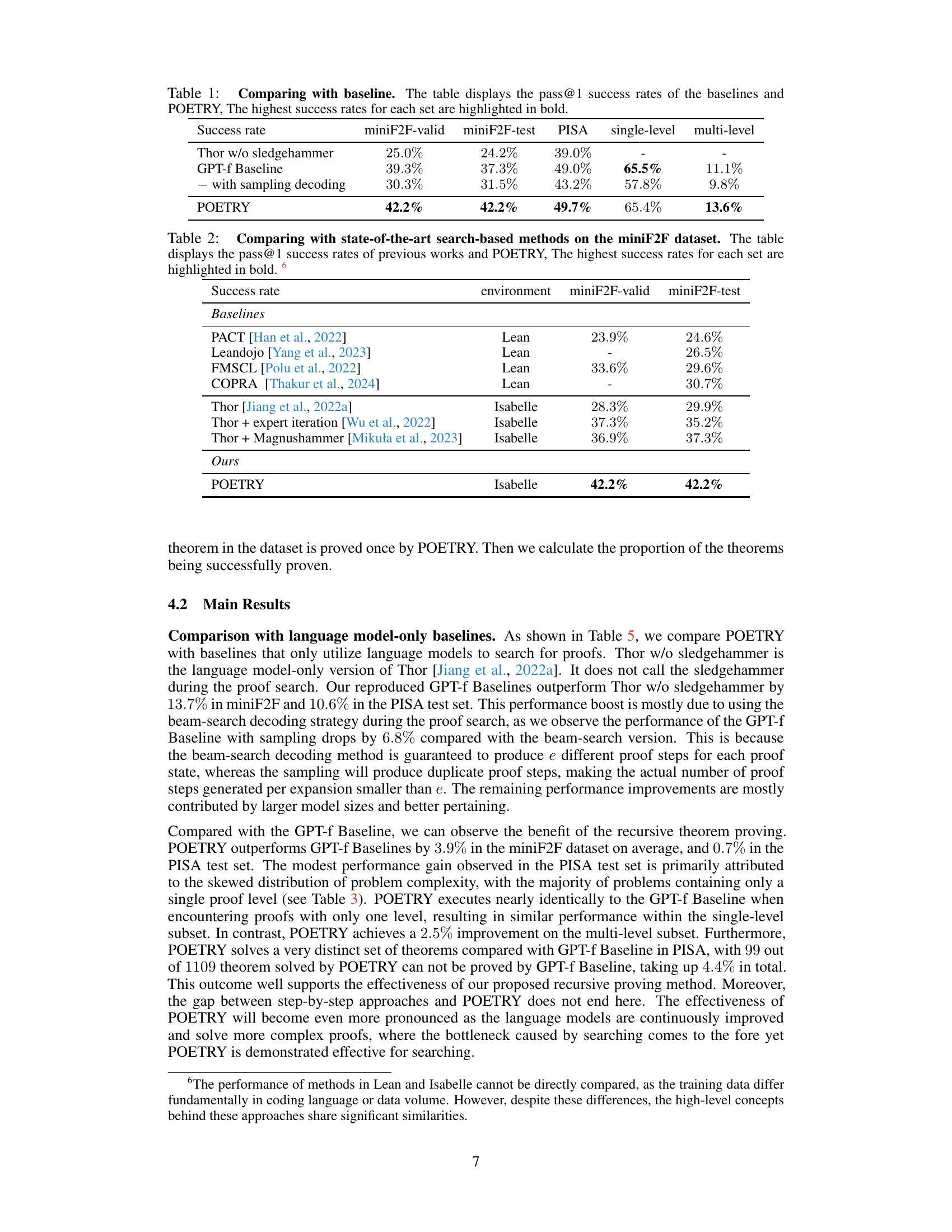
This table compares the performance of POETRY against several baseline methods (Thor w/o sledgehammer, GPT-f Baseline with sampling decoding, and GPT-f Baseline with beam search decoding) and shows the pass@1 success rate for each method on three different datasets: miniF2F-valid, miniF2F-test, and PISA (split into single-level and multi-level subsets). The highest success rate for each dataset is highlighted in bold, indicating POETRY’s superior performance.
In-depth insights#
Recursive Proof#
The concept of “Recursive Proof” in the context of automated theorem proving offers a novel approach to tackling complex mathematical problems. Instead of a linear, step-by-step approach, a recursive method breaks down the proof into a hierarchy of smaller, more manageable sub-proofs. Each sub-proof addresses a specific part of the overall theorem, with placeholders used for intermediate conjectures that are proven recursively at deeper levels. This incremental strategy contrasts with existing methods that often get trapped in local optima or distracted by seemingly promising but ultimately unhelpful subgoals. The recursive nature allows for a more holistic and structured exploration of the search space, potentially uncovering longer, more intricate proofs than previously possible. Verification is enhanced by checking the validity of each proof sketch at each level, before proceeding to subsequent levels. This contrasts with the step-by-step approach which only allows for verification once the whole proof is complete. This recursive approach is analogous to how humans often solve complex problems, decomposing them into simpler sub-problems and solving them individually before assembling the final solution.
Isabelle/POETRY#
Isabelle/POETRY represents a novel approach to automated theorem proving, integrating the Isabelle theorem prover with a recursive proof generation technique. Isabelle provides the formal mathematical environment, facilitating rigorous verification of proof steps. POETRY’s core innovation lies in its recursive, level-by-level approach, tackling complex theorems by first generating a verifiable proof sketch at each level, temporarily replacing detailed subproofs with placeholders. This incremental strategy avoids the pitfalls of short-sighted heuristics, which often lead to suboptimal or distracting subgoals in traditional step-by-step methods. By focusing on verifiable proof outlines, and then recursively proving the intermediate conjectures, POETRY efficiently manages the search space and increases the likelihood of finding longer, more complex proofs. The combination of Isabelle’s formal rigor and POETRY’s recursive strategy makes for a powerful and efficient system, showcasing promising advancements in automated theorem proving.
Recursive BFS#
The proposed recursive best-first search (BFS) algorithm represents a novel approach to neural theorem proving. Instead of a linear, step-by-step search, it iteratively explores proof sketches, focusing on the current level’s conjecture or subgoal. This incremental approach tackles the theorem hierarchically by deferring proofs of intermediate conjectures (using placeholders like ‘sorry’) to subsequent levels, enabling the algorithm to handle more complex proofs, resulting in longer maximum proof lengths. This recursive strategy contrasts with traditional step-by-step methods, which are prone to getting trapped in less relevant subproblems due to myopic heuristics. The ‘sorry’ tactic is crucial; it allows for verifiable proof outlines at each level. Importantly, the algorithm includes mechanisms for backtracking and status updates (OPEN, FAILED, HALF-PROVED, PROVED), reflecting the dynamic progress across various proof levels, demonstrating a robust and adaptable search strategy. The recursive BFS algorithm thus demonstrates a significant improvement in successfully finding longer proofs compared to traditional step-by-step approaches.
Experimental Setup#
A robust experimental setup is crucial for validating the claims of a research paper. In this context, a well-defined setup would begin by specifying the baselines used for comparison. Clearly identifying the baseline methods, such as previous state-of-the-art models or simpler approaches, allows for a fair evaluation of the proposed method’s performance. The choice of baseline methods should be justified, highlighting their relevance and ensuring they represent the current state-of-the-art. Details on data preprocessing, including any data cleaning, augmentation, or transformation techniques, should be meticulously documented. Hyperparameter settings should also be transparently reported, explaining the methods used to select them (e.g., grid search, random search, or Bayesian optimization). The evaluation metrics should be clearly defined and justified, ensuring their appropriateness for the specific research question. Finally, specifying the computational resources, including hardware and software configurations, ensures the reproducibility of the results by others.
Future Work#
Future research directions stemming from this paper could involve several key areas. Extending POETRY to other theorem provers like Lean or Coq would broaden its applicability and impact. This would require adapting the framework to handle the nuances of different proof languages and environments. A second crucial area is improving the recursive best-first search algorithm. While the current approach shows promise, enhancements focusing on more sophisticated heuristics, or incorporating advanced search techniques like Monte Carlo Tree Search (MCTS) could significantly improve efficiency and success rates. Addressing the issue of redundant proof steps generated by the greedy exploration strategy is another avenue of exploration; introducing a value function could prioritize more informative steps and prevent wasted computation. Finally, investigating the potential of combining POETRY with external solvers or knowledge bases could enhance its ability to tackle exceptionally complex theorems, unlocking the potential of this methodology to contribute to advanced mathematical problems in the future.
More visual insights#
More on figures
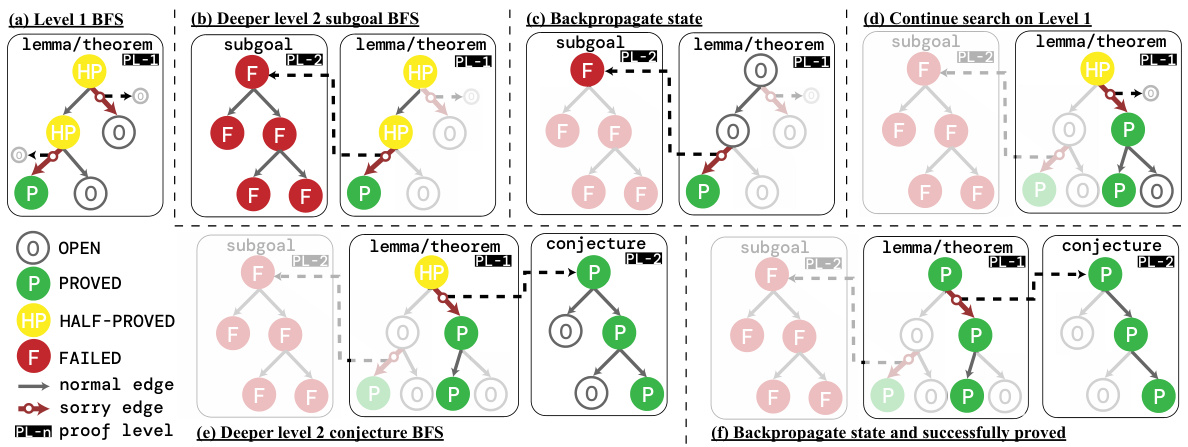
This figure illustrates the recursive best-first search (BFS) algorithm used in POETRY. It walks through a complete walkthrough example, showing how the algorithm searches for proof sketches at each level, handles failures, backpropagates information, and ultimately completes the proof by recursively solving intermediate conjectures.
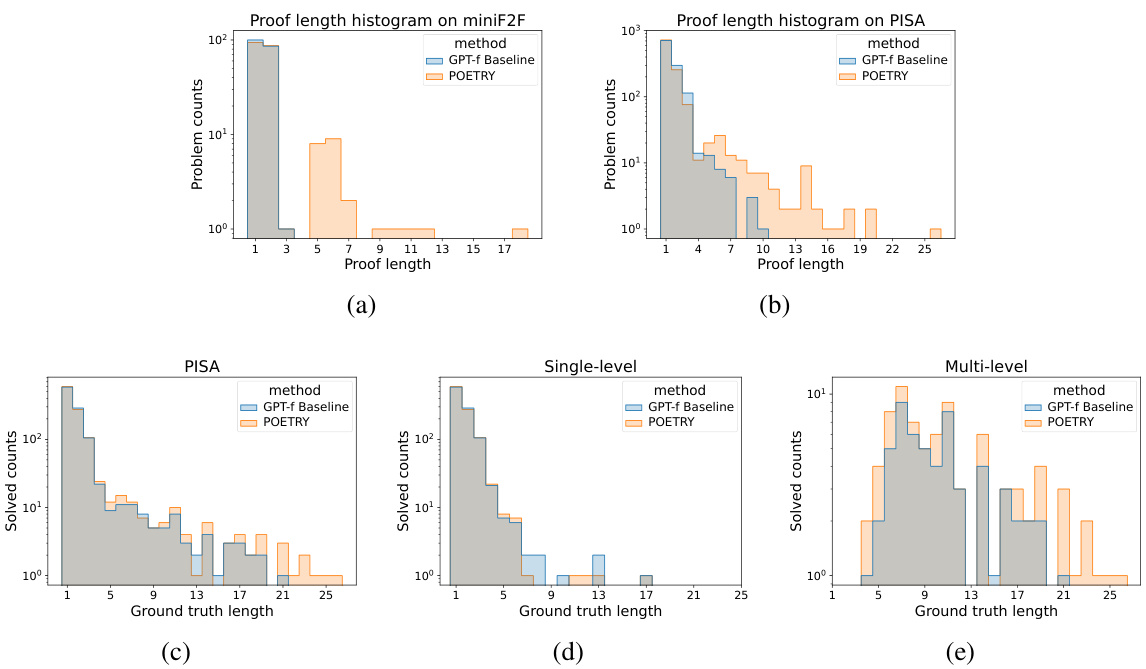
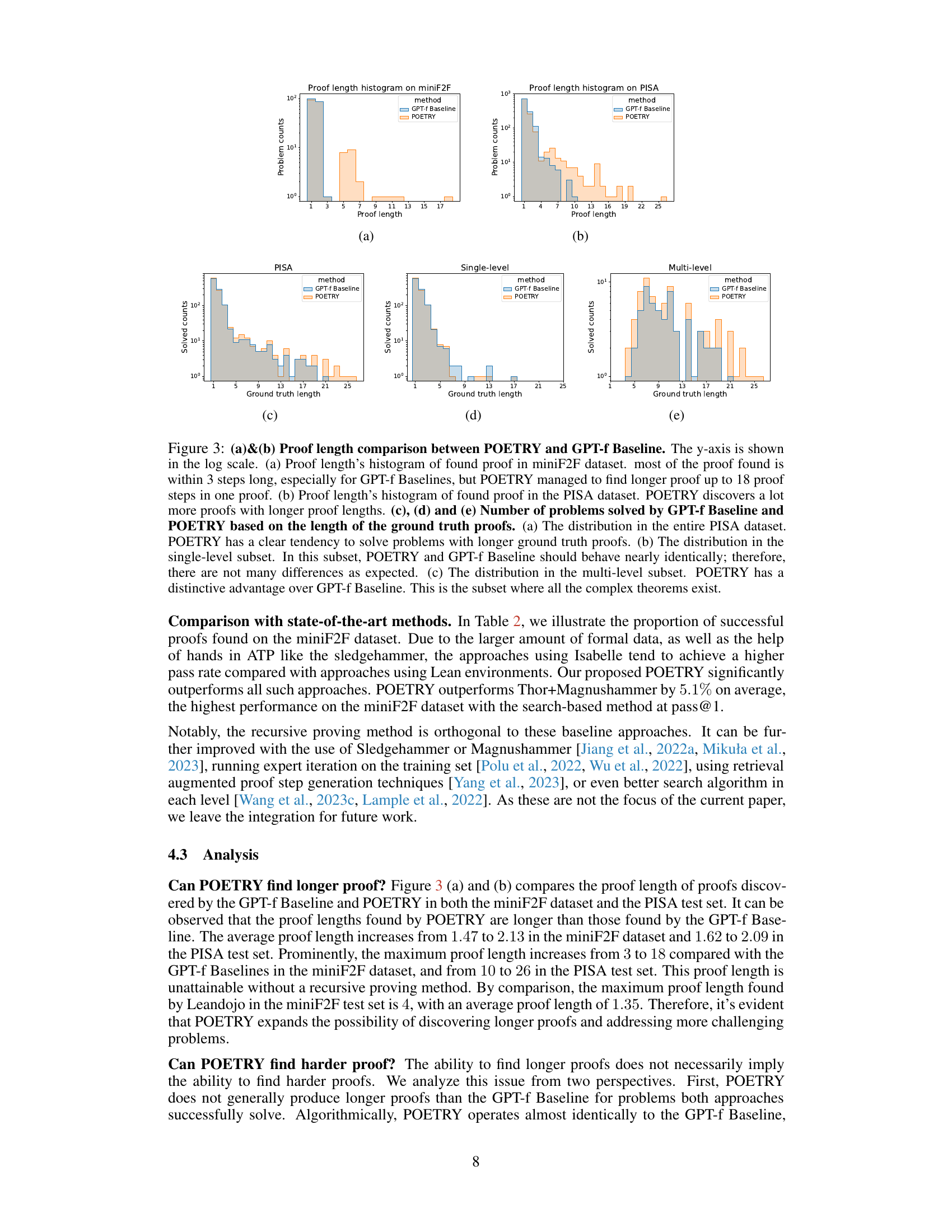
This figure compares the proof lengths found by POETRY and GPT-f Baseline on miniF2F and PISA datasets. It shows that POETRY finds significantly longer proofs than GPT-f Baseline, especially for more complex problems (multi-level subset of PISA). The y-axis uses a logarithmic scale to better visualize the distribution of proof lengths. Histograms illustrate the number of problems solved by each method for different ground truth proof lengths, highlighting POETRY’s superior performance on longer, more challenging proofs.
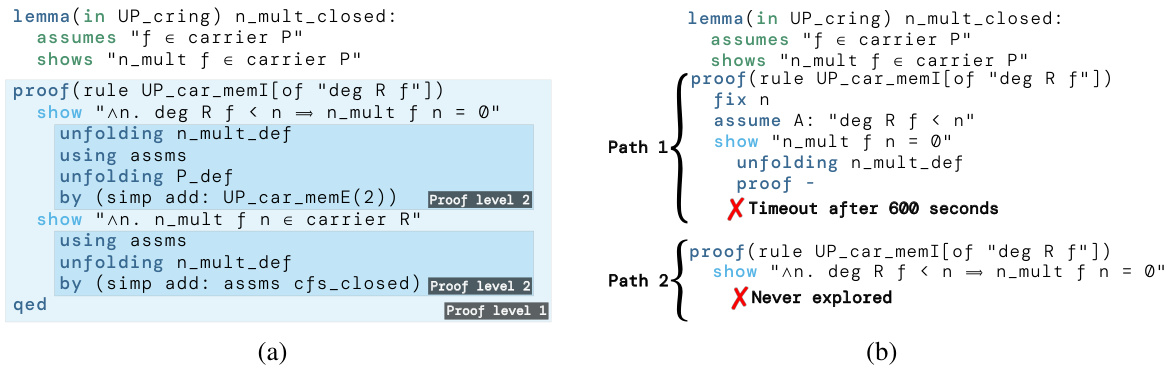
This figure compares the performance of POETRY and GPT-f Baseline on a specific theorem. POETRY successfully finds a recursive proof within 71.2 seconds, demonstrating its ability to decompose complex proofs into manageable subproblems. In contrast, GPT-f Baseline fails to find a proof within 600 seconds, highlighting the limitations of its step-by-step approach. The figure showcases two different failure paths taken by GPT-f Baseline, illustrating how it gets stuck exploring unproductive paths. This comparison emphasizes POETRY’s efficiency and capability to handle challenging theorems that are difficult for traditional methods.
This figure compares the proof lengths found by POETRY and GPT-f Baseline on miniF2F and PISA datasets. The histograms show that POETRY finds significantly more proofs with longer lengths, especially in the PISA dataset’s multi-level subset (more complex problems). The additional plots show the number of problems solved successfully, categorized by the ground truth proof lengths, highlighting POETRY’s ability to solve problems with longer ground truth proofs.

This figure illustrates the recursive best-first search (BFS) algorithm used in POETRY. It shows how the algorithm searches for proof sketches level by level, pausing when a sketch is found and recursively proving the skipped conjectures or subgoals at the next level. The figure uses different node states (OPEN, FAILED, PROVED, HALF-PROVED) and edge types (normal, sorry) to visually represent the search process and its progression.

This figure compares two approaches to theorem proving: step-by-step and recursive. The step-by-step approach (a) treats a proof as a linear sequence, only verifiable upon completion. The recursive approach (b) breaks the proof into verifiable sketches at each level, temporarily replacing sub-proofs with placeholders (‘sorry’) until later levels. This allows for incremental verification and potentially longer proofs.

This figure compares two approaches to proving theorems: step-by-step and recursive. The step-by-step method (a) linearly constructs a proof, only verifying its validity once complete. This can lead to exploring unproductive subgoals. The recursive method (b) incrementally builds a proof, creating verifiable ‘sketches’ at each level. Intermediate steps are temporarily marked as ‘solved’ (using a placeholder), deferring their proof to a later level. This allows for a more focused search at each level and can ultimately lead to longer, more complex proofs.

This figure compares step-by-step and recursive proof approaches. The step-by-step method (a) treats proof generation as a linear sequence of steps, only verifiable upon completion. The recursive method (b), in contrast, breaks the proof into verifiable sketches at different levels. Each level focuses on proving the current theorem or conjecture, temporarily deferring the proofs of intermediate steps (using placeholders like ‘sorry’) to subsequent levels. This incremental approach allows for more manageable proof construction and potential for finding longer, more complex proofs.

This figure compares step-by-step and recursive proof approaches. The step-by-step method treats a proof as a linear sequence of steps, only verifiable upon completion. In contrast, the recursive method breaks the proof into verifiable sketches at each level. Each level focuses on proving the current theorem or conjecture, temporarily replacing detailed proofs of intermediate conjectures with placeholders (‘sorry’). This incremental approach allows for tackling complex theorems by deferring sub-proofs to deeper levels, enhancing verifiability and potentially efficiency.

This figure compares two approaches for proving theorems: step-by-step and recursive. The step-by-step approach (a) treats the proof as a linear sequence, only verifiable at the end. The recursive approach (b) breaks the proof down into verifiable levels, with intermediate steps (‘sorry’ tactics) deferred to later levels. This incremental approach allows for tackling complex proofs more efficiently.

This figure compares two approaches to theorem proving: step-by-step and recursive. The step-by-step approach (a) treats the proof as a linear sequence of steps, delaying verification until completion. The recursive approach (b) breaks the proof down into verifiable sub-proofs (levels), each focusing on the current level’s theorem or conjecture, with more complex proofs deferred to subsequent levels, improving verifiability and potentially efficiency. This is done by using placeholder tactic ‘sorry’ for intermediate conjectures.

This figure compares step-by-step and recursive proof approaches for theorem proving. The step-by-step method treats the proof as a linear sequence, making verification impossible until completion. In contrast, the recursive method breaks the proof into verifiable sketches at each level, deferring subproofs to subsequent levels, thus enabling incremental progress and verification.

This figure illustrates the recursive best-first search algorithm used in POETRY. It shows how the algorithm searches for proof sketches level by level, pausing when a sketch is found and recursively searching for proofs of intermediate conjectures. The figure uses a tree structure to visualize the search process, with nodes representing proof states and edges representing proof steps. Different node colors represent the status of each node (OPEN, FAILED, PROVED, HALF-PROVED), and a ‘sorry’ edge indicates that a conjecture has been deferred to a lower level.
More on tables

This table compares the performance of POETRY against several baseline methods on three datasets: miniF2F-valid, miniF2F-test, and PISA. For the PISA dataset, results are further broken down into single-level and multi-level subsets based on proof complexity. The table shows the pass@1 success rate (percentage of problems solved in one attempt) for each method on each dataset/subset. The highest success rates for each dataset/subset are highlighted in bold. The baselines include Thor without sledgehammer and two versions of a GPT-f baseline (one with and one without sampling decoding).

This table compares the performance of POETRY against other state-of-the-art search-based neural theorem proving methods on the miniF2F dataset. It shows the pass@1 success rate (percentage of theorems correctly proven in a single attempt) for each method, broken down by the miniF2F-valid and miniF2F-test sets. The table highlights POETRY’s superior performance compared to existing methods across both datasets.
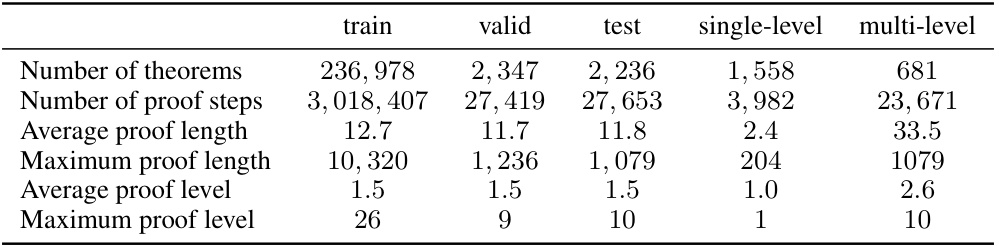
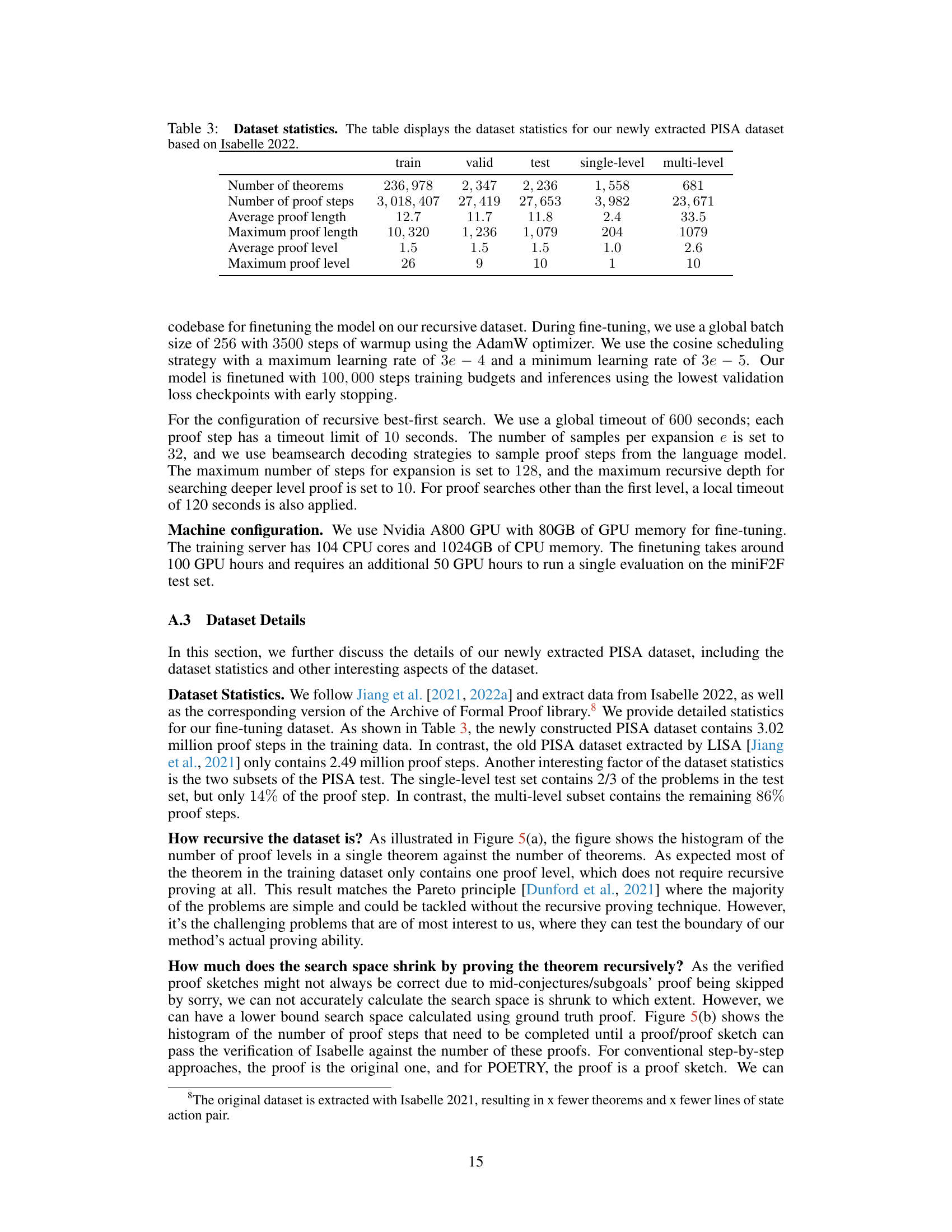
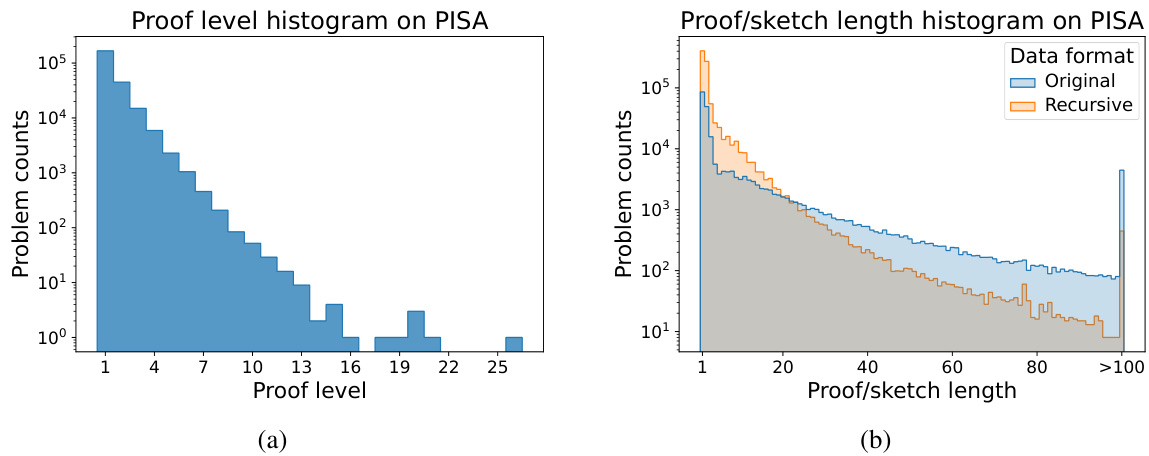
This table presents a statistical overview of the newly curated PISA dataset, which is based on Isabelle 2022. It provides the number of theorems, proof steps, average and maximum proof lengths, average and maximum proof levels for the training, validation, and test sets. Additionally, it breaks down these statistics for single-level and multi-level problems within the test set.

This table compares the performance of POETRY against other state-of-the-art search-based neural theorem provers on the miniF2F dataset. It shows the pass@1 success rate (the percentage of problems solved in a single attempt) for each method. The methods are categorized by the formal environment they use (Lean or Isabelle) and the results highlight POETRY’s superior performance.

This table compares the performance of POETRY against several baseline methods on three datasets: miniF2F (valid and test sets) and PISA (single-level and multi-level sets). The pass@1 metric represents the success rate of proving a theorem in a single attempt. The table highlights POETRY’s superior performance, particularly on the miniF2F datasets, showing a significant improvement over the baseline methods. The results also indicate that POETRY performs better with more complex, multi-level proofs within the PISA dataset.
Full paper#