↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep learning model training is computationally expensive and requires large datasets. Data selection aims to reduce these costs but traditional methods often compromise accuracy by neglecting the balance between bias and variance reduction, especially in high-dimensional finetuning. This paper focuses on data selection for the finetuning of pre-trained models, a context where less research has been done.
This paper introduces Sketchy Moment Matching (SkMM), a two-stage data selection method. First, gradient sketching identifies an informative low-dimensional subspace of the model’s parameter space. Then, moment matching selects samples that reduce variance within this subspace while maintaining low bias. Theoretically, they prove SkMM preserves fast-rate generalization. Empirically, experiments on synthetic and real vision tasks show SkMM outperforms existing data selection methods, demonstrating its effectiveness for reducing data volume and computational cost in deep learning finetuning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning and data selection. It offers a novel approach to efficiently select data for fine-tuning deep learning models, addressing the growing concerns of data volume and computational costs. The theoretical analysis and empirical results demonstrate a new variance-bias tradeoff perspective, opening avenues for future research in scalable and effective data selection strategies. The provably accurate method could significantly improve the efficiency of training and finetuning large models.
Visual Insights#
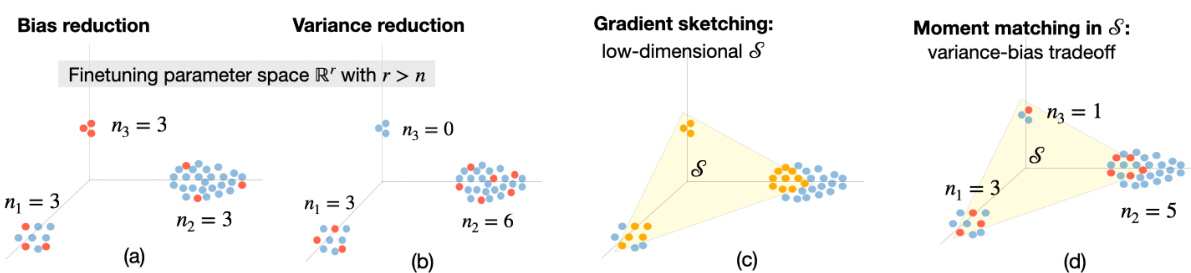
This figure illustrates the variance-bias tradeoff in high-dimensional finetuning data selection. It compares four scenarios: (a) bias reduction (uniform selection), (b) variance reduction (biased towards high-variance clusters), (c) gradient sketching (identifying a low-dimensional subspace with minimal bias), and (d) Sketchy Moment Matching (SkMM) which balances bias and variance within the subspace for optimal generalization.
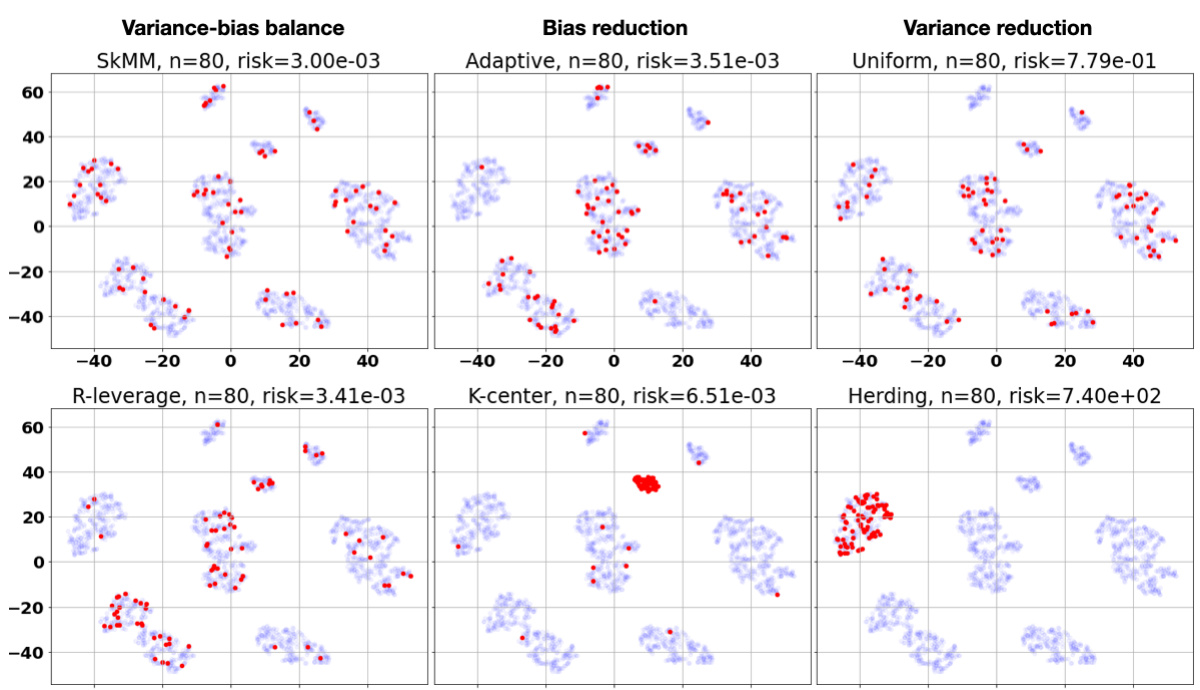
This table presents the empirical risk (LD(θs)) achieved by different data selection methods on a Gaussian Mixture Model (GMM) dataset for various sample sizes (n). It compares the performance of SkMM against baselines like uniform sampling, Herding, K-center, adaptive sampling, and leverage score sampling. The table highlights the impact of different data selection strategies on generalization performance, showing how SkMM balances the variance-bias tradeoff effectively.
In-depth insights#
Variance-Bias Tradeoff#
The concept of the variance-bias tradeoff is central to the paper’s exploration of data selection for finetuning. In high-dimensional settings, simply minimizing variance (as traditional methods do) is insufficient, leading to high bias due to the under-representation of the parameter space. The authors highlight that a balance is needed: reducing bias by exploring informative subspaces and then minimizing variance within those subspaces. This balance is achieved through their proposed SkMM (Sketchy Moment Matching) method. SkMM addresses this challenge in two stages: gradient sketching to identify informative low-dimensional subspaces and moment matching to ensure variance reduction within those subspaces. The theoretical analysis shows that this combined approach preserves fast-rate generalization, independent of the high-dimensional parameter space, making it efficient and effective. The variance-bias tradeoff thus becomes a crucial consideration, with the authors demonstrating the limitations of variance-focused approaches alone and highlighting SkMM’s ability to effectively navigate this tradeoff for optimal finetuning performance.
Gradient Sketching#
Gradient sketching, in the context of this research paper, is presented as a scalable and provably accurate method for dimensionality reduction within the high-dimensional parameter space of deep learning models. It leverages the concept of sketching to efficiently identify an informative low-dimensional subspace, thereby reducing computational costs associated with high-dimensional data analysis. The theoretical analysis demonstrates that gradient sketching, despite its simplicity, preserves the fast-rate generalization, achieving performance comparable to methods operating on the full high-dimensional space. This is a crucial step towards addressing the challenges of data selection for finetuning, where model parameters vastly outnumber available data points. The use of gradient sketching in the proposed data selection algorithm, SkMM, allows for fast exploration of the parameter space while mitigating the high computational cost associated with direct search in high dimensions. The method’s effectiveness is further substantiated by empirical results on both synthetic and real vision tasks.
Moment Matching#
Moment matching, in the context of data selection for finetuning, is a crucial technique for controlling variance within a low-dimensional subspace. It ensures that the selected subset of data accurately represents the characteristics of the original dataset, focusing on preserving key statistical moments. This approach is especially valuable when dealing with high-dimensional data, where standard variance minimization alone is insufficient for achieving optimal generalization. By focusing on moment matching in a lower-dimensional space, the method addresses the computational challenges posed by high dimensionality while effectively reducing variance, contributing to faster and more provable finetuning. The process, combined with gradient sketching for subspace identification, offers a scalable and theoretically sound data selection method for improved model performance in deep learning applications.
SkMM Algorithm#
The Sketchy Moment Matching (SkMM) algorithm is a novel approach to data selection for efficient finetuning of deep learning models. It cleverly addresses the variance-bias tradeoff inherent in high-dimensional settings, a critical challenge in modern deep learning where the number of parameters often exceeds the amount of available data. SkMM operates in two stages: first, gradient sketching identifies an informative low-dimensional subspace that captures the essential model behavior for the downstream task. Second, moment matching within this subspace selects a subset of data that minimizes the variance while maintaining a low bias, achieving a crucial balance. This two-stage process is computationally efficient and benefits from theoretical guarantees, ensuring the selection procedure preserves fast-rate generalization. The algorithm’s theoretical foundation provides insights into its efficacy and robustness, supported by empirical results demonstrating its effectiveness in real-world vision tasks, exceeding the performance of traditional methods. Therefore, SkMM presents a significant advancement in the field of data-efficient deep learning, particularly for finetuning.
Future Directions#
Future research could explore extending the coreset selection method to other finetuning settings beyond linear probing. Investigating the impact of different sketching methods and their theoretical properties on generalization performance would be valuable. Further research could also focus on developing more efficient moment matching techniques. The proposed method’s effectiveness on various downstream tasks and different model architectures should be evaluated more extensively. Addressing the computational cost of gradient sketching for extremely large datasets or models is crucial. Theoretical work could also delve deeper into the variance-bias tradeoff, providing a more precise characterization of the optimal balance. Combining the proposed method with other data selection techniques or data augmentation strategies could lead to further improvements in data efficiency.
More visual insights#
More on tables

This table presents the empirical risk (LD(θs)) for different data selection methods on a Gaussian Mixture Model (GMM) dataset with varying sample sizes (n). The risk is measured using ridge regression, and the results are compared to the risk achieved with the full dataset (LD(θ[N]) = 2.95e-3). The table shows how different methods, including uniform sampling, k-center, adaptive sampling, leverage score sampling, and the proposed SkMM method, perform in terms of risk reduction at different sample sizes. The standard deviation across 8 random seeds is reported for the sampling methods.

This table presents the Mean Absolute Error (MAE) results on the UTKFace dataset for age estimation. Different data selection methods were compared using a linear regressor trained on top of CLIP’s pre-trained features (ViT-B/32). The MAE is a measure of the average absolute difference between the predicted and actual ages. Lower MAE values indicate better performance. The table shows MAE values for various coreset sizes (number of selected data points), demonstrating the effectiveness of each data selection method at different data scales.
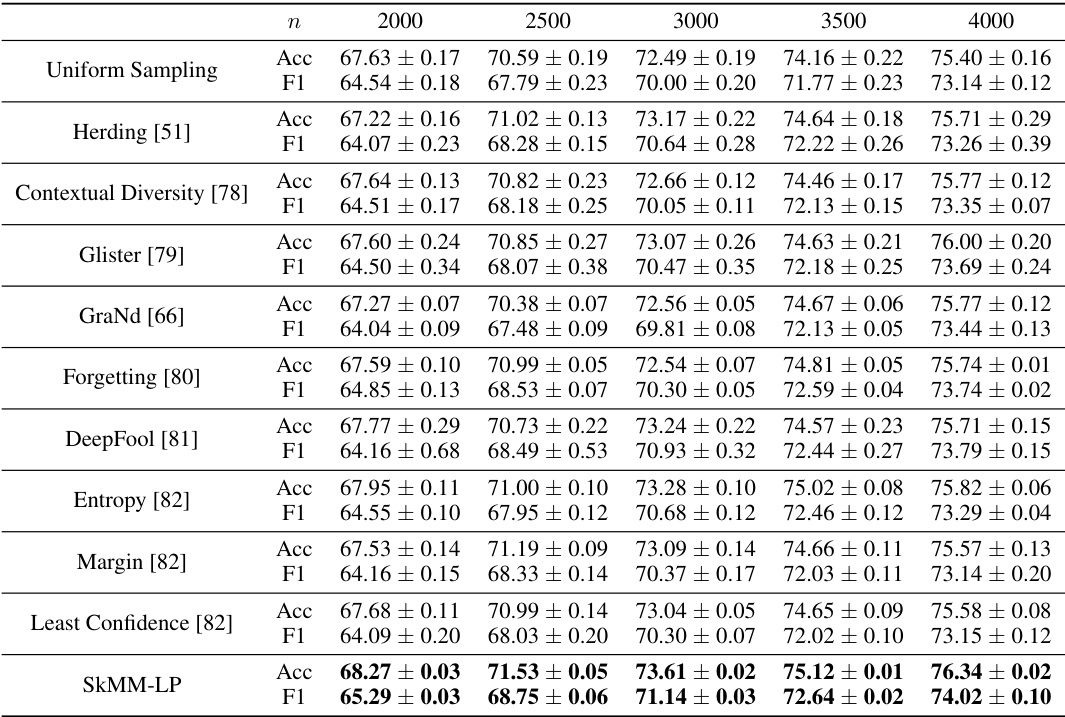
This table presents the accuracy and F1 scores achieved by different data selection methods on the Stanford Cars dataset using linear probing over CLIP features. The results show the performance of various methods including uniform sampling, herding, contextual diversity, Glister, GraNd, forgetting, DeepFool, entropy, margin, least confidence, and the proposed SkMM method. The performance is evaluated for different subset sizes (n) of the dataset.
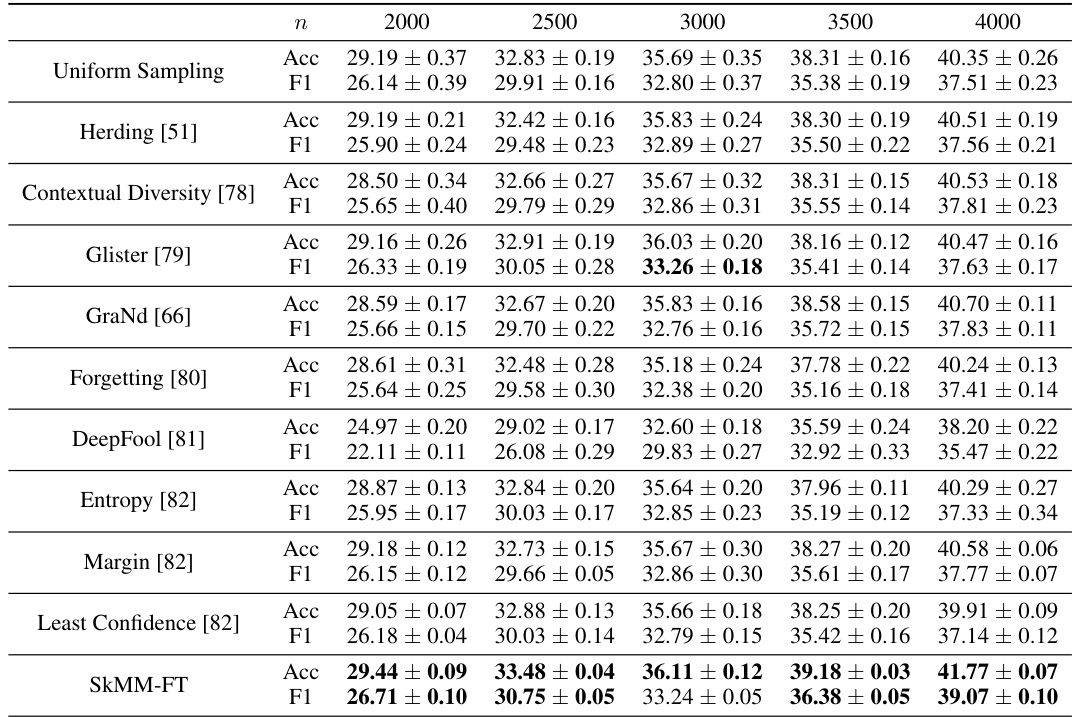
This table presents the accuracy and F1 scores achieved by different data selection methods for linear probing (LP) on the Stanford Cars dataset using CLIP. The results are shown for various coreset sizes (n), demonstrating the performance of SkMM in comparison to other methods like Uniform Sampling, Herding, Contextual Diversity, Glister, GraNd, Forgetting, DeepFool, Entropy, Margin, and Least Confidence.
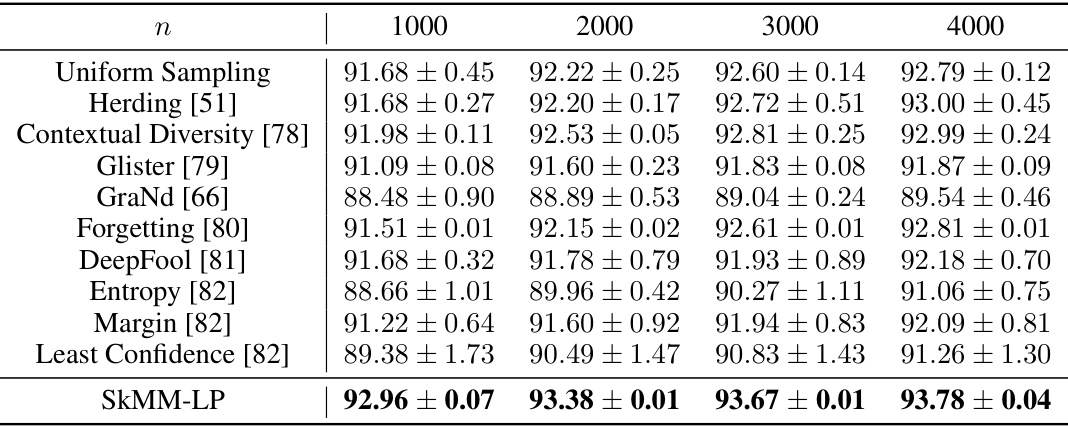
This table presents the results of linear probing (LP) experiments on the Stanford Cars dataset using CLIP. It compares the accuracy and F1 score achieved by SkMM-LP against several baseline data selection methods (Uniform Sampling, Herding, Contextual Diversity, Glister, GraNd, Forgetting, DeepFool, Entropy, Margin, Least Confidence) for different coreset sizes (n). The results highlight the performance of SkMM-LP, particularly in lower coreset sizes.
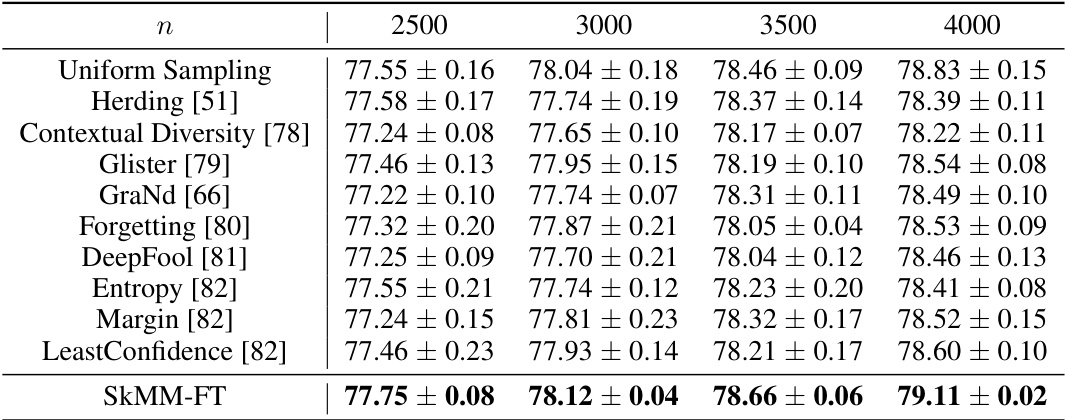
This table presents the Mean Absolute Error (MAE) results for age estimation on the UTKFace dataset using a linear regressor on top of CLIP features. Different data selection methods are compared at various coreset sizes (the number of data points used for training the regressor). Lower MAE values indicate better performance. The best performing method for each coreset size is highlighted in bold.
Full paper#