Policy Aggregation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on AI alignment and multi-agent systems. It bridges the gap between social choice theory and reinforcement learning, offering novel and efficient methods for aggregating diverse preferences into a collective policy. This opens new avenues for developing fairer and more robust AI systems that better align with societal values. The computational methods introduced are also highly valuable for practical applications.

Visual Insights

#

This figure compares the performance of various policy aggregation rules (max-quantile, Borda, a-approval, egalitarian, and utilitarian) across two different scenarios. Each bar represents an agent’s normalized expected return, sorted within each rule. The scenarios differ in agent preferences and the number of agents, allowing for a comparison of the fairness and efficiency of the different rules under varying conditions. Error bars indicate the standard error of the mean.

This table compares the performance of different policy aggregation methods (egalitarian, utilitarian, 80%-approvals, 90%-approvals, Borda, max-quantile) across two different experimental scenarios. The scenarios differ in the number of agents and how those agents value the warehouses (symmetric vs. asymmetric valuations). The table presents the Gini index and Nash welfare for each policy and scenario, summarizing the fairness and economic efficiency of the policies generated by each method. The Gini index measures inequality in the distribution of returns across agents (lower is better), while Nash welfare represents the geometric mean of individual returns (higher is better). The mean and standard error of the metrics are reported.

In-depth insights

#

Policy Voting

#

Policy voting, in the context of AI value alignment, presents a novel approach to aggregating diverse preferences within a multi-agent system. Instead of relying solely on reward functions, which can be susceptible to manipulation and lack a universal scale, policy voting leverages the volumetric interpretation of the state-action occupancy polytope. This framework translates ordinal preferences over policies into volumes within this polytope, enabling the application of various social choice methods, such as approval voting and Borda count. Computational tractability is a key consideration, as direct application of these methods can be computationally expensive; hence, alternative methods are explored. This approach offers the significant advantage of invariance to affine transformations of reward functions, addressing a crucial limitation of utilitarian approaches. The volumetric interpretation provides a robust and efficient method for aggregating diverse preferences to achieve a collective policy that balances individual values and promotes fairness.

Volumetric Fairness

#

Volumetric fairness offers a novel approach to evaluating and achieving fairness in multi-agent reinforcement learning by leveraging the geometry of the state-action occupancy polytope. Instead of relying on traditional methods that often involve complex utility comparisons and interpersonal utility comparisons, volumetric fairness directly assesses fairness based on the volume of the policy space. This approach provides a principled way to define fairness, moving away from potentially arbitrary thresholding or averaging techniques. Furthermore, it enables the development of computationally efficient algorithms for discovering fair policies. By measuring the size of policy subsets preferred by coalitions of agents, the method offers a more intuitive and robust measure of fairness, addressing limitations inherent in discrete preference aggregation. The results from using volumetric interpretations of fairness concepts like the proportional veto core and quantile fairness show promise in obtaining fairer outcomes compared to more traditional welfare-based approaches. However, further investigation into its limitations and scalability in complex settings would enhance its practical applications.

Algorithmic Limits

#

An analysis of Algorithmic Limits in a research paper would explore the inherent constraints and boundaries of algorithms. This involves examining computational complexity, focusing on issues like NP-hardness where finding optimal solutions becomes computationally infeasible as the problem size grows. Further considerations include the limitations of data, such as bias, noise, and incompleteness, which directly impact an algorithm’s accuracy and reliability. Approximation algorithms and heuristics, while often necessary, introduce trade-offs between solution quality and efficiency. The discussion would also address the inherent challenges in modeling complex systems using algorithms, focusing on the gap between abstract models and real-world scenarios. Ethical considerations, such as fairness, accountability, and transparency, are crucial when considering the limits of algorithmic decision-making, highlighting the need for careful design and deployment strategies that address societal impact.

Occupancy Polytope

#

The concept of an “Occupancy Polytope” in the context of multi-objective Markov decision processes (MOMDPs) offers a novel geometric perspective on policy aggregation. It elegantly transforms the problem of combining diverse agent preferences into a volumetric optimization within a well-defined space. Each point in the polytope represents a stochastic policy, characterized by the frequency of visits to various state-action pairs. This volumetric interpretation allows for a natural translation of social choice mechanisms, traditionally designed for discrete settings, into the continuous space of policies. The volume of subsets within the polytope directly reflects the ordinal preferences of agents, enabling the application of voting rules like Borda count and fairness notions such as proportional veto core and quantile fairness. This framework offers significant advantages: invariance to affine transformations of rewards, addressing a critical limitation of reward-based aggregation, and computational tractability, as demonstrated by proposed algorithms leveraging the polytope’s structure. However, computational complexity remains a challenge for certain voting rules, necessitating the use of approximation techniques like Mixed Integer Linear Programming. The framework’s ability to seamlessly integrate fairness considerations and handle the continuous nature of MOMDPs is a substantial theoretical contribution with potential for practical applications in AI value alignment.**

Future Extensions

#

Future research directions stemming from this work could explore several promising avenues. Extending the theoretical framework to encompass more complex settings, such as continuous state and action spaces or online reinforcement learning scenarios, would enhance the applicability of the proposed methods. Investigating the strategic behavior of agents within the policy aggregation process is crucial; addressing potential manipulation is key for real-world deployment. Furthermore, developing more efficient algorithms for policy aggregation, particularly for voting-based rules, will allow scaling to larger problems with many agents and alternatives. Finally, a deeper exploration of different fairness criteria beyond those considered could provide a more nuanced understanding of the trade-offs involved in aligning AI systems with diverse human values.

More visual insights

#

More on figures

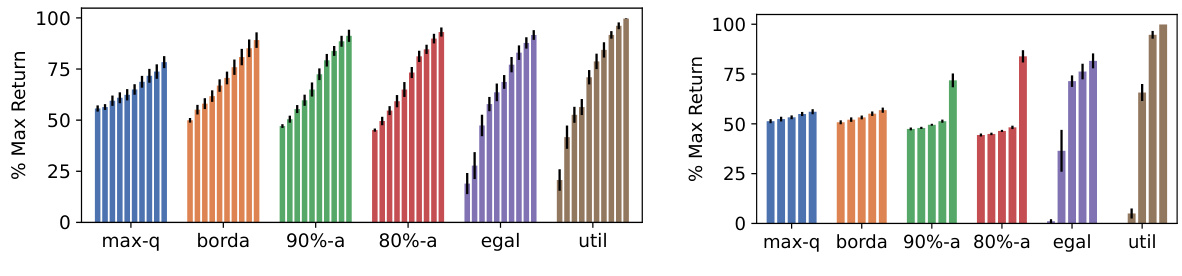
This figure compares the performance of different policy aggregation rules (max-quantile, Borda count, a-approval (90% and 80%), egalitarian, and utilitarian) across two scenarios. Each bar represents an agent’s normalized expected return, sorted within each rule from lowest to highest. The error bars indicate the standard error of the mean, showing variability across multiple runs of the experiments. The scenarios differ in how many agents there are and how many warehouses each agent values, showing how the rules perform under different conditions and group sizes.

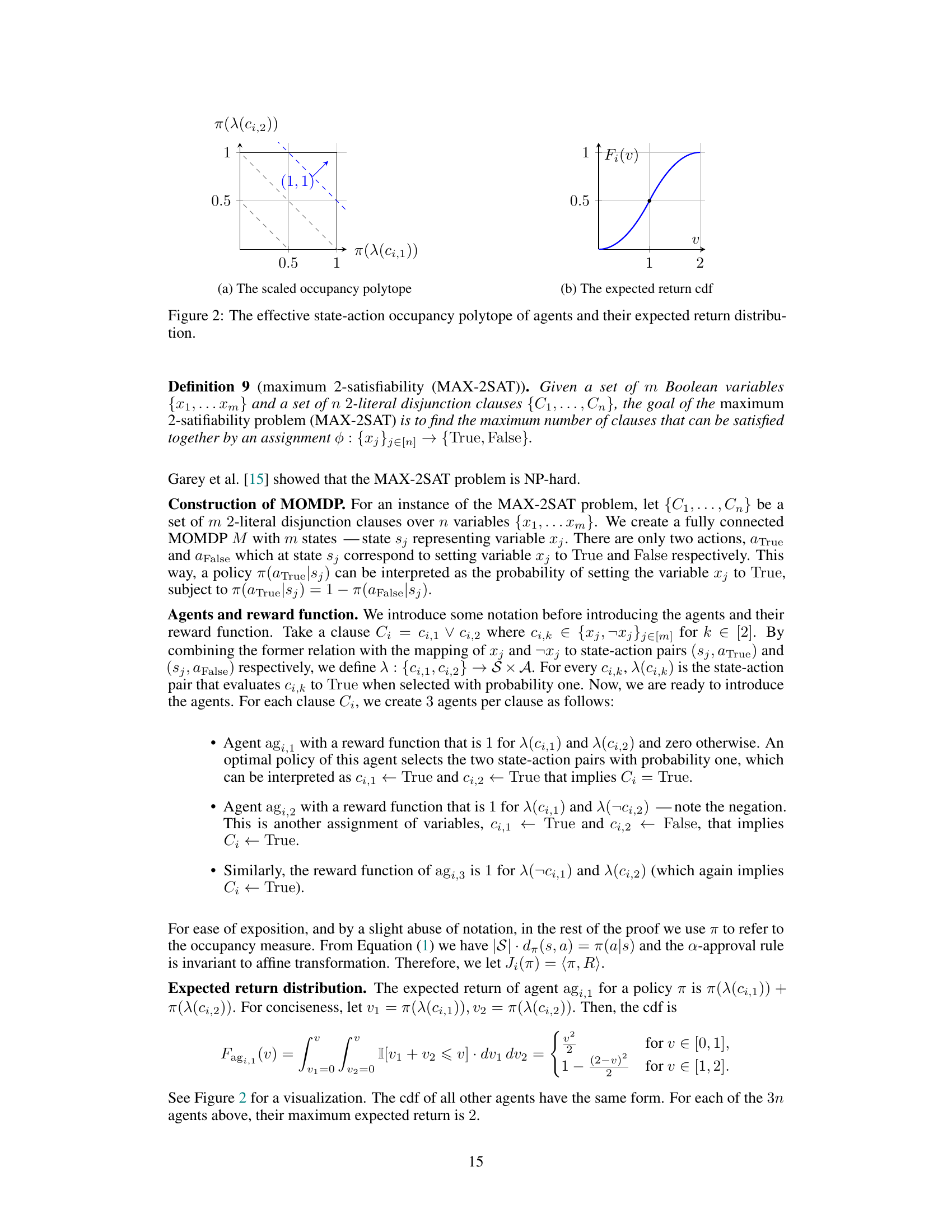
The figure shows the effective state-action occupancy polytope (left) and the expected return cumulative distribution function (right) for agents in the MAX-2SAT reduction. The occupancy polytope is a square with vertices (0,0), (1,0), (1,1), (0,1). The dashed lines represent the constraints v1 + v2 ≥ 3/2 for the a-approval with α ∈ (7/8,1]. The point (1,1) represents the assignment that satisfies both literals.

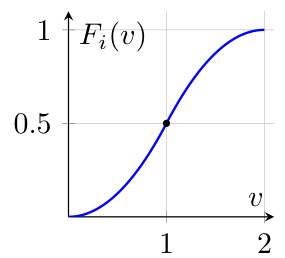
The figure shows two subfigures. Subfigure (a) shows the scaled occupancy polytope and the optimal policies for three agents. Subfigure (b) shows the expected return cumulative distribution function (CDF) of an agent, which is used to determine the fraction of policies that agent prefers.

Full paper

#