↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Predicting the ground state properties of quantum systems is vital for understanding materials and designing quantum computers, but it’s computationally extremely hard. Existing machine learning (ML) methods showed promise but required a sample size that scaled with system size. This is impractical for large systems. The paper addresses this critical scalability problem.
The paper introduces two novel ML approaches to tackle the problem: a modified ML model requiring prior knowledge of the property of interest that achieves constant sample complexity, and a deep neural network model which does not require such prior knowledge, but needs training data sampled from a distribution that satisfies some mild assumptions. Both methods are backed by rigorous theoretical guarantees. Experiments on systems up to 45 qubits demonstrate significant improvements over previous methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers provably efficient machine learning algorithms for predicting quantum many-body ground state properties. This addresses a fundamental problem in physics, which has significant implications for materials science and quantum computing research. The constant sample complexity achieved is a major breakthrough, making the approach practical for large systems.
Visual Insights#
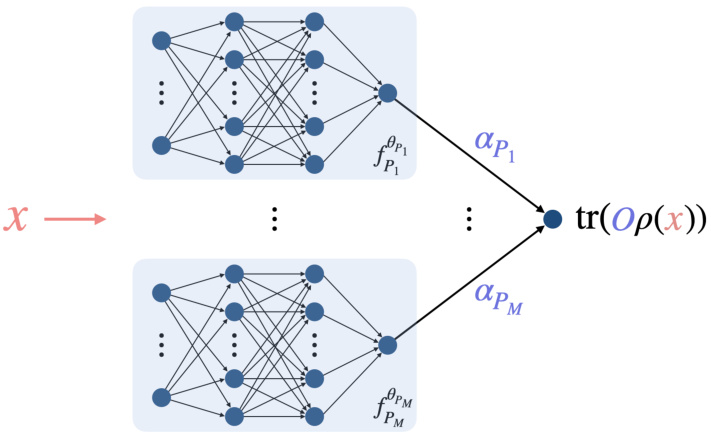
This figure illustrates the deep neural network model used for predicting ground state properties. It consists of multiple local neural network models, each predicting the contribution of a specific Pauli operator to the ground state property. The final output is a weighted sum of these local predictions, where the weights are trainable parameters. The model leverages the geometric structure of the Hamiltonian to improve efficiency.
In-depth insights#
Constant Sample Complexity#
The concept of ‘Constant Sample Complexity’ signifies a significant breakthrough in machine learning, especially within the context of quantum many-body physics. Traditional approaches to learning ground state properties often necessitate a sample size that scales with the system size, rendering them impractical for large systems. This work’s groundbreaking contribution lies in demonstrating algorithms that achieve constant sample complexity, independent of system size. This implies that the number of data points required for accurate prediction remains constant, regardless of how large the quantum system is, making the approach scalable and applicable to realistic, large-scale problems. Two key approaches are introduced: a modified version of an existing algorithm, requiring prior knowledge of the property of interest, and a novel deep neural network model capable of learning even without this prior knowledge. Rigorous theoretical guarantees accompany the proposed algorithms, providing a solid foundation for their practical application and demonstrating the effectiveness of deep learning in tackling complex quantum problems. The constant sample complexity addresses a critical bottleneck in previous approaches, thereby significantly improving the efficiency and feasibility of machine learning techniques for studying quantum systems.
Deep Learning Models#
Deep learning models offer a powerful approach to tackling complex problems in various fields, including scientific research. Their ability to automatically learn intricate patterns from data makes them particularly well-suited for tasks where traditional methods struggle. In the context of quantum many-body physics, deep learning’s capacity to capture high-dimensional relationships between system parameters and ground state properties is invaluable. However, the use of deep learning models is not without challenges. Rigorous theoretical guarantees on their performance are often lacking, a significant hurdle that needs to be addressed for widespread adoption in scientific domains. Despite this, empirical results often show promising results. Successfully training deep learning models requires significant computational resources, potentially limiting their accessibility. Future research should focus on developing models with both high predictive power and robust theoretical justification, while also addressing computational efficiency.
Geometric Locality#
Geometric locality, in the context of quantum many-body systems, is a crucial concept that significantly impacts the efficiency and feasibility of machine learning (ML) based ground state prediction. It posits that the interactions between quantum particles are limited in range and can be described by local Hamiltonian terms. This constraint allows the development of algorithms that scale favorably, as opposed to those dealing with arbitrary long-range interactions. Exploiting geometric locality facilitates a reduction in the dimensionality of the problem, enables efficient feature mapping, and allows the use of simpler models that still achieve high accuracy. While many ML approaches to quantum problems neglect this aspect, rigorous theoretical guarantees in predicting ground state properties, as presented in this work, often rely on the assumption of geometric locality, showcasing its importance in achieving provably efficient algorithms.
Numerical Experiments#
A thorough analysis of the ‘Numerical Experiments’ section would involve examining the types of experiments conducted, the metrics used to evaluate performance, and the interpretation of the results. It’s crucial to assess whether the experiments sufficiently validate the claims made in the paper. Were the experiments designed to address potential confounding factors? A key aspect would be evaluating the statistical significance of the findings; were appropriate error bars or significance tests included? The computational resources used should be carefully considered, and the details should be provided to ensure reproducibility. Finally, a critical analysis requires examining the data visualization techniques; did the plots effectively communicate the results? Were there any limitations in the experimental setup that should be considered?
Future Directions#
The “Future Directions” section of this research paper would ideally explore extending the constant sample complexity results to a broader range of quantum systems. Addressing limitations imposed by the geometric locality assumption is crucial, potentially by investigating alternative ML model architectures or feature engineering techniques that can capture non-local correlations. Investigating lower bounds on sample complexity would strengthen the theoretical contribution, offering insights into the fundamental limits of the proposed approach. Finally, exploring applications beyond ground state property prediction, such as learning thermal states or simulating quantum dynamics with constant sample complexity, would significantly expand the scope and impact of this work.
More visual insights#
More on figures

This figure presents the results of numerical experiments comparing the performance of the proposed deep learning model to a previous regression model. The left panel compares the RMSE prediction error for both methods with a fixed training set size and local neighborhood size. The center panel shows how the deep learning model scales with different training set sizes and local neighborhood sizes. The right panel shows the relationship between the neural network’s training error and the magnitude of its parameters, demonstrating that the assumptions of Theorem 5 are satisfied.

This figure shows a comparison between two sets of points in a 2D space. The blue circles represent points sampled from a uniform distribution using a Sobol sequence, a type of low-discrepancy sequence. The orange triangles depict points generated using the same Sobol sequence but transformed by the CDF of a standard normal distribution. This transformation alters the distribution of points, making them more concentrated around the center of the space and less dense near the boundaries. This transformation is to illustrate how to generate low-discrepancy sequences for arbitrary distributions.
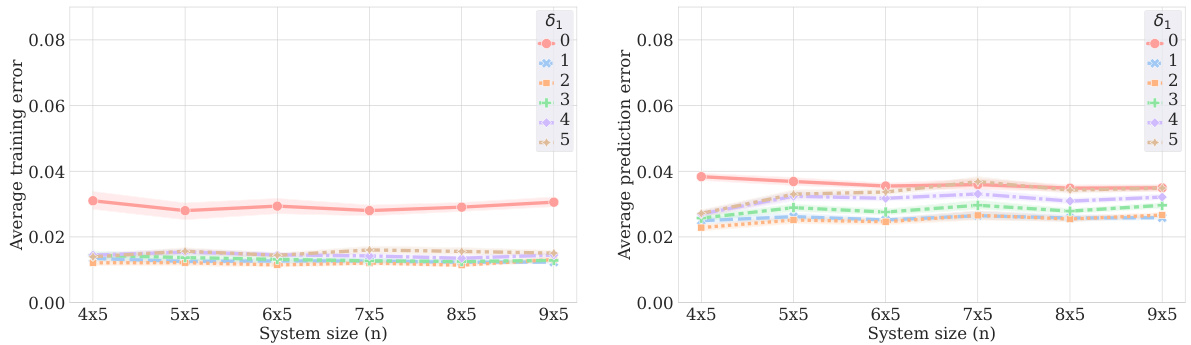
This figure presents a comparison of the deep learning model’s performance against previous methods, its scaling behavior with training size, and an analysis of the neural network’s weights and training error. The left panel compares the deep learning model with the regression model from [2]. The center panel shows how prediction error scales with the training set size. The right panel displays the neural network weights and training error, confirming the assumptions of Theorem 5.

This figure presents a comparison of the proposed deep learning model with previous methods in terms of prediction error (RMSE), investigating the scaling of prediction error with respect to training set size and the impact of the local neighborhood size, and examining the neural network weights and training error to validate the assumptions made in Theorem 5. The left panel shows a comparison of the deep learning model and a regression model from a prior study for different training data types and neighborhood size values. The middle panel shows how prediction error changes as the training set size increases for different values of the neighborhood parameter. The right panel examines the relationship between training error and the norm of the neural network weights, providing visual evidence for the fulfillment of the assumption in Theorem 5.
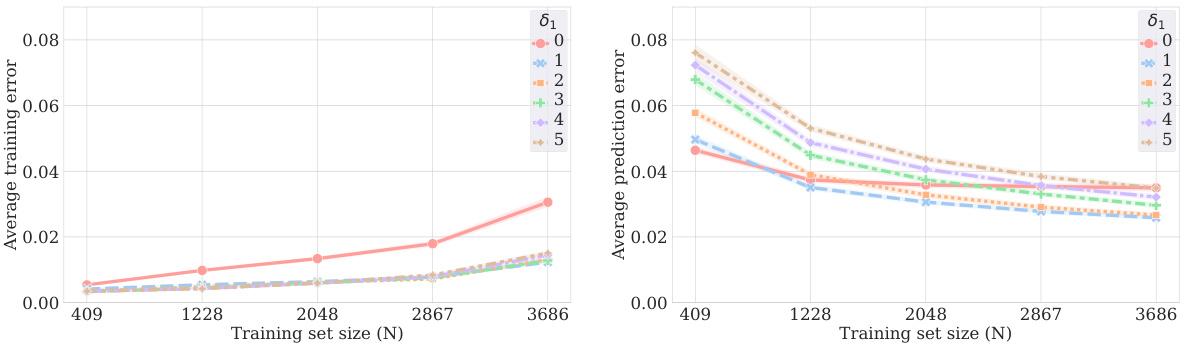
This figure presents a comparison of the deep learning model’s performance against a regression model, illustrating the scaling of prediction error with training set size and the relationship between training error, parameter norm and the δ₁ parameter. The left panel compares the RMSE of both models for different data distributions and a fixed training set size; the center panel examines prediction error for varying training sizes and δ₁ values using LDS data, and the right panel visually demonstrates the relationship between training error and the l₁-norm of the neural network’s weights.

This figure presents a comparison of the deep learning model’s performance against a regression model from a previous study [2] for predicting ground state properties of quantum systems. The left panel shows the root mean square error (RMSE) for various system sizes, using both low-discrepancy sequences (LDS) and randomly generated data. The center panel demonstrates how the RMSE scales with the size of the training dataset for various choices of a parameter (δ₁). Finally, the right panel shows the training error and the magnitude of the weights in the neural network, corroborating that the assumptions for the theoretical guarantee hold.
Full paper#



















