↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Accurately determining the spatial distribution of brain tumor cells is crucial for effective treatment planning, but medical imaging alone is insufficient. Existing physics-based models often over-constrain the solution space, while data-driven approaches lack biological insights. This research addresses this limitation by proposing a novel method that combines the strengths of both. The core challenge lies in the difficulty of estimating the spatial distribution of tumor cells, especially in infiltrative tumors like glioblastoma, where low-concentration tumor cells remain undetectable. The incomplete tumor cell distribution also makes it difficult to create appropriate training data for machine learning models.
The researchers introduce a new method that integrates data-driven and physics-based cost functions on a dynamic discrete mesh, providing flexibility and enhanced integration of patient data. This approach effectively models complex biomechanical behaviors and quantifies the adherence of learned spatiotemporal distributions to growth and elasticity equations. The method shows improved coverage of tumor recurrence areas compared to existing methods using real-world data. The ability to learn the initial condition and integrate additional imaging modalities, such as PET scans, further enhances the method’s performance.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel hybrid approach to brain tumor localization, combining data-driven methods with physics-based constraints. This addresses a critical challenge in oncology, where accurate tumor boundary delineation is crucial for effective treatment planning. The improved accuracy and coverage of tumor recurrence areas demonstrated in this study have significant implications for improving glioblastoma treatment and patient outcomes. The use of a dynamic discrete mesh and physics-regularization offers greater flexibility and improved integration of patient data compared to existing models. The method’s ability to learn the complex unknown initial condition, which includes not just the pathology’s origin but also the brain tissue’s initial state, is also a significant contribution. This approach could inspire further research into hybrid methods for other medical image analysis tasks, particularly those involving complex biological processes.
Visual Insights#
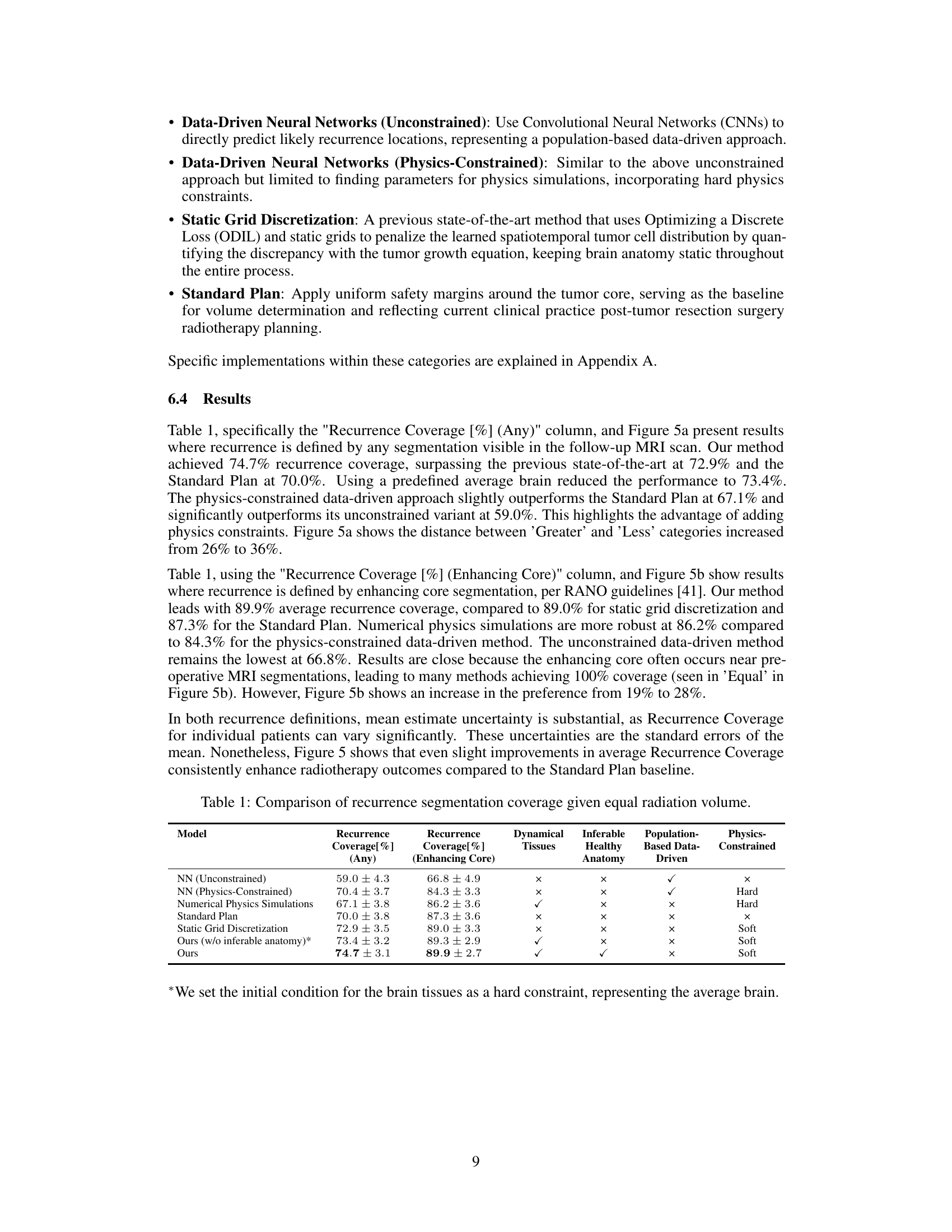
This figure provides a visual overview of the proposed method. Panel (a) shows the input data: 3D MRI and PET scans of a glioblastoma patient. Panel (b) details the preprocessed data used, including brain tissue maps derived from the scans, and a tumor segmentation. Panel (c) illustrates the core of the method: physics-regularized learning of spatiotemporal distributions of tumor cells and brain tissues. The method uses a loss function that incorporates physical assumptions and integrates data to learn the spatial tumor cell distribution and brain anatomy. Panel (d) presents the method’s output: the inferred initial healthy anatomy, spatial tumor cell distribution, and system identification parameters. This output can be used for radiotherapy planning.
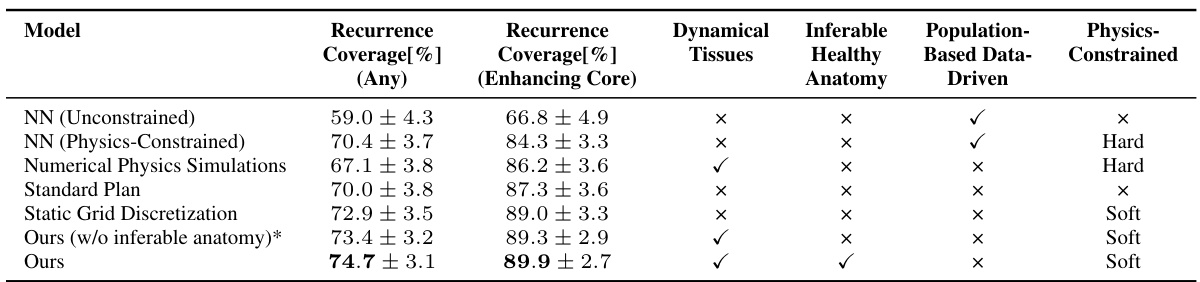
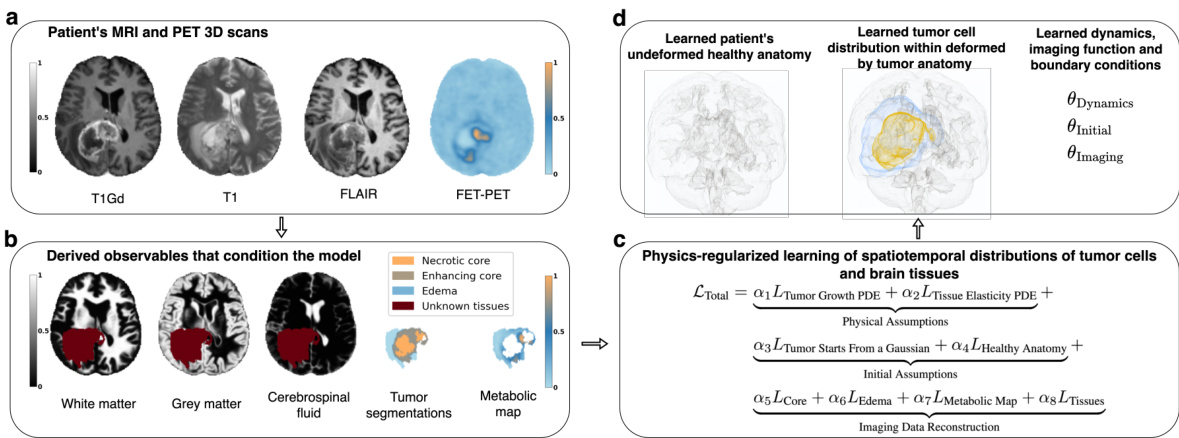
This table compares the performance of different models in predicting tumor recurrence, using two metrics: Recurrence Coverage (Any) and Recurrence Coverage (Enhancing Core). The models are categorized into data-driven (constrained and unconstrained), physics-based, and a standard clinical approach. The table also indicates whether each model utilizes dynamical tissues, infers healthy anatomy, and incorporates population-based data or physics constraints. The results demonstrate the superiority of the proposed method in accurately identifying recurrence areas.
In-depth insights#
Physics-Informed Learning#
Physics-informed learning (PIL) blends physical principles with data-driven approaches, creating powerful hybrid models. PIL leverages physical laws, often expressed as partial differential equations (PDEs), to guide and regularize the learning process. This results in models that are more accurate, generalizable, and interpretable than purely data-driven counterparts, particularly when training data is limited. A key advantage of PIL is its ability to incorporate prior knowledge about the underlying physical system, which can significantly improve model performance and reduce the need for extensive data. However, successful PIL implementations require careful consideration of both the physical model and the machine learning algorithm. Choosing appropriate PDEs and discretization techniques, as well as handling complex geometries and boundary conditions, are crucial steps. The balance between data fidelity and adherence to physical laws is also a critical aspect of PIL, often requiring careful tuning of hyperparameters or the development of novel loss functions. Despite these challenges, PIL offers a promising path towards developing sophisticated and robust models in various scientific and engineering domains.
Hybrid Model Fusion#
A hybrid model fusion approach in medical image analysis, particularly for brain tumor localization, could significantly improve diagnostic accuracy and treatment planning. Combining data-driven models’ flexibility with physics-based models’ adherence to biological principles is crucial. Data-driven models, like deep learning networks, excel at identifying complex patterns in imaging data but may lack the underlying biological understanding. Conversely, physics-based models offer this crucial understanding but often struggle with the complexity and variability inherent in real-world patient data. Therefore, a hybrid approach that leverages the strengths of each model type is essential for robust and accurate results. Successful integration might involve a weighted ensemble or a more sophisticated fusion mechanism, possibly incorporating uncertainty quantification from each model to guide the fusion process. The fusion should ideally be tailored to the specific task, considering the relative importance of data-driven and physics-informed information for optimal performance. This strategy promises to generate more reliable and personalized medical diagnoses and treatment plans while mitigating the limitations of individual model types.
Growth & Elasticity#
The concept of growth and elasticity in the context of brain tumor modeling is crucial for accurately representing the complex interplay of biological processes and mechanical forces within the brain tissue. Growth refers to the proliferation and spread of tumor cells, driven by factors like cell division rates and diffusion processes. The study of tumor growth is complicated by the heterogeneous nature of brain tissue, with varying densities and elastic properties influencing the spread of tumor cells. Elasticity in this context refers to the ability of brain tissue to deform and recover its shape under the influence of external forces, including the pressure exerted by a growing tumor. The incorporation of elasticity into models is important because tumor growth generates mechanical stresses that affect the surrounding tissue, potentially altering the tumor’s shape and migratory patterns. A combined model that accounts for both growth and elasticity is vital for creating more accurate and predictive simulations, allowing for more effective treatment planning and potentially personalized medicine approaches. The interaction of these factors determines the tumor’s overall behavior, which can lead to highly unpredictable outcomes. Therefore, understanding these dynamic processes is critical for the development of advanced computational models that can accurately reflect the tumor’s evolution within the brain, thereby informing more informed treatment strategies.
Radiotherapy Planning#
The research explores physics-regularized multi-modal image assimilation for enhanced brain tumor localization, significantly impacting radiotherapy planning. Current radiotherapy relies on a uniform radiation margin around visible tumors, neglecting infiltration patterns and tissue heterogeneity. This study introduces a novel method integrating data-driven and physics-based approaches, allowing for more accurate tumor boundary delineation and improved target volume definition. By incorporating physical models of tumor growth and tissue elasticity, the model achieves superior performance in predicting tumor recurrence areas, leading to more personalized and effective radiotherapy plans. The hybrid approach combining data-driven learning with physical constraints offers greater flexibility and accuracy compared to traditional physics-based or purely data-driven methods. This could lead to improved patient outcomes and reduced side effects by optimizing radiation delivery based on a more precise understanding of the tumor’s spatial distribution and its interaction with surrounding brain tissue.
Limitations & Future#
The research paper’s methodology, while innovative, presents several limitations. The reliance on a multi-resolution grid introduces the risk of inaccuracies at finer resolutions due to the nature of approximation. This needs further investigation for optimal balance between computational cost and accuracy. The soft physics constraints, while allowing flexibility, may not fully capture the complexity of tumor growth and tissue interactions. There is also a need for more robust validation with larger and more diverse datasets to confirm generalizability across various patient characteristics and tumor types. Future work should explore alternative discretization schemes to improve accuracy, particularly in areas of high tumor heterogeneity. Further refinement of the model’s physical parameters and potentially incorporating additional imaging modalities would enhance biological realism. Addressing these limitations and expanding the dataset will improve the clinical translation potential of this promising methodology. Development of clinically validated treatment plans requires further research and integration with clinical workflows.
More visual insights#
More on figures

This figure illustrates the learning process of the proposed method. It shows how initial assumptions, physics-based penalties, and imaging data reconstruction work together to optimize the spatiotemporal distributions of tumor cells and tissues. The initial conditions are set with a symmetric healthy anatomy and an initial tumor distribution modeled as a Gaussian blob. Physics-based penalties enforce consistency between initial and final states according to the governing equations, and imaging data reconstruction ensures that learned distributions are aligned with actual imaging observations, including tumor segmentations and a metabolic map.
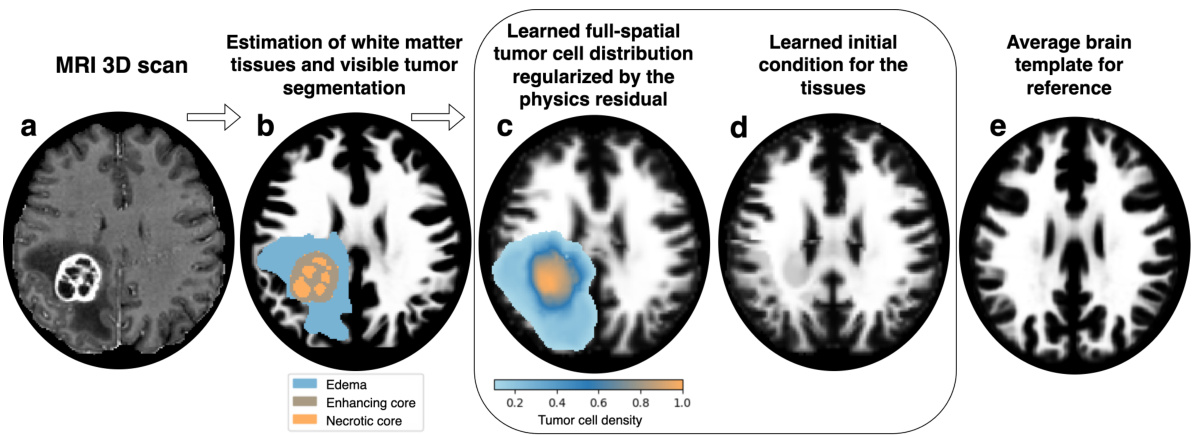
This figure shows the inference process of the proposed method. It starts with the patient’s MRI scan (a), then estimates the white matter tissues and tumor segmentation (b). The method infers the full spatial tumor cell distribution, regularized by the physics residual and aligned with the patient data (c). Then, the method infers the healthy anatomy (d) and finally uses an average brain template for reference (e). The differences between the inferred healthy anatomy and the average brain template highlight potential areas that could affect tumor cell inference.

This figure provides a visual overview of the proposed method. It shows the inputs (3D MRI and PET scans of a glioblastoma patient and pre-processed data), the process of learning the tumor cell distribution and brain anatomy using a physics-informed loss function, and the outputs (initial healthy anatomy, spatial tumor distribution, and system parameters).

This figure compares three different approaches for radiotherapy planning. (a) shows the pre-operative MRI scan with tumor core segmentation. (b) illustrates the standard radiotherapy plan, which uses a 1.5cm margin around the visible tumor. (c) presents the results of the proposed method, showing a learned tumor cell distribution that is used to define a radiotherapy contour with a volume equal to the standard plan. The recurrence coverage is significantly improved by the proposed method (77.00% vs 62.33%).
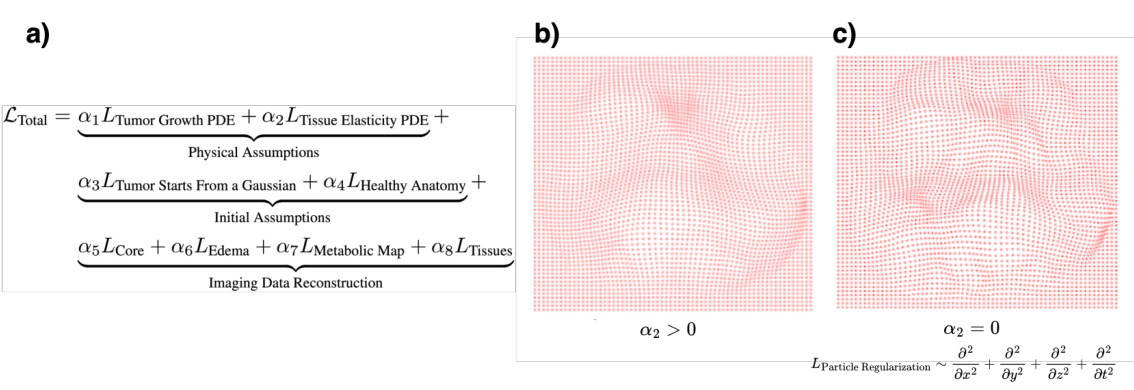
This figure shows the effect of the regularization term (α2) on the deformation of the tissue. Panel (a) shows the total loss function, which includes terms for tumor growth, tissue elasticity, initial conditions, and imaging data reconstruction. Panels (b) and (c) show the deformation of the tissue with (α2 > 0) and without (α2 = 0) the regularization term, respectively. When the regularization term is included, the deformation is more localized and biologically plausible, while without regularization, there are multiple smaller deformations.
More on tables

This table presents the results of a comparison between the proposed method and the Static Grid method on synthetic datasets. The RMSE (Root Mean Square Error) is used to evaluate the performance of both methods in predicting tumor locations. The results are shown for different input types, representing varying levels of information available during training. The results demonstrate that the proposed method achieves a lower RMSE, particularly with more comprehensive input data, highlighting its superior performance in capturing tumor growth and tissue deformation compared to the Static Grid approach.

This table presents the results of statistical significance tests comparing the recurrence coverage achieved by the proposed method against other methods. The Wilcoxon signed-rank test was used, as the data was not normally distributed. The comparison is made for two metrics of recurrence: any recurrence (based on any segmentation in the follow-up MRI) and enhancing core recurrence (based on enhancing core segmentation as per RANO guidelines). The p-values indicate the statistical significance of the differences.
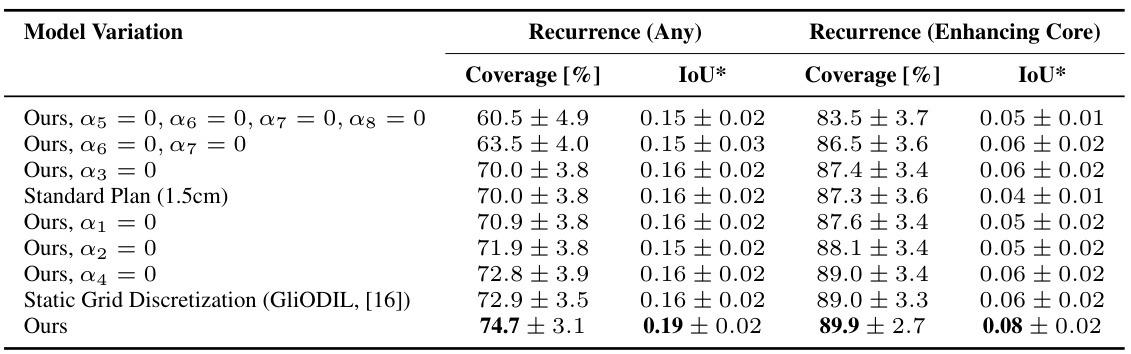
This table presents the results of an ablation study investigating the impact of removing different components of the model’s loss function on the performance metrics: recurrence coverage (any and enhancing core) and Intersection over Union (IoU). It compares the performance of the full model with variations where specific regularization terms (physics-based, initial assumptions, imaging data) are removed. The results show that removing different regularization terms has varying impact on both recurrence coverage and IoU. The full model achieves superior performance than models with any component removed or the standard plan baseline.
This table compares the performance of different models in predicting tumor recurrence areas for radiotherapy planning. The models include several data-driven approaches, physics-based simulations, and a standard clinical approach. Performance is evaluated based on recurrence coverage (percentage of true recurrence areas covered by the predicted target volume) for two different definitions of recurrence (any segmentation and enhancing core). The table highlights the superior performance of the proposed physics-regularized method compared to other methods and the standard clinical practice.

This table lists the Young’s modulus and Poisson’s ratio values used in the hyperelastic modeling of different brain tissues (gray matter, white matter, cerebrospinal fluid) and tumor tissue in the study. These values are crucial parameters for the biomechanical model used in the paper to simulate tumor growth and its interaction with the surrounding brain tissue.
Full paper#