↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning applications rely on learning cluster structures from data. However, often, data is noisy or information sources are unreliable. This paper studies a clustering problem where a learner needs to partition a finite set by querying a faulty oracle (e.g. human workers or experiments that may contain errors). The challenge lies in designing algorithms that can perfectly reconstruct this partition despite the faulty answers. Previous works often assume error-free queries or focus on probabilistic guarantees.
This paper proposes novel algorithms to exactly reconstruct the partition even with errors. They use a game-theoretical framework based on correlation clustering and a Rényi-Ulam style approach. The algorithms achieve optimal query complexity, which is the minimum number of queries needed. Interestingly, the study reveals that the required queries are not symmetric for false-positive and false-negative errors, offering valuable insights for algorithm design and resource management.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on robust and efficient algorithms for clustering problems in the presence of noisy data or unreliable information sources. It provides tight theoretical bounds on query complexity, a novel analytical framework, and optimal algorithms for learning partitions with faulty oracles, which is highly relevant to many real-world applications involving crowdsourcing or noisy experiments.
Visual Insights#

This figure shows the hierarchy of problems discussed in the paper. The simplest problem is learning partitions without errors, which serves as a baseline. From there, three increasingly complex variations are introduced: the l-PL problem (with both false positive and false negative errors), the l-PLFP problem (with only false positive errors), and the l-PLFN problem (with only false negative errors). The weighted l-PL problem is a generalization that incorporates different penalties for false positives and false negatives. The arrows represent the relationship between these problems in terms of algorithmic and lower bound implications. Algorithmic results flow from left to right, meaning that an algorithm for a more complex problem implies an algorithm for simpler ones. Lower bound results, on the other hand, flow from right to left, demonstrating that lower bounds for a simpler problem apply to more complex problems.
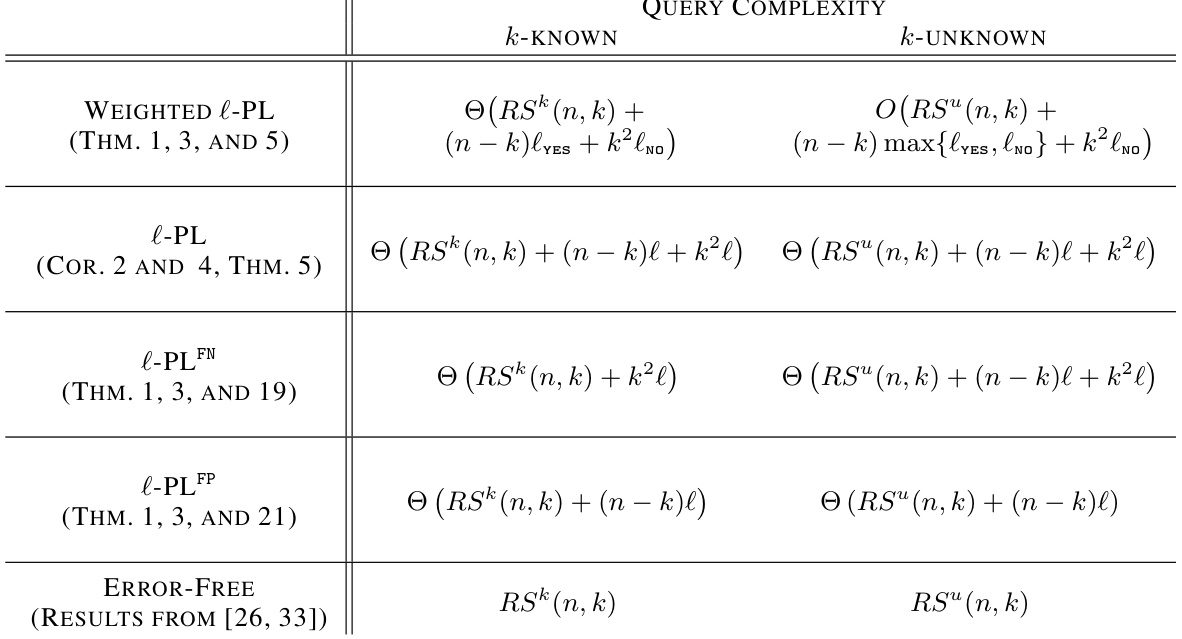
This table summarizes the query complexity results for various partition learning problems with faulty oracles. It shows the complexity for different scenarios: whether the number of clusters (k) is known or unknown, and whether the oracle can have false positives, false negatives, or both. The complexities are expressed in terms of RSk(n,k) and RSu(n,k), representing the complexities in the error-free setting for known and unknown k respectively.
In-depth insights#
Faulty Oracle Models#
Faulty oracle models represent a significant departure from traditional machine learning assumptions, introducing noise and error into the learning process. This approach is particularly valuable when dealing with real-world data sources where perfect information is unavailable, such as in crowdsourcing or biological experiments. By explicitly modeling the presence of errors, faulty oracle models create a more realistic and robust learning framework. The challenge lies in designing algorithms that can effectively learn despite this noise; the core of the problem lies in determining the minimum number of queries and the optimal querying strategy necessary for accurate recovery of the desired structure, even in the presence of a bounded number of faulty responses. Analyzing the effects of different types of errors (false positives vs. false negatives), and their influence on query complexity reveals inherent asymmetries and provides critical insights for developing more effective and efficient learning algorithms in noisy environments. The use of game-theoretic frameworks and correlation clustering techniques are valuable approaches to both analyze and provide a theoretical understanding of the optimal strategies and complexity of these tasks.
Query Complexity#
The research paper delves into the ‘Query Complexity’ of learning partitions using faulty oracles, a problem arising in crowdsourcing and scientific experimentation. Optimal algorithms are designed, and their query complexities are rigorously analyzed. The analysis reveals an inherent asymmetry in the complexity required to handle false positive versus false negative errors from the oracle. Tight lower bounds are proven, demonstrating the optimality of the proposed algorithms. The study leverages connections to correlation clustering and Rényi-Ulam games, providing a novel analytical framework. The results offer significant insights into the fundamental limits of learning with noisy data through queries, highlighting practical implications for designing efficient and robust algorithms in real-world scenarios. The key contribution lies in establishing matching upper and lower bounds on the query complexity for various settings, including those with known and unknown numbers of clusters and different types of oracle errors. This contributes significantly to the understanding of the trade-offs between query cost and error tolerance in partition learning problems.
Algorithmic Robustness#
Algorithmic robustness, in the context of this research paper focusing on learning partitions with faulty oracles, centers on the ability of algorithms to accurately recover the underlying partition despite noisy or erroneous responses from the oracle. The paper investigates the design of algorithms that are not only efficient but also tolerant to a bounded number of incorrect answers, addressing the challenges presented by non-persistent errors. A key aspect is the inherent asymmetry revealed in the query complexity: the algorithms exhibit different complexities depending on whether they are robust against false positive or false negative errors. This highlights the need for carefully designed algorithms that explicitly address the nature and potential impact of oracle errors. The authors explore the theoretical limits of robustness, establishing optimal query complexities in various settings, and provide detailed algorithmic solutions with proven guarantees of exact recovery under the assumption of a bounded number of faulty answers.
Asymmetric Error#
The concept of “Asymmetric Error” in the context of a research paper on learning partitions with faulty oracles highlights a crucial observation: the impact of false positives and false negatives is not equal. The algorithm’s performance is affected differently by each type of error, with the cost of handling them exhibiting an inherent asymmetry. This asymmetry arises from the fundamental nature of the problem: verifying the absence of connections (false negatives) requires significantly more effort than confirming the presence of connections (false positives). False negatives necessitate constructing a large clique of negative responses, which can be computationally expensive. Conversely, false positives only require building a spanning forest, a less demanding process. Understanding this asymmetry is vital for designing efficient and robust algorithms, as strategies optimized for one type of error may be suboptimal or even ineffective when faced with the other. This finding emphasizes the importance of considering the specific error characteristics of the oracle when devising a partition learning strategy and underscores the potential for developing tailored approaches based on these asymmetries.
Future Directions#
The paper’s “Future Directions” section would ideally expand on several key areas. Firstly, tightening the upper and lower bounds for the weighted l-PL problem in the k-unknown setting is crucial. The current bounds leave a gap, and resolving this would provide a more complete theoretical understanding. Secondly, exploring alternative query models beyond same-cluster queries, such as triangle queries, is a significant avenue for future research, potentially leading to more efficient algorithms or applicability in different contexts. Thirdly, investigating algorithms that function without a priori knowledge of lyes (the number of false positive answers) while maintaining exact recovery guarantees, offers an interesting challenge. Finally, extending the error model beyond the adversarial, non-persistent errors currently considered is important. This might involve exploring probabilistic error models or persistent errors, which present new theoretical hurdles and practical applications.
More visual insights#
More on figures

This figure shows the hierarchy of problems studied in the paper, illustrating the relationships between different variants of the l-PL problem (learning partitions with faulty oracles). The problems are arranged in a lattice structure, where arrows indicate implications about the relative difficulty of problems. For example, the weighted l-PL problem is shown as the most general problem, from which the simpler l-PL problem, l-PLFP, and l-PLFN problems can be derived by setting parameters appropriately. The direction of the arrows indicates how algorithmic results (upper bounds) and lower bound results flow through the hierarchy; upper bound results for more general problems usually apply to more specific problems, while lower bound results for more specific problems generally extend to more general problems.
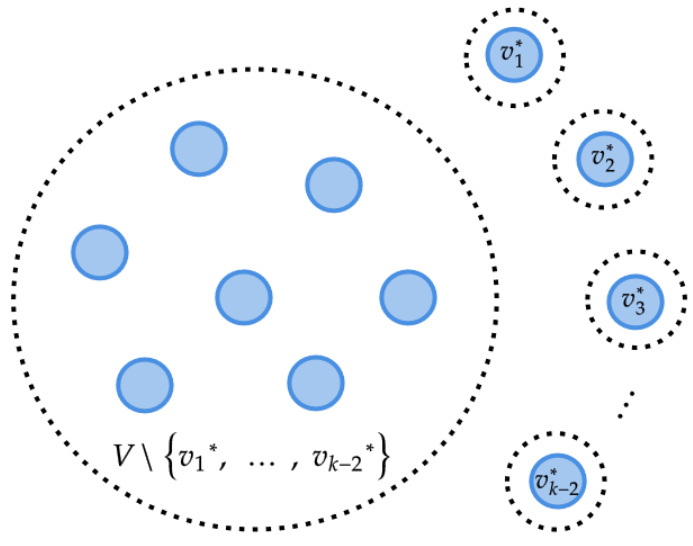
This figure illustrates the (k-1)-partition C* used in the (k-1)-groups responder strategy for the RUCCFP game. The set V is partitioned into k-1 subsets. k-2 elements are each in their own singleton set. The remaining elements form a single set containing the rest of the elements in V.
Full paper#



















