Avoiding Undesired Future with Minimal Cost in Non-Stationary Environments

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on decision-making under uncertainty and non-stationary environments. It provides a novel, efficient, and theoretically-grounded approach to the Avoiding Undesired Future (AUF) problem, a prevalent challenge across numerous domains. Its efficient solution to the AUF problem, particularly its ability to deal with non-stationary dynamics and incorporate cost considerations, opens new avenues for research in reinforcement learning, causal inference, and robust decision-making. The polynomial-time algorithm ensures scalability, making it applicable to real-world problems with large-scale datasets.

Visual Insights

#

This figure shows the concept of rehearsal graphs and how alterations change them. Panel (a) displays the original rehearsal graph, depicting the influence relationships between variables X, Z1, Z2, Z3, and Y1, Y2. Panels (b), (c), and (d) illustrate the alteration graphs resulting from interventions on one or more Z variables. Specifically, the incoming arrows into the altered Z variable(s) are removed, indicating that the influence from other variables is disrupted by the intervention. This showcases how the alteration graphs illustrate the changes in influence relationships after a decision or intervention has been made.

This table shows the average running time in seconds for different algorithms (DDPG, PPO, SAC, QWZ23, MICNS) on two datasets (Market and Bermuda). It compares the efficiency of the proposed AUF-MICNS method (MICNS) with a prior method (QWZ23) and several reinforcement learning algorithms.

In-depth insights

#

AUF in Non-Stationary

#

The concept of “AUF in Non-Stationary” environments presents a significant challenge in machine learning. Non-stationarity, where the underlying data distribution changes over time, directly undermines the effectiveness of traditional Avoiding Undesired Future (AUF) methods. These methods often rely on stable relationships between variables, which are disrupted in non-stationary settings. The core challenge lies in adapting to these dynamic changes while still achieving the primary goal of preventing undesirable future events. Robust methods capable of effectively tracking and updating the evolving relationships between variables are crucial to solve this problem. This necessitates techniques that can handle concept drift and maintain up-to-date models of dynamic influence relations to prevent the occurrence of undesired outcomes with minimal cost. This is particularly important in real-world applications where the cost associated with decision actions is a critical consideration. Therefore, developing efficient algorithms capable of addressing the AUF problem in the presence of non-stationarity is an important and complex problem that requires both theoretical and practical advancements to make effective decisions in real-world dynamic systems.

Sequential Influence

#

The concept of “Sequential Influence” in a non-stationary environment suggests a dynamic interplay where influence relationships between variables evolve over time. This necessitates a method that can effectively track and update these changing relationships. A key challenge lies in the limited data available in each time step, making robust estimation difficult. The research likely addresses this via a sequential algorithm that incorporates new data incrementally, perhaps using an online learning approach or a recursive Bayesian update. Careful consideration of the cost associated with decision actions is also critical in a non-stationary setting because costs themselves might fluctuate. The optimal approach would balance the cost of action against the potential for avoiding an undesired outcome, likely resulting in a cost-sensitive decision-making framework. The theoretical analysis likely involves proving guarantees on the accuracy of the influence relation estimation over time, potentially establishing bounds on the error or demonstrating convergence to the true underlying relations. The framework’s strength would rest in its ability to handle non-stationarity, enabling its application in dynamic real-world problems where influence relationships are inherently volatile.

AUF-MICNS Algorithm

#

The AUF-MICNS algorithm, designed for the Avoiding Undesired Future (AUF) problem in non-stationary environments, presents a novel approach to sequential decision-making. It addresses the limitations of existing methods by dynamically updating estimates of influence relations among variables. This dynamic updating is crucial because real-world environments rarely remain stationary, and influence relationships can shift over time. The algorithm incorporates a cost function, allowing for the selection of actions that minimize cost while effectively preventing undesired outcomes. A key contribution is the formulation of the AUF problem as a convex quadratically constrained quadratic program (QCQP), enabling efficient solutions even with multiple variables. This contrasts with previous approaches that were often computationally intractable for high-dimensional problems. The use of an online-ensemble-based sequential algorithm provides robustness to uncertainty in the degree of non-stationarity. By leveraging these components, AUF-MICNS offers an efficient and effective solution for making optimal decisions in complex, dynamic systems where both cost and outcome are crucial considerations.

Theoretical Guarantees

#

A thorough theoretical analysis is crucial for establishing the reliability and effectiveness of any machine learning model, especially in complex, non-stationary environments. Theoretical guarantees provide formal mathematical bounds on the performance of the proposed method, such as error bounds in parameter estimation or probability bounds in achieving the desired outcome. For the ‘Avoiding Undesired Future (AUF)’ problem, strong theoretical guarantees ensure the algorithm’s robustness to environmental changes and the reliability of its decision-making process. Specifically, proving that the estimated influence relations converge to the true relations within a bounded error, and that the suggested decisions lead to the desired outcome with a probability exceeding a certain threshold are essential. These guarantees not only validate the algorithm’s efficacy but also build confidence in its applications, particularly in high-stakes scenarios where reliability is paramount. The theoretical analysis should address the algorithm’s convergence properties, computational complexity, and assumptions made during its formulation. By rigorously proving that the algorithm satisfies the required properties, we can provide assurance that the decisions suggested by the model will achieve the desired outcome. It is worth mentioning the importance of the underlying assumptions, as it determines the scope and generalizability of the theoretical guarantees. A discussion on limitations and potential directions for future research, such as relaxation of assumptions or handling more complex scenarios, will further strengthen the theoretical analysis. The use of convex optimization is a major strength of the paper as it directly contributes towards obtaining polynomial time algorithmic solutions. Thus, the presented theoretical analysis must be comprehensive, rigorous, and well-supported by proofs.

Future of AUF Research

#

The future of Avoiding Undesired Future (AUF) research is bright, given its practical relevance and the potential for significant advancements. Addressing non-stationary environments is crucial; current methods struggle with dynamic influence relations, thus, robust online learning techniques and adaptive models are needed. Incorporating cost into the decision-making process is also vital. Moving beyond simplistic cost functions to reflect the real-world complexities of decision-making will refine and improve decision quality. Expanding beyond linear Gaussian cases is key to tackling real-world problems. Methods capable of handling non-linear relationships and more complex data distributions will broaden the applicability of AUF. Finally, integrating explainability and human-in-the-loop elements is needed for trust and effective collaboration between algorithms and decision-makers. By addressing these challenges, AUF research can deliver more effective, efficient, and reliable decision support systems across various fields.

More visual insights

#

More on figures

This figure shows an example of how to estimate the probability region P with an expected probability of τ=0.9. The left panel shows samples from the probability distribution F_Yt of Yt. The right panel shows the estimated probability region P (red ellipse) that covers at least τ proportion of samples from F_Yt. The shaded region represents the area of the ellipse and visually shows that approximately 90% of the data points fall within this region.

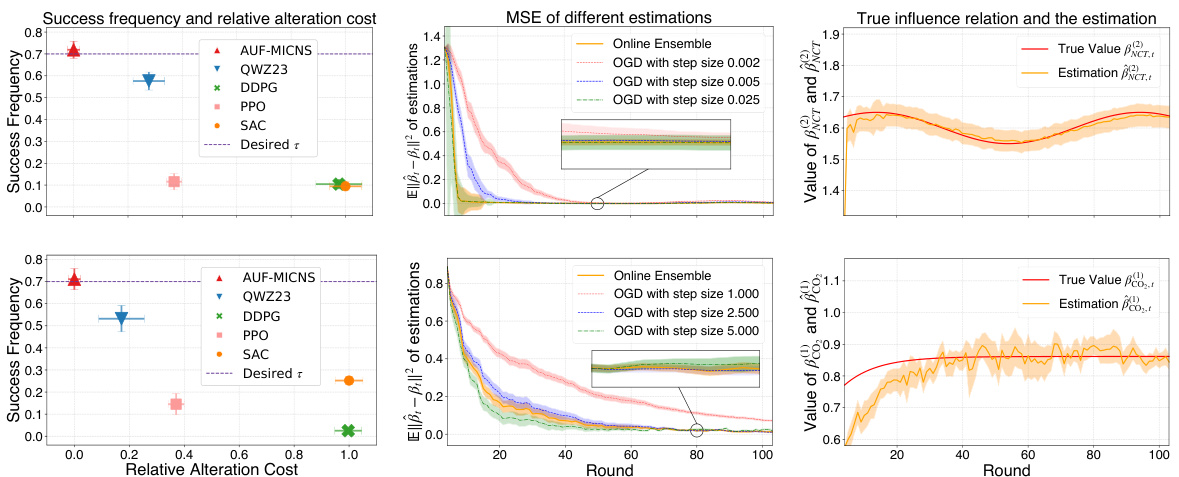
This figure presents the results of two experiments, one using market-managing data and the other using Bermuda data. Each row corresponds to a different dataset. The figure displays four key metrics across multiple rounds of decision-making: success frequency (the percentage of times the desired outcome is achieved), relative alteration cost (a normalized comparison of cost among different methods), the mean-squared error (MSE) of parameter estimations, and a comparison of the true versus estimated influence relations. The bars represent average values, and the bands indicate standard deviations, providing a measure of variability.

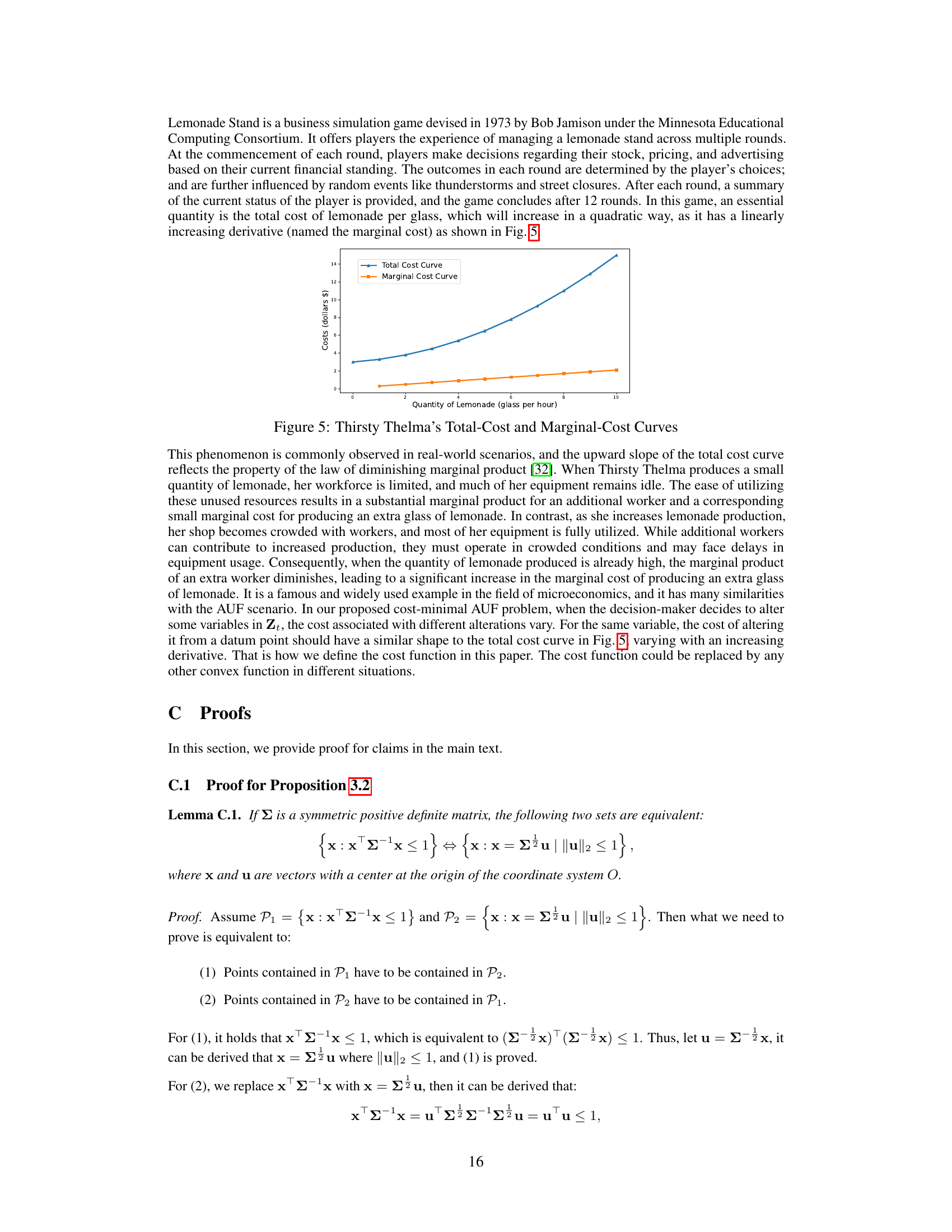
This figure illustrates the concepts of total cost and marginal cost using the example of Thirsty Thelma’s Lemonade Stand. The total cost curve shows the total cost of producing a given quantity of lemonade, while the marginal cost curve shows the additional cost of producing one more glass of lemonade. The upward slope of the total cost curve reflects the law of diminishing marginal product: as production increases, the marginal cost also increases because additional resources are less productive.

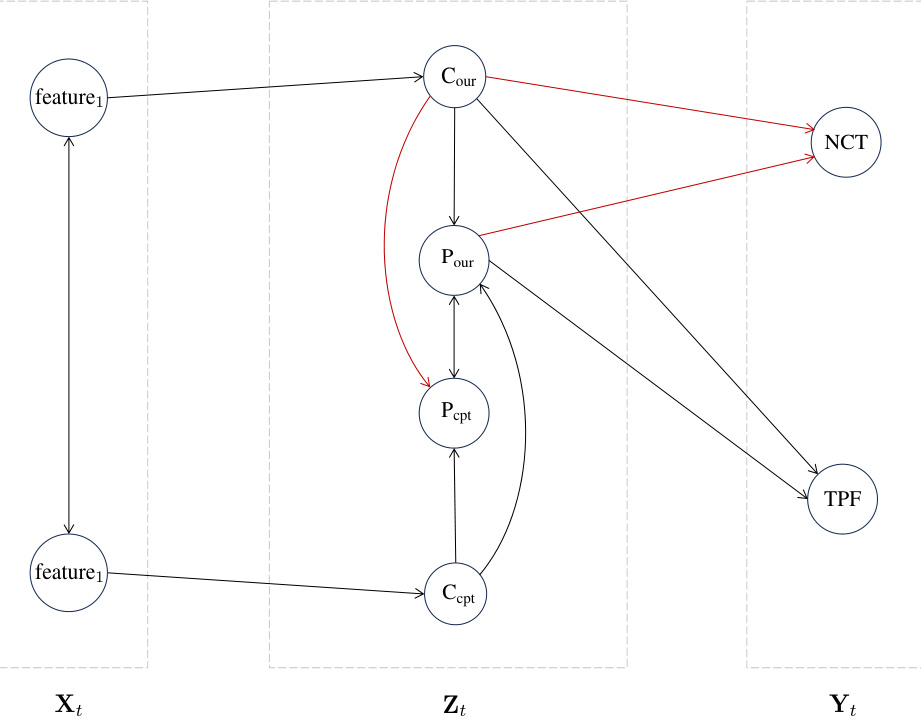
This figure shows the rehearsal graph used for the Market-managing data in the AUF problem. The graph visually represents the influence relations between the variables, showing how different variables (features, intermediate variables, and outcomes) are connected and influence each other. The nodes represent variables, and the directed and bidirectional edges represent the influence relations. The figure helps to visualize the structure of the problem and how the different variables interact to determine the final outcome.

This figure shows the desired regions S for both the Market-managing data and the Bermuda data. The left panel (a) displays the desired region S for the Market-managing data, illustrating the target area for Total Profit (TPF) and Number of Customers (NCT) values. The right panel (b) shows the desired region S for the Bermuda data, indicating the acceptable range for Net Ecosystem Calcification (NEC). The shaded regions represent the target outcome areas, and the points illustrate the distribution of actual data points in the respective spaces.

This figure shows the empirical cumulative distribution function (CDF) of the outcome variable Y for both the Market-managing data and the Bermuda data. The red shaded area represents the desired region S where the outcome is considered desirable, while the blue bars represent the original distribution of Y. The figure visually demonstrates the relatively small portion of the original data that falls within the desired region, highlighting the challenge of the avoiding undesired future (AUF) problem. The x-axis represents the natural value of outcome variable (TPF and NEC for Market and Bermuda respectively), and y-axis is the empirical CDF of Y.

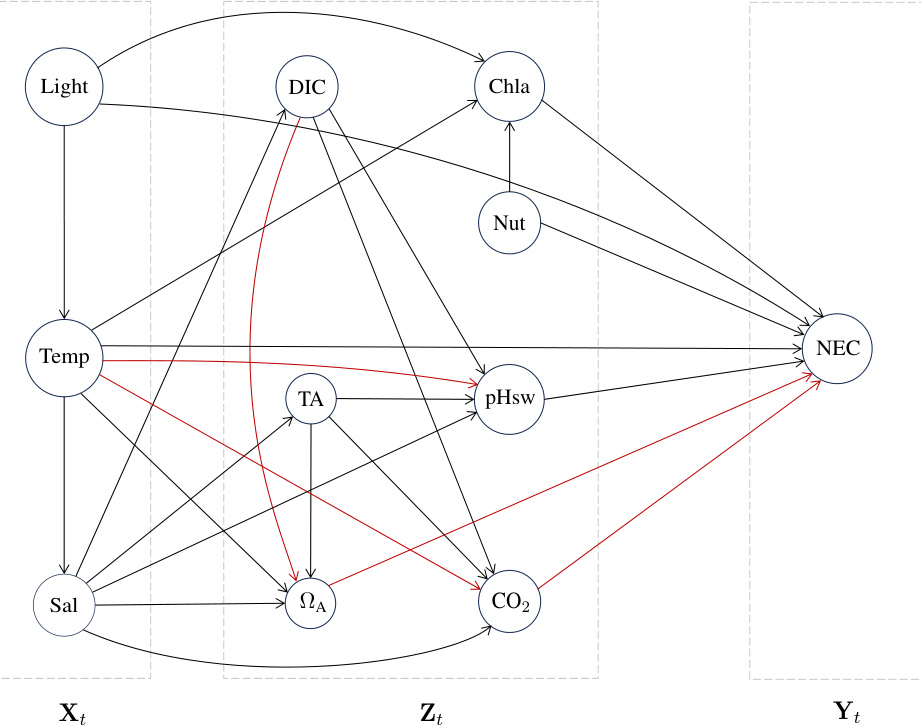
This figure is a rehearsal graph showing the relationships between variables in the Bermuda dataset used in the paper. The nodes represent variables such as light levels, temperature, salinity, dissolved inorganic carbon, total alkalinity, aragonite saturation, chlorophyll-a, nutrient levels, pH, and pCO2. The edges represent the influence relations between these variables, with red edges highlighting dynamic relations that change over time. The variables are grouped into three time segments: X_t (observed variables), Z_t (actionable intermediate variables), and Y_t (the outcome of interest, net ecosystem calcification). This graph structure informs the model used for decision making in the Avoiding Undesired Future (AUF) problem.

More on tables

This table compares the average running time of the AUF-MICNS algorithm with other algorithms (DDPG, PPO, SAC, QWZ23) on two datasets: Market and Bermuda. It highlights the computational efficiency of AUF-MICNS in comparison to existing methods, especially QWZ23, which shares a similar approach for rehearsal-based decision making.

This table shows the average running time of the 20-times experiments for different methods on two datasets (Market and Bermuda). The comparison focuses primarily on AUF-MICNS and QWZ23, as both methods maintain influence relations rather than solely suggesting decisions. The results show that AUF-MICNS is more time-efficient than QWZ23, highlighting a key advantage of the proposed method.

This table compares the average running time (in seconds) of five different algorithms: DDPG, PPO, SAC, QWZ23, and MICNS. The algorithms are evaluated on two datasets: Market and Bermuda. The MICNS algorithm shows significantly faster running times compared to QWZ23, highlighting its efficiency improvement.

This table presents the average running time in seconds for different algorithms (DDPG, PPO, SAC, QWZ23, MICNS) across two datasets (Market and Bermuda). It compares the performance of the proposed AUF-MICNS algorithm against other methods, highlighting its time efficiency, particularly relative to QWZ23.

Full paper

#