TreeVI: Reparameterizable Tree-structured Variational Inference for Instance-level Correlation Capturing

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents TreeVI, a novel approach to variational inference that efficiently handles correlations between data instances. This is a significant advancement as many real-world applications involve such correlations, and it enhances the performance of downstream applications. The introduction of tree structures to model posterior correlation, and the automatic learning of this structure from the data, are key contributions that open doors to more complex and accurate modeling in various fields.

Visual Insights

#

This figure illustrates three different ways to model correlations among latent variables in a variational inference setting. (a) shows a fully connected graph where every pair of latent variables is directly correlated. This approach is highly expressive but computationally expensive. (b) presents TreeVI, which uses a single tree structure to capture correlations. The correlations between non-adjacent nodes are calculated by multiplying the correlations along the path connecting them. This approach reduces computational cost while still capturing high-order correlations. (c) extends this to MTreeVI, a mixture-of-trees model, which further improves the accuracy by allowing more complex correlation structures.

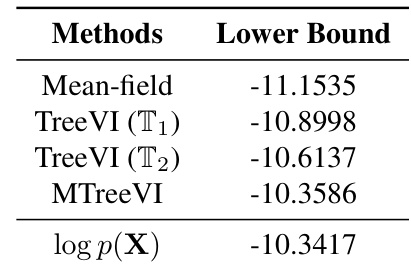
This table presents the estimated lower bounds (ELBO) of a variational autoencoder (VAE) model using different posterior distribution approximations. The methods compared include mean-field, TreeVI with two different tree structures (T1 and T2), and MTreeVI (a mixture of T1 and T2). The results are compared against the ground truth log-likelihood (log p(X)) to evaluate the accuracy of the approximations. Lower ELBO values indicate a less accurate approximation of the true posterior.

In-depth insights

#

TreeVI: Core Idea

#

TreeVI’s core idea centers on addressing the limitations of mean-field variational inference (VI) in capturing instance-level correlations. Mean-field VI’s independence assumption is restrictive, hindering its application to scenarios with inherent dependencies between data points. TreeVI tackles this by employing a tree structure to model the correlation between latent variables in the posterior distribution. This structure allows for efficient, parallel reparameterization, making the approach scalable even with large datasets, unlike many other correlation-aware VI methods. The tree’s topology encodes the correlation structure, and importantly, this tree structure can be learned automatically from data. This learning capability enhances TreeVI’s adaptability and effectiveness across varied applications. The use of a tree, rather than a fully-connected graph, offers a computational advantage, while still enabling the capture of complex relationships through path-based correlations.

Reparameterization

#

Reparameterization in variational inference aims to improve the efficiency and scalability of approximating intractable posterior distributions. By transforming the latent variables using a differentiable function of a simple random variable, reparameterization techniques enable gradient-based optimization methods to be directly applied to the ELBO (Evidence Lower Bound). This avoids the challenges associated with direct sampling from complex distributions. The effectiveness of reparameterization hinges on choosing a suitable transformation that balances computational cost and accuracy. TreeVI leverages reparameterization to efficiently sample from a tree-structured posterior, enabling the capture of instance-level correlations without excessive computational burden. This is a critical advance over traditional mean-field approximations that assume independence, making it particularly beneficial for applications with inherent data dependencies. The matrix-form reparameterization used in TreeVI further enhances its parallelisability and scalability, making it suitable for large datasets.

Multi-Tree Extension

#

The multi-tree extension is a crucial enhancement to the TreeVI model, addressing its limitation of restrictive expressiveness with a single tree. By allowing a mixture of trees, the model can capture more complex and nuanced correlation structures among data instances. This extension significantly increases the model’s ability to accurately approximate the true posterior distribution in scenarios with intricate relationships between latent variables. The use of a weighted mixture further enhances flexibility, allowing the model to adapt to varying degrees of correlation across different subsets of instances. A key challenge is determining the optimal number of trees and their structures, which the paper addresses through a continuous optimization approach. This approach combines stochastic methods with tree structure learning, which is a highly innovative aspect of this model. The overall effect is a more robust and powerful approach to variational inference, suitable for a wider array of complex datasets and downstream applications.

Structure Learning

#

Structure learning, in the context of the provided research paper, focuses on automatically learning the relationships between latent variables, often represented as a tree or a mixture of trees. This is crucial because assuming independence between variables (mean-field approximation) is often unrealistic and limits the model’s ability to capture complex correlations. The method described uses a continuous optimization algorithm to learn the tree structure directly from training data, overcoming the limitation of needing to specify this structure beforehand. This approach addresses the key challenge of balancing expressiveness (capturing rich correlation structure) with scalability, ensuring that the model can be trained effectively on large datasets. A crucial aspect is the efficient reparameterization strategy employed which makes the learning process computationally feasible. The learned structure, represented as a tree or mixture-of-trees, provides a principled way to model high-order correlations among the latent variables, improving the performance of downstream applications. However, the effectiveness might depend on how well the tree structure captures the true underlying relationships within the data, and learning this optimal structure remains a computationally challenging task. Further research could explore techniques to learn more flexible structures, or those that can adapt dynamically during training.

Future Work

#

The authors acknowledge the limitations of relying solely on tree structures to capture complex correlations within the latent variables, suggesting that future work could explore richer, more expressive structures like graphical models or more sophisticated Bayesian networks. They also note the restrictive assumption of acyclicity in the tree structures, proposing to investigate methods to accommodate cyclic correlations. Furthermore, while stochastic learning of tree structures is implemented, exploring alternative methods for learning the optimal tree structure from the training data could improve both efficiency and representational power. Specifically, exploring alternative optimization algorithms beyond gradient-based methods could enhance performance. Finally, extending their approach to handle missing data is another potential avenue for future work, given the prevalence of incomplete datasets in many real-world applications. The authors also note that they only consider pairwise correlations, and higher-order interactions among latent variables could be explored to capture even more intricate dependencies.

More visual insights

#

More on tables

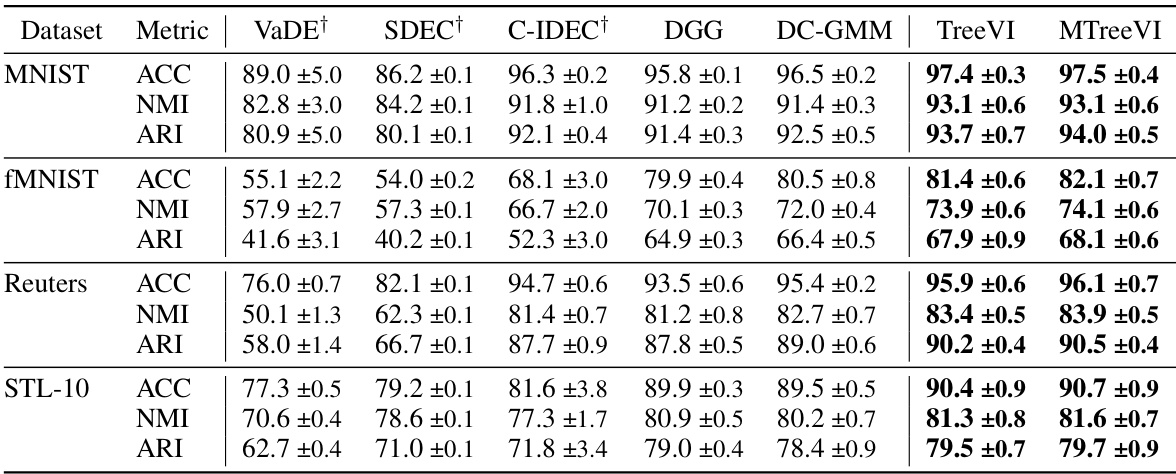
This table presents the clustering performance comparison of TreeVI and MTreeVI against several baseline methods on four datasets: MNIST, Fashion MNIST, Reuters, and STL-10. The metrics used are Accuracy (ACC), Normalized Mutual Information (NMI), and Adjusted Rand Index (ARI). The results are averaged over 10 runs with different random initializations, highlighting the stability and effectiveness of TreeVI and MTreeVI.

This table presents the results of a synthetic user matching experiment. The test metric is Reciprocal Rank (RR), which measures the ranking of the correct match in the list of candidates. The table compares the performance of different methods: VAE, CVAE (independent and correlated versions), TreeVI (single tree), and MTreeVI (multiple trees). Lower values indicate better performance. The results show that the TreeVI and MTreeVI models significantly outperform baselines, demonstrating the effectiveness of capturing instance-level correlations in the posterior distribution.

This table presents the results of a link prediction task on the Epinions dataset. The Normalized Cumulative Reciprocal Rank (NCRR) metric is used to evaluate the performance of various methods. Lower NCRR indicates better prediction performance. The methods compared include VAE, GraphSAGE, CVAE with independent and correlated latent variables, and the proposed TreeVI and MTreeVI methods. The results show that TreeVI and MTreeVI outperform the baseline methods.

This table compares the clustering performance of TreeVI and MTreeVI with several baseline methods on four datasets: MNIST, Fashion MNIST, Reuters, and STL-10. The performance is measured using three metrics: Accuracy (ACC), Normalized Mutual Information (NMI), and Adjusted Rand Index (ARI). The table shows the mean and standard deviation of each metric across 10 runs, each with different random initializations. The results highlight the improvement achieved by TreeVI and MTreeVI over other methods in capturing instance-level correlation.

This table presents the clustering accuracy results on the MNIST dataset using TreeVI with two different tree structure initialization methods (random tree and greedy search) and with/without constrained optimization. It demonstrates the impact of initialization and the effectiveness of the constrained optimization on model performance.

This table shows the hyperparameter settings used for the constrained clustering task. It lists the batch size, number of epochs, learning rate, decay rate, and epochs decay for four different datasets: MNIST, fMNIST, Reuters, and STL-10. These hyperparameters were used to train the constrained clustering models using the proposed TreeVI and MTreeVI methods, as well as baseline methods. The consistent hyperparameter settings across datasets facilitated fair comparison between the proposed method and the baselines.

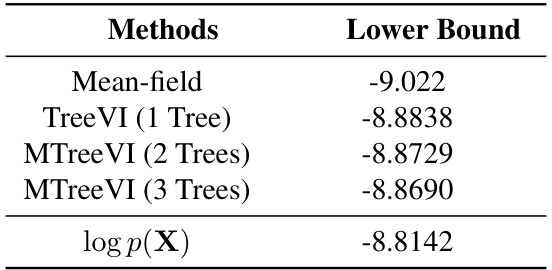
This table presents the ELBO (evidence lower bound) values obtained using various methods for approximating the posterior distribution in a variational autoencoder (VAE) model. The methods compared are mean-field, TreeVI with a single tree, and MTreeVI with multiple trees (2 and 3 trees). The results are compared to the actual log-likelihood (log p(X)) to evaluate the accuracy of the approximation.

This table presents the clustering performance comparison among different methods on four datasets: MNIST, Fashion MNIST, Reuters, and STL-10. The metrics used are accuracy (ACC), normalized mutual information (NMI), and adjusted rand index (ARI). The results are averaged over 10 runs with different random initializations, showcasing the performance of TreeVI and MTreeVI against various baseline constrained clustering methods.

Full paper

#