↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Unsupervised learning (UL)-based solvers offer advantages for combinatorial optimization (CO), but face issues like getting trapped in local optima and requiring artificial rounding. These solvers directly optimize the CO objective using continuous relaxation, but this can lead to suboptimal solutions and undermines the robustness of the results.
This paper introduces Continuous Relaxation Annealing (CRA), a new method to address the issues. CRA introduces a penalty term to control the balance between continuous and discrete solutions during the learning process. The penalty term dynamically shifts from prioritizing continuous solutions (smoothing non-convexity) to enforcing discreteness (eliminating artificial rounding). Experiments show that CRA significantly improves the performance of UL-based solvers, surpassing existing methods in complex CO problems.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses critical limitations of existing unsupervised learning (UL)-based solvers for combinatorial optimization (CO) problems. It introduces Continuous Relaxation Annealing (CRA), a novel method that significantly improves the performance and stability of UL-based solvers. This is highly relevant to current research trends in AI and machine learning, where efficient and robust CO solvers are crucial for various applications. CRA opens up new avenues for further research by addressing two major challenges and suggesting improvements to existing methods.
Visual Insights#
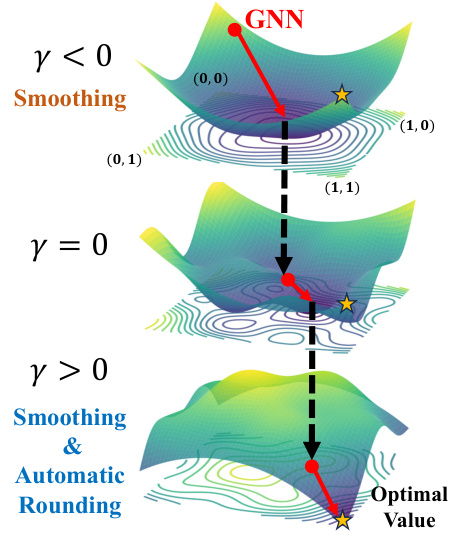
This figure illustrates the annealing process used in the Continuous Relaxation Annealing (CRA) strategy. It shows how the penalty parameter γ dynamically shifts the focus of the optimization process. When γ < 0, the penalty term smooths the non-convex objective function, allowing for broader exploration of the continuous solution space. As γ increases towards 0 and then becomes positive, the penalty term increasingly enforces discreteness, guiding the solution towards the optimal discrete solution. The three panels represent different stages of the annealing process, visually depicted as surfaces with contour lines representing the loss function. The red dots on the surfaces illustrate the solution path during the annealing.

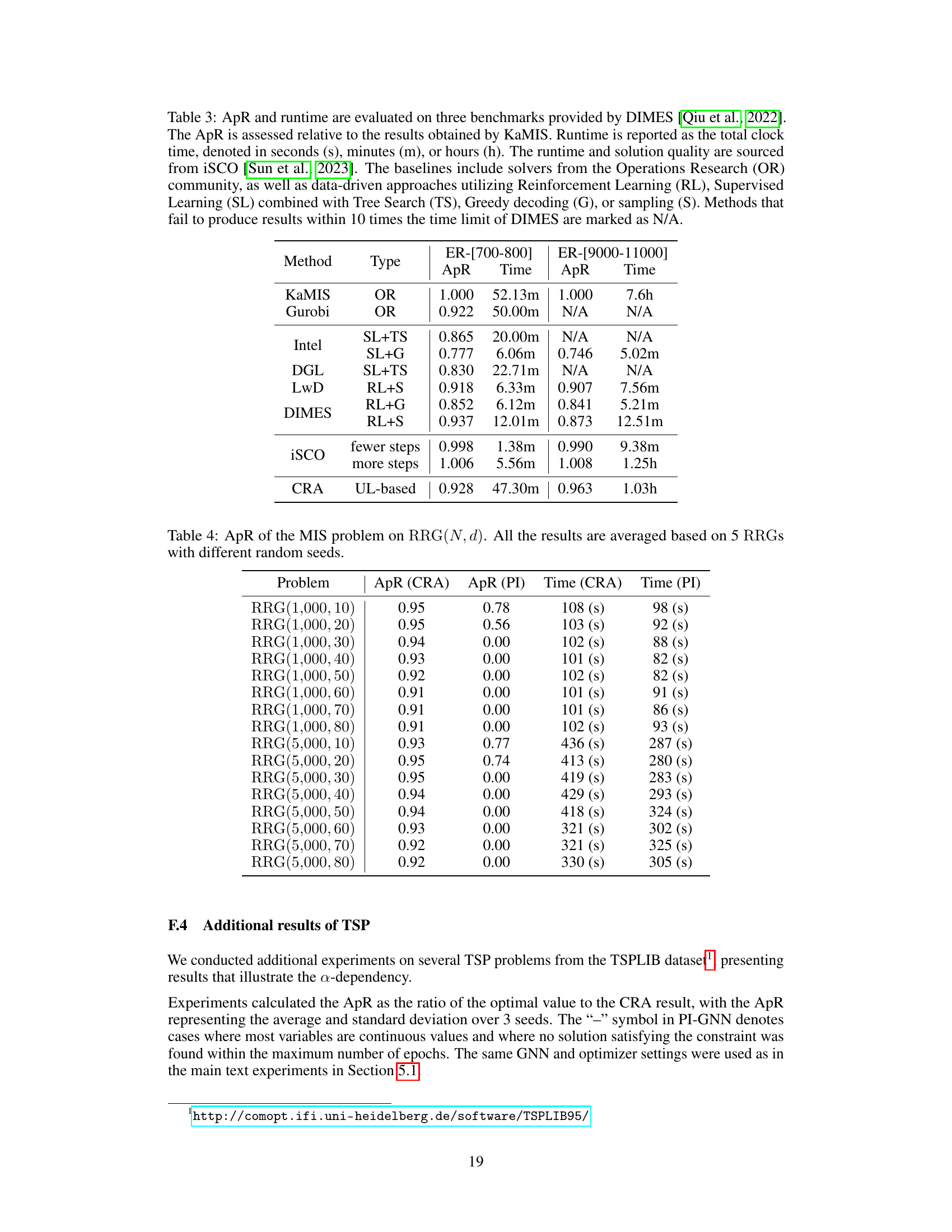
This table presents the approximation ratio (ApR) results for the Maximum Independent Set (MIS) problem on random regular graphs (RRGs) with 10,000 nodes and node degrees of 20 and 100. It compares the performance of several methods: Random Greedy Algorithm (RGA), Degree Greedy Algorithm (DGA), Erdős Goes Neural (EGN), Meta-EGN, Physics-Inspired GNN (PI-GNN) with Graph Convolutional Network (GCN) and GraphSAGE, and the proposed Continuous Relaxation Annealing (CRA) with GCN and GraphSAGE. The ApR is a measure of how close the solution found by each method is to the optimal solution. Lower ApR values indicate better performance.
In-depth insights#
CRA: Annealing CO#
The heading “CRA: Annealing CO” suggests a novel approach to combinatorial optimization (CO) problems. CRA, likely standing for Continuous Relaxation Annealing, appears to be a method that leverages continuous optimization techniques to find solutions for discrete problems. This likely involves starting with a continuous relaxation of the original discrete problem, gradually enforcing discreteness through an annealing process. The annealing process would gradually increase a penalty term (or decrease a smoothing term), which would encourage the solution to move from a continuous space towards a discrete one, potentially avoiding local optima and improving the quality of the final solution. The method’s application to CO problems suggests that it provides a robust solution that avoids the need for ad-hoc rounding procedures often associated with continuous relaxation techniques, ultimately improving the efficiency of CO problem solving.
UL Solvers’ Issues#
Unsupervised learning (UL)-based solvers, while offering advantages for combinatorial optimization (CO) problems, face significant limitations. Local optima trapping is a major issue; UL solvers often get stuck in suboptimal solutions, hindering their ability to find the true optimum. This is particularly problematic for complex, large-scale problems. Additionally, the use of artificial rounding to convert soft solutions from the continuous relaxation back to the discrete space introduces ambiguity and undermines the reliability of the results. The requirement for such rounding highlights the inherent limitations of representing discrete problems within a continuous framework. Generalization issues are also present, with models often failing to generalize effectively to unseen instances. This necessitates either large training datasets or the adaptation of the learning algorithm to individual problem instances which can be computationally expensive.
GNN Architecture#
The effectiveness of Graph Neural Networks (GNNs) in combinatorial optimization hinges significantly on their architecture. A well-designed GNN architecture must efficiently aggregate and process information from the graph’s structure and node features. This necessitates careful consideration of layer depth, the choice of aggregation functions (e.g., mean, sum, max pooling), and the type of message-passing mechanisms employed. Overly deep architectures can lead to vanishing gradients and hinder learning, whereas shallow architectures may lack the capacity to capture complex relationships within the graph. The selection of aggregation and combination functions directly influences the expressiveness and efficiency of the model. Furthermore, the choice of activation functions, normalization techniques, and any incorporated skip connections or attention mechanisms play a vital role in the GNN’s performance and should be tailored to the specific characteristics of the optimization problem. Ultimately, effective GNN architectures for combinatorial optimization require a nuanced balance between model complexity and computational cost, requiring thorough experimentation and careful design choices.
Empirical Results#
An effective ‘Empirical Results’ section would meticulously detail experimental setups, including datasets used, evaluation metrics, and baseline methods. It would then present the results clearly and concisely, using tables and figures where appropriate, comparing the proposed method’s performance against established baselines. Key findings regarding the method’s effectiveness in handling different problem scales, data characteristics, and hyperparameter settings should be highlighted. Statistical significance of results should be rigorously addressed, with proper error bars and significance tests. The discussion of the results should not just state findings but also analyze them in depth, providing plausible explanations for successes and failures, and connecting them back to the paper’s theoretical contributions. A strong conclusion would summarize the main findings, acknowledging limitations and suggesting directions for future work, and emphasizing the practical implications and impact of the work.
Future of UL-CO#
The future of unsupervised learning for combinatorial optimization (UL-CO) is promising, driven by the need to solve large-scale, complex problems where traditional methods fail. Continuous Relaxation Annealing (CRA), a novel rounding-free learning method, represents a significant advance, addressing the limitations of existing UL-based solvers. CRA enhances performance by dynamically shifting the penalty term’s focus, smoothing non-convexity initially and then enforcing discreteness to eliminate artificial rounding. This leads to improved solution quality and faster training. Future research should explore more sophisticated penalty functions and annealing schedules to further refine the CRA approach. Moreover, the integration of other techniques, like advanced GNN architectures and meta-learning strategies, could enhance scalability and generalization. Addressing the challenges of escaping local optima and handling various problem structures remains critical. Ultimately, the continued development of UL-CO methods holds the potential to revolutionize diverse fields dependent on efficient combinatorial problem-solving.
More visual insights#
More on figures

This figure shows the computational runtime of the CRA-PI-GNN solver using two different Graph Neural Network (GNN) architectures, GraphSage and Conv, on 100-regular random graphs (RRGs) with varying numbers of nodes (N). The y-axis represents the solution runtime in seconds, and the x-axis represents the number of nodes (N). Error bars indicate the standard deviations of the results, showing the variability in runtime across different runs. The figure aims to demonstrate the scalability of the CRA-PI-GNN solver as the problem size increases. The near-linear scaling of the runtime suggests good scalability.

This figure shows the training curves of the cost function f(x;C) for the Maximum Independent Set (MIS) problem on random regular graphs (RRGs) with 10,000 nodes. Different lines represent different degree values (d = 3, 5, 20, 100), and the curves for the PI-GNN (original method) and CRA-PI-GNN (with two different initial values of γ) are shown. The plots illustrate how the cost function changes over training epochs for the four different scenarios. This highlights the performance differences between PI-GNN and CRA-PI-GNN, and the effect of the annealing parameter γ on the training process, particularly concerning the avoidance of local optima.

This figure shows the approximation ratio (ApR) achieved by PI-GNN and CRA-PI-GNN on 27 diverse bipartite matching (DBM) problem instances. The results demonstrate that CRA-PI-GNN consistently outperforms PI-GNN across all instances, indicating the effectiveness of the CRA approach in enhancing solution quality for practical, non-graph based combinatorial optimization problems.
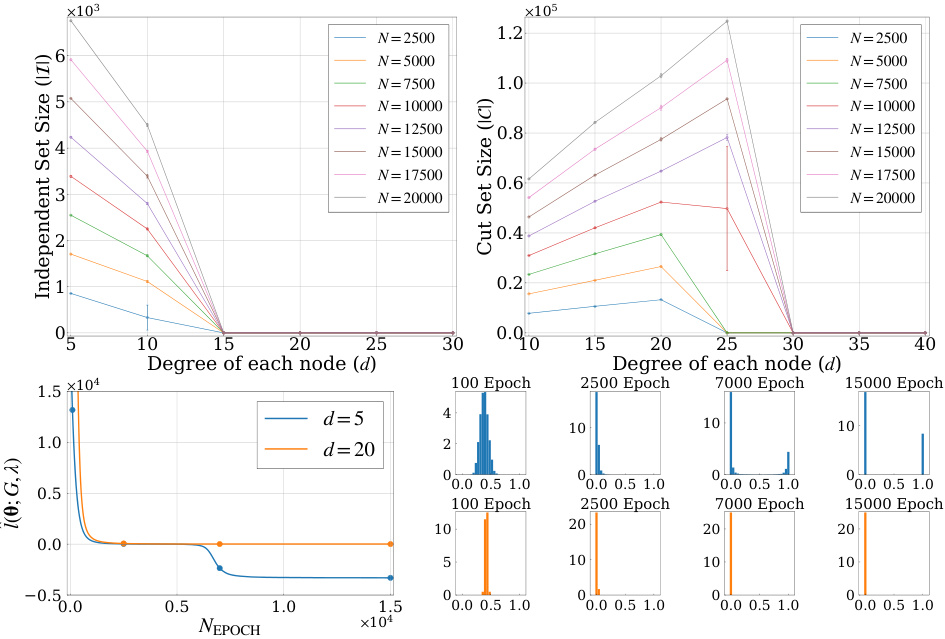
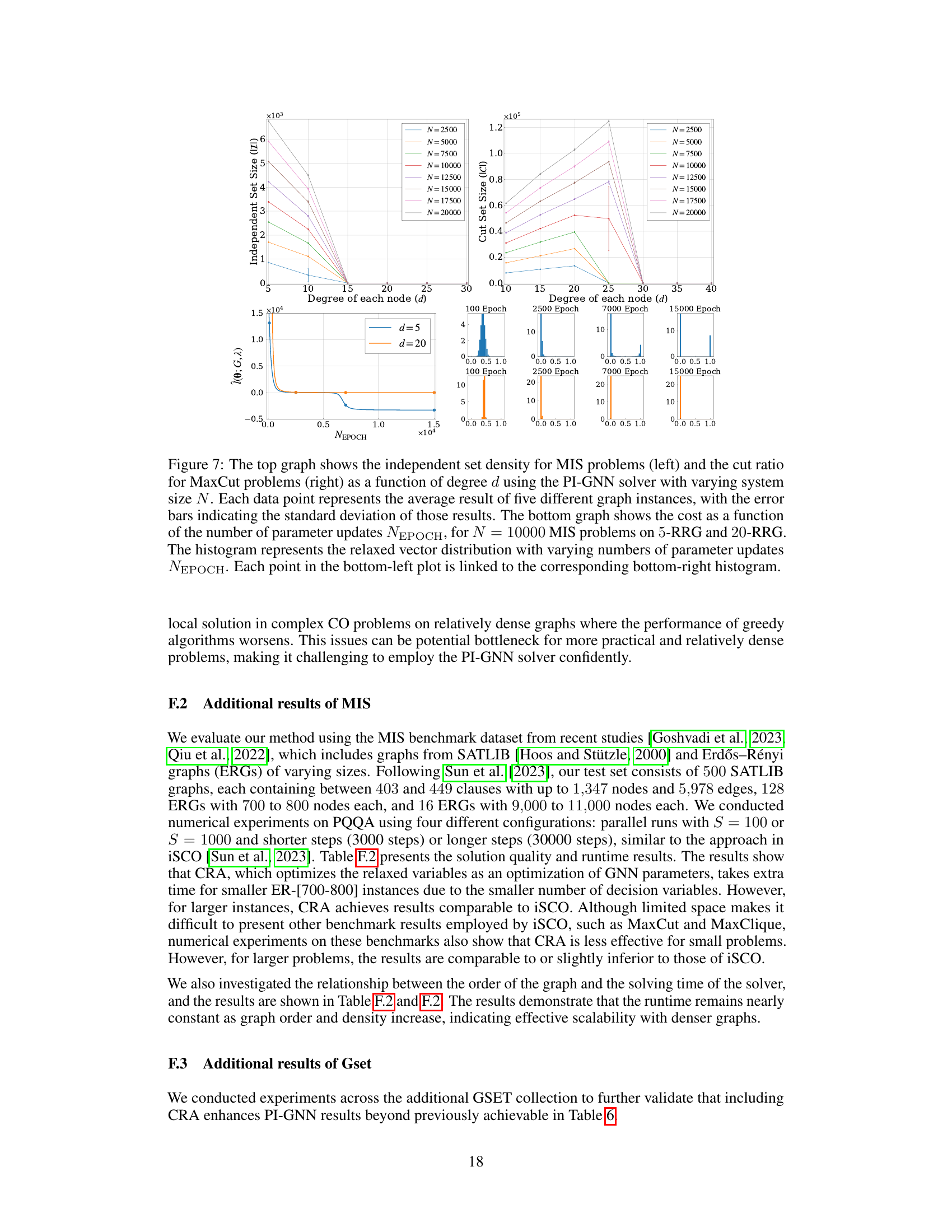
This figure compares the performance of the PI-GNN solver for the Maximum Independent Set (MIS) and MaxCut problems on random regular graphs (RRGs) with varying degrees (d) and number of nodes (N). The top plots show the independent set density (MIS) and cut ratio (MaxCut) as functions of d, illustrating how the PI-GNN solver struggles to find optimal solutions in denser graphs (higher d). The bottom plots show the dynamics of the cost function for MIS problems on 5-RRG and 20-RRG, highlighting how the solver gets trapped in local optima, especially for denser graphs.

This figure displays the impact of the curve rate (α) parameter on the performance of the CRA method for two different problems: Maximum Independent Set (MIS) and MaxCut. The left panel shows the independent set density for MIS problems with degrees d=5 and d=20, indicating that higher curve rates lead to lower density but varying effects across different degrees. The right panel shows the cut ratio for MaxCut problems with degrees d=5 and d=35. Here, the cut ratio appears to be less sensitive to changes in the curve rate compared to MIS.
More on tables
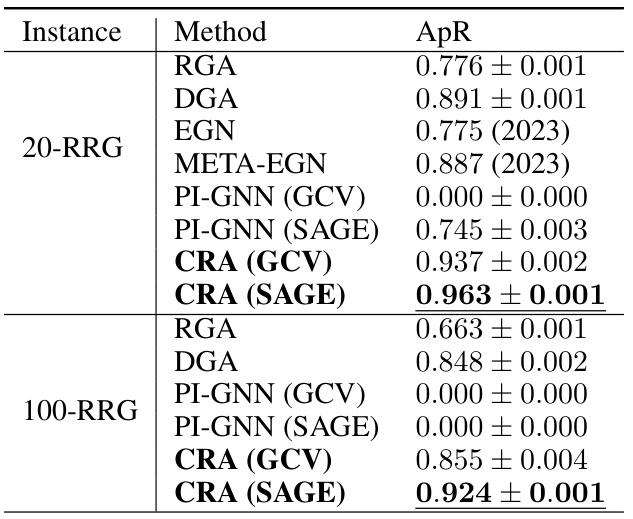
This table presents the approximation ratio (ApR) achieved by different methods on Maximum Independent Set (MIS) problems using random regular graphs (RRGs) with 10,000 nodes and degrees of 20 and 100. The methods compared include traditional greedy approaches (RGA, DGA), other unsupervised learning-based solvers (EGN, META-EGN), the physics-inspired graph neural network (PI-GNN) solver, and the proposed Continuous Relaxation Annealing (CRA) method combined with PI-GNN (CRA-PI-GNN). The results show that the CRA-PI-GNN significantly outperforms other methods, demonstrating its effectiveness in solving MIS problems.
This table compares the approximation ratio (ApR) achieved by different methods for solving the Maximum Independent Set (MIS) problem on random regular graphs (RRGs) with 10,000 nodes and degrees of 20 and 100. The methods include a random greedy algorithm (RGA), a degree-based greedy algorithm (DGA), the Erdős Goes Neural (EGN) solver, a Meta-EGN solver, the Physics-inspired GNN (PI-GNN) solver (using both GCN and GraphSage architectures), and the proposed Continuous Relaxation Annealing (CRA) approach with the PI-GNN solver (also using GCN and GraphSage). The ApR is a measure of the solution quality relative to the optimal solution, with 1.000 representing a perfect solution. The results show that CRA significantly improves the ApR compared to other methods.
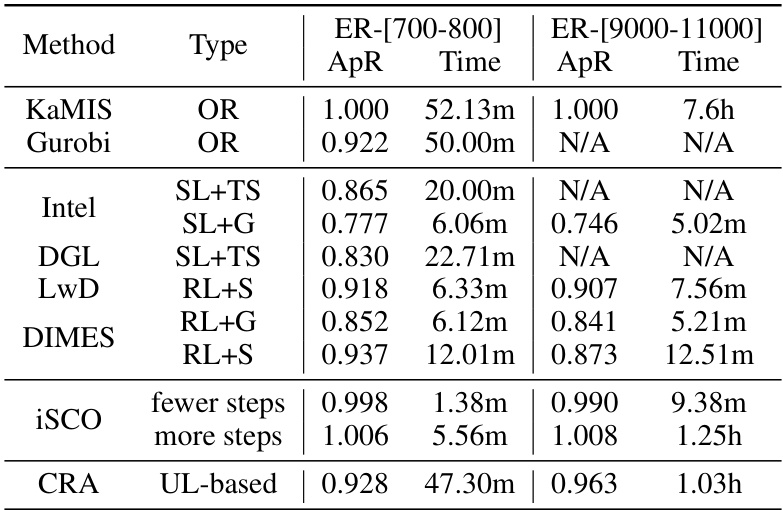
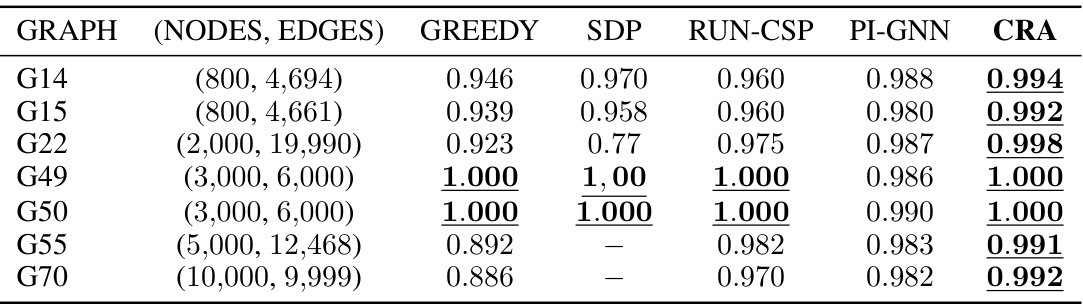
This table compares the performance of various methods for solving combinatorial optimization problems on three benchmark datasets. The approximation ratio (ApR), representing the solution quality relative to the optimal solution, and runtime are reported for each method. The methods include traditional optimization solvers, as well as machine learning based approaches such as Reinforcement Learning, Supervised Learning, and unsupervised learning approaches.
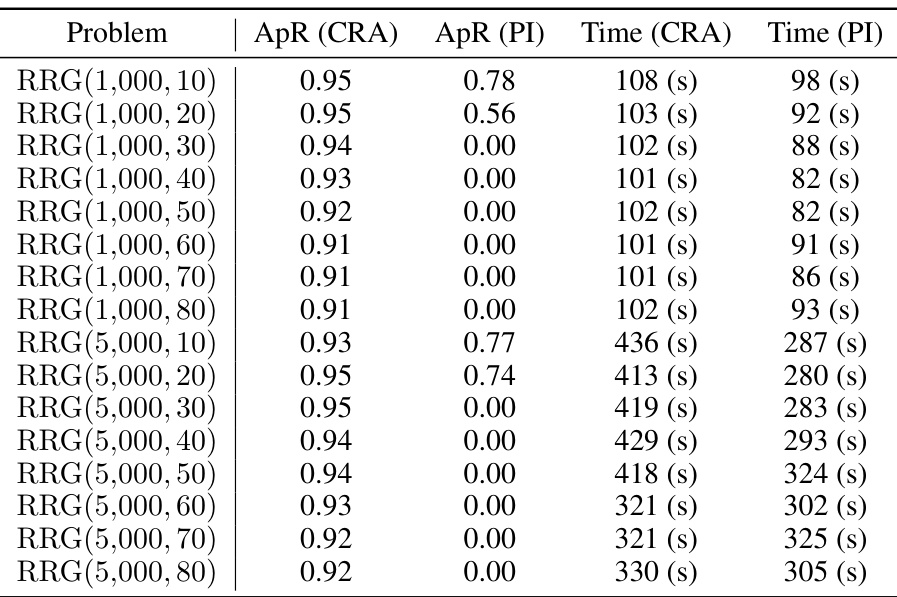
This table presents the approximation ratio (ApR) for the Maximum Independent Set (MIS) problem on random regular graphs (RRGs) with varying numbers of nodes (N) and degrees (d). The results are obtained using both the proposed CRA-PI-GNN method and the original PI-GNN method. For each configuration of N and d, five different RRGs were generated and the ApR was calculated for each. The ApR values shown represent the average across these five runs. The table shows that the CRA-PI-GNN method consistently achieves higher ApR values than the PI-GNN method, indicating its improved performance.

This table presents the approximation ratio (ApR) achieved by different methods for solving the Maximum Independent Set (MIS) problem on random regular graphs (RRGs) with 10,000 nodes and node degrees of 20 and 100. The methods compared include the random greedy algorithm (RGA), the degree-based greedy algorithm (DGA), the Erdős Goes Neural (EGN) solver, the Meta-EGN solver, the Physics-Inspired Graph Neural Network (PI-GNN) solver (with both Graph Convolutional Network (GCN) and GraphSAGE architectures), and the proposed Continuous Relaxation Annealing (CRA) solver (also with GCN and GraphSAGE). The ApR is a measure of solution quality, with 1.00 representing the optimal solution. The results show that the CRA method significantly outperforms other methods, demonstrating its effectiveness in solving this challenging combinatorial optimization problem.

This table presents the approximation ratio (ApR) achieved by different methods for solving the Maximum Independent Set (MIS) problem on random regular graphs (RRGs) with 10,000 nodes and node degrees of 20 and 100. The methods compared include Random Greedy Algorithm (RGA), Degree-based Greedy Algorithm (DGA), Erdős Goes Neural (EGN) solver, Meta-EGN solver, Physics-inspired GNN (PI-GNN) solver (with both Graph Convolutional Network and GraphSage architectures), and the proposed Continuous Relaxation Annealing (CRA) approach with PI-GNN (CRA). The ApR is calculated relative to the theoretical optimal solution.

This table compares the approximation ratio (ApR) performance of the CRA-PI-GNN solver across different values of hyperparameter ‘p’ for several instances from the TSPLIB dataset. It shows the ApR results for p=2, 4, 6, and 8, along with the ApR obtained by the original PI-GNN solver and the optimal solution for each problem instance. This helps to understand the impact of hyperparameter ‘p’ on the accuracy of the solver.
Full paper#