Discrete-state Continuous-time Diffusion for Graph Generation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel approach to graph generation, addressing limitations of existing methods. DISCO’s flexible sampling process and strong theoretical foundation provide a significant advancement, offering improved efficiency and accuracy. This opens new avenues for research in various applications like drug discovery and circuit design.

Visual Insights

#

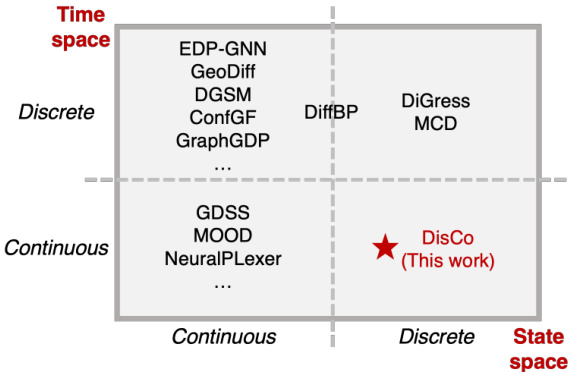
This figure shows a taxonomy of graph diffusion models, categorized by the space of states (discrete or continuous) and time steps (discrete or continuous). It highlights the position of the proposed DISCO model (Discrete-state Continuous-time) within the existing landscape of diffusion models used for graph generation. The figure shows that DISCO occupies a unique position, as previous works have not yet explored this specific combination of discrete states and continuous time.

This table presents the quantitative results of the proposed DISCO model and several other state-of-the-art graph generation models on two benchmark datasets: SBM and Planar. The metrics used to evaluate model performance are Degree (Deg.), Clustering (Clus.), Orbit counts (Orb.), Uniqueness, Novelty, and Validity. Lower values for Deg., Clus., and Orb. are better, while higher values for Uniqueness, Novelty, and Validity are preferred. The results show the mean and standard deviation of each metric across multiple runs.

In-depth insights

#

CTMC-based Diffusion

#

CTMC-based diffusion models offer a powerful framework for generative modeling by leveraging the properties of continuous-time Markov chains (CTMCs). The continuous-time aspect allows for flexible sampling, unlike discrete-time methods, enabling a trade-off between sample quality and computational efficiency. By defining a CTMC over a state space, the model can naturally incorporate the dynamics of the system, leading to a more realistic and nuanced generation process. However, the complexity of working with continuous-time systems needs to be considered. Approximations, such as t-leaping, are often employed to manage computational cost. The choice of the rate matrix, defining the transition probabilities in the CTMC, is crucial, as it directly influences the generated samples’ characteristics and fidelity. Effective training strategies, including careful design of the forward and reverse diffusion processes, are essential for successful model learning. Careful analysis of the model’s properties, such as permutation invariance/equivariance, is important to ensure its suitability for specific data types like graphs, where node ordering is irrelevant to the data structure’s meaning. Future research might explore more efficient numerical methods for continuous-time simulations and more sophisticated ways to select the rate matrix for optimal generative performance.

DISCO Model

#

The DISCO model, a novel approach to graph generation, stands out for its discrete-state continuous-time framework. This unique design elegantly preserves the inherent discrete nature of graph data while offering the flexibility of continuous-time diffusion models. Unlike discrete-time counterparts, DISCO’s continuous-time setting allows for flexible sampling, enabling a trade-off between sample quality and computational efficiency. The model’s training objective boasts a strong theoretical foundation, directly linking it to generation quality and showcasing ideal equivariant/invariant properties under node permutations. By using either a Graph Transformer or a simpler Message Passing Neural Network as its backbone, DISCO demonstrates competitive performance on various benchmarks while maintaining its unique sampling advantages. This makes DISCO a significant advancement in graph generative models, offering both theoretical rigor and practical efficiency.

Sampling Flexibility

#

Sampling flexibility in diffusion models is a crucial advantage, offering control over the trade-off between sample quality and computational cost. Continuous-time approaches provide this flexibility by decoupling the number of sampling steps from the model’s training, allowing for on-demand adjustment of sampling complexity. In contrast, discrete-time methods typically fix the number of steps during training, limiting this control. The ability to adjust sampling granularity is particularly important for graph generation, where the complexity scales significantly with graph size. A model with high sampling flexibility enables efficient generation of small graphs with high fidelity while allowing for more refined sampling (at increased computational expense) for larger, more intricate structures. This adaptability makes continuous-time discrete-state models, like the one proposed in the paper, especially well-suited for graph generation tasks where the discrete nature of the data must be preserved.

Equivariance/Invariance

#

The concept of equivariance/invariance is crucial for understanding the behavior of the proposed model, DISCO, under data transformations. Equivariance, in this context, means that if the nodes of a graph are permuted, the model’s output (predictions, etc.) will also undergo the same permutation. This is essential because graph data is inherently invariant to node ordering. Invariance, on the other hand, signifies that some aspects of the model’s internal workings or outputs remain unchanged despite node permutations. Theorems 3.8 and 3.9 rigorously prove that DISCO’s training objective and sampling distribution exhibit desirable permutation invariance properties. This is critical since it ensures the model’s outputs are not arbitrary artifacts of a specific node ordering, but rather reflect intrinsic graph properties. The backbone model (either Graph Transformer or MPNN) plays a critical role in achieving this equivariance/invariance, highlighting the importance of using architectures that respect the underlying symmetry of the graph data. Careful design and analysis of the equivariance/invariance properties are significant factors contributing to DISCO’s robustness and generalization capabilities.

Future Directions

#

Future research could explore extending the model to handle graphs with non-categorical node and edge features, moving beyond the current categorical limitation. This would significantly broaden the applicability of the model to more complex real-world scenarios. Addressing the quadratic complexity associated with the current complete graph representation is crucial. This could involve exploring more efficient graph representations or developing alternative methods to capture long-range dependencies without relying on a fully connected structure. Investigating the performance and scalability of the model with larger graphs is also vital. Further theoretical analysis could focus on the convergence properties of the model and the tightness of the approximation bounds presented in the paper. Finally, applying the model to various real-world tasks beyond the benchmarks presented, such as drug discovery and circuit design, could provide further validation of its efficacy and highlight potential areas of improvement. This could also involve careful analysis of the model’s robustness to different types of noise and uncertainty in real-world graph data.

More visual insights

#

More on figures

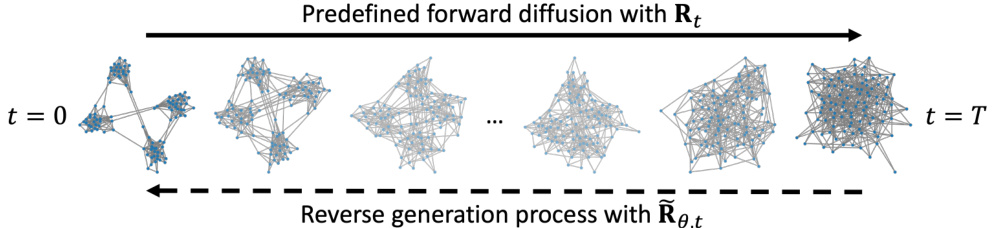
This figure illustrates the forward and reverse diffusion processes in the DISCO model. The forward diffusion process starts at time t=0 with a graph, and it is gradually corrupted (edges and nodes become grayer) until it reaches a noisy state at time t=T. The reverse process then takes this noisy graph at time t=T and iteratively refines it (edges and nodes become less gray) to reconstruct a clean graph that resembles the original graph.

This figure presents a taxonomy of graph diffusion models, categorizing them based on whether they use discrete or continuous state and time spaces. It visually represents the different approaches to graph generation using diffusion models and shows the position of the proposed model, DISCO, within this landscape. DISCO is highlighted as a discrete-state, continuous-time model, differentiating it from other existing models.

This figure presents a taxonomy of graph diffusion models, categorizing them based on the space of states (discrete or continuous) and time steps (discrete or continuous). It visually represents the different models discussed in the paper and highlights the proposed model, DISCO, as a discrete-state continuous-time diffusion model.

This figure presents a taxonomy of graph diffusion models, categorized by the space of states (discrete or continuous) and time (discrete or continuous). It visually represents the different approaches used in graph generation, highlighting the position of the proposed DISCO model within the landscape of existing methods.

More on tables

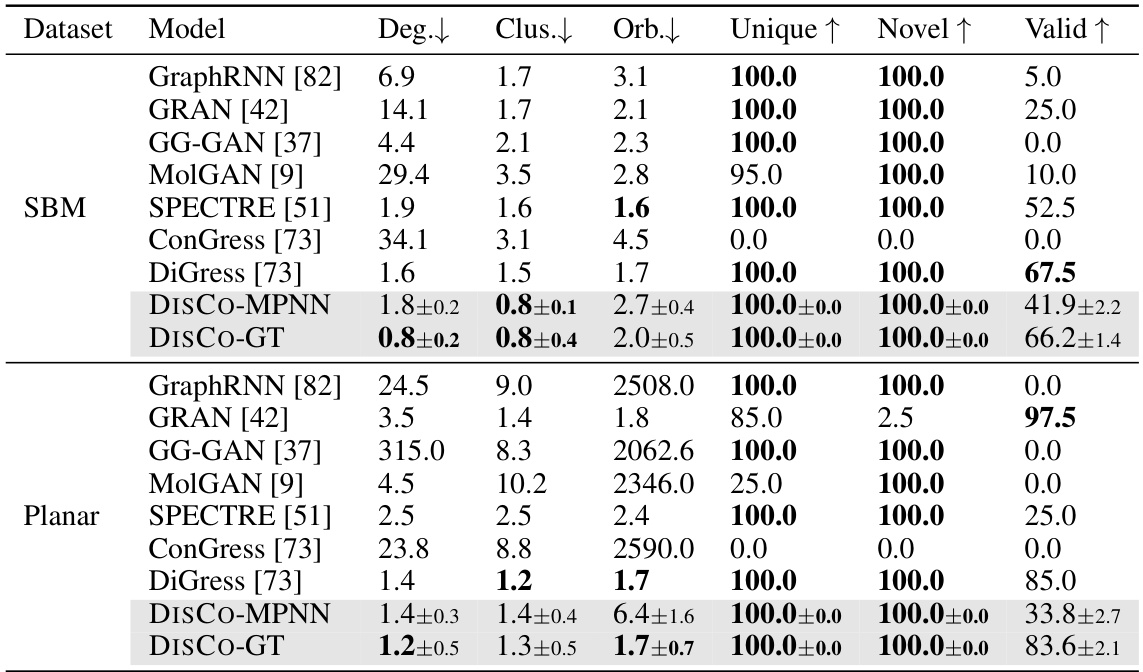
This table presents the performance comparison of various graph generation models on two benchmark datasets: SBM and Planar. For each model and dataset, the table shows the mean and standard deviation of several metrics: Deg. (degree distribution relative squared MMD), Clus. (clustering coefficient distribution relative squared MMD), Orb. (orbit counts distribution relative squared MMD), Unique (percentage of unique graphs generated), Novel (percentage of novel graphs generated), and Valid (percentage of valid graphs generated). Lower values for Deg., Clus., and Orb. are better, while higher values for Unique, Novel, and Valid are preferred. The results show that DISCO-MPNN and DISCO-GT generally outperform the other models, especially in terms of generating unique and valid graphs.

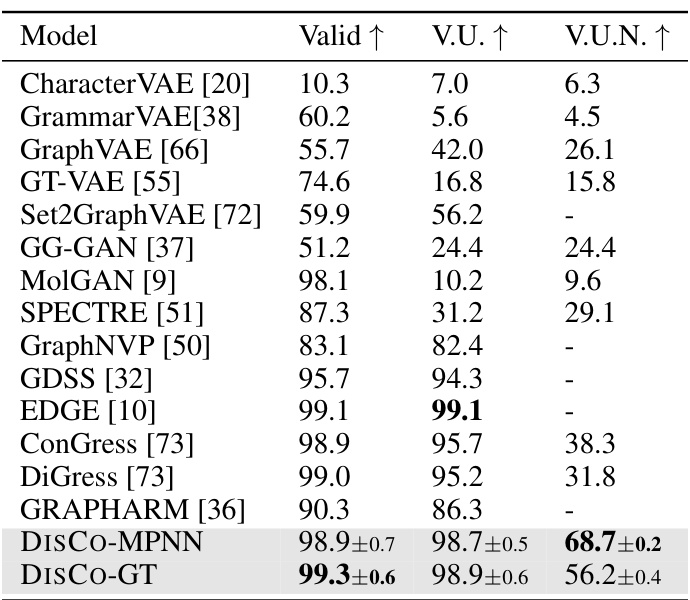
This table presents the performance of various graph generative models on the QM9 dataset. The models are evaluated based on three key metrics: Validity (V.), Uniqueness (U.), and Novelty (N.). Validity refers to the percentage of generated molecules that are chemically valid. Uniqueness indicates the proportion of unique molecules generated. Novelty represents the fraction of generated molecules that are novel compared to the training data. The table shows the mean and standard deviation of these metrics for each model.

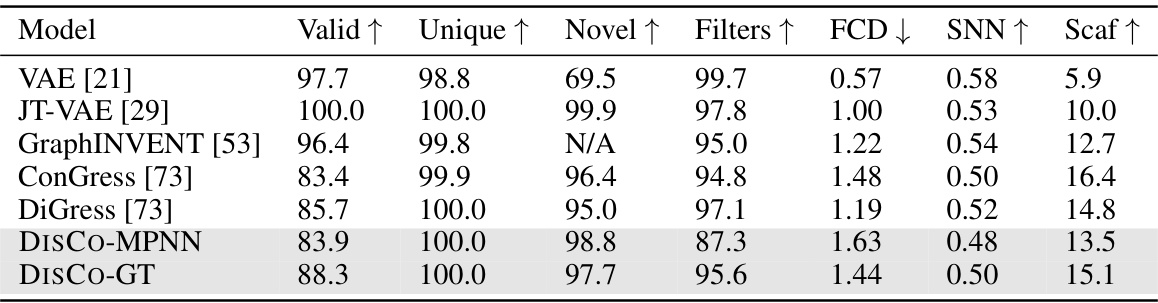
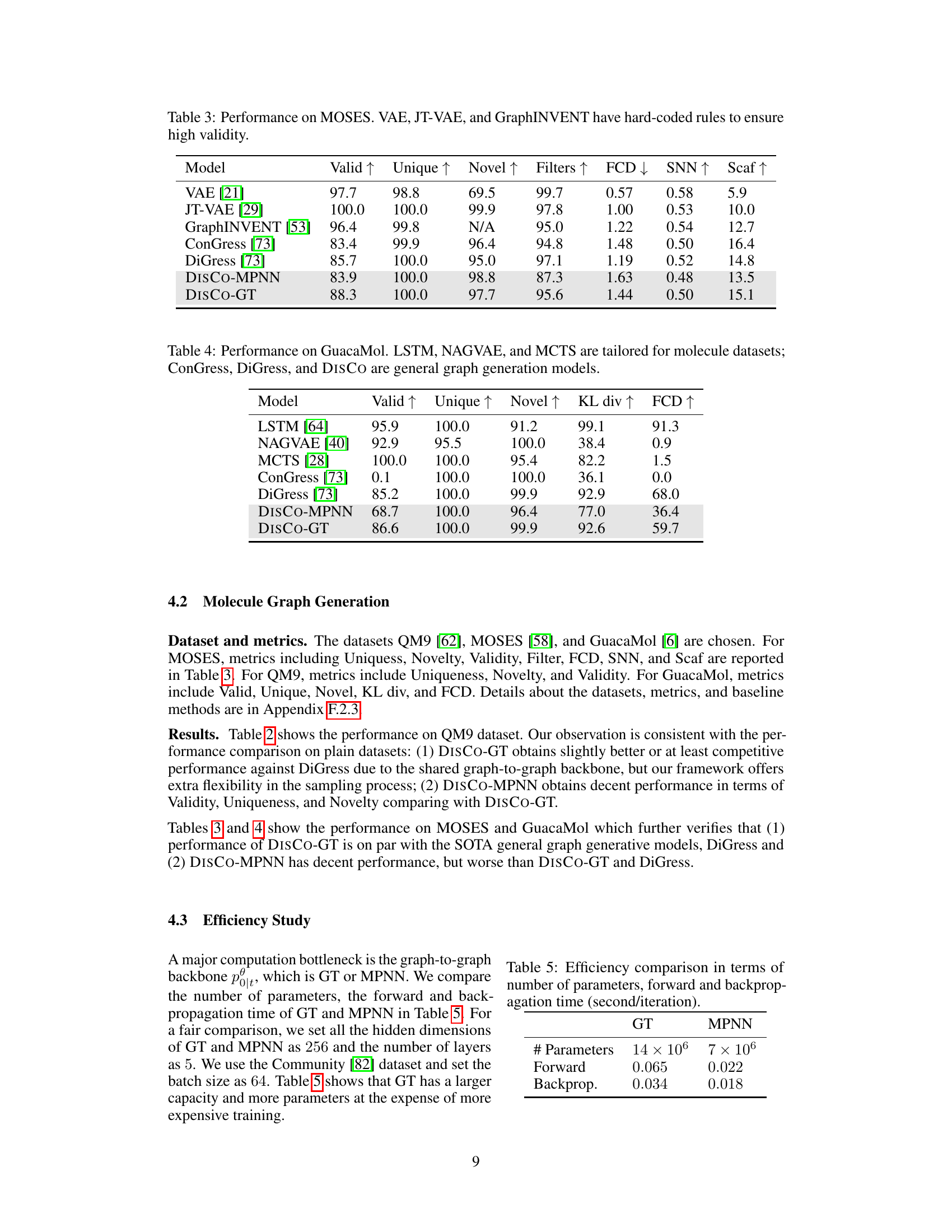
This table presents the performance comparison of different molecular graph generative models on the MOSES dataset. The metrics used to evaluate the models include: Validity (percentage of generated molecules with valid SMILES strings), Uniqueness (percentage of unique molecules), Novelty (percentage of molecules not present in the training set), Filters (number of filters used in the model), FCD (Fréchet ChemNet Distance), SNN (similarity to nearest neighbor), and Scaf (scaffold similarity). Note that VAE, JT-VAE, and GraphINVENT employ hard-coded rules to guarantee high validity, indicating that their performance in this metric might not be directly comparable to the other models that do not use such rules.

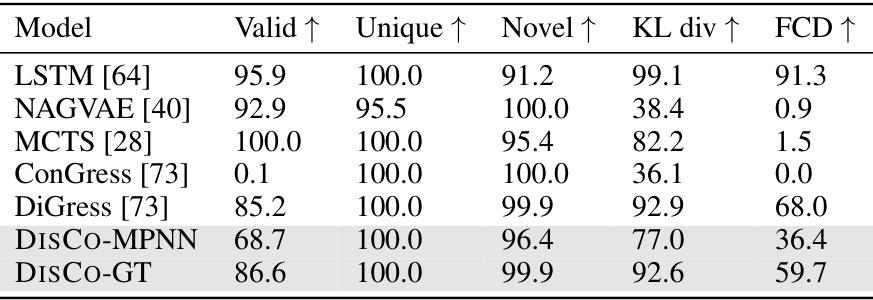
This table presents the performance of various graph generation models on the GuacaMol dataset. It compares the performance of models specifically designed for molecular datasets (LSTM, NAGVAE, MCTS) against general-purpose graph generation models (ConGress, DiGress, DISCO). The metrics used to evaluate the models are Validity, Uniqueness, Novelty, KL Divergence, and FCD.

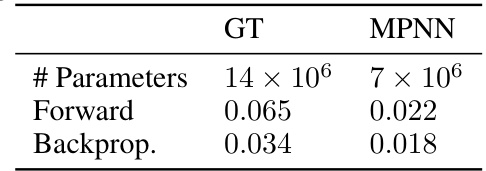
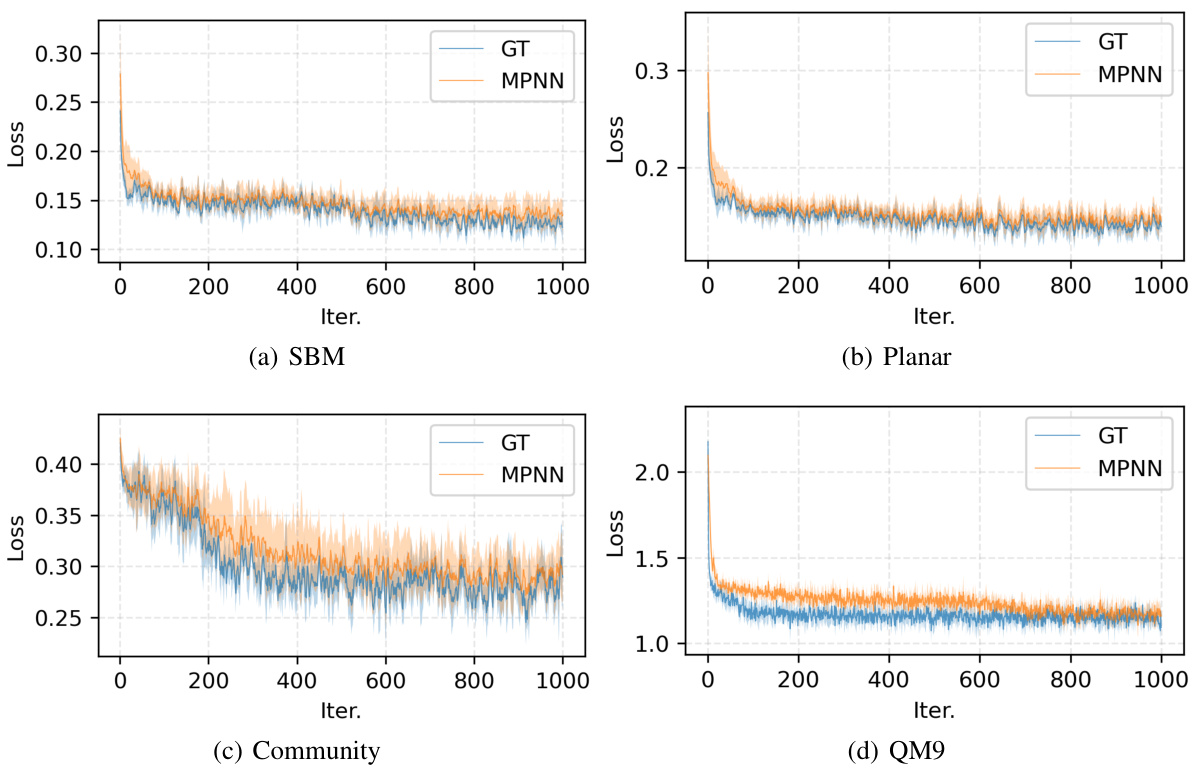
This table compares the computational efficiency of the Graph Transformer (GT) and Message Passing Neural Network (MPNN) architectures used in the DISCO model. It shows the number of parameters, forward pass time, and backpropagation time for each architecture. This is important for understanding the trade-offs between model complexity and computational cost.

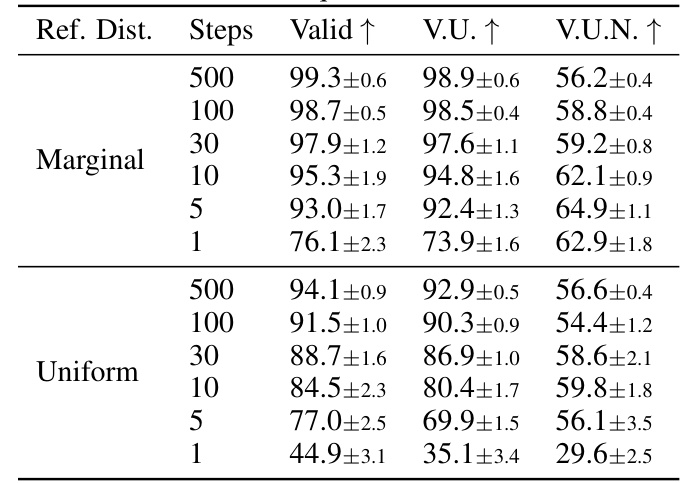
This ablation study investigates the impact of different reference distributions (marginal vs. uniform) and varying numbers of sampling steps (1 to 500) on the performance of the DISCO-GT model. The results are presented in terms of Validity, Uniqueness, and Novelty metrics, offering insights into the model’s robustness and sensitivity to these hyperparameters.

This table presents the statistics of six graph datasets used in the paper’s experiments. For each dataset, it lists the number of graphs, the split into training, validation, and testing sets, the number of edge types (a), the number of node types (b), the average number of edges (Avg. |E|), the maximum number of edges (Max |E|), the average number of nodes (Avg. |F|), and the maximum number of nodes (Max |F|). The datasets include both plain graph datasets (SBM, Planar, Community) and molecular graph datasets (QM9, MOSES, GuacaMol). This information is crucial for understanding the scale and characteristics of the data used in evaluating the proposed model.

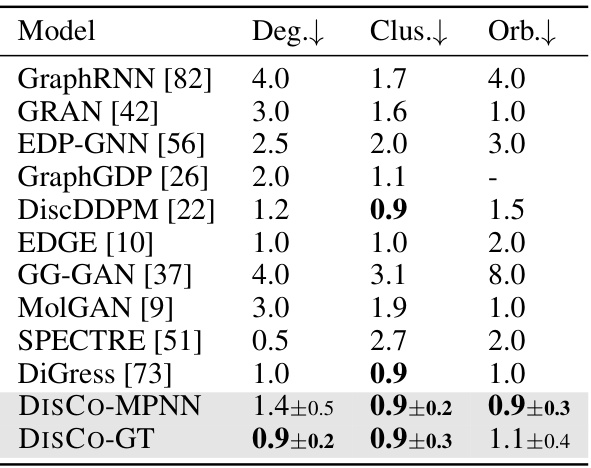
This table presents the performance of various graph generation models on the Community dataset. The models are evaluated using three metrics: Deg. (degree distribution), Clus. (clustering coefficient distribution), and Orb. (orbit counts distribution). Lower values indicate better performance for these metrics. The table includes results for several state-of-the-art models (GraphRNN, GRAN, EDP-GNN, etc.) and the proposed DISCO model with both MPNN and GT backbones. The table allows for comparison of the proposed method against existing approaches on a standard benchmark dataset.

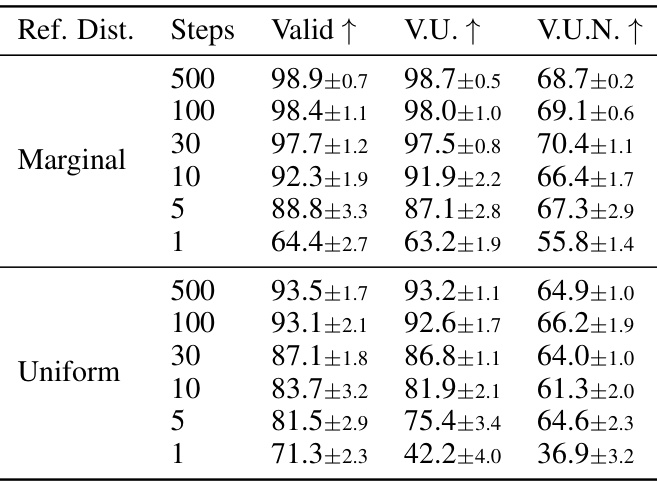
This ablation study investigates the effect of different reference distributions (marginal vs. uniform) and varying numbers of sampling steps on the performance of the DISCO model with an MPNN backbone. The results are evaluated using the metrics Valid, Unique, and Novel, showing the impact of these hyperparameters on model performance.

Full paper

#