↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world optimization problems are time-varying and safety-critical. Existing methods struggle to safely optimize these unknown time-varying systems, often relying on ad-hoc techniques or lacking theoretical guarantees. This creates a need for algorithms capable of safely tracking changing safe regions, maintaining safety while optimizing performance.
TVSAFEOPT directly addresses this. This algorithm uses a Bayesian optimization approach with a spatio-temporal kernel, enabling it to effectively model the time-varying nature of the problem. It achieves this without needing explicit change detection, providing formal safety guarantees. Furthermore, it provides optimality guarantees for the algorithm when the optimization problem becomes stationary, showcased through experiments on synthetic data and real-world case studies.
Key Takeaways#
Why does it matter?#
This paper is important because it presents TVSAFEOPT, a novel algorithm for safe time-varying Bayesian optimization. This addresses a critical need in various fields where systems evolve over time, requiring robust and safe decision-making under uncertainty. The algorithm’s ability to handle time-varying reward and safety constraints with theoretical safety and near-optimality guarantees opens new avenues for research in safe exploration and exploitation strategies in dynamic environments. It offers solutions to critical challenges in robotics, autonomous systems, and control systems, where safety is paramount.
Visual Insights#

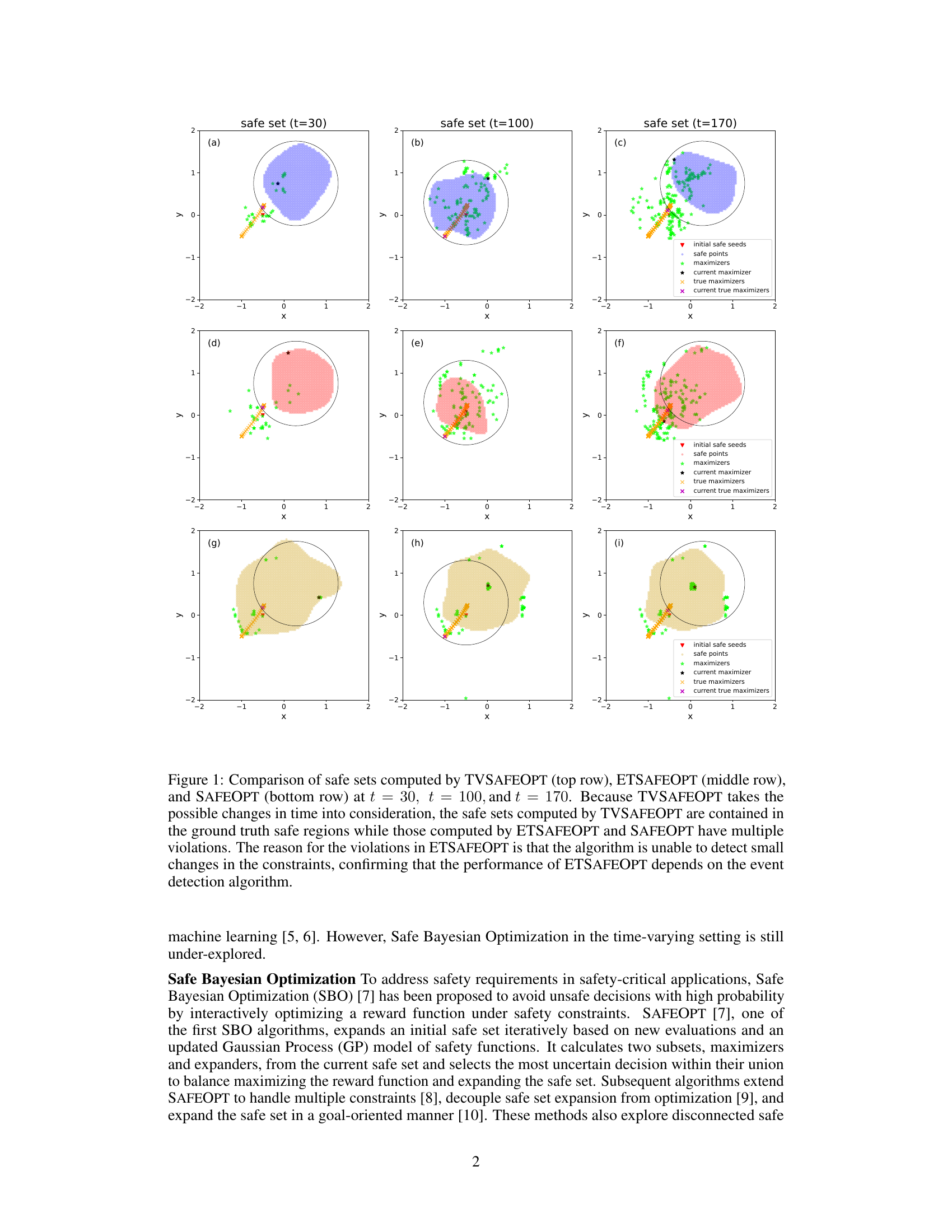
This figure compares the performance of three safe Bayesian optimization algorithms (TVSAFEOPT, ETSAFEOPT, and SAFEOPT) in handling time-varying constraints. The top row shows the safe sets identified by TVSAFEOPT at three different time points (t=30, 100, 170). The middle and bottom rows show the corresponding safe sets generated by ETSAFEOPT and SAFEOPT, respectively. The figure demonstrates that TVSAFEOPT is more effective at tracking the time-varying safe regions compared to the other two algorithms, which frequently produce safe sets that violate the true constraints due to their inability to detect small changes in the constraint functions. The figure highlights the robustness of TVSAFEOPT in handling dynamic constraints.

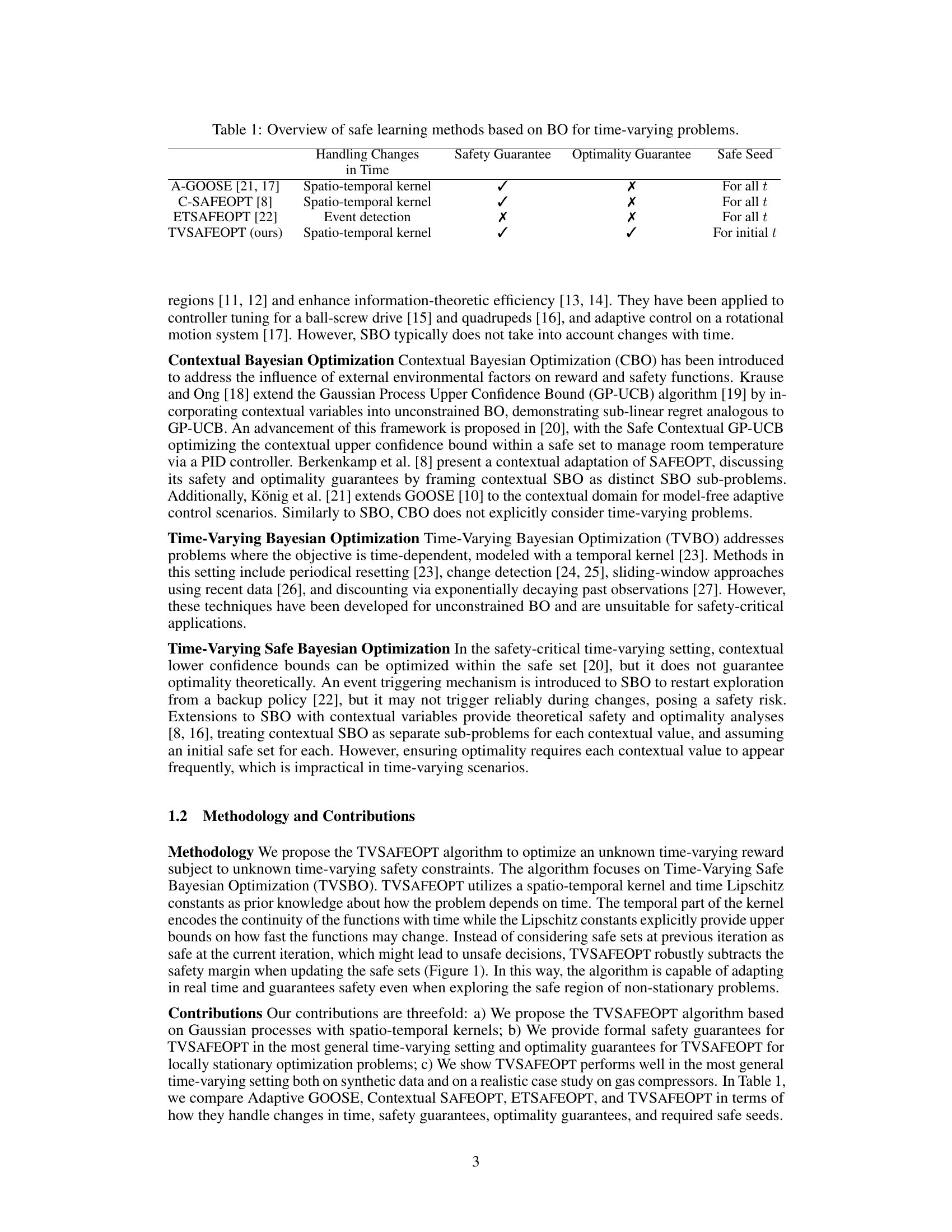
This table compares four different safe Bayesian optimization methods (A-GOOSE, C-SAFEOPT, ETSAFEOPT, and TVSAFEOPT) in terms of their ability to handle changes in time, their safety and optimality guarantees, and the type of safe seed they require. It highlights the unique spatio-temporal kernel approach of TVSAFEOPT and its improved safety and optimality properties compared to the other methods.
In-depth insights#
SafeOpt Advancements#
SafeOpt advancements represent a crucial area in robotics and autonomous systems. Early SafeOpt methods focused on iteratively expanding a safe set, but this approach struggles with time-varying constraints and optimality. Significant improvements involve incorporating spatio-temporal kernels in Gaussian processes, allowing the algorithm to model changes in the reward and safety functions over time. This dramatically improves performance in dynamic environments. Another key advancement is the integration of Lipschitz continuity, providing theoretical guarantees on the algorithm’s safety and convergence. Although optimality guarantees are often easier to establish in stationary settings, recent work extends these to near-optimality guarantees under slowly changing conditions, bridging the gap between safety and performance. Future research will likely focus on further enhancing the robustness and efficiency of these techniques, perhaps through advanced kernel designs or more sophisticated exploration strategies, while maintaining strong theoretical underpinnings.
Spatio-Temporal Kernel#
The concept of a spatio-temporal kernel is crucial for modeling data exhibiting dependencies across both space and time. In the context of this research paper, its application within Gaussian processes (GPs) is particularly noteworthy. The spatio-temporal kernel allows the GP to capture correlations between observations not only based on their spatial proximity but also on their temporal proximity. This is a significant advancement over traditional GP models which often ignore the temporal dimension, leading to more accurate predictions in time-varying systems. The choice of kernel function is critical; it directly impacts the ability of the model to capture complex spatio-temporal relationships. A well-chosen kernel ensures the GP effectively learns the underlying dynamics of the system, accommodating changes and trends over time. The effectiveness of the spatio-temporal kernel is demonstrated in the paper’s results; it enables safe and accurate optimization in dynamic environments where rewards and constraints vary across both space and time, significantly improving performance compared to models that lack this spatio-temporal awareness.
TVSAFEOPT Algorithm#
The TVSAFEOPT algorithm is a novel approach to address the challenge of safe time-varying Bayesian optimization. It builds upon existing SAFEOPT methods but incorporates a spatio-temporal kernel within the Gaussian process model. This crucial addition allows TVSAFEOPT to explicitly account for the time-varying nature of both the reward and safety functions, thus offering improved safety and adaptability in dynamic environments. Lipschitz constants further enhance the algorithm’s robustness by providing bounds on how quickly the reward and safety functions can change over time. Importantly, TVSAFEOPT avoids the need for explicit change detection, offering a more seamless and robust adaptation to shifting conditions. The algorithm also incorporates mechanisms for safe exploration and exploitation, balancing the need for maximizing rewards and expanding the safe operational region. Its key contribution lies in offering theoretical guarantees for safety, alongside near-optimality guarantees under specific conditions. This combination of practical advantages and theoretical underpinnings make TVSAFEOPT a valuable tool for numerous real-world applications, especially in safety-critical settings.
Safety Guarantees#
The concept of safety guarantees in the context of a research paper on time-varying optimization is crucial. It signifies the algorithm’s ability to reliably avoid unsafe decisions throughout the optimization process, especially when dealing with unknown and potentially time-varying reward and safety functions. The core of safety guarantees lies in providing high-probability bounds on the safety constraints, meaning the algorithm assures the constraints will be satisfied with a demonstrably high level of certainty. This usually involves the use of confidence intervals and probabilistic reasoning. Spatio-temporal kernels are likely employed to capture the time-varying aspects of the problem and provide accurate predictions, allowing the algorithm to account for dynamic changes in the environment. The effectiveness of the safety guarantees hinges on the assumptions made about the nature of the problem (e.g., Lipschitz continuity), the choice of kernel, and the parameters used in the algorithm. A successful presentation of safety guarantees needs to formally prove that the safety constraints are satisfied with a user-specified probability. Rigorous mathematical proofs are essential to establish the reliability of the safety guarantees. In the context of a research paper, this typically includes lemmas and theorems, demonstrating both the theoretical underpinnings and the practical feasibility of achieving safe optimization.
Future of TVSBO#
The future of Time-Varying Safe Bayesian Optimization (TVSBO) is bright, promising advancements in various safety-critical applications. Addressing the limitations of current TVSBO methods, such as the reliance on Lipschitz constants and the trade-off between safety and optimality, will be crucial. Future research should explore alternative approaches to handle time-varying functions and constraints, possibly leveraging techniques from online learning and robust optimization. Developing more efficient methods for handling high-dimensional spaces and large datasets is also critical. Furthermore, investigating the theoretical properties of TVSBO under more realistic assumptions, such as non-stationary noise and model misspecification, is necessary. Real-world applications will greatly benefit from improved scalability and robustness of TVSBO algorithms. Incorporating advanced deep learning models for better function approximation, combined with efficient uncertainty quantification, is an exciting area for exploration. Finally, exploring the potential of TVSBO in conjunction with other advanced control strategies will open doors to next-generation control systems with enhanced safety and performance guarantees.
More visual insights#
More on figures

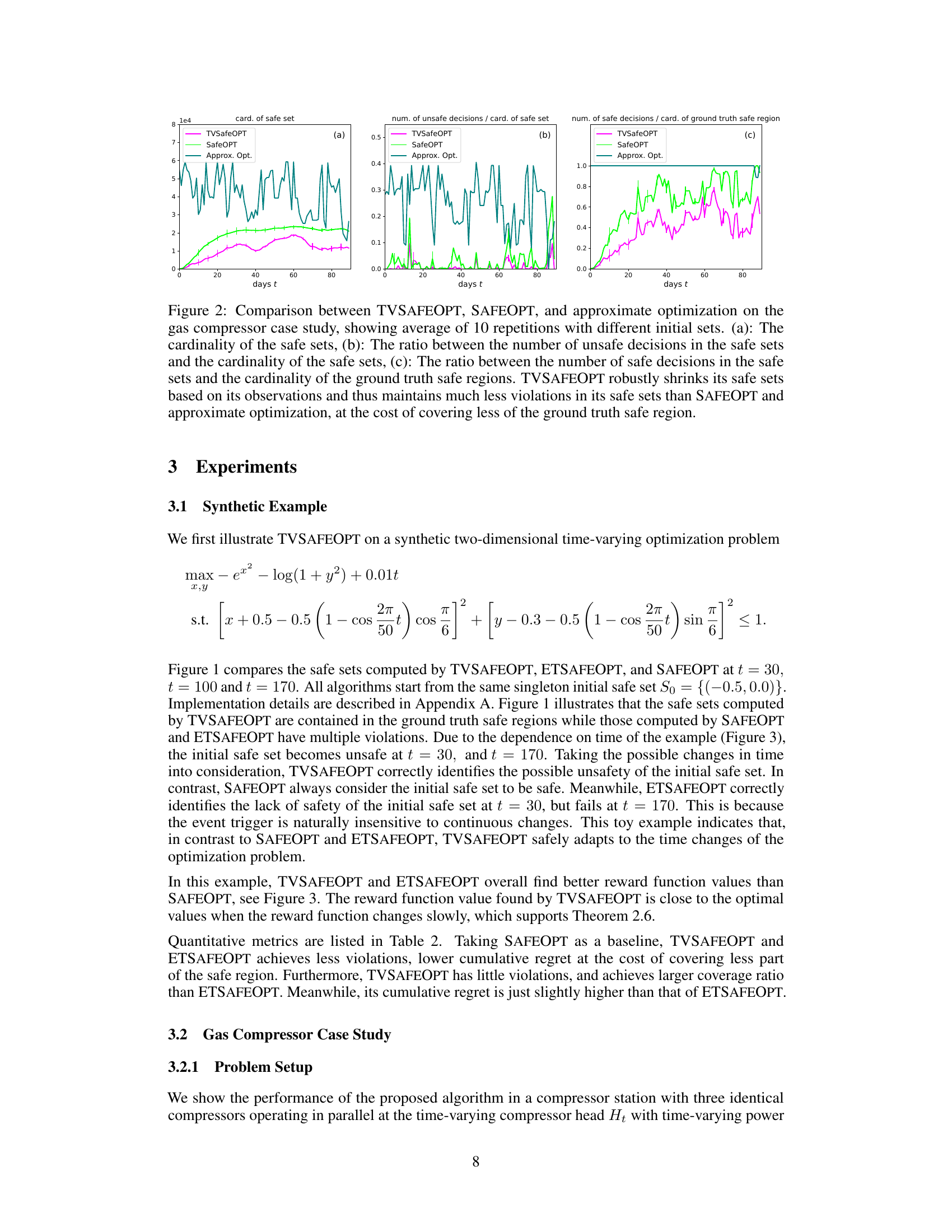
This figure compares the performance of TVSAFEOPT, SAFEOPT, and approximate optimization methods on a gas compressor case study. It shows the cardinality of safe sets, the ratio of unsafe decisions to the cardinality of safe sets, and the ratio of safe decisions to the cardinality of the ground truth safe region over 80 days. TVSAFEOPT demonstrates fewer violations and less unsafe decisions than the other two methods, but at the cost of a reduced coverage of the true safe region.

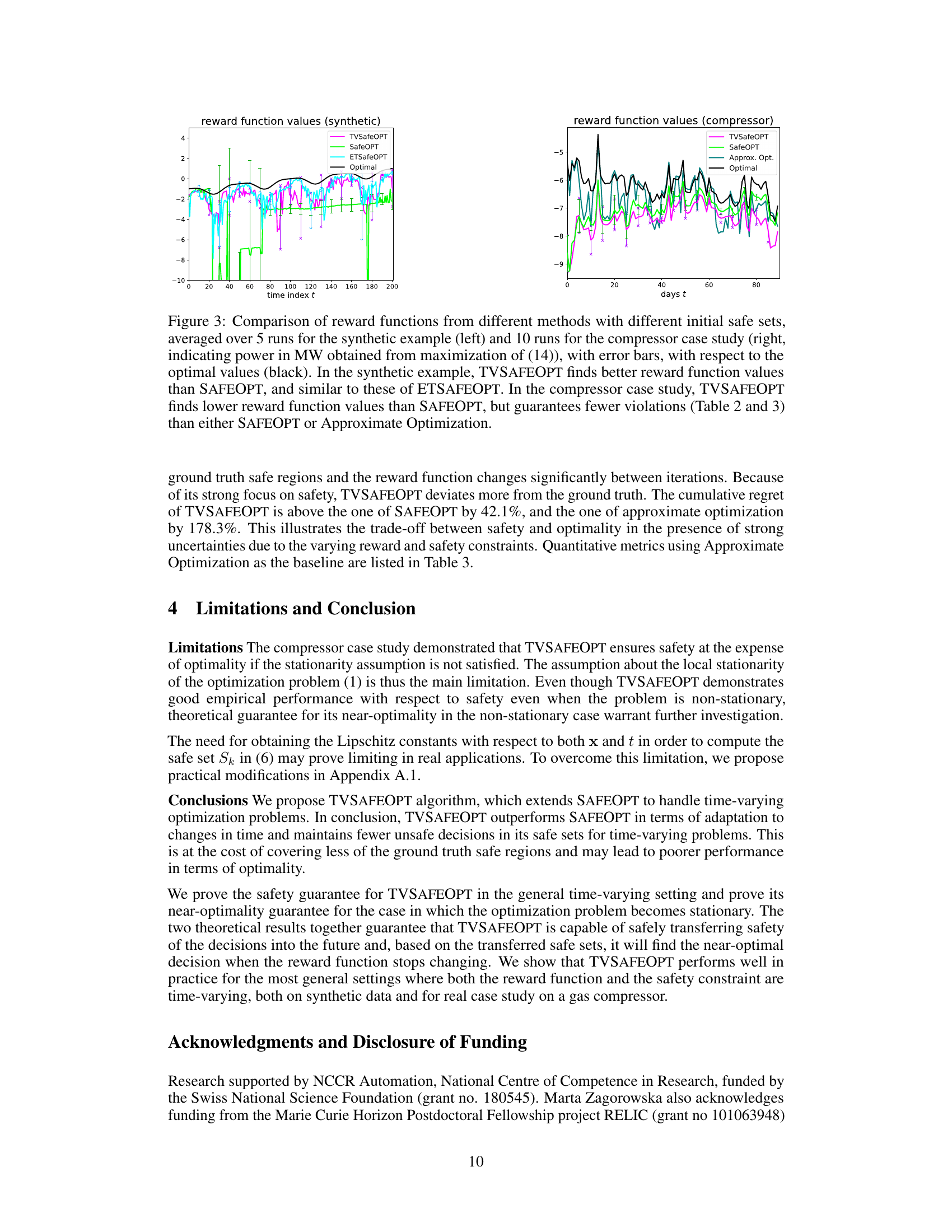
This figure compares the reward functions obtained by different optimization methods (TVSAFEOPT, SAFEOPT, ETSAFEOPT, and Approximate Optimization) across two different case studies (synthetic example and gas compressor). The left panel shows the synthetic case study, demonstrating TVSAFEOPT achieves better results compared to SAFEOPT and similar results to ETSAFEOPT. The right panel shows the gas compressor study and reveals that TVSAFEOPT achieves lower rewards than SAFEOPT but maintains superior safety, incurring less violations compared to the others. Error bars illustrate the variability of the results.

This figure compares the reward function values obtained by TVSAFEOPT, SAFEOPT, ETSAFEOPT, and approximate optimization methods over time for both a synthetic example and a real-world gas compressor case study. The left panel shows the synthetic results, indicating that TVSAFEOPT performs comparably to ETSAFEOPT and better than SAFEOPT. The right panel displays the compressor case study results, where TVSAFEOPT achieves lower reward but significantly fewer safety violations compared to the other methods. Error bars are included.

This figure compares the performance of three safe Bayesian optimization algorithms (TVSAFEOPT, ETSAFEOPT, and SAFEOPT) in a time-varying setting. The top row shows the safe sets identified by TVSAFEOPT at three different time points (t=30, t=100, t=170). The middle and bottom rows show the safe sets for ETSAFEOPT and SAFEOPT respectively, at the same time points. The figure demonstrates that TVSAFEOPT is better at adapting to changes in the safe region over time, unlike the other two algorithms. The difference is because TVSAFEOPT takes time-varying nature into account in its computation.
This figure compares the performance of three safe Bayesian optimization algorithms (TVSAFEOPT, ETSAFEOPT, and SAFEOPT) in handling time-varying optimization problems. The algorithms are tested on a synthetic dataset, and the plots show the safe sets estimated by each algorithm at three different time points (t=30, t=100, t=170). TVSAFEOPT consistently produces safe sets that are entirely contained within the ground truth safe regions, demonstrating its robustness to time variations. In contrast, ETSAFEOPT and SAFEOPT show multiple violations of the safety constraints, highlighting their limitations in accurately tracking changes in the safe region over time.
More on tables

This table presents a comparison of three Bayesian Optimization algorithms: TVSAFEOPT, ETSAFEOPT, and SAFEOPT. The comparison is based on three metrics: Violations (percentage of unsafe decisions made within the safe sets), Coverage Ratio (percentage of safe decisions within the ground truth safe region), and Cumulative Regret (a measure of the cumulative difference between the reward obtained by each method and the optimal reward). The results are averages and standard deviations from five independent runs, each starting with a different randomly selected initial safe set.

This table compares the performance of TVSAFEOPT and SAFEOPT against a simple approximate optimization method in a realistic case study involving gas compressors. The results are averaged over 10 runs with varying initial safe sets. Key metrics include the percentage of violations, the coverage ratio (how well the safe set covers the true safe region), and cumulative regret (performance compared to the optimum). ETSAFEOPT is excluded because its performance heavily relies on event detection which is not applicable to this study’s compressor degradation.
Full paper#