The Poisson Midpoint Method for Langevin Dynamics: Provably Efficient Discretization for Diffusion Models

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in machine learning and AI, particularly those working on diffusion models and sampling algorithms. It offers a provably efficient method that significantly speeds up the image generation process, reducing computational costs while maintaining high-quality output. This opens new avenues for research in optimizing sampling techniques and developing more efficient generative models, impacting various applications.

Visual Insights

#

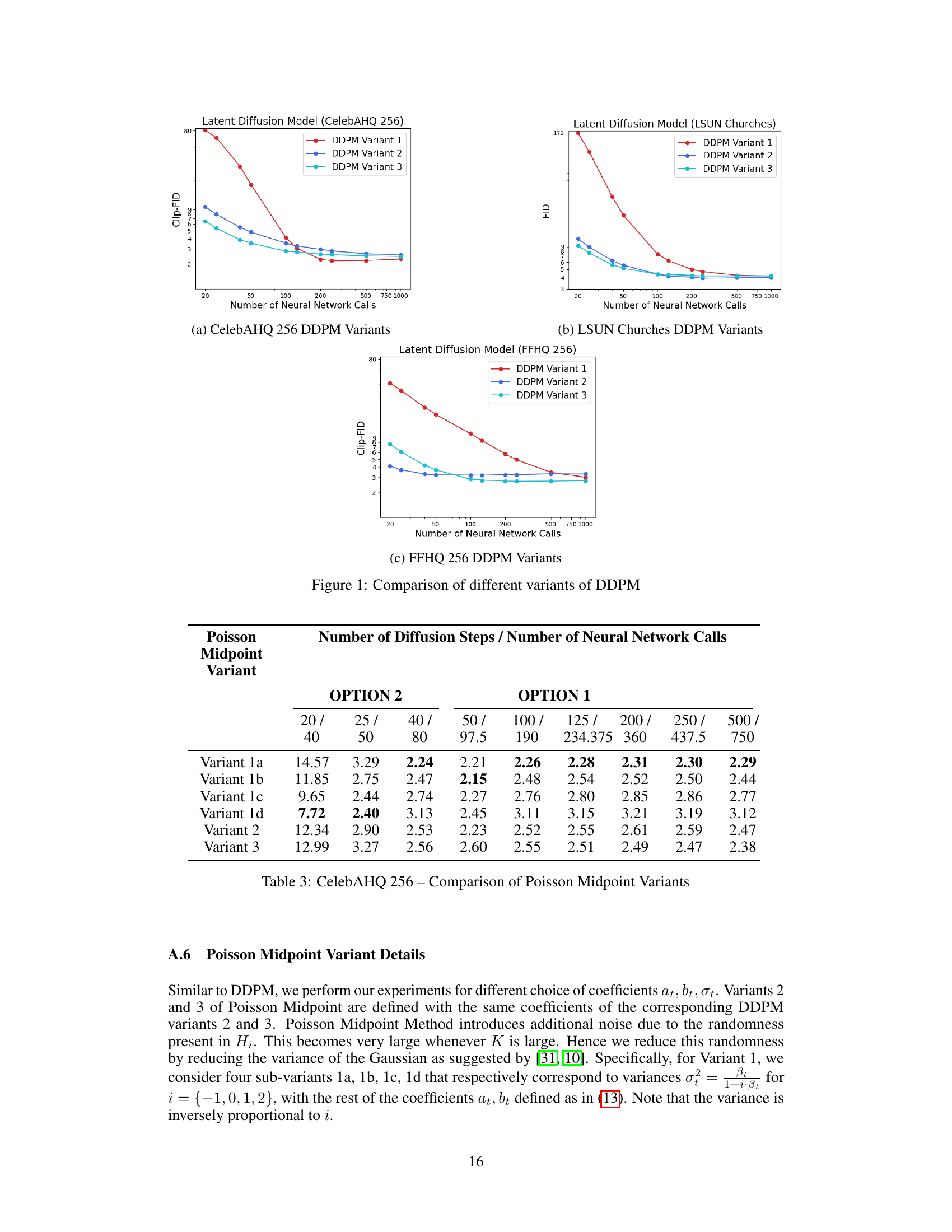
This figure compares the performance of three different DDPM variants across four datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256) in terms of Clip-FID or FID scores. The x-axis represents the number of neural network calls, and the y-axis shows the FID or Clip-FID score. Each line corresponds to a specific DDPM variant, demonstrating the variability in performance depending on the chosen coefficients and the dataset. The figure highlights the impact of different DDPM implementations on the quality of generated images. The results suggest that optimal variants differ depending on the dataset and the desired number of steps.

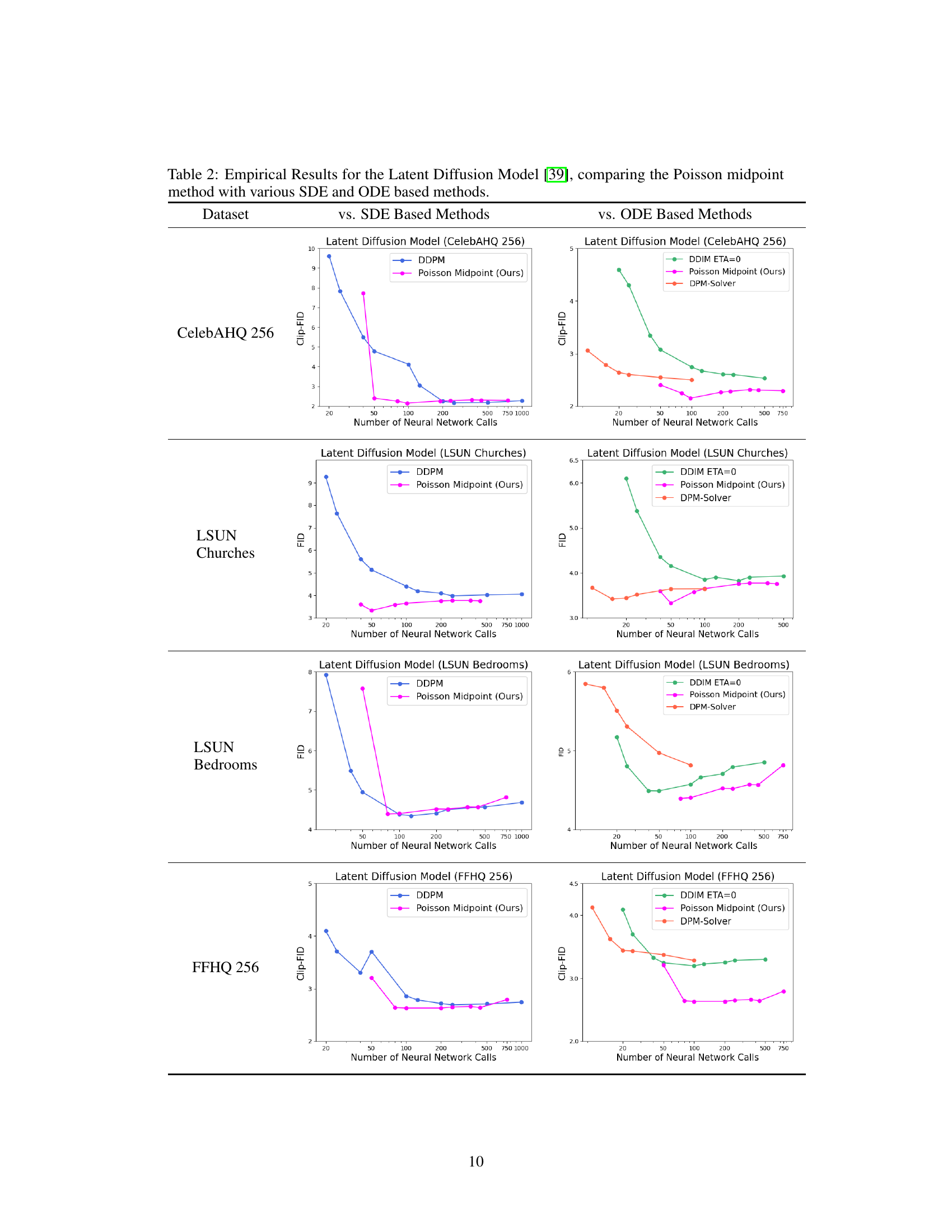
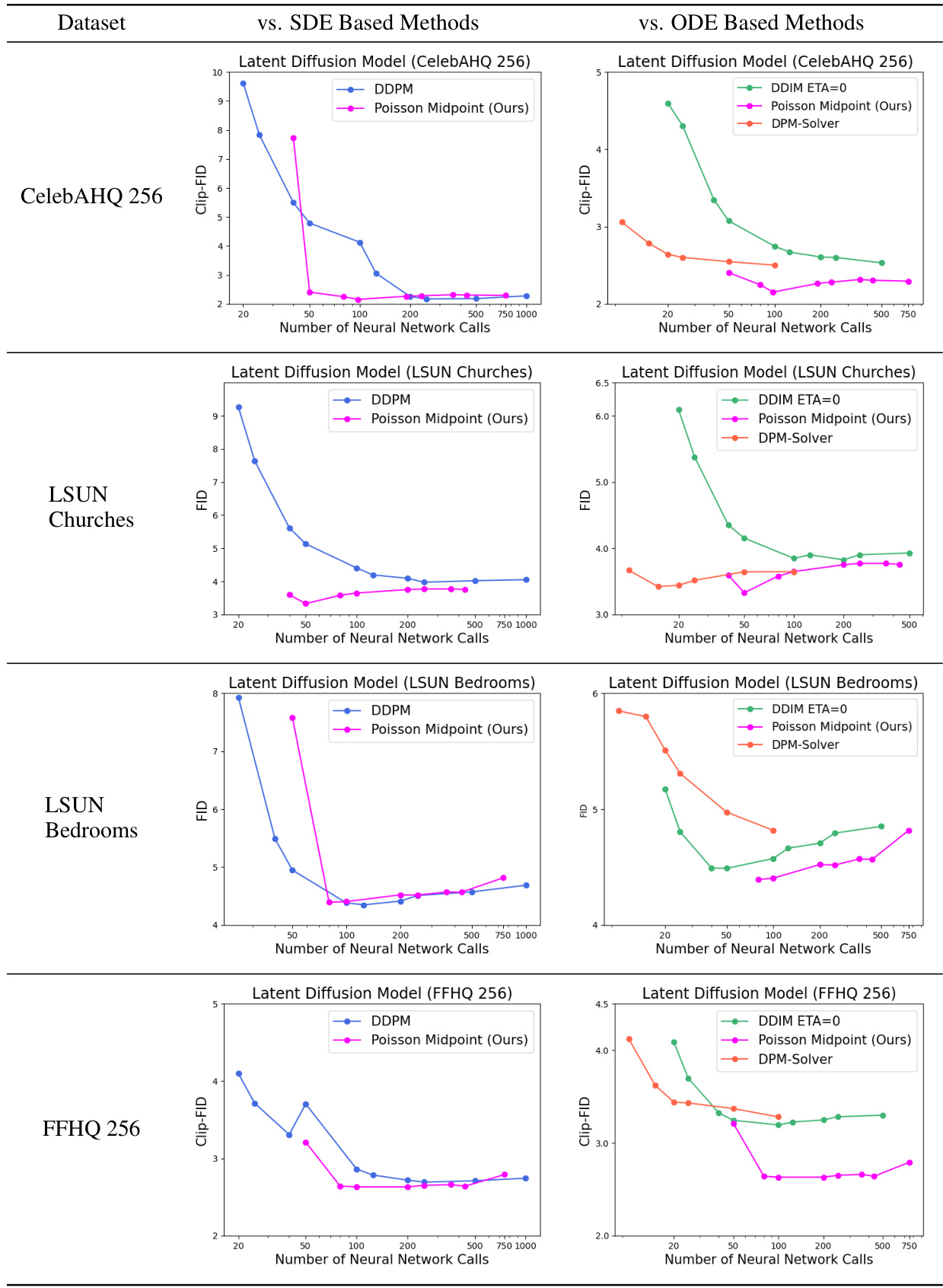
This table presents empirical results comparing the Poisson Midpoint Method (a novel method proposed in the paper) against other established methods (DDPM, DDIM, and DPM-Solver) for generating images using Latent Diffusion Models. The comparison is made across four different datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256). The table shows the FID (Fréchet Inception Distance) or Clip-FID scores (depending on the dataset) achieved by each method, varying the number of neural network calls (a measure of computational cost). This allows for assessing the trade-off between image quality and computational efficiency for different approaches.

In-depth insights

#

Poisson Midpoint

#

The Poisson Midpoint method, a novel approach to Langevin Dynamics discretization, offers a provably efficient alternative to traditional Euler-Maruyama methods. By cleverly approximating multiple small-step updates with a single larger-step update, it achieves a quadratic speedup under weak assumptions. This is particularly beneficial for computationally expensive applications like diffusion models, where numerous iterations are crucial. Unlike prior midpoint methods, Poisson Midpoint’s theoretical guarantees extend beyond strongly log-concave distributions, handling non-log concave densities and time-varying drifts. The core of the method’s efficiency lies in its stochastic approximation of multiple LMC steps, reducing bias while maintaining accuracy. Empirical evaluations confirm significant computational gains and performance improvements over competing techniques, particularly in the context of diffusion models for image generation.

Diffusion Models

#

Diffusion models are a class of generative models that synthesize data by gradually adding noise to a data sample and then reversing the process to generate new samples. The paper explores these models within the context of Langevin dynamics, a stochastic differential equation used for sampling from probability distributions. A key aspect is the time discretization of Langevin dynamics, where the continuous-time process is approximated as a sequence of discrete steps. The authors focus on the efficiency of discretization, noting that straightforward methods like the Euler-Maruyama method can be computationally expensive. The paper proposes and analyzes a novel discretization technique – the Poisson Midpoint Method – showing it to be significantly more efficient than existing methods such as the Euler-Maruyama method, especially when applied to diffusion models. This method is theoretically proven to have a quadratic speed-up under very weak assumptions. The improved efficiency is demonstrated empirically via experiments involving image generation, where the method is shown to match the quality of high-step methods (e.g., 1000 steps) with far fewer steps, offering a substantial computational advantage. The results are evaluated over several datasets including CelebAHQ, LSUN Churches, LSUN Bedrooms, and FFHQ.

Quadratic Speedup

#

The heading ‘Quadratic Speedup’ highlights a significant finding: the Poisson Midpoint Method (PMM) achieves a quadratic improvement in computational efficiency compared to standard Langevin Monte Carlo (LMC) methods. This speedup isn’t merely incremental; it’s a substantial leap, especially crucial for computationally expensive applications like diffusion models. The analysis reveals that under specific conditions (the target distribution satisfying Logarithmic Sobolev Inequalities), PMM’s convergence rate is demonstrably superior. The quadratic speedup is not universally guaranteed, however; it’s contingent on the target distribution and the assumptions made. The theoretical results are supported by empirical evidence, showing significant gains in image generation tasks. Nonetheless, the analysis reveals limitations, particularly in scenarios where the assumptions don’t perfectly hold, or when the compute budget is exceedingly small. The method’s practical applicability is validated through its superior performance on multiple datasets compared to other state-of-the-art methods, thereby further highlighting its significance.

Empirical Results

#

The Empirical Results section of a research paper is crucial for validating theoretical claims. It should present results from experiments designed to test the paper’s core hypotheses. A strong Empirical Results section will include clear visualizations, such as graphs showing performance metrics across different conditions. Quantitative measures of performance, such as FID (Fréchet Inception Distance) scores or other relevant metrics, should be reported alongside the visualizations, providing a robust comparison across different methods or settings. Error bars or confidence intervals are also crucial for indicating the statistical significance of the results and showing the reliability of the findings. The discussion of the results should be insightful, exploring both the successes and limitations of the proposed approach. A detailed analysis of the results, explaining unexpected outcomes or discrepancies from the hypotheses, is necessary to build credibility. Furthermore, a comparison with prior work is essential for contextualizing the results and emphasizing the novelty and contributions of the research. In short, the Empirical Results section must provide strong quantitative evidence that is comprehensively analyzed to support the paper’s central claims and provide a thorough evaluation of the proposed method against appropriate baselines and existing state-of-the-art approaches.

Future Work

#

The paper’s ‘Future Work’ section would ideally delve into several promising directions. Extending the Poisson Midpoint Method (PMM) to handle more complex scenarios such as those involving non-log-concave distributions with time-varying drift is crucial. A theoretical exploration into the convergence rates under weaker assumptions like Poincare inequalities or Holder continuity of the gradient, moving beyond the current Logarithmic Sobolev Inequality (LSI) framework, would enhance the method’s applicability. Investigating the method’s performance for high-dimensional problems while maintaining efficiency is another key area. This could involve optimizing the method for specific hardware architectures and datasets. Finally, a deeper empirical evaluation on diverse tasks beyond image generation, and a more comprehensive comparison with other state-of-the-art sampling techniques, would provide a complete assessment of PMM’s strengths and limitations. Specifically, investigating the method’s robustness to noisy estimations of the gradient is important for practical applications.

More visual insights

#

More on figures

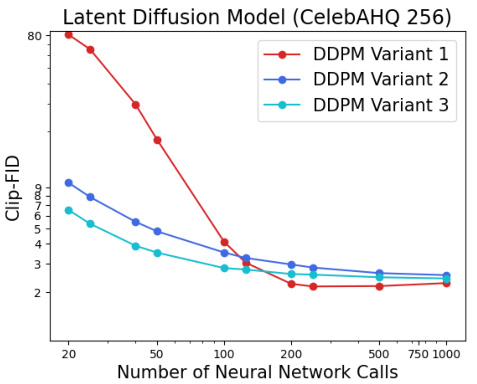
The figure compares the performance of three different variants of the DDPM (Denoising Diffusion Probabilistic Models) scheduler across different numbers of neural network calls. Each variant uses different coefficient choices (at, bt, σt) within the DDPM framework. The x-axis represents the number of neural network calls, while the y-axis represents the CLIP-FID (CLIP-based Fréchet Inception Distance) score, a metric used to evaluate the quality of generated images. Lower CLIP-FID scores indicate higher quality. The plots show how the quality of generated images changes for each DDPM variant as the computational cost (number of neural network calls) varies. This comparison helps understand the impact of coefficient choices on the efficiency and image quality of DDPM.

This figure compares the performance of three different DDPM variants across various datasets (CelebAHQ 256, LSUN Churches, FFHQ 256) by plotting the FID score against the number of neural network calls. Each line represents a different DDPM variant, showcasing how their performance changes with varying computational budgets. The purpose is to demonstrate the impact of different DDPM implementations on the quality of generated images.

This figure compares the performance of three different DDPM (Denoising Diffusion Probabilistic Models) variants across three different datasets: CelebAHQ 256, LSUN Churches, and FFHQ 256. Each subplot shows the Clip-FID (Fréchet Inception Distance) score plotted against the number of neural network calls. Different lines in the plots represent different DDPM variants. The figure highlights the variability in performance between DDPM variants and across datasets, which motivates the need for a robust and consistent scheduler like the one introduced in the paper.

More on tables

This table presents the empirical results comparing the performance of the Poisson Midpoint Method against other SDE and ODE-based methods for image generation using the Latent Diffusion Model. The results are shown for four different datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256). For each dataset, the table shows the FID (Fréchet Inception Distance) or Clip-FID scores for different numbers of neural network calls, which represents the computational cost. The table compares the Poisson Midpoint method with various DDPM (Denoising Diffusion Probabilistic Models) variants, DDIM (Denoising Diffusion Implicit Models), and DPM-Solver methods. The goal is to demonstrate that the Poisson Midpoint Method achieves comparable or better sample quality with significantly fewer neural network calls compared to other methods.

This table presents the empirical results comparing the performance of the proposed Poisson Midpoint Method against other SDE (Stochastic Differential Equation) and ODE (Ordinary Differential Equation) based methods for image generation using the Latent Diffusion Model. The table shows the FID (Fréchet Inception Distance) or CLIP-FID scores for different datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256) across varying numbers of neural network calls. Lower FID/CLIP-FID scores indicate better image quality. The comparison highlights the efficiency of the Poisson Midpoint Method in achieving similar or better image quality with significantly fewer neural network calls compared to other methods.

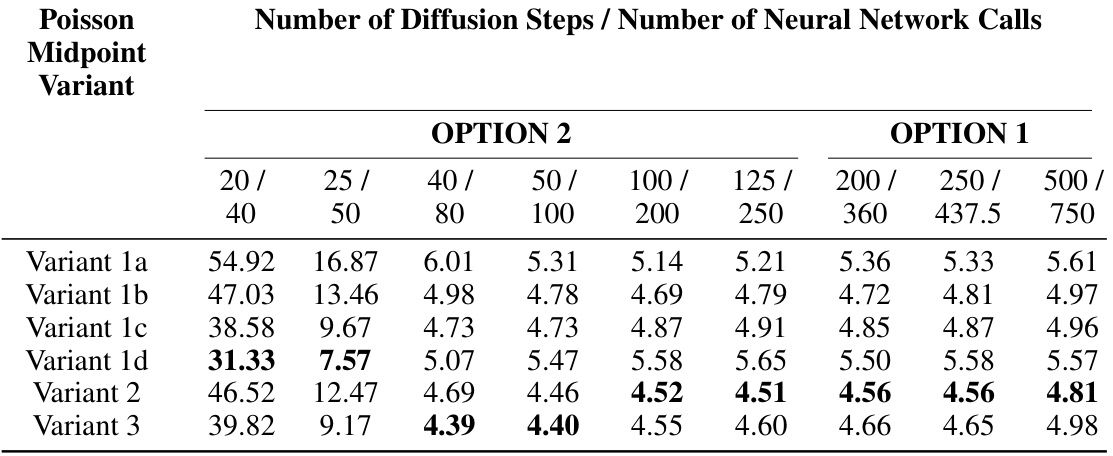
This table presents the empirical results obtained by applying the Poisson Midpoint Method and comparing it with several SDE and ODE-based methods on four datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256). For each dataset, it shows the FID or Clip-FID scores for different methods, varying the number of neural network calls. The results demonstrate the performance of the proposed method against state-of-the-art alternatives, highlighting its ability to maintain high sample quality with fewer computational steps.

This table presents the empirical results obtained by applying the Poisson midpoint method, various SDE-based methods (including different DDPM variants), and ODE-based methods (DDIM and DPM-Solver) to the latent diffusion model for four different datasets: CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256. The results are presented in terms of FID (Fréchet Inception Distance) and Clip-FID (CLIP-based FID), which measure the sample quality, across a range of neural network calls (indicative of computational cost). The table allows for comparison of the Poisson midpoint method against existing state-of-the-art methods in terms of sample quality versus computational efficiency.

This table presents the empirical results comparing the performance of the Poisson Midpoint Method against other SDE and ODE based methods for image generation using the Latent Diffusion Model. The comparison is done across four different datasets: CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256. The table shows the FID (Fréchet Inception Distance) or Clip-FID scores for different numbers of neural network calls (reflecting computational cost). Lower FID/Clip-FID scores indicate better image quality. The results demonstrate how the Poisson Midpoint Method achieves comparable or better image quality with significantly fewer neural network calls compared to other methods.

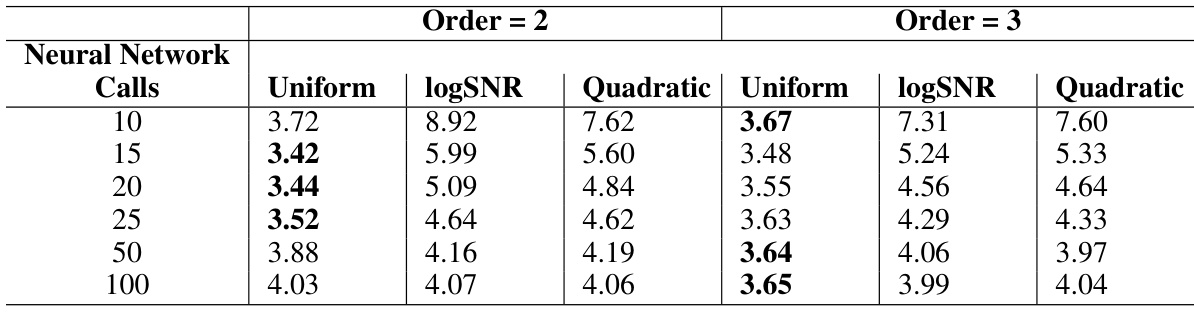
This table compares the FID (Fréchet Inception Distance) and CLIP-FID scores achieved by the Poisson Midpoint Method against several other SDE (Stochastic Differential Equation) and ODE (Ordinary Differential Equation) based methods for generating images using the Latent Diffusion Model. The comparison is made across four datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256) and varying numbers of neural network calls (which corresponds to the number of steps in the algorithms). Lower FID/CLIP-FID scores indicate better image quality. The table allows assessing the performance of the Poisson Midpoint Method relative to established approaches and highlights its ability to maintain or surpass image quality with fewer computational steps.

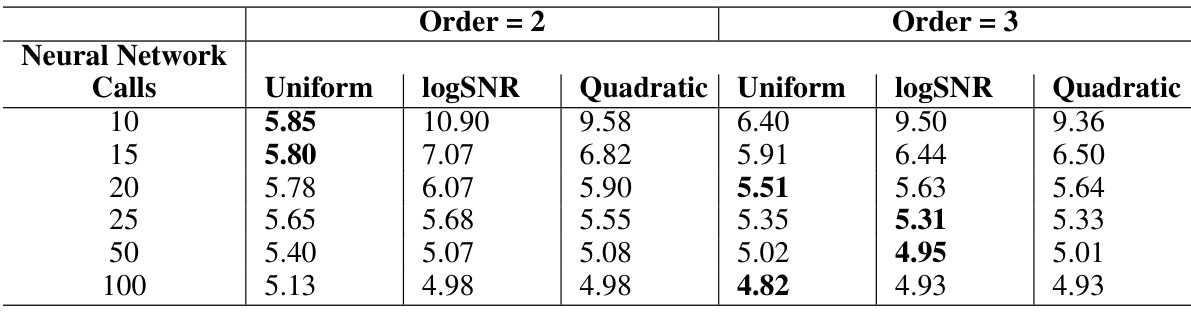
This table presents the empirical results of the Poisson Midpoint Method against established methods such as DDPM, DDIM, and DPM-Solver. The results are evaluated using FID and Clip-FID metrics for four different datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, and FFHQ 256) by generating 50k images for each method. The number of neural network calls is varied to compare the sample quality across different computational costs. The table visually shows the FID and Clip-FID scores for each dataset and method across different numbers of neural network calls, allowing for a comparison of sample quality and computational efficiency.

This table presents the empirical results of the Poisson Midpoint Method against other state-of-the-art methods for image generation using diffusion models. It compares the performance using two metrics: FID (Fréchet Inception Distance) and Clip-FID. The comparison is done across four different datasets (CelebAHQ 256, LSUN Churches, LSUN Bedrooms, FFHQ 256) and varying numbers of neural network calls. The table visually shows the FID/Clip-FID score for each method (DDPM, DDIM, DPM-Solver, and the proposed Poisson Midpoint Method) as the number of neural network calls increases, allowing for a direct performance comparison.

Full paper

#