↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Universal online learning aims to achieve regret guarantees without prior knowledge of function curvature. This is a challenging problem, especially when considering gradient variations. Existing methods often struggle with suboptimal regret bounds or lack efficiency.
This paper introduces a novel, simple, and efficient algorithm that achieves optimal gradient-variation regret for strongly convex, exp-concave, and convex functions. It uses a two-layer ensemble structure with only one gradient query per round and O(log T) base learners. The key innovation lies in a novel analysis overcoming the difficulty of controlling algorithmic stability, using linearization and smoothness properties.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in online convex optimization and related fields. It presents a simple and efficient algorithm achieving optimal regret bounds for universal online learning, addressing a long-standing open problem. This opens avenues for further research into adaptivity, efficiency, and applications to various scenarios like multi-player games.
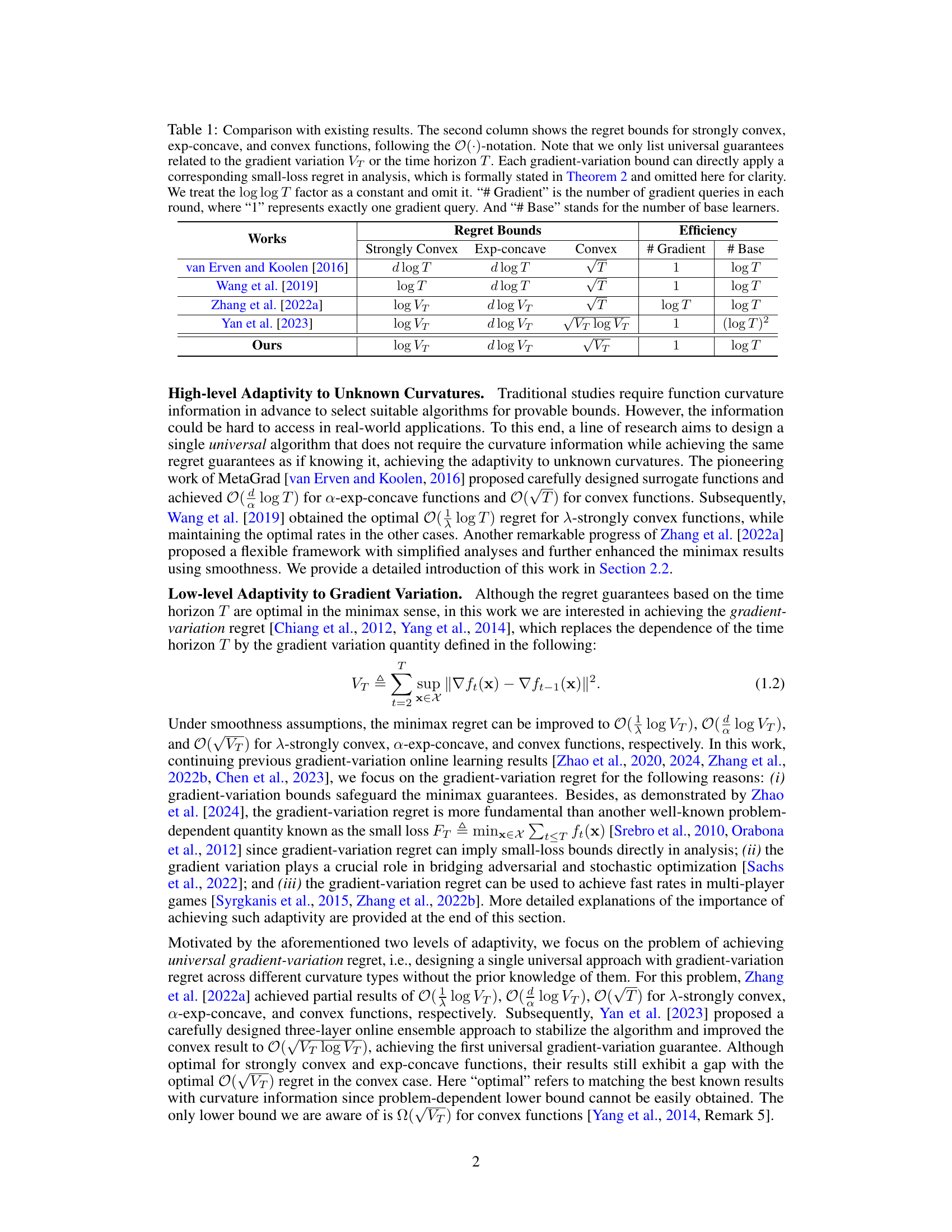
Visual Insights#

This table compares the proposed algorithm with existing algorithms in terms of regret bounds and efficiency. The regret bounds are shown for three types of functions (strongly convex, exp-concave, and convex). Efficiency is measured by the number of gradient queries per round and the number of base learners used.
Full paper#