↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
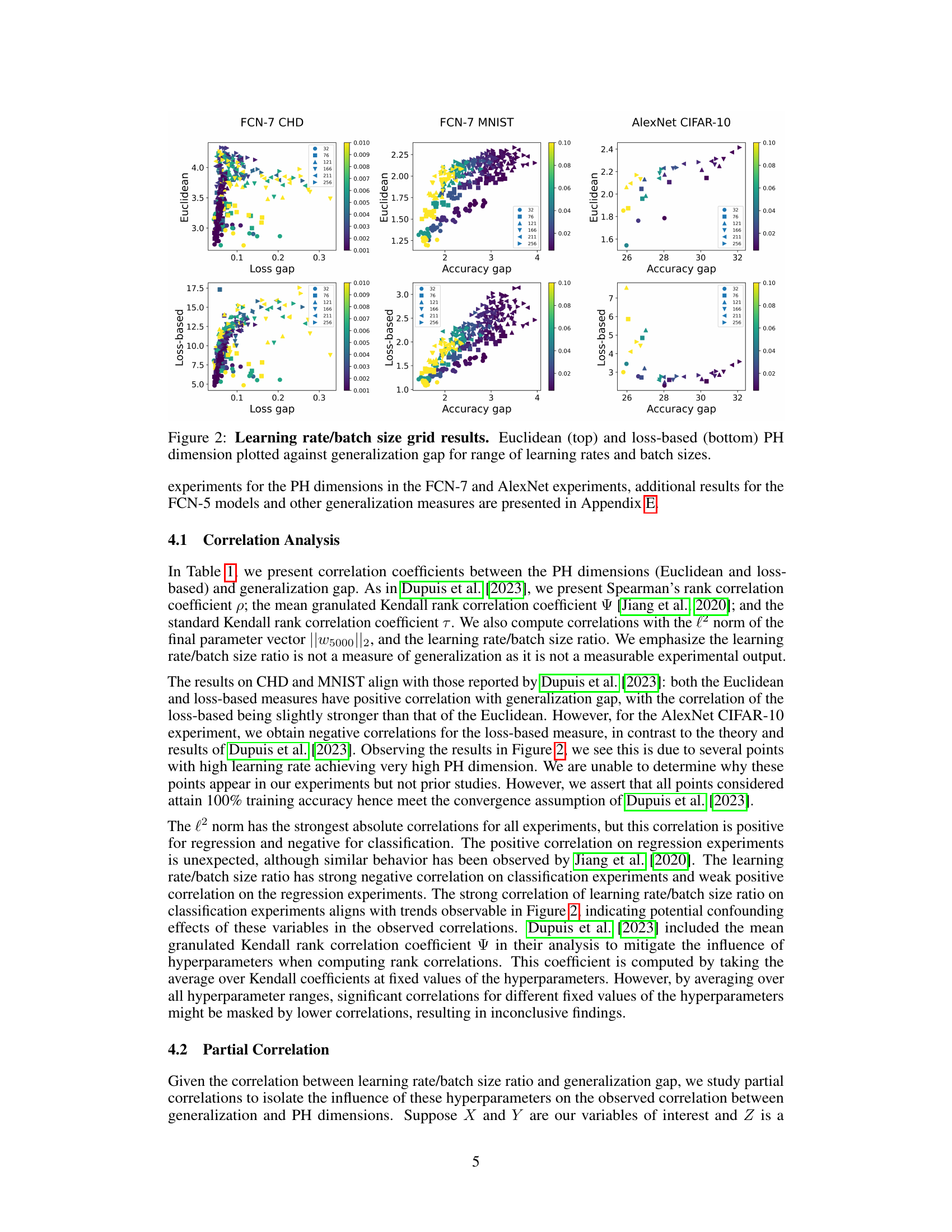
Overparameterized neural networks generalize well despite theoretical predictions, motivating research into alternative generalization measures. Recent studies use fractal dimension of optimization trajectories, particularly persistent homology dimension, to estimate generalization. However, this correlation is not always reliable.
This paper empirically evaluates these persistent homology-based measures. It finds that the correlation between topological measures and generalization is affected by hyperparameters and fails with poor model initializations. The study also observes model-wise double descent in these topological measures. This research highlights the limitations of current topological approaches and suggests further exploration of causal relationships between fractal geometry, topology, and neural network optimization.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the prevailing assumption that fractal dimension reliably predicts neural network generalization. By revealing confounding factors and failure modes, it prompts deeper investigation into the complex relationship between geometry, topology, and neural network optimization, potentially leading to more accurate generalization bounds and improved model training strategies. It also highlights the limitations of current topological measures and opens new research avenues for exploring more robust and reliable methods.
Visual Insights#
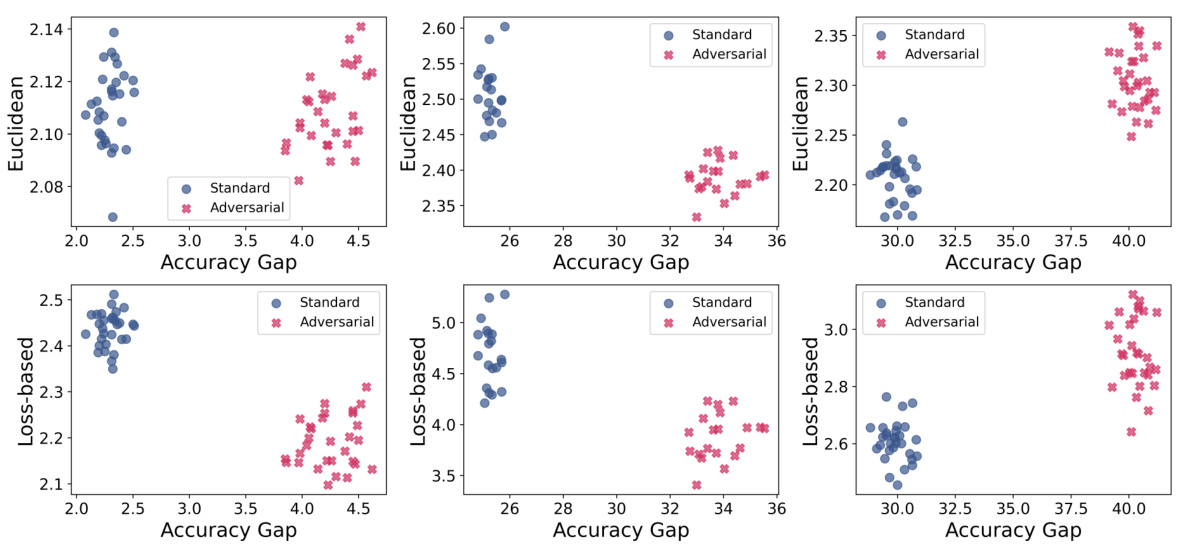
This figure shows the impact of adversarial initialization on the performance of persistent homology (PH) dimension-based generalization measures. It compares models trained with standard random initialization versus those initialized adversarially. The results reveal that adversarially initialized models exhibit a larger accuracy gap (the difference between training and test accuracy), indicating poorer generalization. Furthermore, the PH dimensions (both Euclidean and loss-based) fail to accurately reflect this poor generalization, assigning them similar or even lower dimensions compared to the randomly initialized models. This highlights a limitation of using PH dimensions as a measure of generalization in scenarios with adversarial initializations.
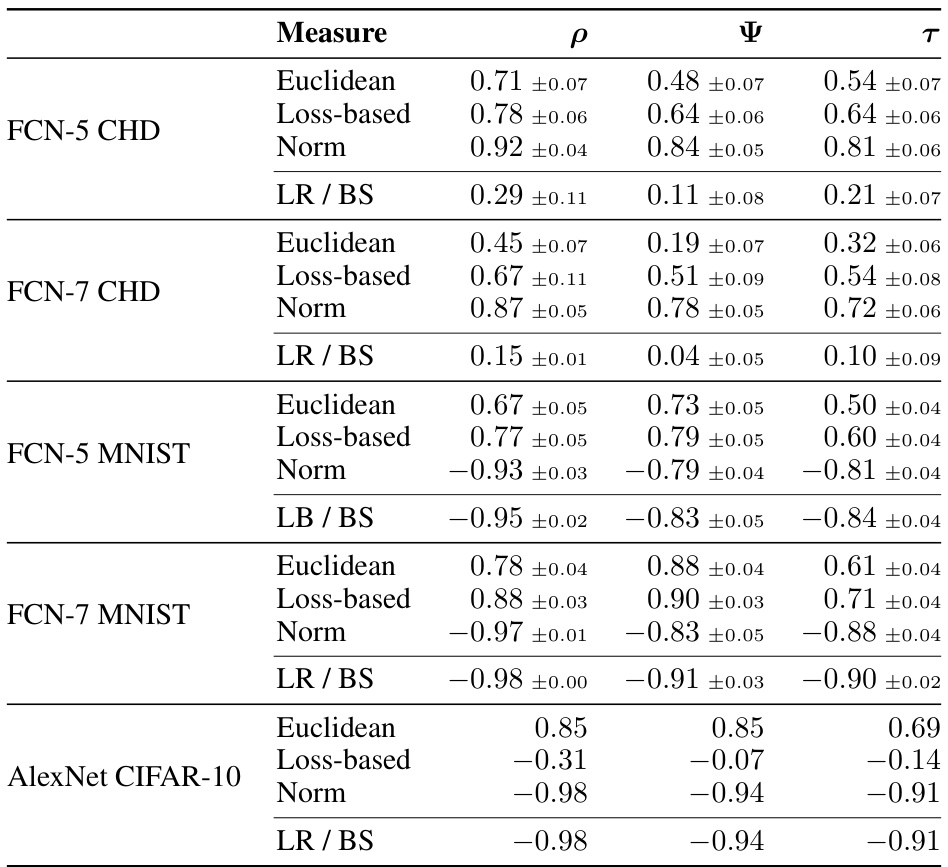
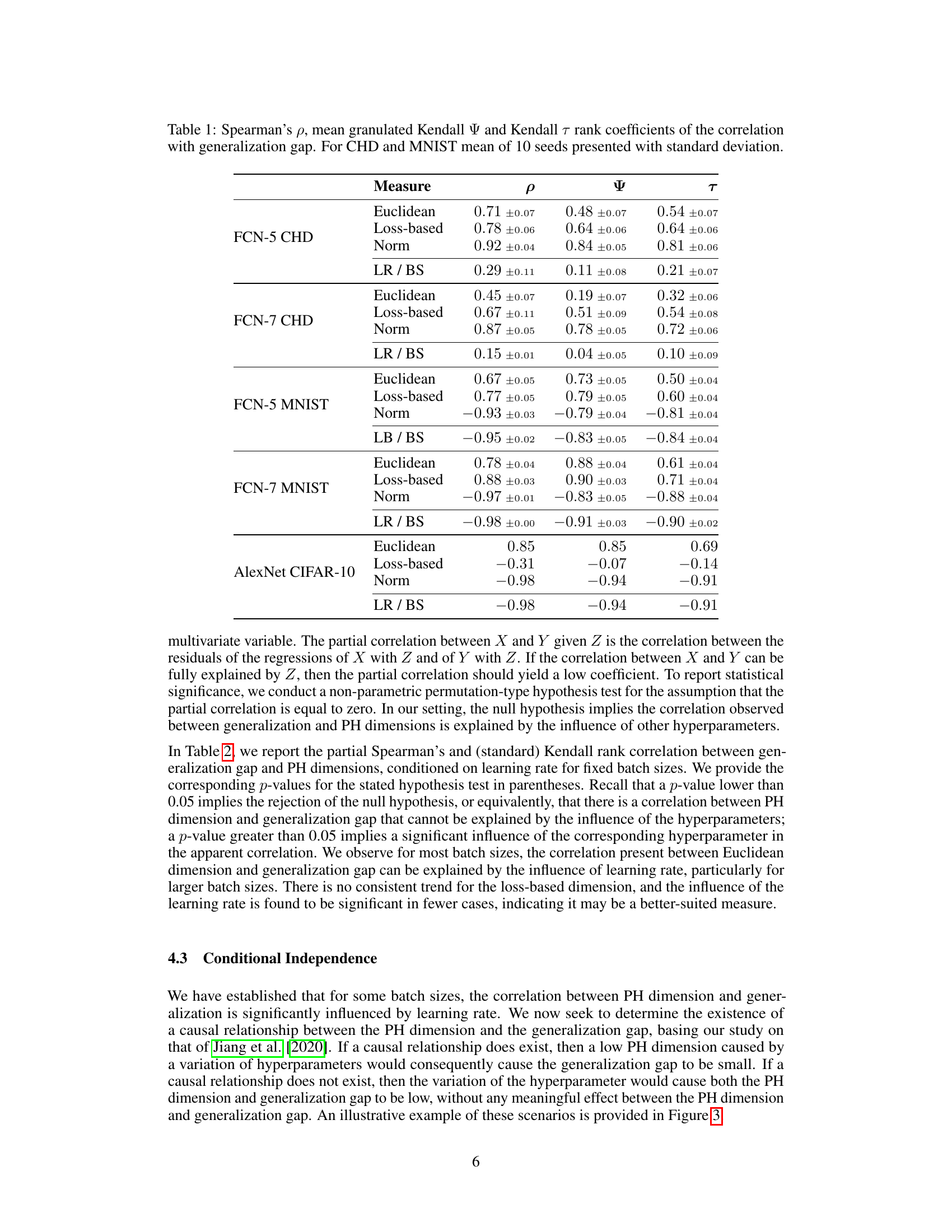
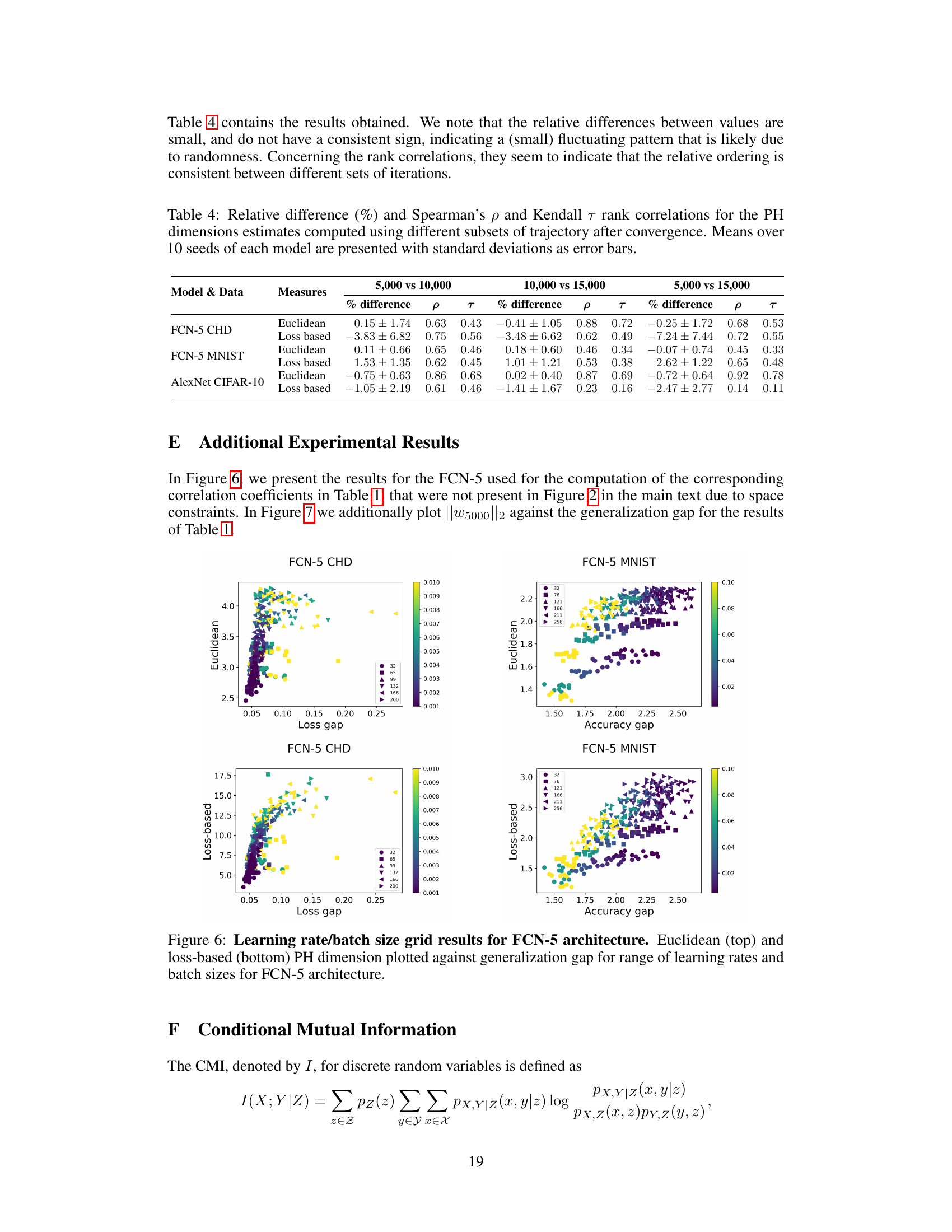
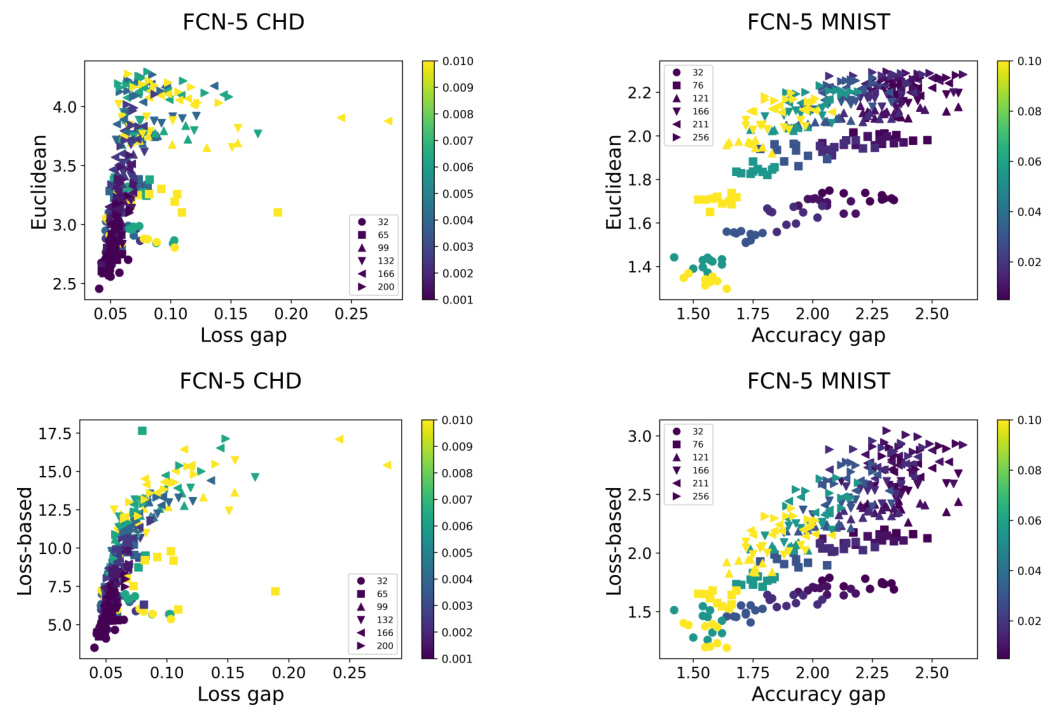
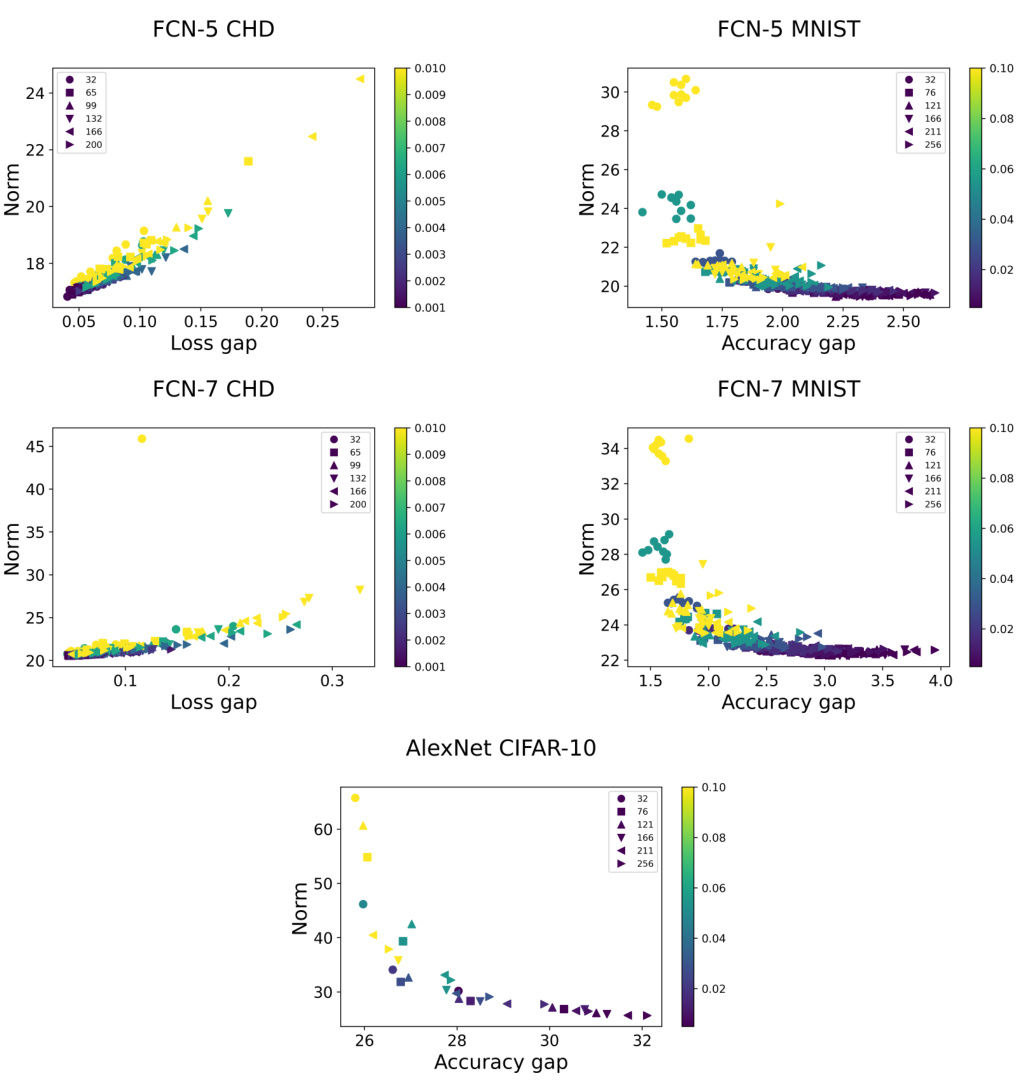
This table presents the correlation coefficients between different fractal dimension measures (Euclidean and loss-based) and generalization gap. Spearman’s rank correlation coefficient (ρ), the mean granulated Kendall rank correlation coefficient (Ψ), and the standard Kendall rank correlation coefficient (τ) are reported. The table also includes correlations with the L2 norm of the final parameter vector and the learning rate/batch size ratio. Results are shown for different datasets and network architectures. The standard deviation is reported for CHD and MNIST datasets, indicating the results are averaged across 10 different random seeds for those datasets. AlexNet CIFAR-10 results are based on a single seed.
In-depth insights#
Fractal Limits#
The concept of “Fractal Limits” in the context of a research paper likely explores the boundaries and constraints of using fractal geometry to model complex systems. It could delve into situations where the fractal approach breaks down, highlighting limitations in its predictive power or explanatory capabilities. This might involve examining scenarios where the assumptions underlying fractal models are violated, such as the presence of non-self-similar structures or deviations from scale invariance. The analysis could also investigate the computational complexity associated with fractal analysis of high-dimensional data, thus emphasizing the practical challenges of applying fractal methods in certain contexts. Furthermore, it might compare the fractal approach against alternative modeling techniques to evaluate its relative strengths and weaknesses, perhaps demonstrating that fractal methods are not always superior for representing all types of phenomena. The discussion might conclude by suggesting potential areas for future research to enhance the applicability and robustness of fractal models, or to propose entirely different approaches for modeling systems that are unsuitable for fractal analysis.
Adversarial Fails#
The concept of “Adversarial Fails” in the context of evaluating fractal dimension as a measure of generalization in neural networks is a critical finding. It highlights a failure mode where models initialized adversarially, designed to perform poorly, surprisingly show higher fractal dimension measures than models with poor generalization from random initialization. This contradicts the expected correlation between high fractal dimension and poor generalization, implying that fractal dimension alone is insufficient to capture the complexities of generalization. This result underscores the need for more robust and comprehensive measures that account for various initialization strategies and optimization dynamics, instead of solely relying on topological properties. The study suggests that while topological features may offer some insights into the generalization process, they cannot fully explain or predict generalization performance in all circumstances. Further research should delve into the causal relationships between topological data analysis, optimization trajectories, and generalization ability, exploring more advanced topological methods to find stronger correlations.
PH Dimension#
The study explores persistent homology (PH) dimension as a novel measure for assessing the generalization ability of neural networks. PH dimension, a concept rooted in topological data analysis, quantifies the complexity of the optimization trajectory in the model’s parameter space. The authors investigate the correlation between PH dimension and generalization performance, finding mixed results. While some experiments show a positive correlation, suggesting that models with lower PH dimension generalize better, other scenarios reveal confounding factors such as hyperparameter settings and adversarial initialization that significantly impact the relationship, highlighting the limitations of PH dimension as a standalone generalization predictor. The study’s findings underscore the need for further investigation into the complex interplay between topological features and generalization in neural networks. Furthermore, the work suggests that other, potentially more robust, topological measures may be more appropriate for characterizing generalization behavior.
Double Descent#
The concept of “double descent” in deep learning is a fascinating phenomenon where model performance initially improves with increasing model size, then degrades, and finally improves again. This counterintuitive behavior challenges traditional learning theory, which suggests that overparameterized models will generalize poorly. The paper investigates the relationship between topological measures, specifically persistent homology dimension, and the double descent phenomenon. It explores whether topological properties of the optimization trajectory can predict generalization behavior across various model sizes and how the two seemingly unrelated concepts might be connected. The finding that Euclidean persistent homology exhibits double descent behavior while the loss-based variant doesn’t, suggests a complex interplay between model capacity, optimization geometry, and generalization performance. Further research is crucial to fully understand this dynamic and refine our theoretical understanding of generalization in deep learning.
Future Work#
Future research could explore several promising directions. Extending the empirical analysis to a wider range of architectures, datasets, and optimization algorithms beyond those considered is crucial to validate the robustness of the findings. Investigating the causal relationship between fractal geometry, topological data analysis, and neural network optimization is key to understanding generalization better. Exploring alternative fractal dimension measures and their correlation with generalization is needed. Furthermore, research into the impact of hyperparameters and implicit bias from optimization methods on the fractal properties of optimization trajectories would provide valuable insights. Finally, developing novel theoretical frameworks that relax stringent assumptions required for existing generalization bounds would be important.
More visual insights#
More on figures
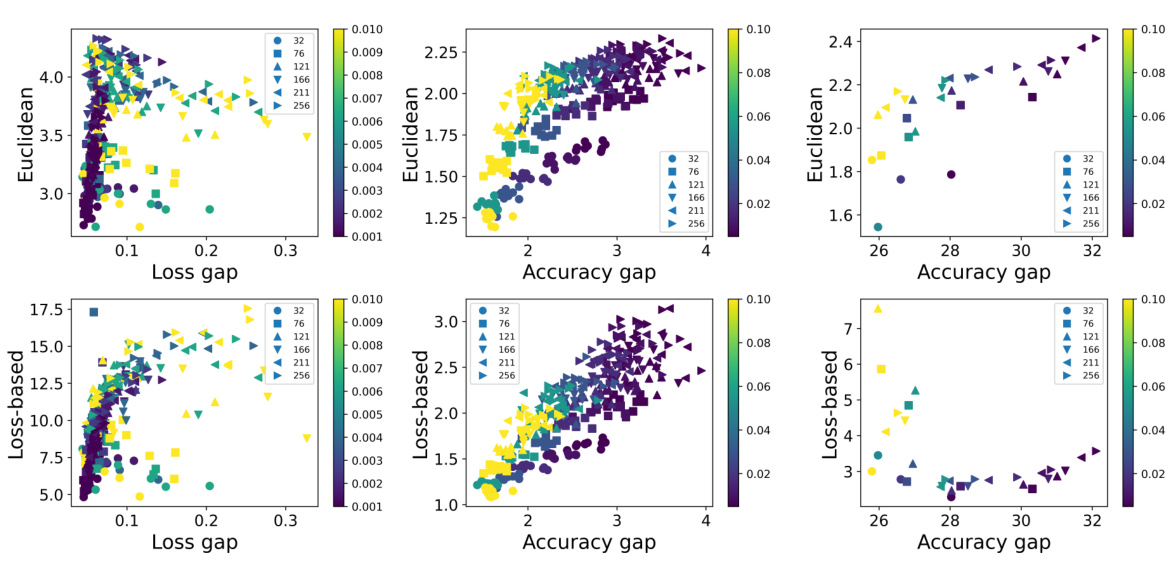
This figure shows the results of an experiment comparing the performance of models trained with adversarial initialization versus random initialization. The x-axis represents the accuracy gap (difference between training and testing accuracy), and the y-axis represents the persistent homology (PH) dimension. The results demonstrate that adversarial initialization leads to a higher accuracy gap, indicating poorer generalization. Furthermore, the PH dimension fails to correctly capture this difference in generalization, highlighting a limitation of using PH dimension as a measure of generalization.
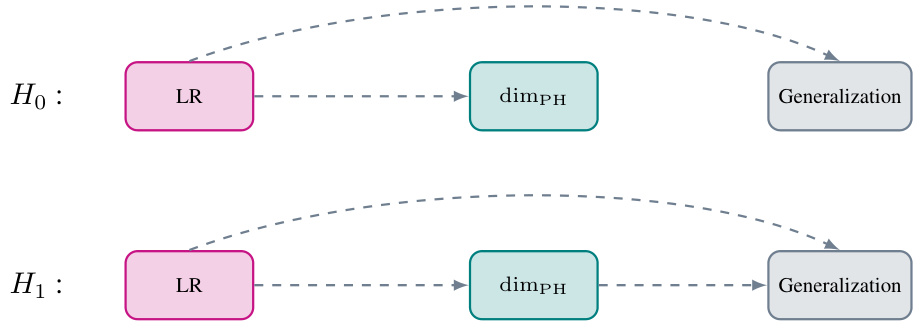
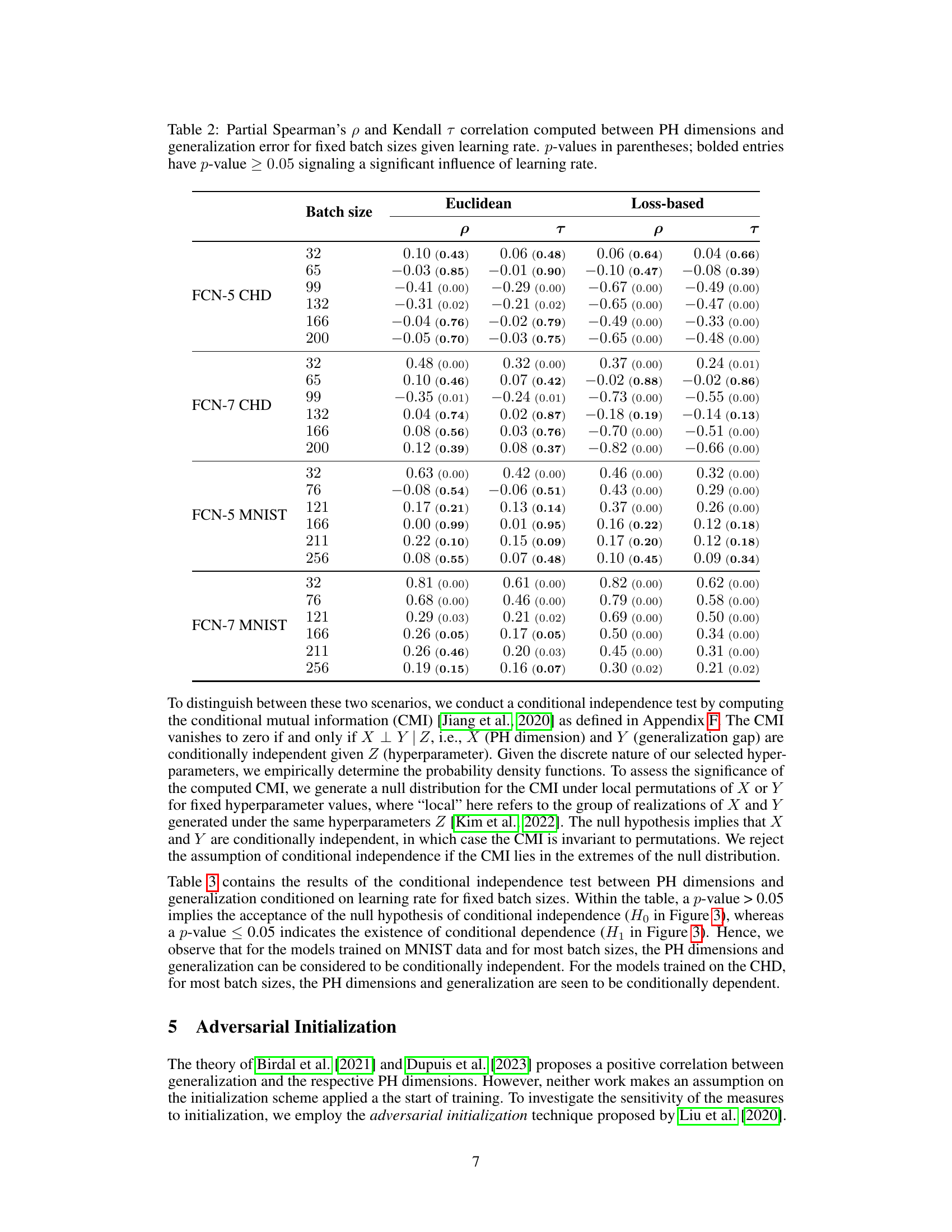
This figure shows two causal diagrams representing two different hypotheses about the relationship between learning rate, PH dimension, and generalization gap. H0 represents the null hypothesis, where learning rate influences PH dimension, but there’s no direct causal link between PH dimension and generalization. H1 is the alternative hypothesis; learning rate influences PH dimension, which in turn directly influences the generalization gap. This figure helps visually explain the conditional independence test used in the paper to determine which hypothesis better fits the data.
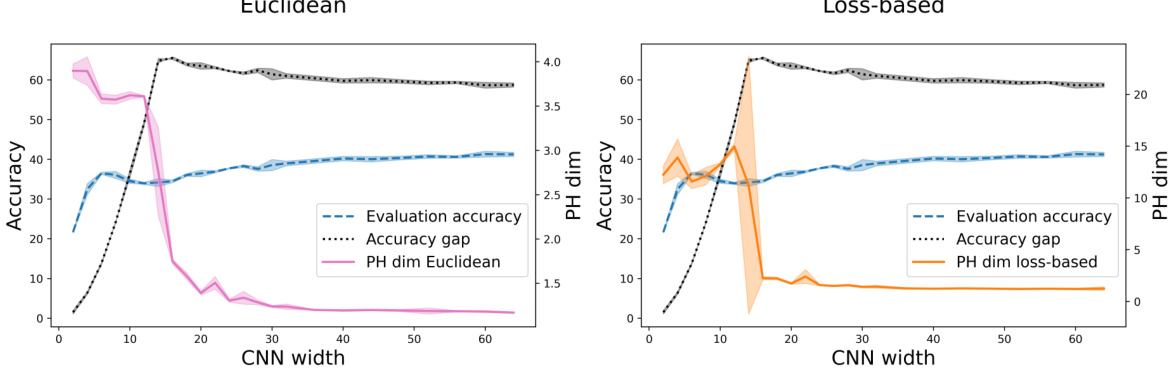
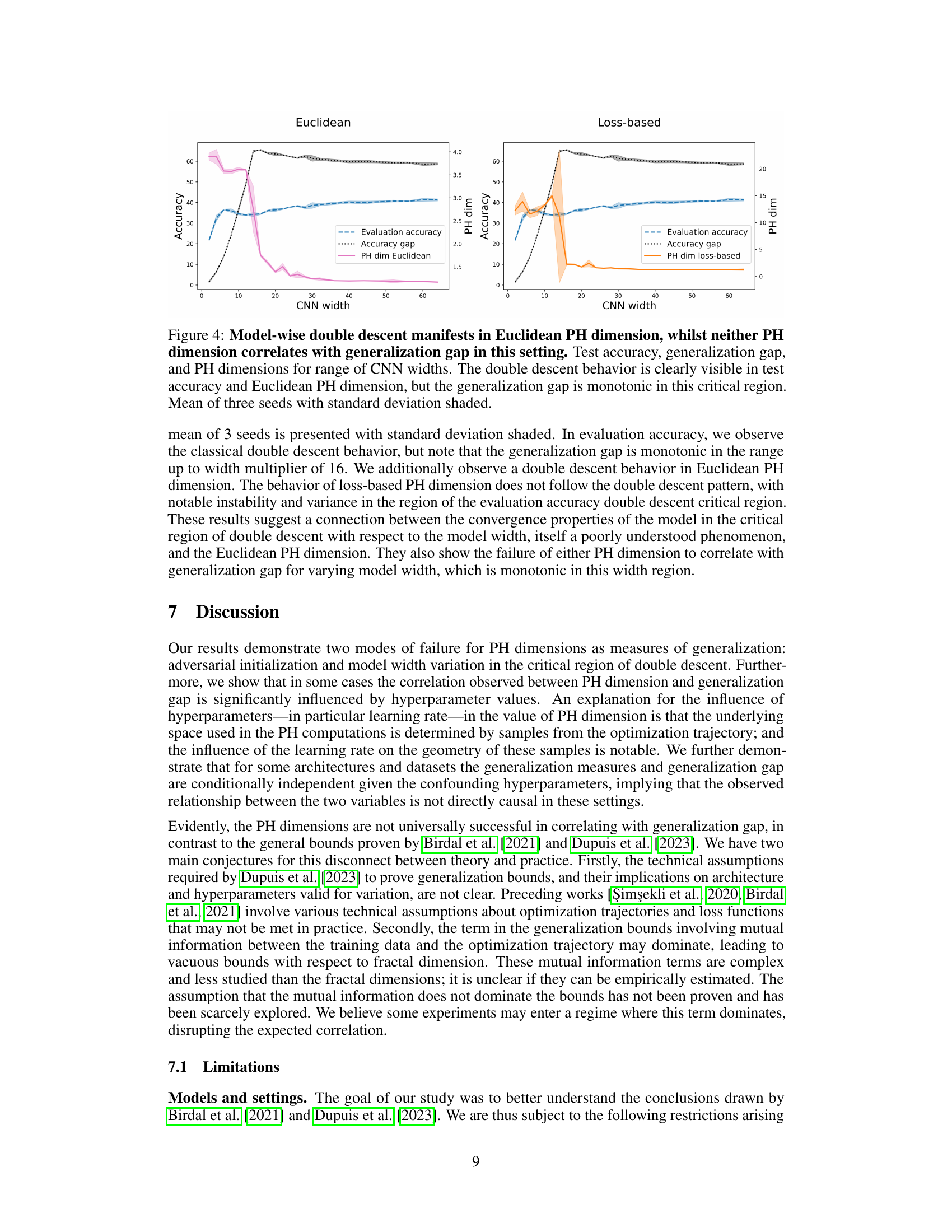
This figure displays the results of an experiment on model-wise double descent using a CNN trained on CIFAR-100 with varying widths. The top panel shows the test accuracy, the middle panel shows the generalization gap, and the bottom panel shows the PH dimensions (Euclidean and loss-based). The key observation is the double descent behavior in test accuracy and Euclidean PH dimension, while the generalization gap remains monotonic. Loss-based PH dimension shows less clear correlation with the other trends.
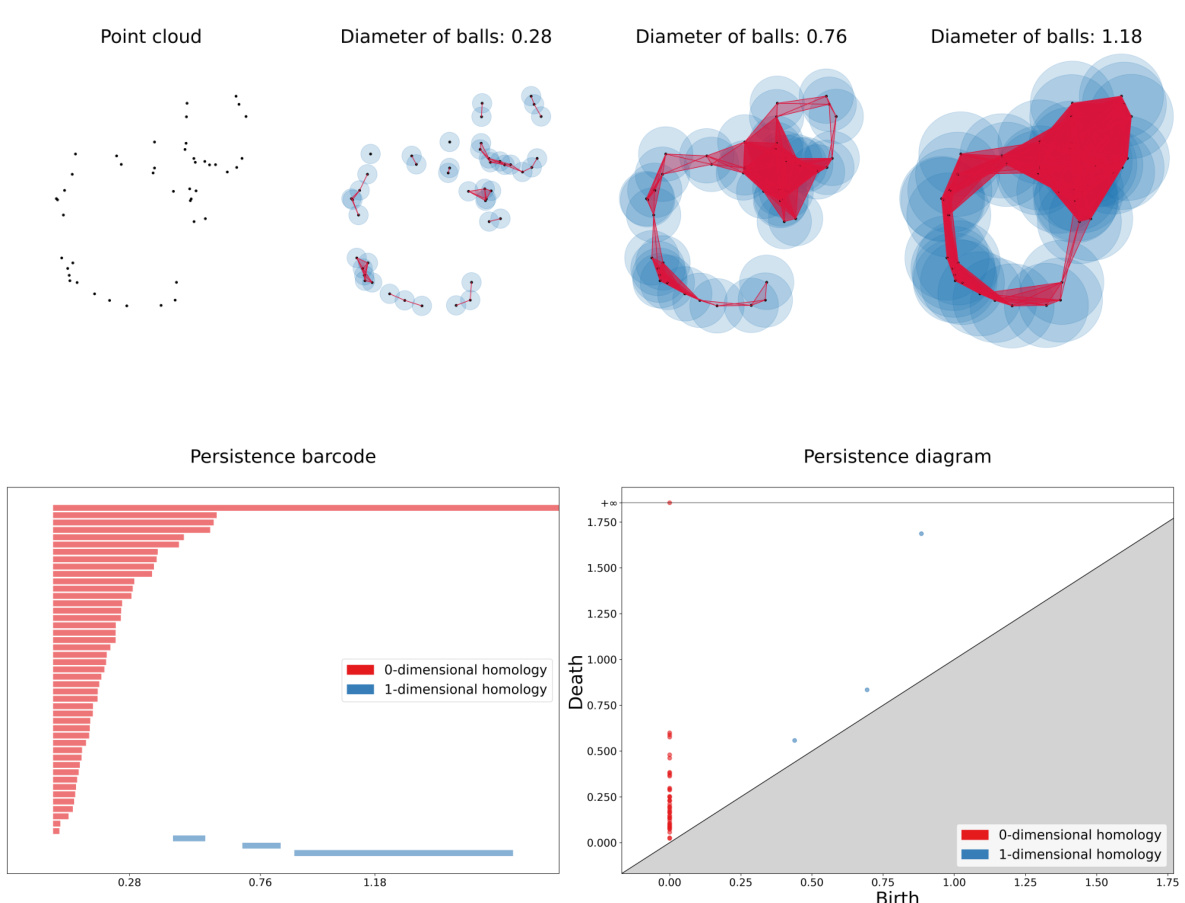
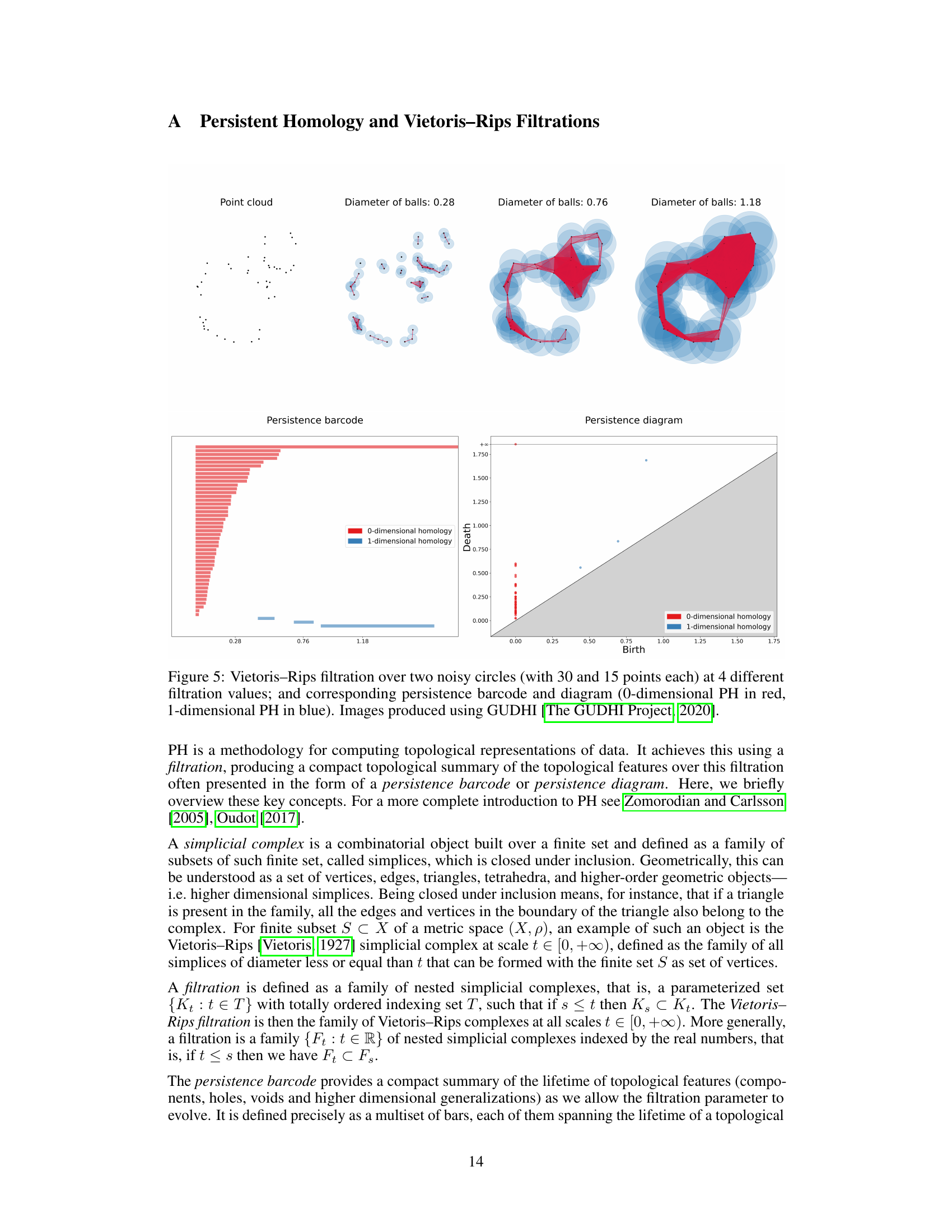
This figure shows an example of Vietoris-Rips filtration applied to a point cloud representing two noisy circles. The filtration is shown at four different scales, progressing from isolated points (0.28) to connected components (0.76) that eventually merge into a single connected component. The corresponding persistence barcode and persistence diagram visualize the topological features (connected components, holes) that emerge and disappear as the filtration progresses, providing a concise summary of the point cloud’s topology. The barcode’s bars represent topological features, and their lengths indicate persistence.
This figure shows the impact of adversarial initialization on the performance of persistent homology (PH) dimension-based generalization measures. It compares models trained with adversarial initialization against models with random initialization across three different network architectures and datasets (FCN-5 MNIST, CNN CIFAR-10, and AlexNet CIFAR-10). The results indicate that adversarial initialization leads to a larger accuracy gap (difference between training and test accuracy), signifying poorer generalization. Importantly, the PH dimensions fail to accurately reflect this poorer generalization; they don’t assign higher PH dimension values to the poorly generalizing adversarial models, contradicting the expected correlation between PH dimension and generalization.
This figure shows the accuracy gap for three different model architectures (FCN-5 MNIST, CNN CIFAR-10, and Alexnet CIFAR-10) trained with both standard (random) and adversarial initializations. The accuracy gap is plotted against the persistent homology (PH) dimension, a measure of the fractal dimension of the model’s optimization trajectory. The results indicate that adversarial initialization leads to larger accuracy gaps compared to random initialization. Importantly, the PH dimension does not consistently reflect the generalization performance, failing to assign higher dimensions to models with larger accuracy gaps when trained with adversarial initialization.
More on tables
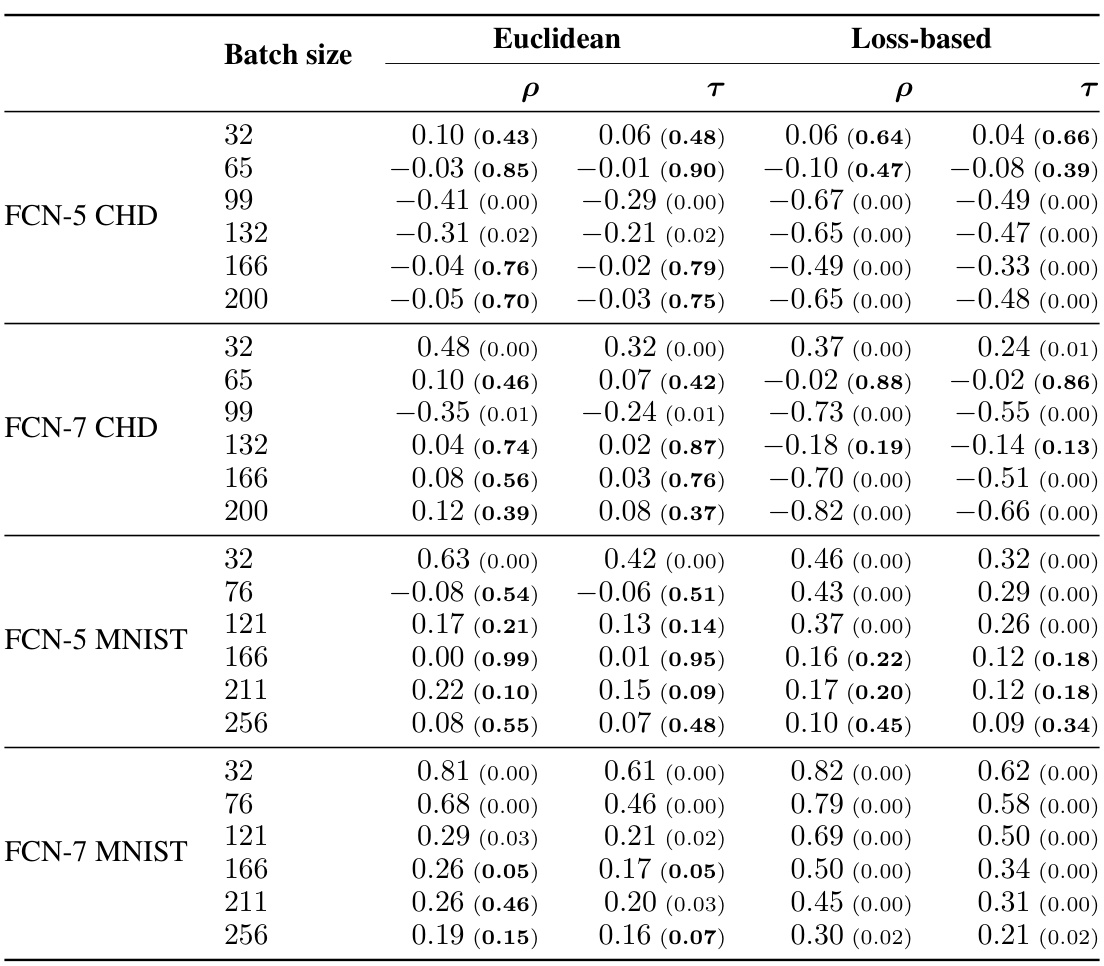
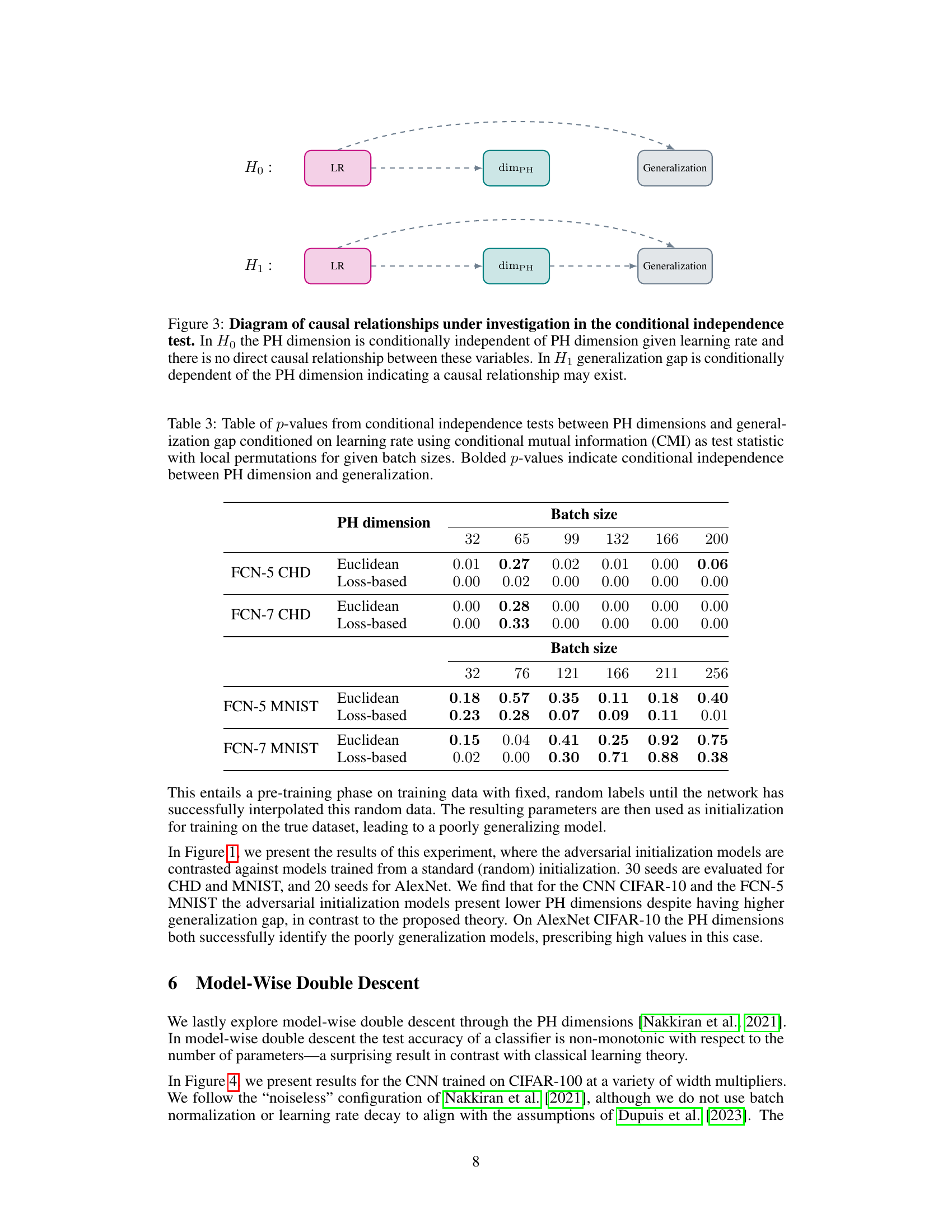
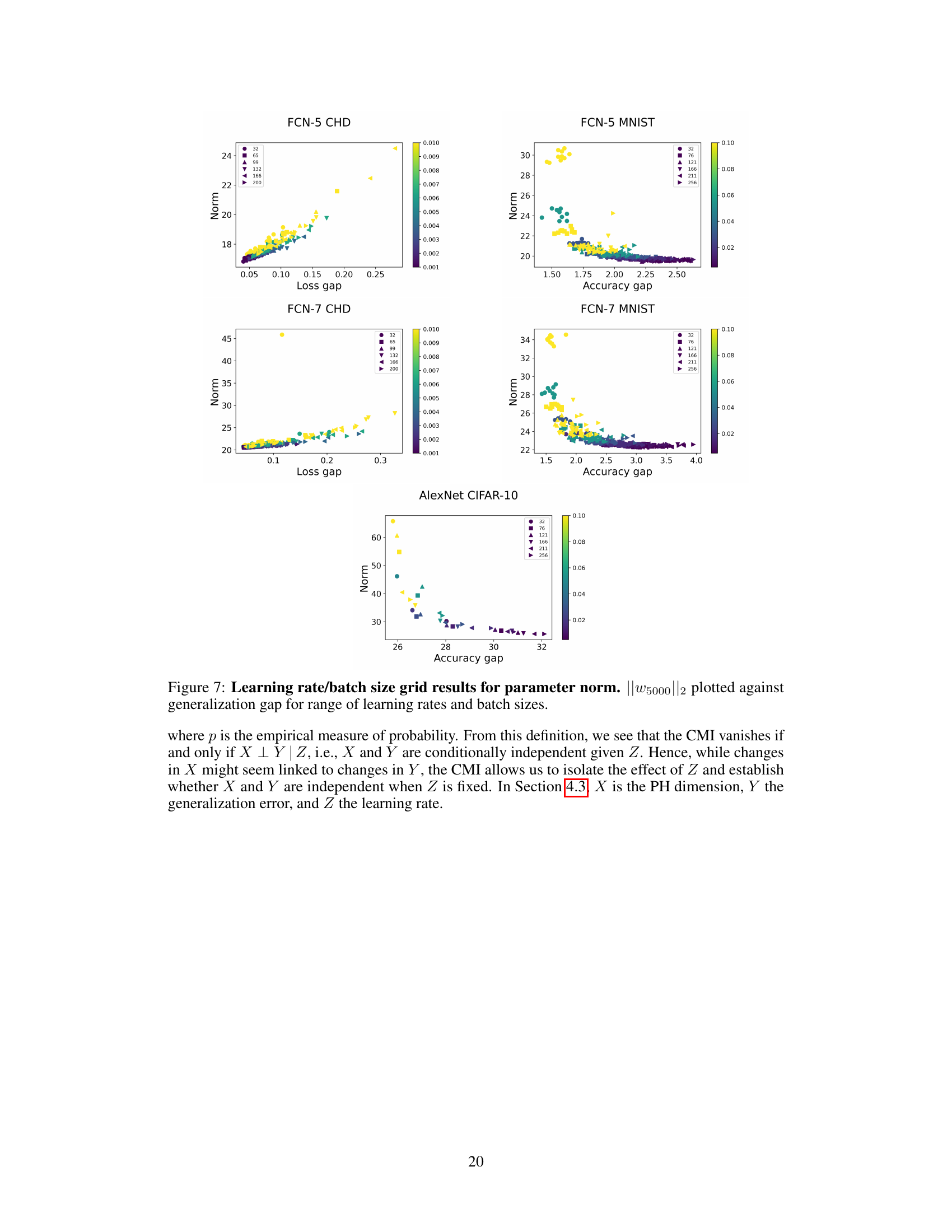
This table presents the results of a partial correlation analysis between persistent homology (PH) dimensions (Euclidean and loss-based) and generalization error, controlling for the effect of learning rate at fixed batch sizes. The table shows the partial Spearman’s ρ and Kendall’s τ correlation coefficients, along with their associated p-values, which indicate the statistical significance of the correlations. A p-value greater than or equal to 0.05 suggests that the correlation between PH dimension and generalization error is not significantly influenced by the learning rate for that specific batch size.
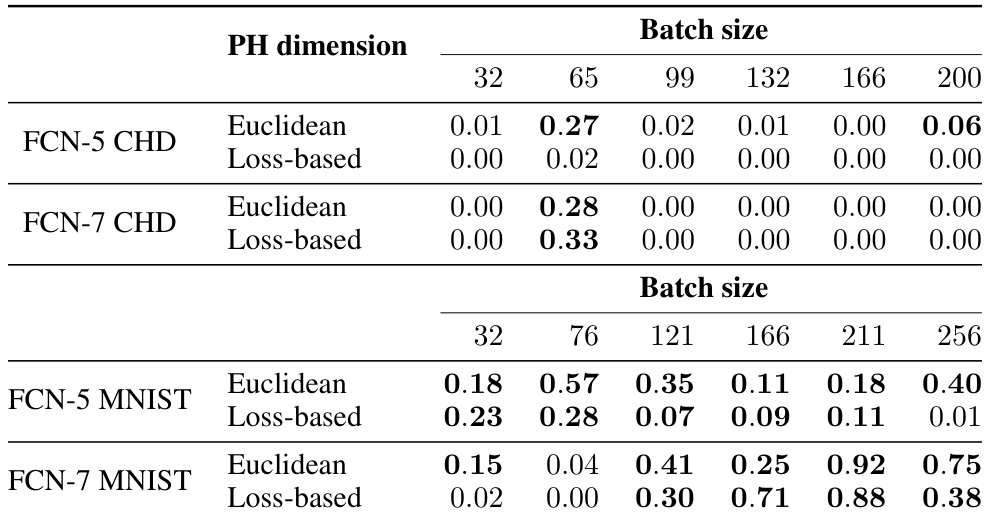
This table presents the partial correlation between PH dimensions (Euclidean and loss-based) and generalization gap, controlling for the effect of learning rate at different fixed batch sizes. The p-values in parentheses indicate the statistical significance of the partial correlation. Bolded values signify that the correlation between PH dimension and generalization gap is not statistically significant, implying a strong influence of learning rate on the observed correlation.
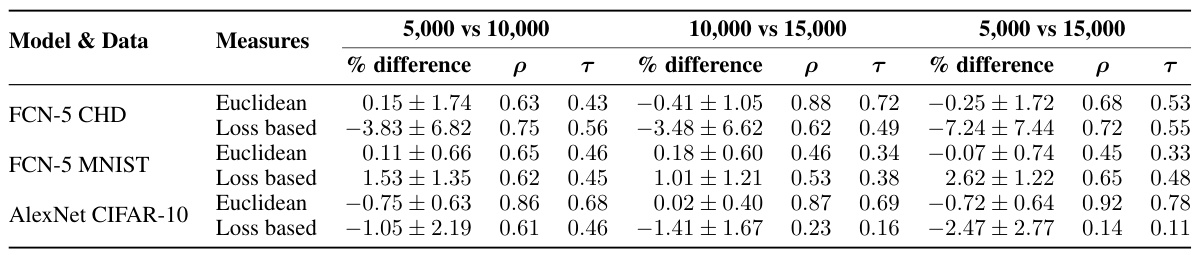
This table presents the correlation coefficients between different fractal dimension measures (Euclidean and loss-based) and the generalization gap. It includes Spearman’s rank correlation coefficient (ρ), the mean granulated Kendall rank correlation coefficient (Ψ), and the standard Kendall rank correlation coefficient (τ). The table also shows correlations with the L2 norm of the final parameter vector and the learning rate/batch size ratio. Results are shown for FCN-5 and FCN-7 models trained on the California Housing Dataset (CHD) and MNIST dataset, as well as AlexNet models trained on CIFAR-10. For CHD and MNIST, the table shows the mean and standard deviation across 10 different random seeds.
Full paper#