AUC Maximization under Positive Distribution Shift

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in imbalanced classification and domain adaptation. It addresses the prevalent issue of positive distribution shift, offering a novel solution that only requires positive labels in the training data, thus overcoming the limitation of existing methods that depend on labeled negative data. The proposed method’s theoretical grounding and strong empirical results open doors for further research into addressing distribution shifts in various real-world applications like medical diagnosis and intrusion detection.

Visual Insights

#

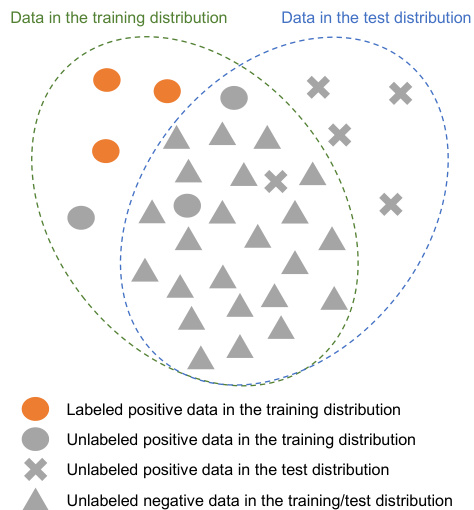
This figure illustrates the data used in the proposed AUC maximization method under positive distribution shift. It shows the different types of data: labeled positive data in the training set, unlabeled positive and negative data in the training set, and unlabeled positive data in the test set. The key assumption is that the negative data distribution remains the same between training and testing, while the positive data distribution may change.

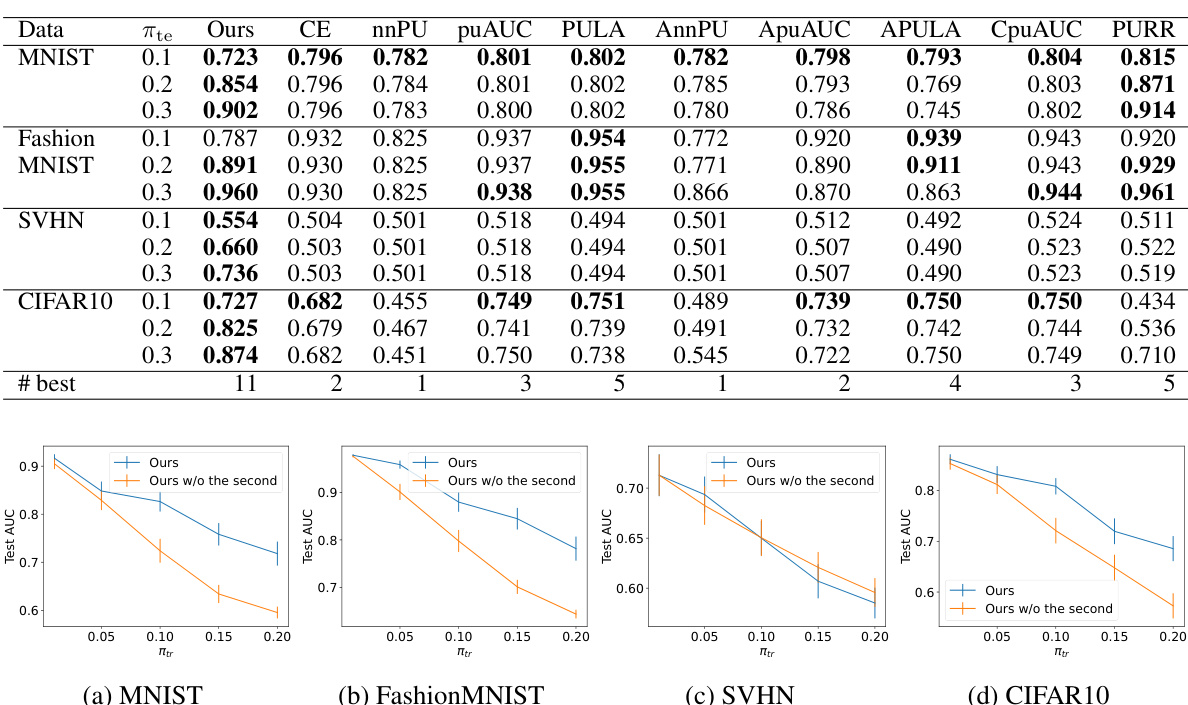
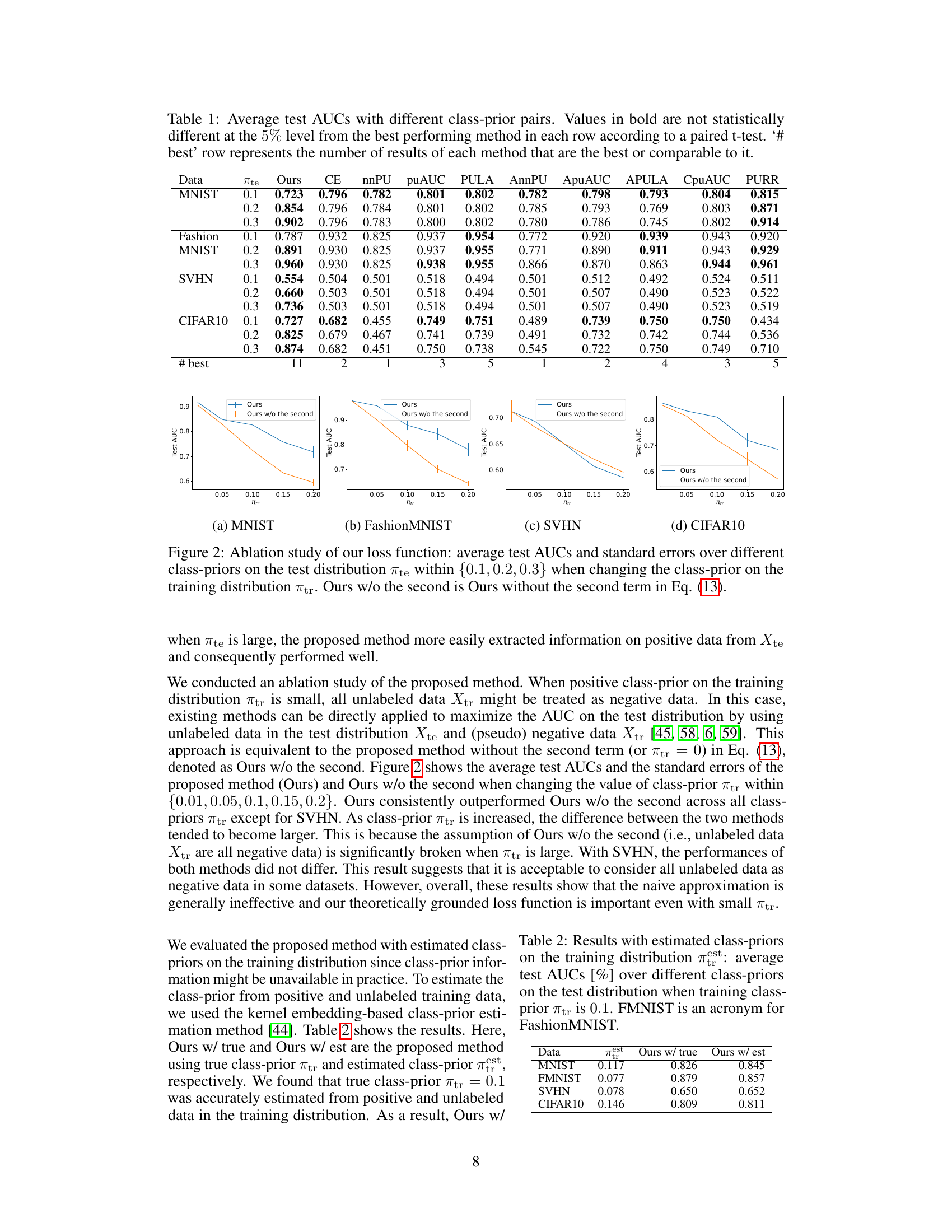
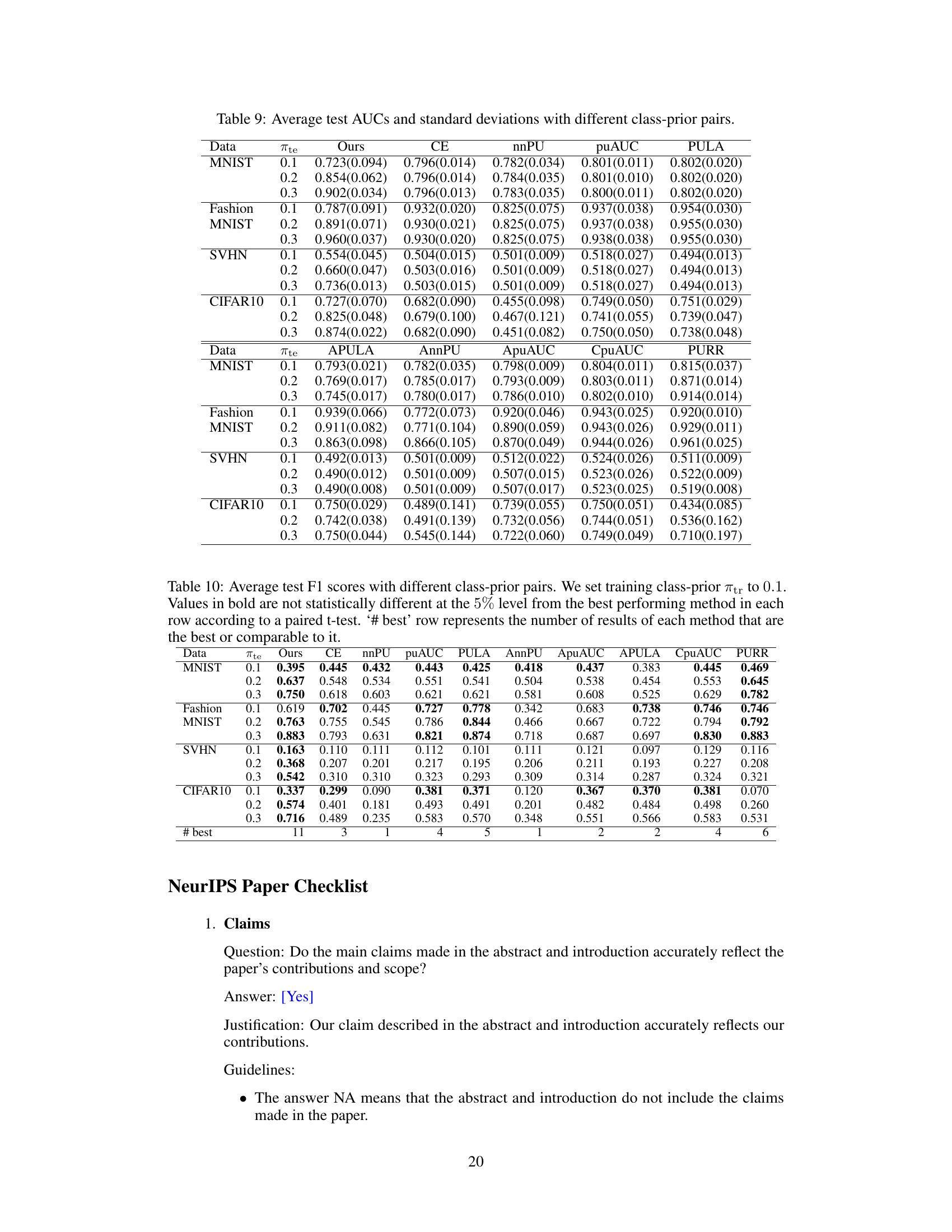
This table presents the average test AUCs achieved by different AUC maximization methods under various class-prior settings on four datasets (MNIST, FashionMNIST, SVHN, CIFAR10). The results are categorized by dataset, the prior probability of the positive class in the test data (πte), and the applied method. Statistical significance is determined using a paired t-test at a 5% significance level. The ‘# best’ row indicates how many times each method performed best or comparably to the best.

In-depth insights

#

AUC Maximization

#

AUC maximization is a crucial task in imbalanced binary classification, aiming to optimize the area under the ROC curve. Traditional methods often assume identical training and test distributions, a condition rarely met in real-world scenarios due to distribution shifts. This paper addresses this limitation by focusing on positive distribution shift, where the negative class density remains constant but the positive class density varies. The core contribution lies in theoretically demonstrating that test AUC can be expressed using training and test distribution densities, allowing the maximization of test AUC using only positively labeled training data and unlabeled data from both training and test sets. This novel approach simplifies implementation and addresses the scarcity of labeled negative data, a common challenge in imbalanced classification. The proposed method’s efficacy is experimentally validated using real-world datasets, highlighting its robustness and practicality in handling distribution shifts.

Positive Shift

#

The concept of “Positive Shift” in machine learning, particularly within the context of imbalanced classification, signifies a scenario where the distribution of positive data changes between the training and testing phases, while the negative data remains consistent. This poses a significant challenge because models trained on the initial positive distribution may not generalize well to the shifted distribution during testing. Understanding the nature of this shift is crucial for developing robust algorithms. Factors such as evolving adversarial attacks (intrusion detection), disease progression (medical diagnosis), or diverse product defects (visual inspection) could contribute to a positive shift. Addressing this challenge often involves techniques that adapt to the new distribution, such as transfer learning or domain adaptation methods. However, these methods frequently require labeled data from the test distribution, which may not always be feasible. The core issue lies in the divergence between training and testing positive data distributions. This calls for techniques that leverage unlabeled data from both distributions effectively to bridge the gap and improve generalization. Developing effective strategies requires careful consideration of the underlying data characteristics and the nature of the shift itself.

Test AUC

#

The concept of ‘Test AUC’ in a machine learning research paper centers on evaluating a model’s performance on unseen data. It measures the area under the Receiver Operating Characteristic (ROC) curve, calculated using the model’s predictions and true labels from a held-out test set. A higher Test AUC indicates superior discrimination ability, meaning the model can effectively distinguish between the positive and negative classes, even on data it hasn’t encountered before. This metric is crucial because it directly assesses generalization, a key goal in machine learning. Unlike training AUC, which might be inflated due to overfitting, Test AUC provides a more reliable estimate of the model’s real-world performance. Analyzing Test AUC is essential for comparing different models and assessing the impact of factors like hyperparameter tuning or dataset biases. A significant difference between training and test AUC may signal overfitting or the presence of a distribution shift, necessitating further investigation. Therefore, the Test AUC is a pivotal evaluation metric that informs model selection and deployment decisions. It helps quantify how well a model truly generalizes, providing valuable insights into model robustness and effectiveness.

Loss Corrections

#

The section on ‘Loss Corrections’ in this research paper addresses a crucial challenge in Positive-Unlabeled (PU) learning, specifically within the context of AUC maximization. The authors acknowledge that standard loss functions might yield negative values, which is problematic. They highlight the ineffectiveness of the commonly used non-negative loss correction in their AUC maximization framework because zero is not a tight enough lower bound for their loss function. This is a significant observation, showing the limitations of directly applying techniques from standard PU learning. The paper proceeds to explore alternative approaches to address this limitation, proposing a modified loss function that incorporates a tighter lower bound derived using the class-prior in the test distribution. This proposed adjustment demonstrates a deeper understanding of the nuances of AUC optimization within the PU learning paradigm and suggests a more robust and effective method for handling imbalanced datasets. The inclusion of this loss correction section speaks to the paper’s rigorousness, carefully considering practical implementation details and theoretical subtleties to improve the overall methodology.

Real-World Data

#

The use of real-world data presents both exciting opportunities and significant challenges. On one hand, real-world data offers a level of realism and diversity unmatched by controlled experimental settings, allowing for the discovery of unexpected patterns and relationships. However, this same complexity can make analysis difficult. Data quality can be inconsistent, with missing values, errors, and biases that must be carefully addressed. Additionally, the heterogeneity of real-world data can make it hard to apply standard statistical techniques, often requiring advanced methods capable of handling high dimensionality, non-linearity, and potentially confounding factors. Finally, ethical concerns related to privacy, bias, and informed consent need careful consideration when working with this data type. Therefore, a rigorous and thoughtful approach, including careful data cleaning, preprocessing, and robust analysis techniques, is essential for extracting valuable insights from real-world data while mitigating potential risks.

More visual insights

#

More on figures

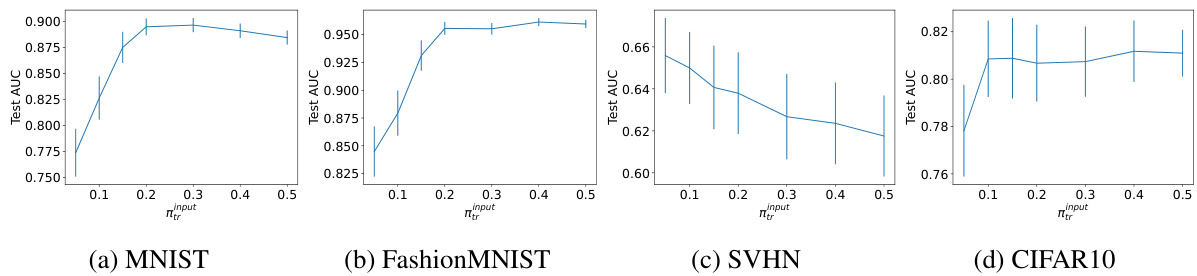
This figure shows the results of an ablation study on the impact of the input class prior (πtr) on the test AUC of the proposed method. The study was conducted across four datasets (MNIST, FashionMNIST, SVHN, CIFAR10) and with three different test class priors (πte). The x-axis represents different input class priors used in the experiment, while the y-axis represents the test AUC. Error bars indicate standard errors. The results indicate that the performance of the proposed method is influenced by how well the input class prior matches the true class prior.

This figure shows the performance of the proposed method when the input class prior on the training data is different from the true class prior. The x-axis represents the input class prior, and the y-axis represents the average test AUC. Each subplot corresponds to a different dataset (MNIST, FashionMNIST, SVHN, and CIFAR10). Error bars represent standard errors. The results show that the performance of the proposed method is relatively robust to differences between the input and true class priors, especially when the input class prior is larger than the true class prior.

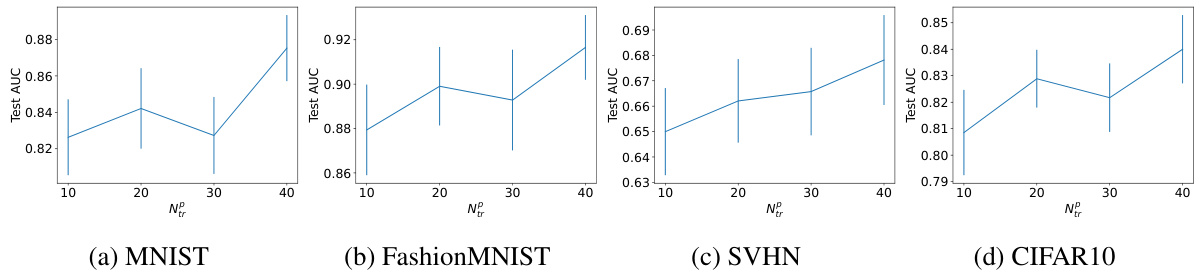
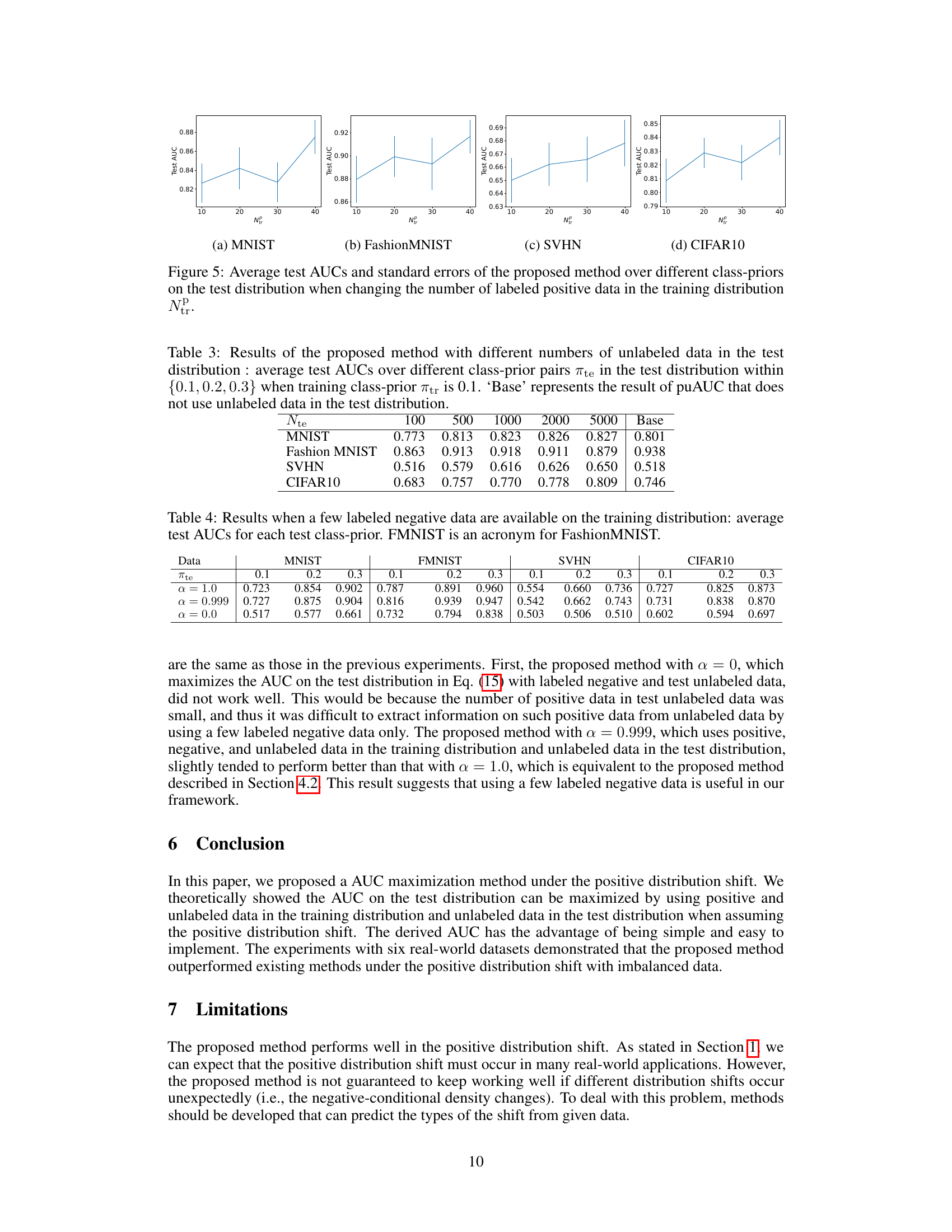
This figure shows how the performance of the proposed method changes when varying the number of labeled positive data (NP) in the training dataset across four different datasets (MNIST, FashionMNIST, SVHN, CIFAR10). Each subplot represents a dataset, illustrating the average test AUC and its standard error. The x-axis represents the number of labeled positive data points in the training set, and the y-axis represents the average test AUC. The error bars indicate the standard deviation, showing the variability of the results. The figure demonstrates the impact of the amount of labeled positive data on the performance of the proposed AUC maximization method.

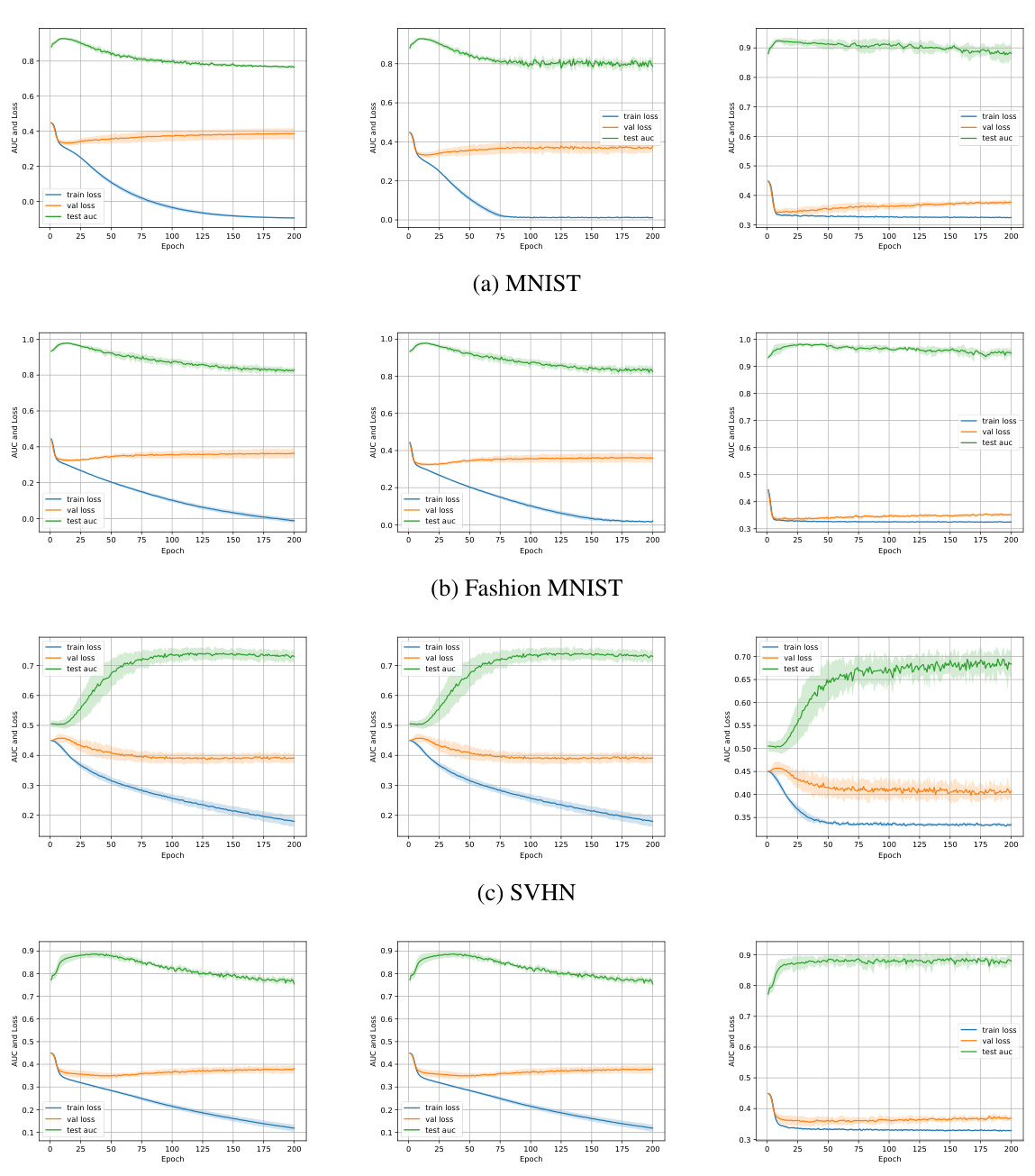
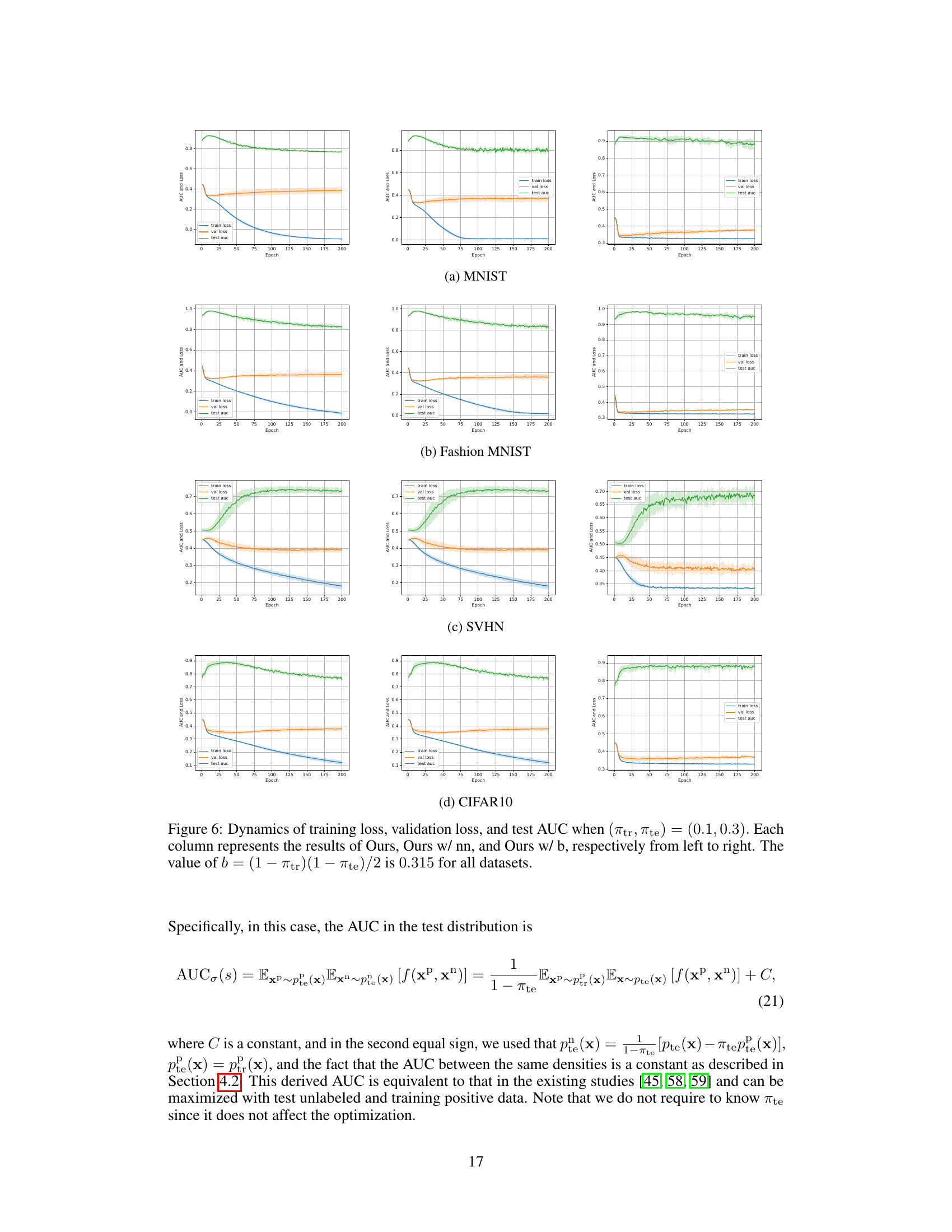
This figure displays the training loss, validation loss, and test AUC over epochs for three variations of the proposed method: the original method, the method with non-negative loss correction, and the method with a tighter loss bound. It shows how these metrics evolve during training for four different datasets (MNIST, Fashion MNIST, SVHN, CIFAR10) and demonstrates the impact of the loss correction techniques on overfitting and model performance. The constant b, used in the tighter bound, is also shown.

More on tables

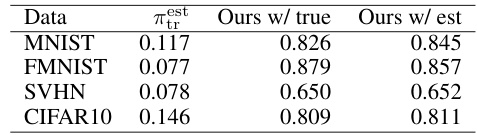
This table compares the performance of the proposed AUC maximization method using true and estimated class priors on the training data. The results show that using the estimated class prior achieves comparable performance to the method using the true class prior. The table includes results for four different datasets: MNIST, FashionMNIST, SVHN, and CIFAR10, each with a different test class prior.

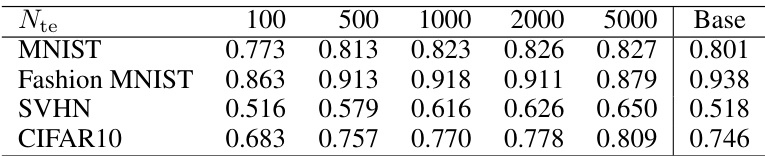
This table shows the average test AUCs of the proposed method with different numbers of unlabeled data in the test distribution. The class-prior in the training distribution is fixed at 0.1, while the class-prior in the test distribution varies across three values (0.1, 0.2, 0.3). The results are compared against a baseline method (puAUC) that does not use any unlabeled data from the test distribution.

This table presents the average test AUCs achieved by different AUC maximization methods under positive distribution shift with four imbalanced datasets (MNIST, FashionMNIST, SVHN, CIFAR10). Each dataset is evaluated under three different class prior scenarios in the test data (0.1, 0.2, and 0.3). The table also indicates the number of times each method produced the best or comparable results across all datasets and scenarios.

This table compares the performance of three variations of the proposed AUC maximization method. The original method (‘Ours’) is compared against versions that incorporate two different loss corrections (‘Ours w/ nn’ and ‘Ours w/ b’). The loss corrections aim to prevent overfitting by addressing potential issues with negative empirical risk estimates. The table shows the average test AUC for each method across different class-prior values (πte) in the test data, while keeping the training class-prior (πtr) constant at 0.1.

This table compares the performance of the proposed method against BPURR, another method designed for positive distribution shift, across four datasets (MNIST, FashionMNIST, SVHN, CIFAR10) at varying test-set class-prior values. The table shows that the proposed method either outperforms or performs comparably to BPURR in most cases, indicating it is a more robust and effective approach for maximizing AUC under positive distribution shift.

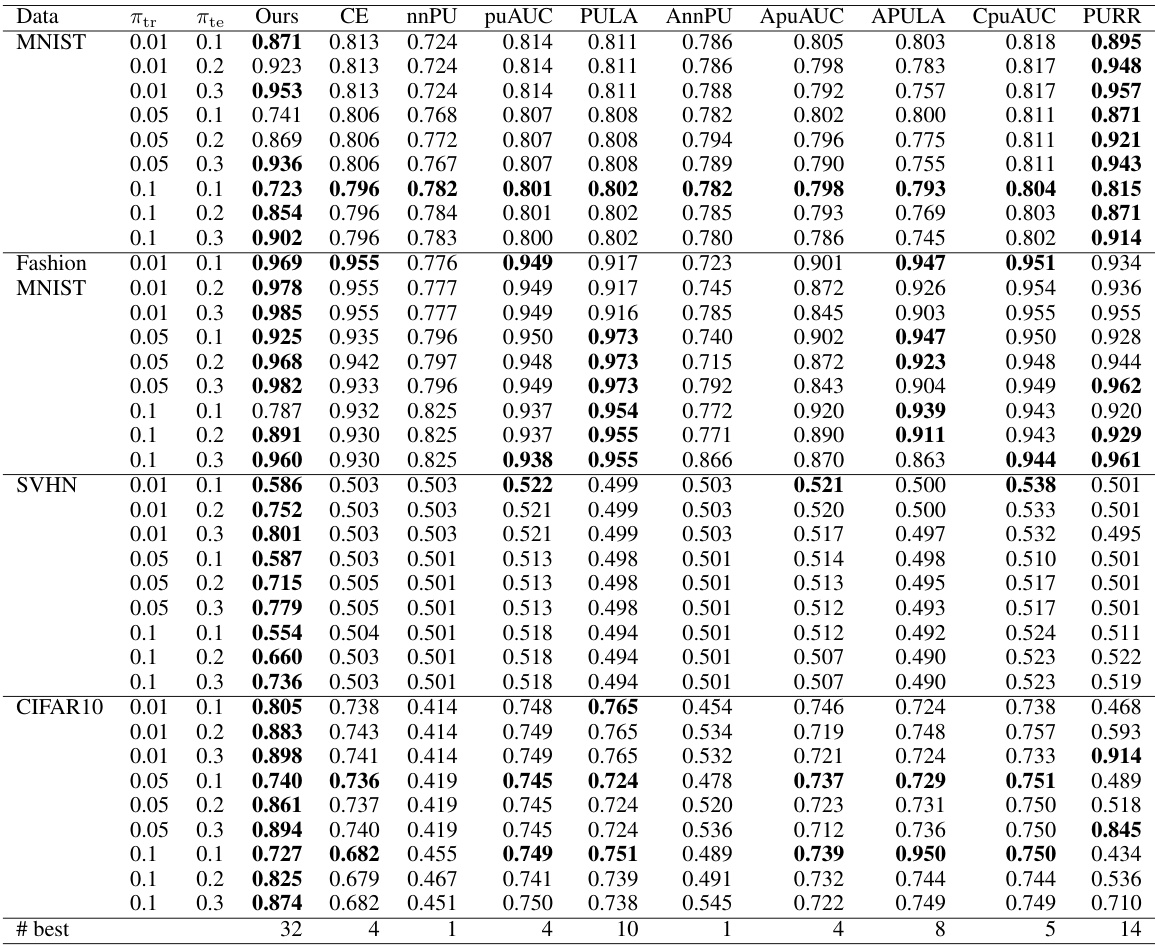
This table presents the average test AUC scores achieved by different AUC maximization methods across four datasets (MNIST, FashionMNIST, SVHN, CIFAR10) under various class-prior settings (πte). The results are compared using a paired t-test to determine statistical significance, indicating which methods perform comparably to the best. The ‘# best’ row summarizes how frequently each method achieved the highest or comparable AUC.

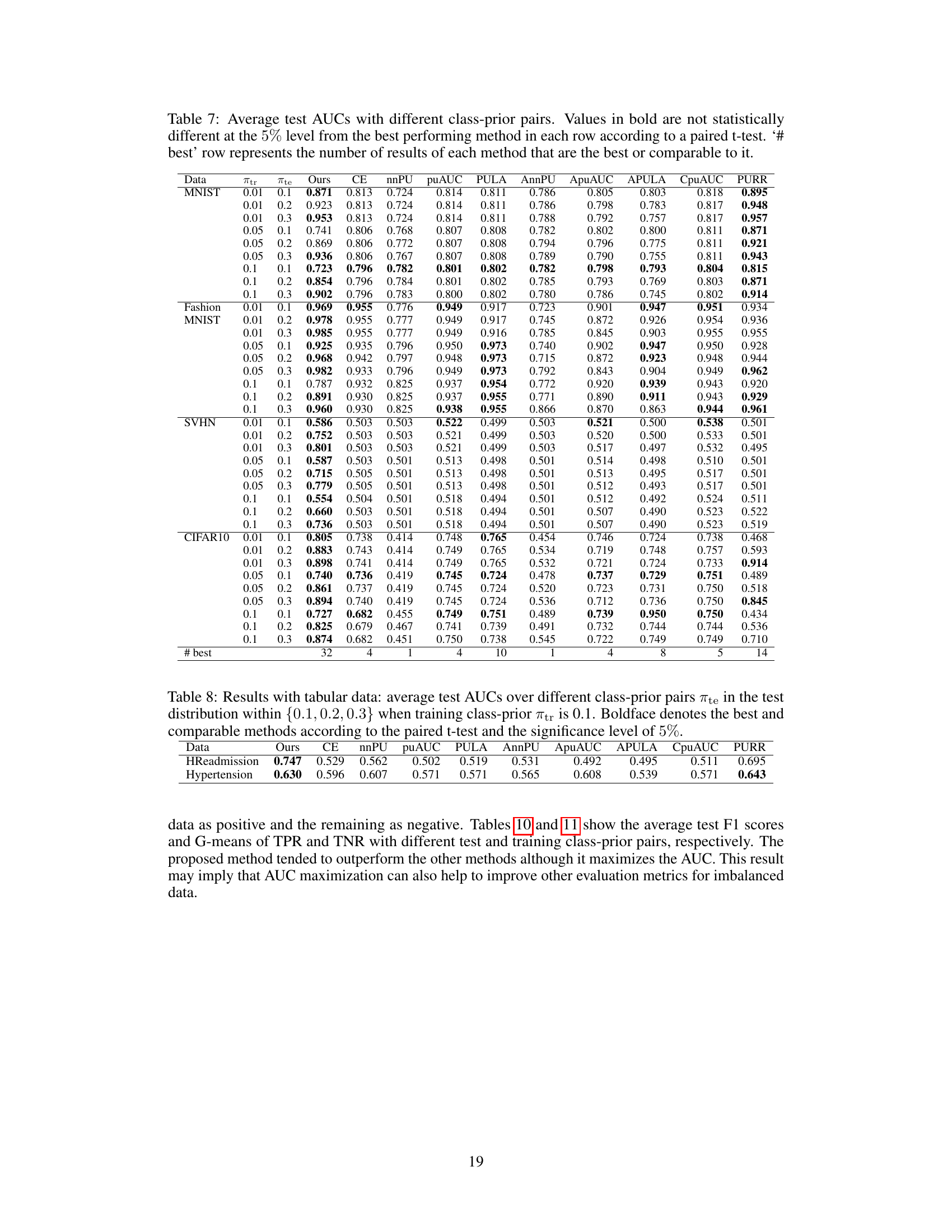
This table presents the average test AUCs achieved by different methods on two tabular datasets, HReadmission and Hypertension, under positive distribution shift scenarios. Each dataset has three different test class-prior values (0.1, 0.2, and 0.3). The table compares the proposed method’s performance against several baselines, highlighting the best-performing method for each scenario using a paired t-test at the 5% significance level.

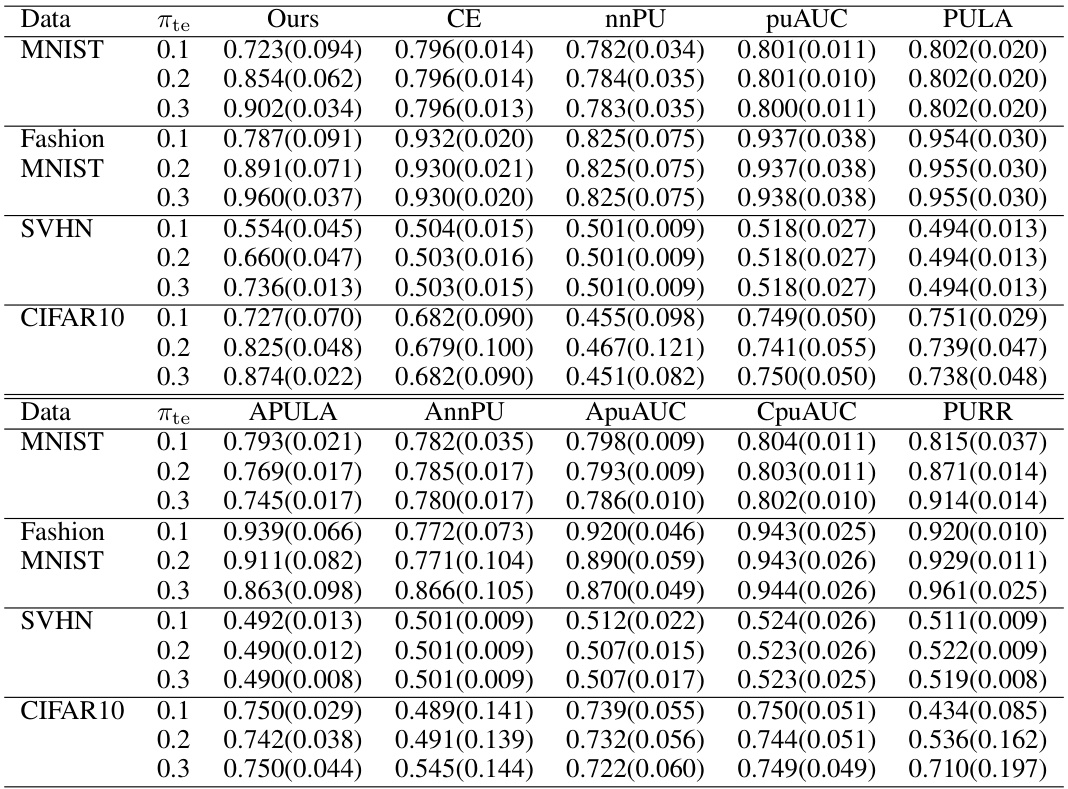
This table presents the average test AUCs achieved by different AUC maximization methods across four datasets (MNIST, Fashion-MNIST, SVHN, CIFAR10) under varying class prior conditions in the test data. The results are compared using a paired t-test to determine statistical significance. The ‘# best’ row summarizes how often each method achieved the highest or comparable AUC across all conditions.

This table presents the average test AUCs achieved by different AUC maximization methods across four datasets (MNIST, FashionMNIST, SVHN, CIFAR10) under varying class-prior conditions in the test data. The results are compared using a paired t-test to determine statistical significance. The ‘# best’ row summarizes how often each method achieved the best or comparable performance.

This table presents the average test AUCs achieved by different AUC maximization methods across four datasets (MNIST, FashionMNIST, SVHN, CIFAR10) under varying class-prior conditions in both training and testing distributions. The results are statistically analyzed using a paired t-test to identify methods that perform comparably to the best-performing method. The ‘# best’ row summarizes the number of times each method achieves the best or comparable performance.

Full paper

#