↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated offline reinforcement learning (RL) presents significant challenges due to the inherent limitations of individual client datasets and the privacy concerns associated with data sharing. Existing techniques struggle with data heterogeneity and the diverse quality of policies learned on these small datasets. Simply combining standard offline RL with standard federated learning approaches proves insufficient for achieving optimal results.
The researchers developed FEDORA, a novel algorithm that effectively addresses these challenges. FEDORA utilizes an ensemble learning approach to distill the collective wisdom of the clients, employing strategies to mitigate issues of data heterogeneity and pessimistic value computation. Through various experiments across simulated environments and real-world robotic tasks, FEDORA demonstrates superior performance compared to baseline methods, showcasing its effectiveness in collaboratively learning a high-quality control policy from distributed offline data.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in federated learning and offline reinforcement learning, addressing a critical challenge in applying RL to real-world scenarios with distributed data. It provides a novel algorithm, FEDORA, and offers valuable insights into handling data heterogeneity and ensemble diversity, opening up new avenues for research in privacy-preserving collaborative RL.
Visual Insights#
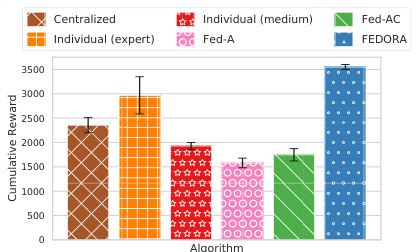
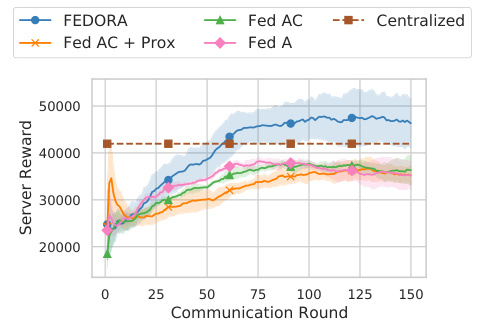
This figure compares the performance of various offline reinforcement learning algorithms on the Hopper environment from MuJoCo. It showcases the results for different approaches including centralized offline RL (trained on combined data from all clients), individual offline RL (trained separately on each client’s data), and three federated offline RL approaches (Fed-A, Fed-AC, and FEDORA). FEDORA is shown to significantly outperform the other federated approaches and performs comparably to centralized training, despite the use of only local data at each client, highlighting its strength in handling heterogeneous data and learning from ensembles of policies.
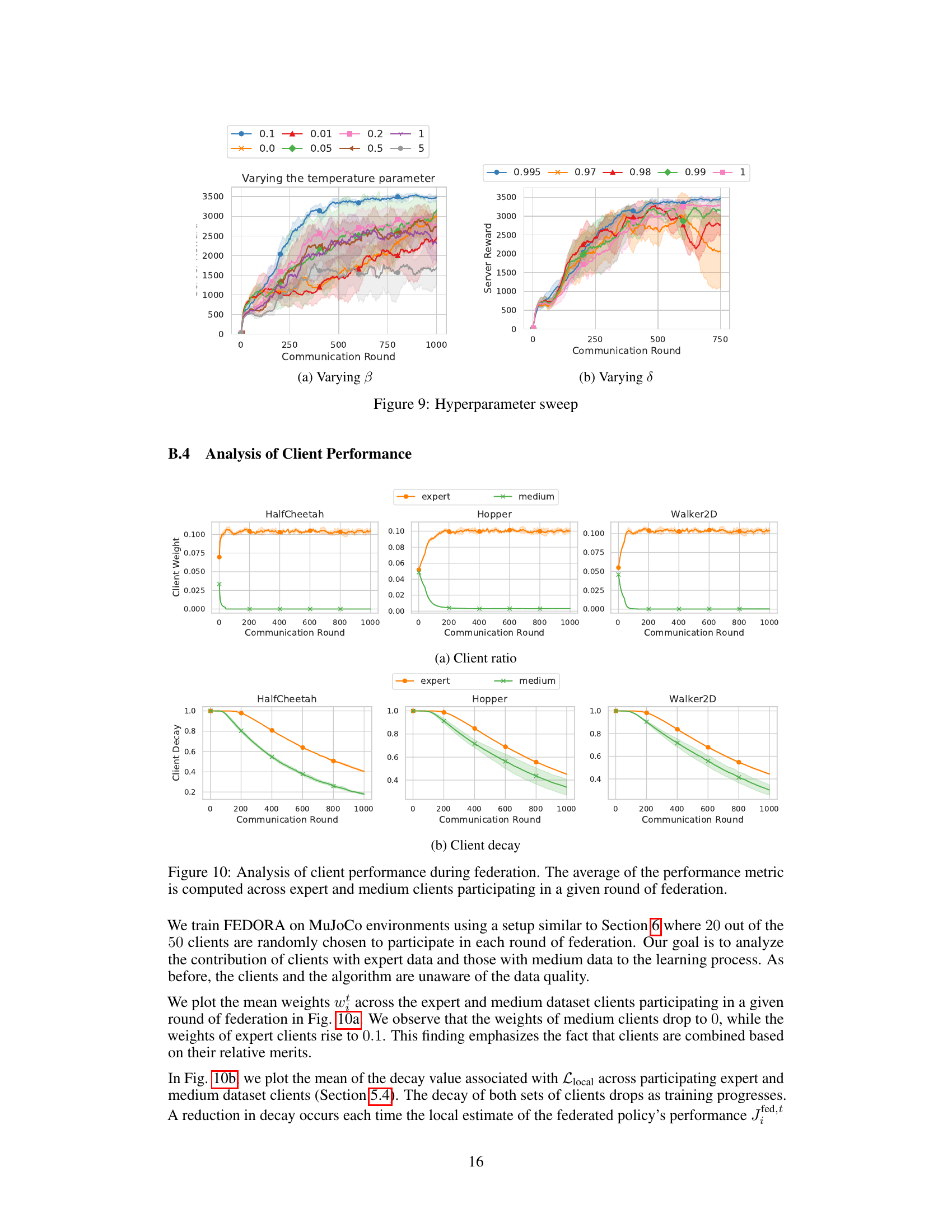
This figure analyzes the performance of clients (with expert and medium quality data) during the federated learning process. It shows how the average performance metric changes over communication rounds, highlighting the contribution of different client data qualities to the overall federated learning process. The plots visualize the performance of clients with expert and medium datasets in various environments (HalfCheetah, Hopper, Walker2d). The analysis covers both client ratios (the proportion of expert and medium clients participating) and client decay (how the influence of local data decreases over time), illustrating the impact of various factors on individual client performance and their overall contribution to the federated model.
In-depth insights#
Fed Offline RL#
Federated offline reinforcement learning (Fed Offline RL) presents a unique challenge in machine learning by combining the complexities of offline RL with the distributed nature of federated learning. The core problem lies in collaboratively training high-quality reinforcement learning policies across multiple clients using only pre-collected, local datasets. Each client’s data is generated under different, unknown behavior policies, leading to significant heterogeneity. Naively applying standard offline RL and federated learning techniques often results in suboptimal performance. Key challenges include handling the ensemble heterogeneity of locally-trained policies, overcoming pessimistic value computation inherent in offline RL, and mitigating data heterogeneity across clients. Successful Fed Offline RL algorithms must address these issues through innovative approaches, such as ensemble learning techniques to distill collective client wisdom and sophisticated regularization methods to ensure policy convergence despite data inconsistencies. The development of robust, efficient Fed Offline RL algorithms has significant implications for real-world applications where centralized data collection is impractical or impossible, while respecting user privacy.
Ensemble Learning#
Ensemble learning, in the context of federated offline reinforcement learning (RL), offers a powerful strategy to overcome the limitations of individual learners trained on heterogeneous data. Instead of relying on a simple average of models, ensemble methods leverage the collective wisdom of multiple policies and critics. This is crucial because individual clients’ data may be of varying quality and relevance due to the diverse behavior policies under which data were collected. By carefully weighing the contributions of different agents, an ensemble approach can identify and emphasize high-performing policies, mitigating the negative influence of poorly trained or biased models. The weighting schemes, often incorporating techniques such as maximum entropy, are designed to encourage diversity and prevent dominance by a few exceptionally good, yet potentially over-specialized, learners. This approach enhances the robustness and overall performance of the final federated policy, addressing the challenges of ensemble heterogeneity that hinder standard federation strategies in offline RL.
Heterogeneous Data#
The concept of “Heterogeneous Data” in federated learning is crucial, especially within the context of offline reinforcement learning. It highlights the challenge of combining datasets collected under different and often unknown behavior policies. This heterogeneity introduces significant complexities because the data from each client may reflect vastly different levels of expertise or operational conditions. Simply averaging models trained on these diverse datasets, as in a naive federated approach, can be severely detrimental, leading to poor performance or even worse results than utilizing individual local data. Therefore, effective strategies, such as FEDORA, must address this issue by leveraging the collective wisdom of the ensemble of policies, not simply averaging their parameters. Regularization techniques are essential to manage distribution shift and mitigate the biases introduced by heterogeneous local training. Methods for assessing the quality of each client’s dataset and assigning weights accordingly are crucial for successful ensemble learning and optimal federated policy generation. In essence, handling heterogeneous data requires a sophisticated and principled approach that goes beyond simplistic averaging, and the success of federated offline RL rests on its effective management.
Optimistic Critic#
The concept of an “Optimistic Critic” in offline reinforcement learning is crucial for addressing the inherent pessimism of standard offline RL algorithms. Standard algorithms often underestimate the value of actions poorly represented in the offline dataset, leading to overly conservative policies. An optimistic critic, in contrast, actively seeks to overestimate action values, encouraging exploration and potentially better performance. This optimism is particularly important in federated settings where datasets are heterogeneous and sparse at individual clients. By combining optimistic local critics with a globally federated critic, the algorithm benefits from both local and global information, leading to more informed and less conservative policies. However, careful design is needed to avoid overly optimistic estimates that might lead to instability. Regularization techniques and strategies to balance optimism with data-driven estimations are critical elements of a successful optimistic critic approach within a federated learning framework.
FEDORA Algorithm#
The FEDORA algorithm tackles the complex problem of federated offline reinforcement learning, where multiple agents collaboratively learn a high-quality policy from pre-collected, heterogeneous datasets without directly sharing data. Its core innovation lies in its ensemble-directed approach, leveraging the diverse strengths of locally-trained policies and critics from different agents. Unlike naive federation methods, FEDORA avoids simple averaging, instead strategically weighting agents’ contributions based on their performance and employing an entropy-regularized optimization to prevent dominance by a few high-performing agents. Furthermore, it addresses data heterogeneity and the inherent pessimism of offline RL through data-aware regularization and a novel federated optimistic critic. Finally, a mechanism to decay the influence of low-quality local data enhances robustness and global optimality. FEDORA demonstrates a superior approach in diverse environments, showcasing the significant advantages of this sophisticated strategy over naive federation techniques or centralized learning on combined datasets.
More visual insights#
More on figures

The figure compares the performance of FEDORA and other federated offline reinforcement learning algorithms across three MuJoCo environments: HalfCheetah, Hopper, and Walker2D. The x-axis represents the communication round, and the y-axis represents the cumulative reward achieved by the federated policy (server policy). The shaded areas represent the standard deviation across multiple runs. It shows that FEDORA consistently outperforms the other algorithms, especially in the later communication rounds. In each environment, FEDORA converges to a higher cumulative reward than other algorithms, indicating its superior performance in learning high-quality policies from heterogeneous offline data in a federated setting.
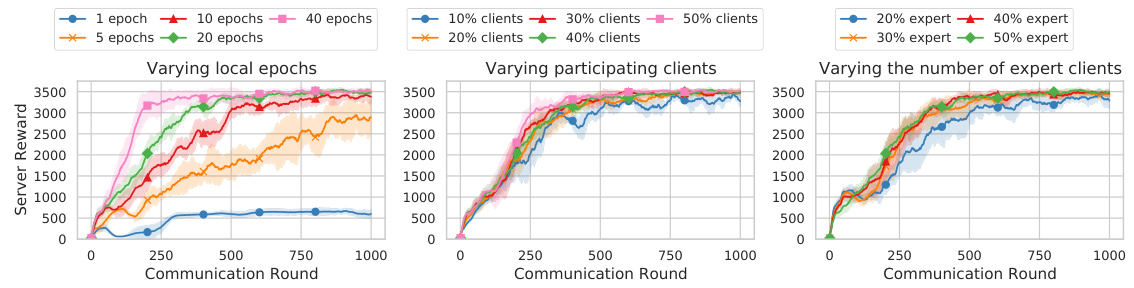
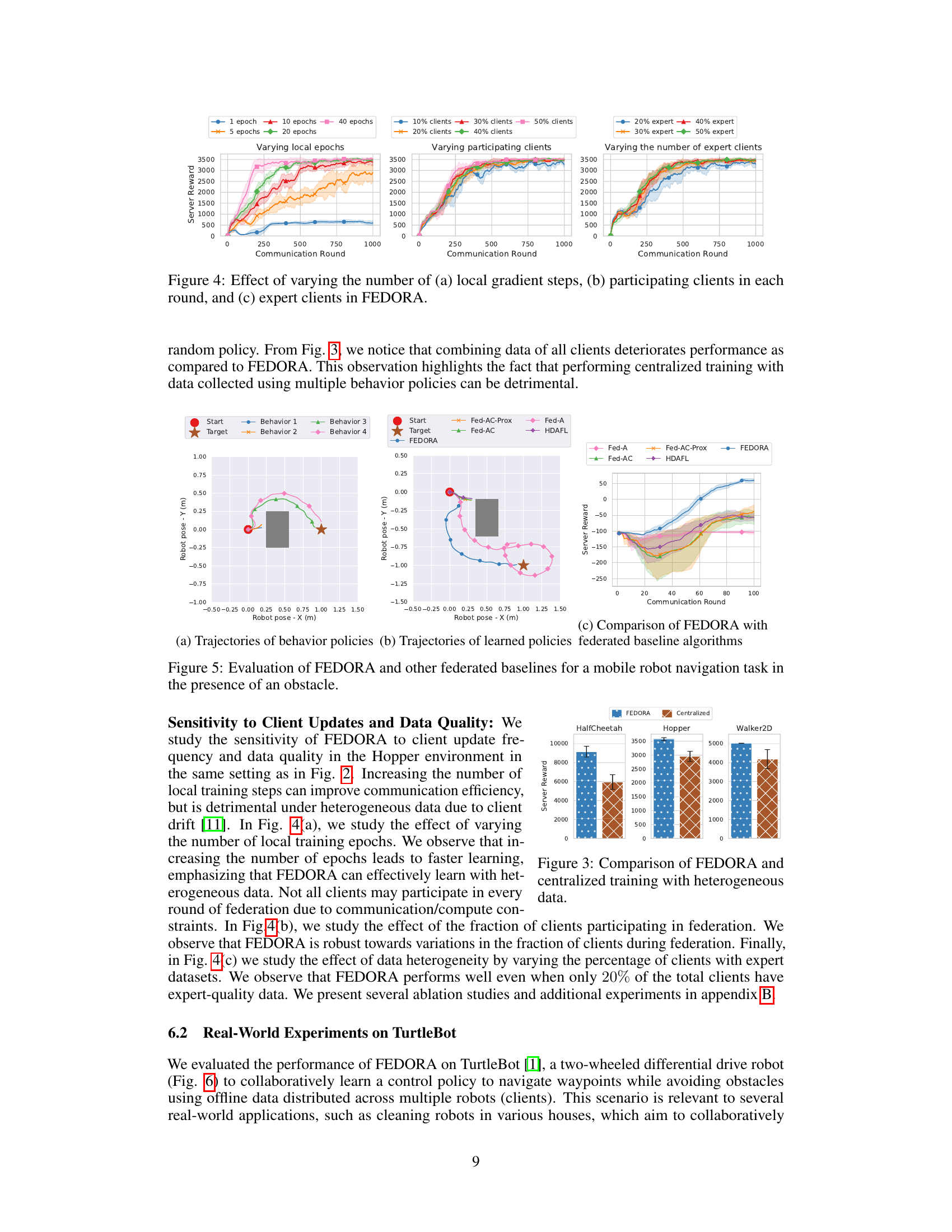
This figure shows the result of an ablation study on FEDORA, investigating the impact of three key factors: the number of local gradient steps performed by each client before model aggregation, the proportion of clients participating in each round of federation, and the percentage of clients possessing high-quality expert data. Each subplot displays the cumulative episodic reward of the server policy across communication rounds, under varying conditions of the parameter in question. The shaded areas represent standard deviation. The results demonstrate FEDORA’s robustness to variations in these parameters, indicating its suitability for real-world applications with diverse client capabilities and data quality.

This figure presents the results of a real-world mobile robot navigation experiment. Subfigures (a) and (b) show the trajectories taken by different behavior policies and the learned policies from various federated offline RL algorithms, respectively. The goal is to navigate to a target location while avoiding an obstacle. (c) shows a comparison of the cumulative rewards achieved by these algorithms over communication rounds. FEDORA demonstrates the ability to successfully navigate to the target while avoiding the obstacle.

The figure shows a comparison of the performance of different offline reinforcement learning algorithms on the Hopper environment from MuJoCo. The algorithms compared are: FEDORA, centralized training, individual training (expert data), individual training (medium data), Fed-A, and Fed-AC. The x-axis represents the algorithm used, and the y-axis represents the cumulative reward. FEDORA outperforms other algorithms, even surpassing centralized training which uses data from all clients. This illustrates the challenges of federated offline RL and the potential benefits of FEDORA’s approach.

This figure shows the TurtleBot3 Burger robot used in the real-world experiments. The robot is a small, two-wheeled differential drive robot equipped with sensors (LIDAR, wheel encoders) and a computer for processing. This platform is used for the real-world validation of the FEDORA algorithm on a mobile robot navigation task.

This figure presents ablation study results to show the impact of each component of FEDORA on the performance. The left subfigure (a) shows the effect of sequentially adding one algorithm component at a time, starting from the naive approach (Fed-A). The right subfigure (b) illustrates the effect of removing individual components from the FEDORA algorithm.
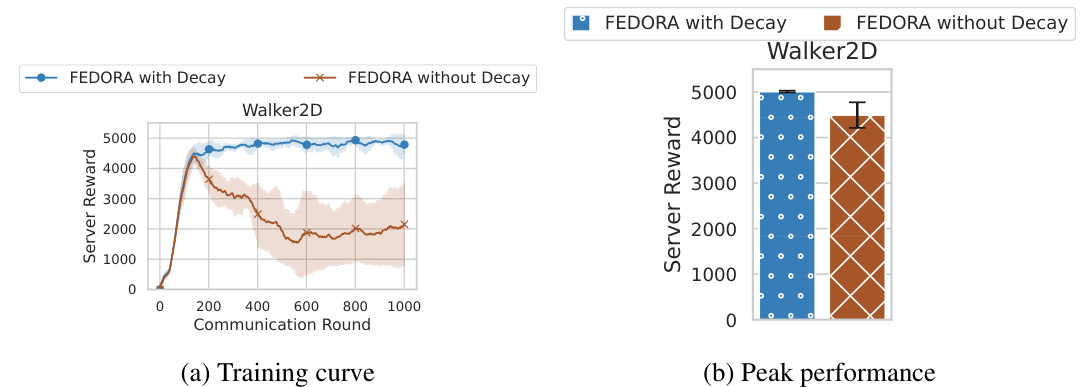
The figure shows the ablation study of the decaying mechanism in the Walker2D environment, comparing FEDORA with decay and without decay. It presents two subfigures: (a) Training curve showing the server reward over communication rounds; (b) Peak performance showing the mean and standard deviation of the peak server reward achieved by each algorithm.

This figure compares the performance of several algorithms on the Hopper environment from MuJoCo. The algorithms include centralized training (combining all data), individual offline RL (training on each client’s data separately), Fed-A (federating only the actor), Fed-AC (federating both actor and critic), and FEDORA (the proposed algorithm). The results show that FEDORA significantly outperforms all the other federated approaches and achieves comparable performance to centralized training, which is a significant advantage considering the distributed nature of federated learning and the privacy advantages it affords.

This figure shows the comparison of cumulative rewards achieved by different offline reinforcement learning algorithms. The algorithms are compared across various scenarios: centralized training (combining all data), individual offline RL (training on individual client data), naive federated offline RL (Fed-A, Fed-AC), and the proposed FEDORA algorithm. The results highlight the challenges of naive federation and the superior performance of FEDORA, which surpasses other approaches, including centralized training on combined data, in terms of cumulative rewards. The plot also visually represents the variability in performance (standard deviation) across different runs.
This figure shows the performance comparison of different federated offline reinforcement learning algorithms and centralized training across various MuJoCo continuous control environments. The x-axis represents the communication round, and the y-axis represents the cumulative episodic reward achieved by the server policy. The plot shows that FEDORA consistently outperforms the other federated approaches (Fed-A, Fed-AC, Fed-AC-Prox, HDAFL) and sometimes even matches or exceeds the centralized training approach.

This figure demonstrates the impact of different hyperparameters on FEDORA’s performance. The subfigures show the cumulative episodic rewards over communication rounds for varying (a) numbers of local gradient steps, (b) percentages of clients participating in each round, and (c) percentages of clients having expert data. The results illustrate FEDORA’s robustness to changes in these hyperparameters.
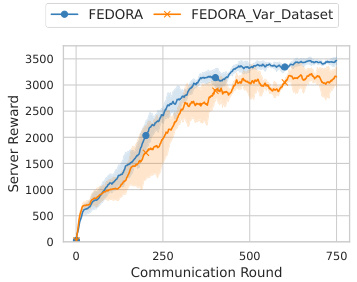
This figure compares the performance of FEDORA with clients having variable dataset sizes against FEDORA with a fixed dataset size. The experiment uses the Hopper-v2 environment with 10 clients (5 with expert data and 5 with medium data). Dataset sizes vary from 4000 to 8000 samples. The results show that FEDORA performs well regardless of variations in dataset sizes, highlighting its robustness and adaptability to heterogeneous data.

The figure shows a performance comparison of different offline reinforcement learning (RL) algorithms in the Hopper environment. It compares centralized training (combining all data), individual offline RL (using only data from a single client), and three federated offline RL approaches (Fed-A, Fed-AC, and FEDORA). The results demonstrate that FEDORA significantly outperforms the other federated methods and achieves comparable performance to the centralized approach, which is generally not feasible in real-world scenarios.
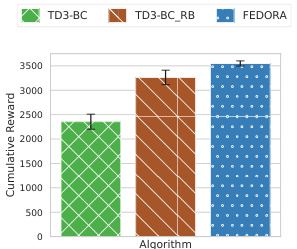
This figure compares the performance of different offline reinforcement learning algorithms in the Hopper environment. The algorithms include centralized training (combining all data from various clients), individual offline RL training on each client’s data, and different federated learning approaches (Fed-A, Fed-AC, FEDORA). FEDORA significantly outperforms the other methods, demonstrating its effectiveness in learning from heterogeneous data.

This figure compares the performance of FEDORA with two other algorithms that use different weighting schemes based on the average reward of the datasets. It shows that FEDORA outperforms both baselines. This is because FEDORA’s weighting scheme combines policies based on their performance, while the other two baselines use average reward, which doesn’t vary much in this setting.
Full paper#