↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current methods for measuring similarity in neural networks using Representational Similarity Matrices (RSMs) are flawed as they couple semantic and spatial information. This coupling leads to inaccurate similarity measures, especially when comparing images with similar content but different spatial arrangements (e.g., translated images). This creates a problem for accurately interpreting how deep neural networks learn and represent data.
This paper proposes semantic RSMs, which are invariant to spatial permutations. The researchers formulate semantic similarity as a set-matching problem and introduce approximation algorithms to improve efficiency. They demonstrate the superiority of semantic RSMs over traditional ones through image retrieval experiments and by comparing their similarity measures to predicted class probabilities. This shows improved accuracy in representing the similarity structure of neural networks, ultimately facilitating a better understanding of their inner workings.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a critical limitation in representational similarity analysis (RSA), a widely used technique for understanding how neural networks represent data. By introducing semantic RSMs, the research offers a new approach to disentangle semantic information from spatial information, which improves the accuracy and reliability of RSA, opening new avenues for understanding neural network representations and their applications.
Visual Insights#
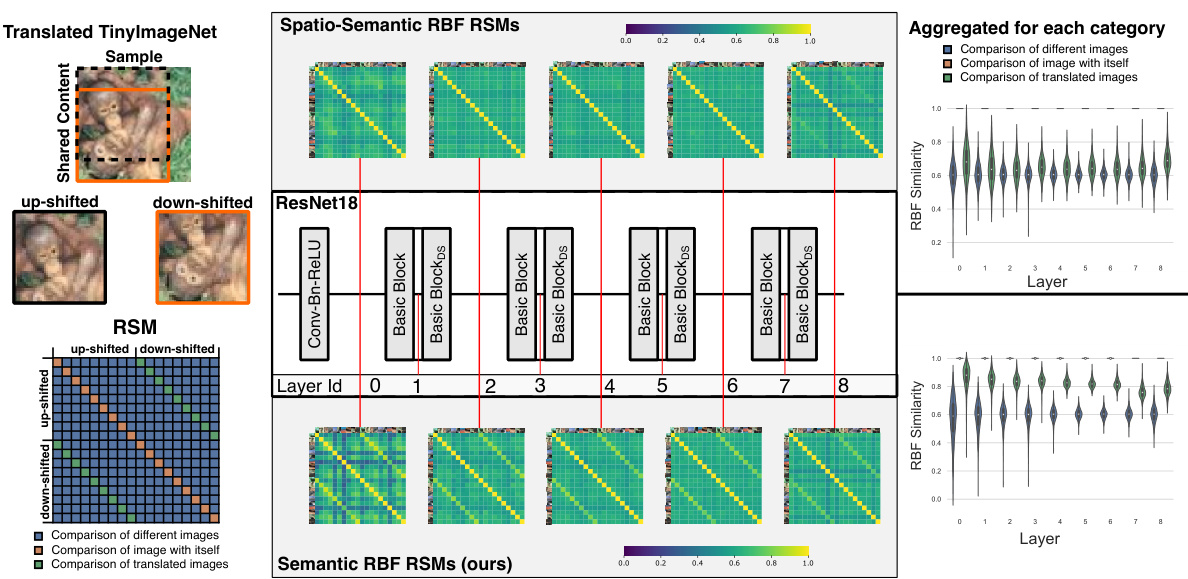
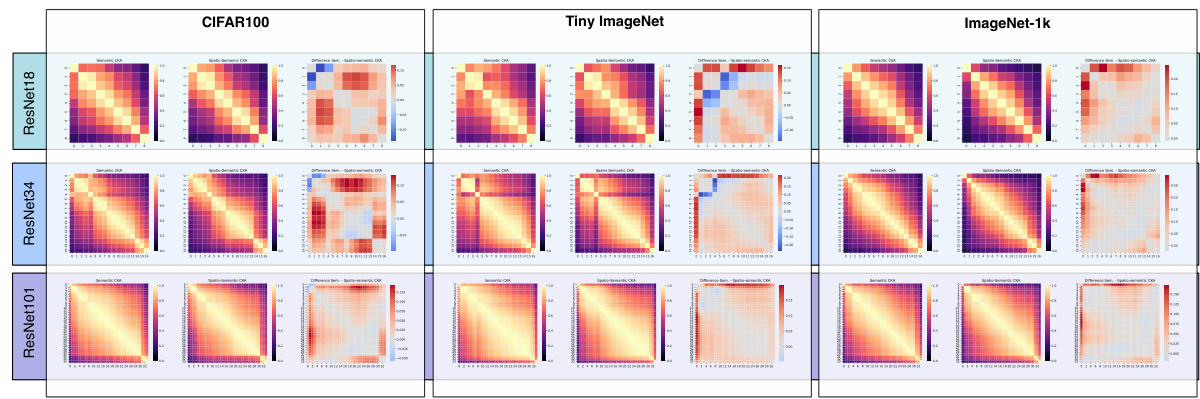
This figure compares spatio-semantic RSMs and semantic RSMs across different layers of a ResNet18 model trained on TinyImageNet. Partially overlapping image crops of the same image are used as input. The top-middle shows the traditional spatio-semantic RSMs, which are sensitive to spatial shifts. The bottom-middle shows the proposed semantic RSMs, which are invariant to spatial permutations. The right side shows the distribution of similarity values for each type of RSM. The results demonstrate that semantic RSMs are better at capturing semantic similarity, even when the images are translated.
This table presents the Pearson correlation between the Jensen-Shannon Divergence (JSD) of predicted class probabilities and the representational similarity (using different kernels: Cosine, Inner Product, RBF) for various architectures (ResNet18, ResNet50, ResNet101, ConvNextV2-Base, ViT-B/16, ViT-L/32, DinoV2-Giant). It compares the correlation for both permutation-invariant and non-invariant similarity measures to show the impact of spatial permutation invariance on the prediction accuracy.
In-depth insights#
Semantic RSMs#
The core idea behind Semantic RSMs is to disentangle semantic similarity from spatial information within image representations learned by neural networks. Traditional Representational Similarity Matrices (RSMs) confound these two aspects, leading to inaccurate similarity assessments when spatial arrangements differ (e.g., comparing an image to its translated version). Semantic RSMs address this by formulating similarity as a set-matching problem, focusing solely on the semantic content of the representations regardless of their spatial location. This is achieved by finding the optimal permutation of feature vectors that maximizes similarity, making the measure invariant to arbitrary spatial shifts. The method offers a more robust and accurate way to capture the true semantic understanding of a neural network, improving applications such as image retrieval and predicting class probability similarity. However, the computational complexity of finding the optimal permutation is a significant challenge, motivating the need for efficient approximation algorithms as discussed in the paper.
Spatial Decoupling#
The concept of “Spatial Decoupling” in the context of neural networks centers on disentangling semantic information from spatial location within learned representations. Current methods for measuring representational similarity often conflate these two aspects, leading to inaccurate assessments of how similar images are to a network. Spatial Decoupling aims to address this by creating a measure of similarity that is invariant to spatial transformations, such as translations or rotations. This allows for a more accurate understanding of what the network actually learns in terms of semantic features, independent of their position in an image. By isolating semantic content, we gain insights into the network’s inherent understanding of objects, irrespective of their location within the scene. This approach offers a new perspective on interpreting internal representations, leading to a more robust assessment of deep learning models and opening new avenues for analyzing and improving their performance.
Image Retrieval#
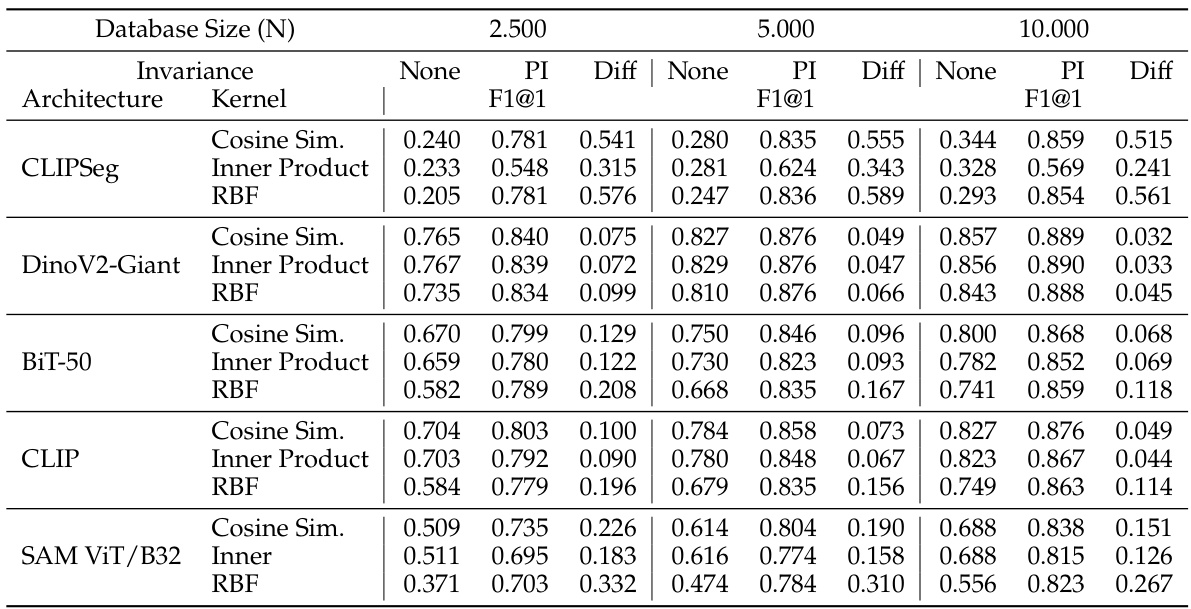
The image retrieval experiments evaluate the practical impact of the proposed semantic RSMs. Using a real-world dataset (EgoObjects), the method demonstrates superior retrieval performance compared to traditional spatio-semantic RSMs, especially when using general-purpose feature extractors like CLIP and SAM. This improvement highlights the effectiveness of decoupling semantic similarity from spatial localization. The permutation invariance introduced in semantic RSMs allows the retrieval of semantically similar images irrespective of their spatial variations. This is a significant advancement as it addresses the limitation of existing methods that heavily rely on perfect spatial alignment. The F1-score metric employed measures the overlap of annotated objects between query and retrieved images, providing a robust evaluation of retrieval accuracy even in complex scenes. Overall, these experiments confirm the effectiveness of the proposed approach for image retrieval and showcase its potential for real-world applications.
Computational Limits#
Computational limits in Representational Similarity Analysis (RSA) are significant, especially when dealing with high-dimensional data such as image representations. The primary computational bottleneck is the process of finding optimal permutations between feature vectors to ensure spatial invariance. This is an NP-hard problem, necessitating the use of approximation algorithms. The paper explores various strategies to mitigate this complexity, such as greedy matching, TopK-Greedy, and Batch-Optimal algorithms, each balancing computational cost against accuracy. The choice of approximation algorithm significantly affects both the speed and accuracy of the analysis, which is a trade-off researchers must consider carefully. The authors demonstrate that even computationally efficient methods can be successfully used to improve image retrieval and classification performance. Despite these approximations, the high dimensionality of deep learning representations inherently poses challenges, highlighting the ongoing need for more efficient computational methods in RSA to make it scalable to larger datasets and models. Future work could focus on developing faster algorithms, potentially incorporating hardware acceleration or more sophisticated approximation techniques that allow maintaining accuracy while significantly reducing the computational burden.
Future Directions#
Future research could explore more efficient approximation algorithms for semantic RSM computation, addressing the current computational bottleneck for high-resolution images. Investigating the impact of different kernel functions beyond those tested (linear, RBF, cosine) is crucial for understanding their effect on semantic similarity measurement. Furthermore, a deeper theoretical analysis of the relationship between semantic RSMs and existing representational similarity measures like CKA could reveal valuable insights. The effectiveness of semantic RSMs should be evaluated across a broader range of tasks and datasets, beyond image retrieval, to assess its generalizability and practical utility. Finally, exploring the integration of semantic RSMs with other methods for interpreting neural network representations could offer a more comprehensive understanding of deep learning models.
More visual insights#
More on figures
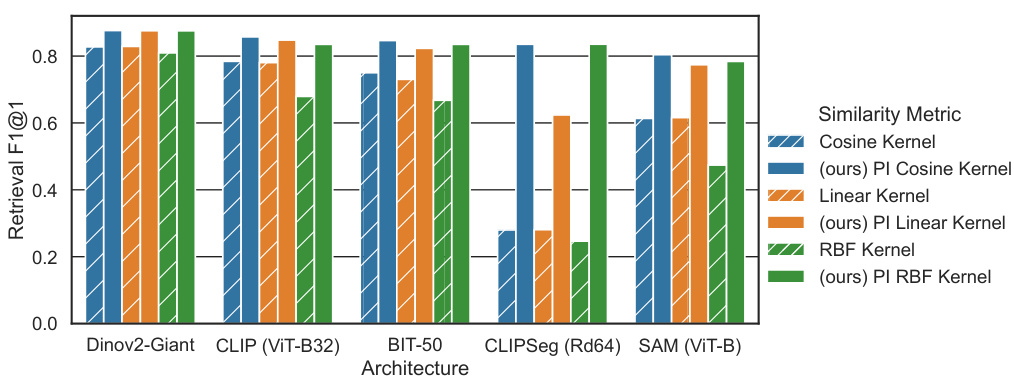
This figure shows the retrieval F1@1 scores for different architectures (Dinov2-Giant, CLIP, BiT-50, CLIPSeg, SAM) and similarity metrics (cosine kernel, permutation-invariant cosine kernel, linear kernel, permutation-invariant linear kernel, RBF kernel, permutation-invariant RBF kernel). The results demonstrate that incorporating permutation invariance improves retrieval performance across all architectures and metrics, highlighting the benefit of decoupling semantic similarity from spatial alignment.

This figure shows the top 3 most similar images retrieved using both cosine similarity and permutation-invariant cosine similarity for two example query images. The results demonstrate that permutation-invariant similarity better captures the semantic similarity between scenes, even when their spatial layouts differ significantly. This highlights the effectiveness of the proposed semantic RSM approach in overcoming the limitations of traditional spatio-semantic RSMs, which are highly sensitive to spatial alignment.
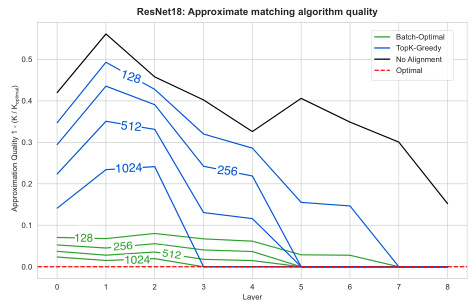
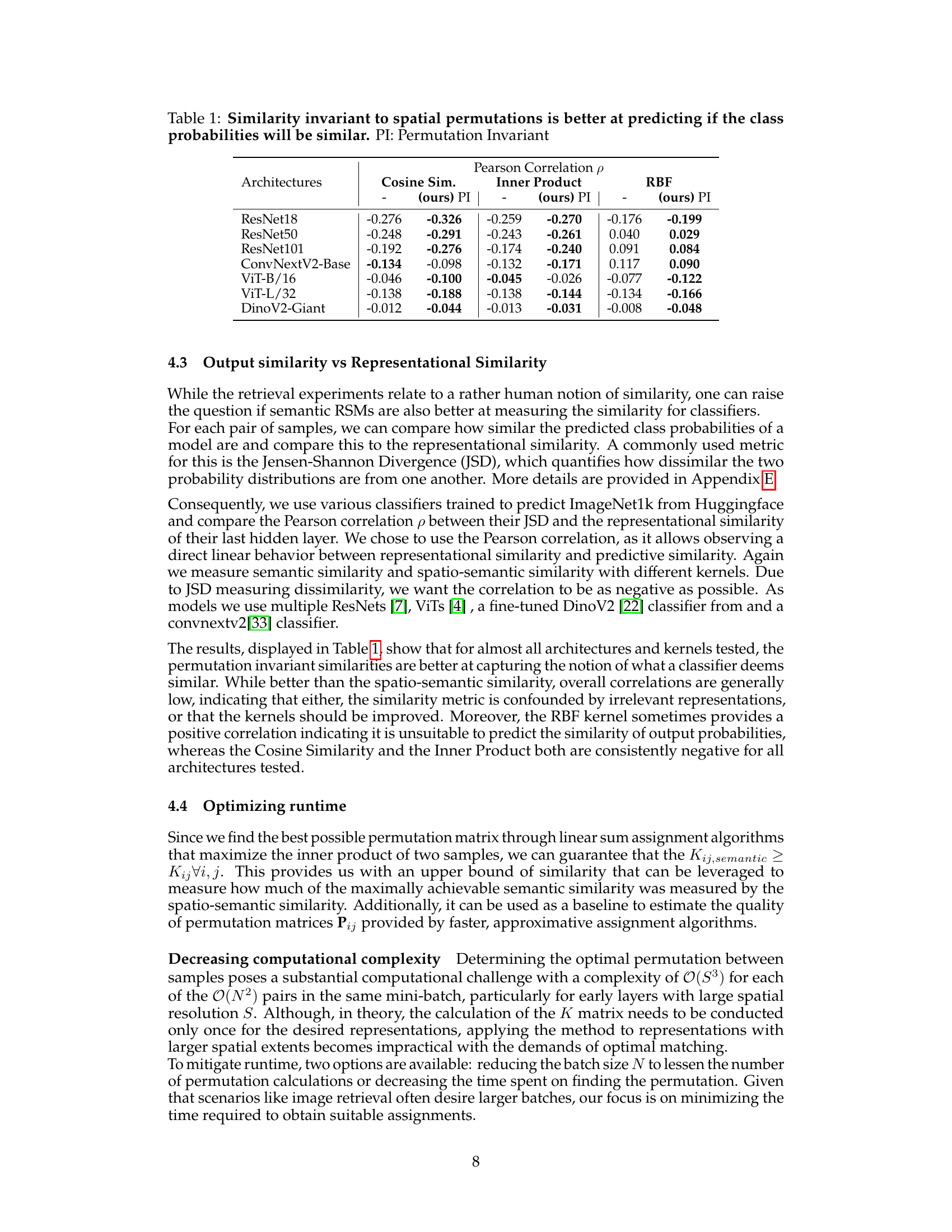
This figure shows the performance of three approximate algorithms for finding optimal permutations compared to the optimal Hungarian algorithm. The algorithms are evaluated based on the ratio of their achieved similarity to the similarity achieved by the optimal algorithm. The results demonstrate that the Batch-Optimal approximation provides a good balance between accuracy and computational efficiency, especially for layers with larger spatial dimensions. This highlights that reasonably accurate approximate algorithms can be used to reduce computation time significantly without severely impacting accuracy.
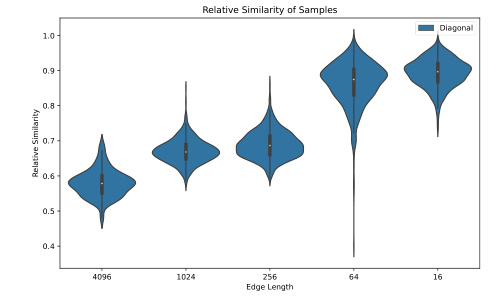
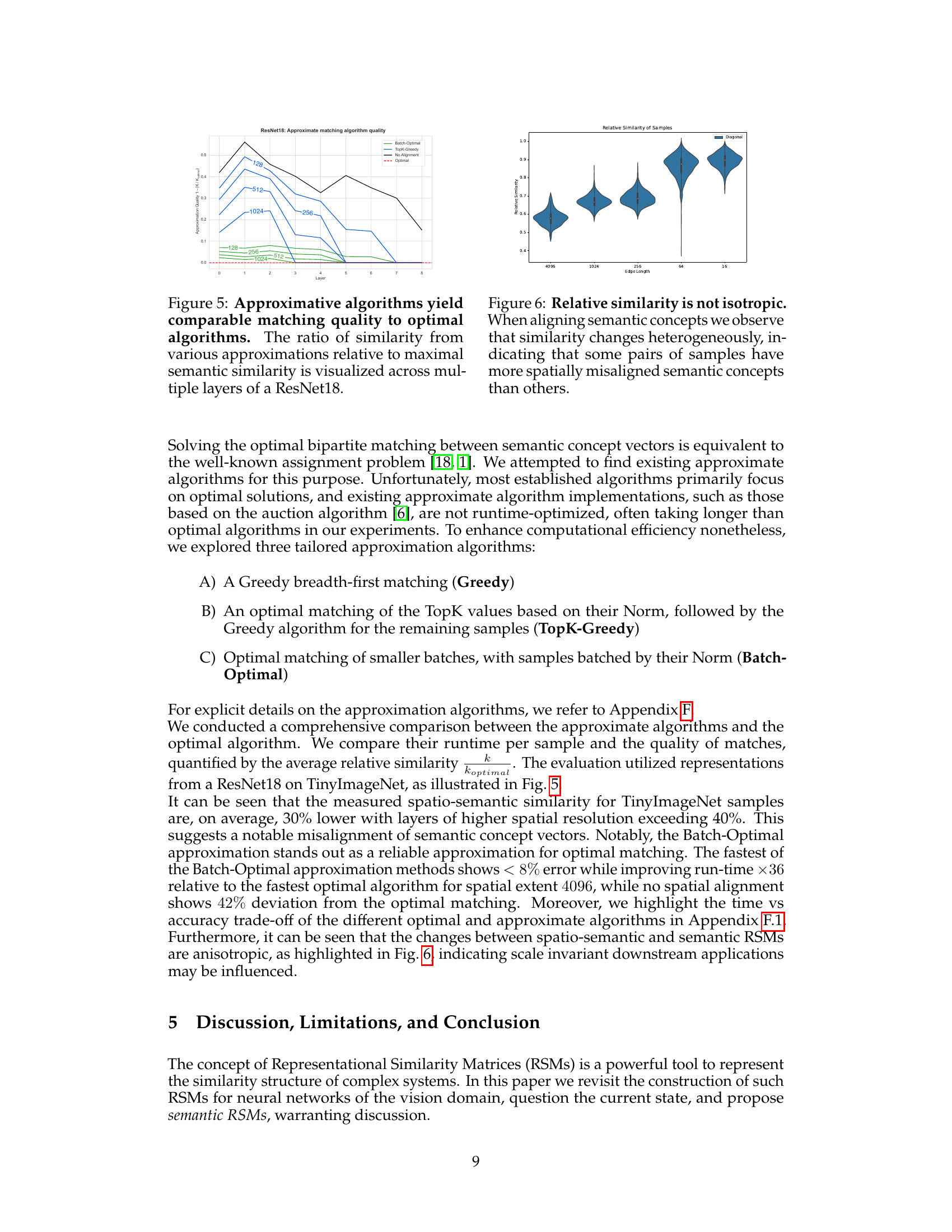
This figure demonstrates that the relative similarity between samples is not uniform across all spatial locations. Some pairs of samples show greater similarity despite having spatially misaligned semantic concepts, suggesting that semantic similarity is not solely determined by spatial alignment but other factors also contribute.
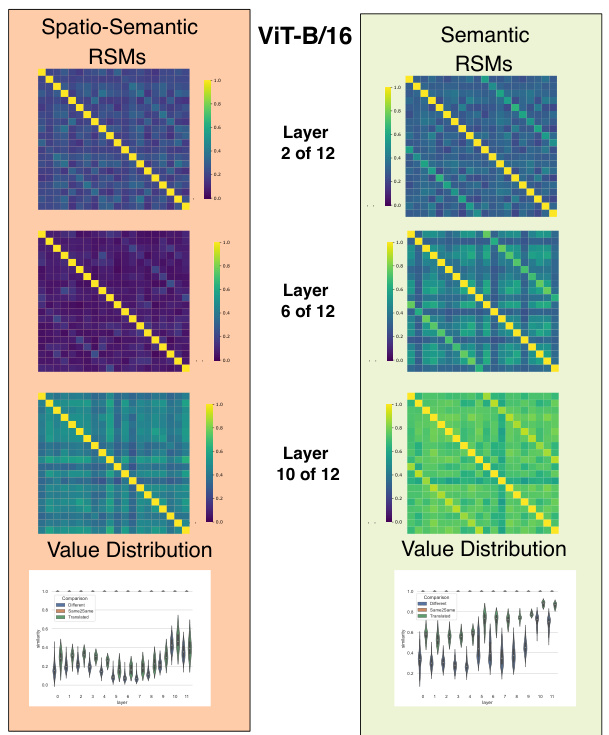
This figure compares spatio-semantic RSMs and semantic RSMs across different layers of a ResNet18 model trained on TinyImageNet. It uses partially overlapping crops of the same image to highlight the difference. Spatio-semantic RSMs struggle to identify translated versions of the same image due to their dependence on spatial alignment, while semantic RSMs effectively detect the similarity, demonstrating their spatial invariance.

This figure compares the performance of spatio-semantic RSMs and semantic RSMs in capturing similarity between images, especially when spatial alignment is altered (e.g., through translation). Using TinyImageNet, the authors generate image crops with varying degrees of overlap. The results show that semantic RSMs (the authors’ proposed method) are more robust to changes in spatial location and accurately capture semantic similarity even when images are translated, unlike the traditional spatio-semantic RSMs.

This figure compares spatio-semantic and semantic RSMs across different layers of a ResNet18 model trained on TinyImageNet. It shows that semantic RSMs (proposed method) are more effective at capturing similarity between images, even when they are spatially shifted, unlike spatio-semantic RSMs.

This figure compares the performance of spatio-semantic RSMs and semantic RSMs (proposed in the paper) across different layers of a ResNet18 model trained on TinyImageNet. Partially overlapping image crops are used as input. The results show that semantic RSMs are superior at capturing semantic similarity, even when images are translated, unlike spatio-semantic RSMs which are sensitive to spatial alignment.

This figure compares spatio-semantic and semantic RSMs across different layers of a ResNet18 model trained on TinyImageNet. Spatio-semantic RSMs show low similarity between translated versions of the same image because they couple semantic similarity with spatial alignment. In contrast, semantic RSMs are invariant to spatial permutation and successfully capture semantic similarity even when images are translated, demonstrated through enhanced off-diagonal values in the RSMs and distinct similarity value distributions.

This figure compares spatio-semantic RSMs and semantic RSMs across different layers of a ResNet18 model trained on TinyImageNet. It shows that semantic RSMs, which are invariant to spatial permutations, are better at capturing semantic similarity between images, even when they are translated versions of each other, unlike the spatio-semantic RSMs.

This figure compares spatio-semantic and semantic RSMs across different layers of a ResNet18 model trained on TinyImageNet. Spatio-semantic RSMs show low similarity between translated versions of the same image, while semantic RSMs show high similarity, highlighting their invariance to spatial shifts.

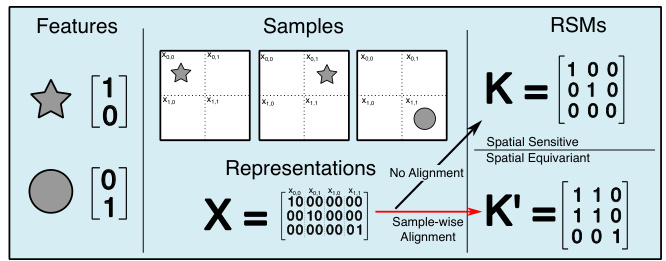
This figure illustrates the difference between traditional spatio-semantic RSMs and the proposed semantic RSMs. Spatio-semantic RSMs consider both semantic similarity and spatial alignment when comparing representations, leading to sensitivity to spatial shifts. In contrast, semantic RSMs are invariant to spatial permutations, focusing solely on semantic similarity by finding the optimal permutation between representations.

This figure compares the performance of spatio-semantic RSMs and semantic RSMs in capturing similarity between images, especially when those images are translated versions of each other. It uses TinyImageNet and a ResNet18 model. The results show that semantic RSMs, which are invariant to spatial permutations, are significantly better at capturing semantic similarity, even when spatial alignment is different.
This figure compares semantic and spatio-semantic RSMs for the same model using CKA. It shows that the dissimilarity between the two types of RSMs decreases as the spatial extent shrinks (moving from earlier to later layers). The left and middle panels show a complete layer-by-layer comparison via CKA heatmaps, while the right panel focuses on the diagonal of the CKA heatmaps to highlight the trend of decreasing dissimilarity.
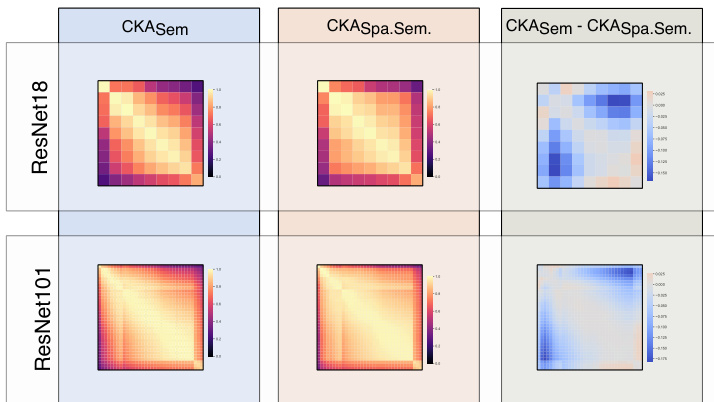
This figure compares semantic and spatio-semantic Representational Similarity Matrices (RSMs) for the same model using Centered Kernel Alignment (CKA). It shows that the dissimilarity between the two types of RSMs decreases as the spatial extent of the representations shrinks (i.e., in later layers of a CNN). The visualizations include heatmaps of the CKA values for all layers and line plots showing the diagonal of the CKA matrices, highlighting the trend of decreasing dissimilarity in later layers.
More on tables
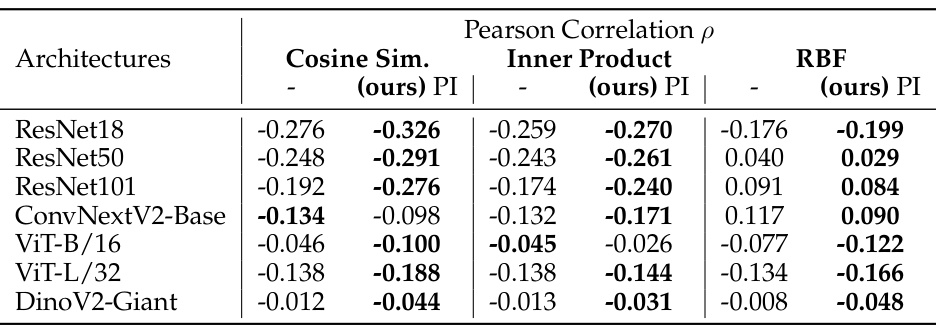
This table presents the Pearson correlation between the representational similarity (using different kernels: Cosine, Inner Product, RBF) and the Jensen-Shannon Divergence (JSD) of the predicted class probabilities for various architectures (ResNets, ConvNeXt, ViTs, DinoV2). Both permutation invariant and non-invariant similarity measures are compared to show the impact of spatial permutation invariance on predicting class probability similarity. Higher negative correlations indicate a stronger relationship, where similar representations lead to similar predicted probabilities.
This table presents the Pearson correlation between the representational similarity (using different kernels: cosine similarity, inner product, and RBF) and the Jensen-Shannon Divergence (JSD) of predicted class probabilities for various architectures (ResNet18, ResNet50, ResNet101, ConvNextV2-Base, ViT-B/16, ViT-L/32, and DinoV2-Giant). It compares the performance with and without permutation invariance to highlight the impact of spatial alignment on the prediction similarity.
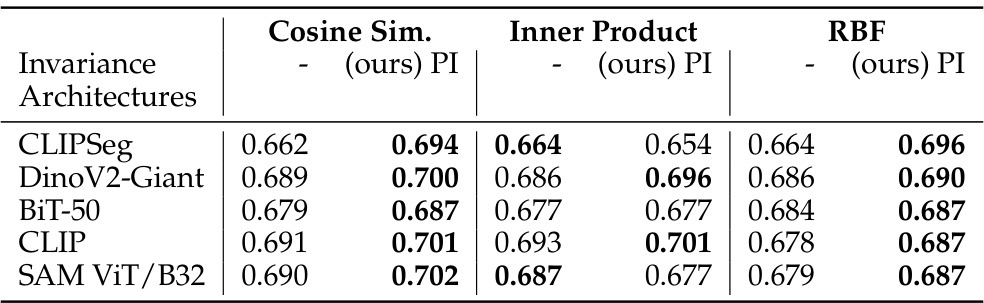
This table presents the quantitative results of a retrieval experiment using the Cityscapes dataset. It compares the performance of different similarity metrics (Cosine Similarity, Inner Product, RBF) with and without permutation invariance. The results show that permutation invariance consistently improves retrieval performance, especially for Cosine Similarity and RBF.
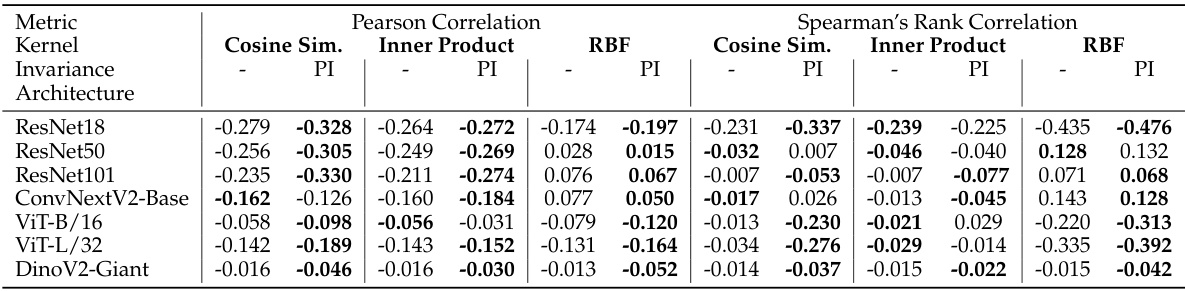
This table presents the Pearson and Spearman correlations between the representational similarity (using different kernels and with/without permutation invariance) and the similarity of predicted class probabilities for various ImageNet classifiers. Higher negative correlations indicate stronger agreement between the two types of similarity.
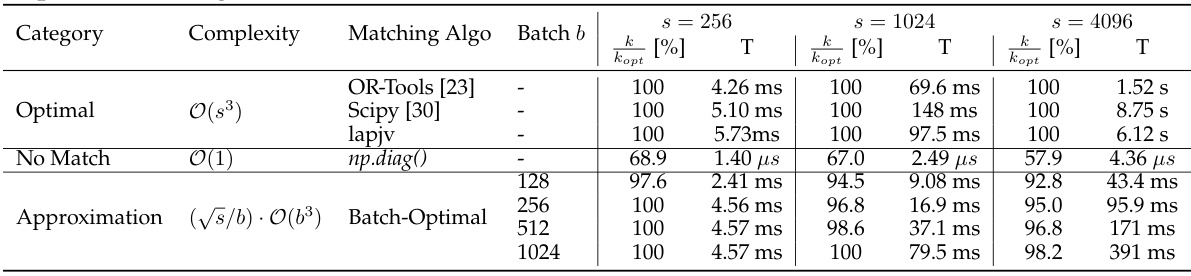
This table compares the runtime and matching quality of different algorithms for solving the assignment problem, a key step in the proposed semantic RSM calculation. It shows that a proposed approximation algorithm, Batch-Optimal, achieves near-optimal matching quality with significantly reduced runtime compared to exact methods, especially beneficial for larger spatial dimensions. The ‘No Match’ row serves as a baseline representing the scenario without any matching.
Full paper#