↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multi-view depth estimation is crucial for various applications, but existing methods often struggle with robustness and accuracy, especially when dealing with real-world data. Many approaches lack
equivariance, meaning their predictions change inconsistently when the viewpoint or object orientation changes. This issue is typically addressed through data augmentation, which can be inefficient and lead to inconsistencies.
This research introduces a novel approach that directly embeds SE(3) equivariance into the Perceiver IO architecture. The authors use spherical harmonics for positional encoding and develop a specialized equivariant encoder and decoder to ensure that the model’s output is consistent regardless of the reference frame. This leads to improved accuracy and robustness, particularly for real-world scenarios. The method achieves state-of-the-art performance on benchmark datasets without extensive data augmentation.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the limitations of existing multi-view depth estimation methods by incorporating SE(3) equivariance into the Perceiver IO architecture. This leads to more robust and accurate depth estimations, especially on real-world datasets, and opens new avenues for research in 3D scene understanding and other related fields that require robust multi-view representations.
Visual Insights#

This figure compares the performance of a standard Perceiver IO model versus the proposed equivariant Perceiver IO model for multi-view depth estimation. Both models receive the same sparse set of input images. The key difference is that the standard Perceiver IO model is not equivariant with respect to changes in the reference frame (a global transformation applied to the object and cameras). The equivariant Perceiver IO model, in contrast, is robust to such transformations, providing consistent depth predictions regardless of the reference frame.

This table compares the performance of the proposed Equivariant Perceiver IO (EPIO) model against its non-equivariant baseline, DeFiNe, on the ScanNet dataset. It specifically investigates the impact of two types of data augmentation techniques: virtual camera augmentation (VCA) and canonical camera jittering. The results are presented in terms of three commonly used metrics for evaluating stereo depth estimation performance: Absolute Relative Error (Abs.Rel.), Root Mean Squared Error (RMSE), and the percentage of pixels with a delta error less than 1.25 (δ < 1.25). By comparing performance across different augmentation strategies, the table aims to showcase the advantages of incorporating equivariance into the model for improving robustness and generalization.
In-depth insights#
SE(3) Equivariance#
The concept of SE(3) equivariance is central to this research, signifying the model’s ability to maintain consistent predictions regardless of the coordinate system’s orientation and position. Achieving SE(3) equivariance is particularly challenging in multi-view 3D learning, where transformations of the scene affect input data differently across viewpoints. The authors address this by embedding SE(3) equivariance directly into the architecture, not relying on data augmentation which can introduce inconsistencies. This is achieved through the use of spherical harmonics for positional encoding, which provides a 3D rotation-equivariant representation, and the design of a specialized equivariant encoder and decoder within the Perceiver IO framework. This design ensures that the model’s output transforms correctly when the scene is rotated or translated. The result is a robust and accurate depth estimation model, exhibiting state-of-the-art performance even in challenging scenarios, highlighting the substantial advantages of integrating equivariance into 3D deep learning models.
Implicit Geometry#
Implicit geometry leverages the power of neural networks to learn and represent geometric structures without explicitly defining them. Instead of relying on explicit geometric primitives, like meshes or point clouds, implicit methods learn a function that maps coordinates to properties such as occupancy or distance. This is particularly powerful for multi-view scenarios where integrating geometric information from various viewpoints is a challenge. The strength of implicit geometry lies in its ability to handle complex shapes and noise, and its adaptability to various tasks such as depth estimation and scene reconstruction. Implicit methods typically utilize neural networks to represent complex geometric entities. However, a key challenge is maintaining equivariance, ensuring that the representation transforms consistently with the geometric transformation of the underlying object. Addressing this challenge is crucial for robustness and generalization across different coordinate systems, improving the quality and reliability of 3D reconstructions.
Spherical Harmonics#
The application of spherical harmonics in this research stands out for its elegant solution to the problem of rotational equivariance in 3D space. Unlike traditional Fourier-based positional encodings, spherical harmonics inherently possess rotational equivariance, making them ideally suited for representing 3D orientations and rotations of geometric entities such as rays and cameras. This choice directly addresses the limitations of previous work that relied on data augmentation to achieve approximate equivariance, leading to inconsistencies across different reference frames. By leveraging the inherent properties of spherical harmonics, the model’s architecture ensures that the outputs remain consistent regardless of global coordinate frame transformations, thus enhancing the robustness and generalizability of the depth estimation model. The researchers’ custom design of an SE(3) equivariant attention module and the use of specialized equivariant layers further solidify the role of spherical harmonics in building an architecture that seamlessly integrates geometric information and visual features for robust multi-view 3D scene understanding.
Equivariant Modules#
Equivariant modules are crucial for building neural networks that exhibit geometric invariance. They ensure that the network’s output remains consistent even when the input undergoes transformations like rotations or translations. This is achieved by incorporating group-theoretic principles into the network architecture, allowing it to learn representations that respect the symmetries of the problem. In the context of a 3D scene understanding task such as depth estimation from multiple views, equivariant modules are essential for achieving robustness. They mitigate the issues of inconsistencies arising from different reference frames, thereby enhancing the reliability of the model’s predictions. The choice of specific equivariant modules and the way they interact with other components of the network are critical factors in determining the overall performance and generalization capabilities of the system. Developing efficient and effective equivariant modules is a key research challenge, and improvements in this area can lead to significant advancements in various computer vision applications.
Future of EPIO#
The Equivariant Perceiver IO (EPIO) model presents a significant advancement in multi-view depth estimation by integrating SE(3) equivariance. Future development could focus on enhancing its efficiency and scalability, perhaps through optimized attention mechanisms or more efficient implementations of spherical harmonics. Extending EPIO to handle more complex 3D scene understanding tasks beyond depth estimation, such as semantic segmentation or object detection, would be valuable. Exploring different architectural choices for the equivariant components may yield performance improvements and could investigate the use of other equivariant layers or network designs. Addressing the limitations of spherical harmonics regarding high-frequency information and the computational cost of high-order harmonics is crucial. A robust comparative analysis against state-of-the-art methods on a wider variety of datasets would solidify EPIO’s position in the field. Finally, investigating the potential for transfer learning and pre-training strategies for EPIO could significantly reduce the need for large, annotated datasets, making the model more accessible and practical.
More visual insights#
More on figures

This figure illustrates the architecture of the proposed Equivariant Perceiver IO (EPIO) model. It shows the input embeddings (a), the equivariant encoder producing global invariant and equivariant latents (b), how the query camera’s pose becomes invariant in the equivariant frame (c), and finally, the decoder generating predictions from the invariant latent and pose (d). Spherical harmonics are used for ray and camera positional embeddings to ensure rotational equivariance. The model disentangles the equivariant frame and invariant scene representation for efficient and robust depth estimation.

This figure compares the equivariant input embedding used in the proposed model with the conventional input embedding used in DeFiNe. It shows how the proposed model generates geometric information using embeddings for rays and relative camera positions, resulting in both invariant and equivariant components, while DeFiNe uses Fourier positional encodings and absolute camera translations.

This figure shows the architecture of the proposed Equivariant Perceiver IO (EPIO) model for multi-view depth estimation. It illustrates the flow of information through the encoder and decoder, highlighting the use of spherical harmonics for positional encoding, the separation of invariant and equivariant components in the latent space, and the use of a conventional Perceiver IO decoder for prediction.

This figure shows the effect of object rotation on the equivariant latent code and the predicted canonical frame. The top row illustrates the predicted frame (in blue) and its rotation relative to the object (in gray). The middle row shows the object model and its rotation. The bottom row visualizes the latent code as a spherical function, demonstrating its rotation alongside the object and the predicted frame, highlighting the equivariance property of the model. In essence, it shows the consistency of predictions regardless of the reference frame.

This figure showcases a comparison of stereo depth estimation results on the ScanNet dataset between the proposed Equivariant Perceiver IO (EPIO) model and the non-equivariant baseline (DeFiNe). Three rows present different scenes from the dataset. Each row shows the input images, the ground truth depth map, the depth map generated by DeFiNe, and the depth map produced by the EPIO model. The figure visually demonstrates the superior performance of the EPIO model in accurately estimating depth compared to the baseline, highlighting the benefits of incorporating SE(3) equivariance.

This figure shows a comparison between a standard Perceiver IO model and the proposed equivariant model for multi-view depth estimation. The Perceiver IO model struggles to maintain consistent depth prediction accuracy when the camera’s reference frame changes, while the equivariant model produces consistent results even with reference frame changes. This demonstrates the benefit of incorporating SE(3) equivariance into the architecture.
This figure shows the architecture of the proposed Equivariant Perceiver IO (EPIO) model for multi-view depth estimation. It details the input embeddings (image, ray, camera), the equivariant encoder generating invariant and equivariant latent codes, the extraction of an equivariant reference frame, and the use of a conventional decoder for final predictions. The model leverages spherical harmonics for positional encoding to achieve SE(3) equivariance.
This figure illustrates the architecture of the proposed Equivariant Perceiver IO (EPIO) model for multi-view depth estimation. It shows the input processing, which includes image, ray, and camera embeddings (a), the equivariant encoder generating global invariant and equivariant latents (b), the extraction of an equivariant reference frame and invariant latents (b), the use of an invariant query camera pose and Fourier encoding (c), and finally, the use of a conventional Perceiver IO decoder to generate predictions (d).

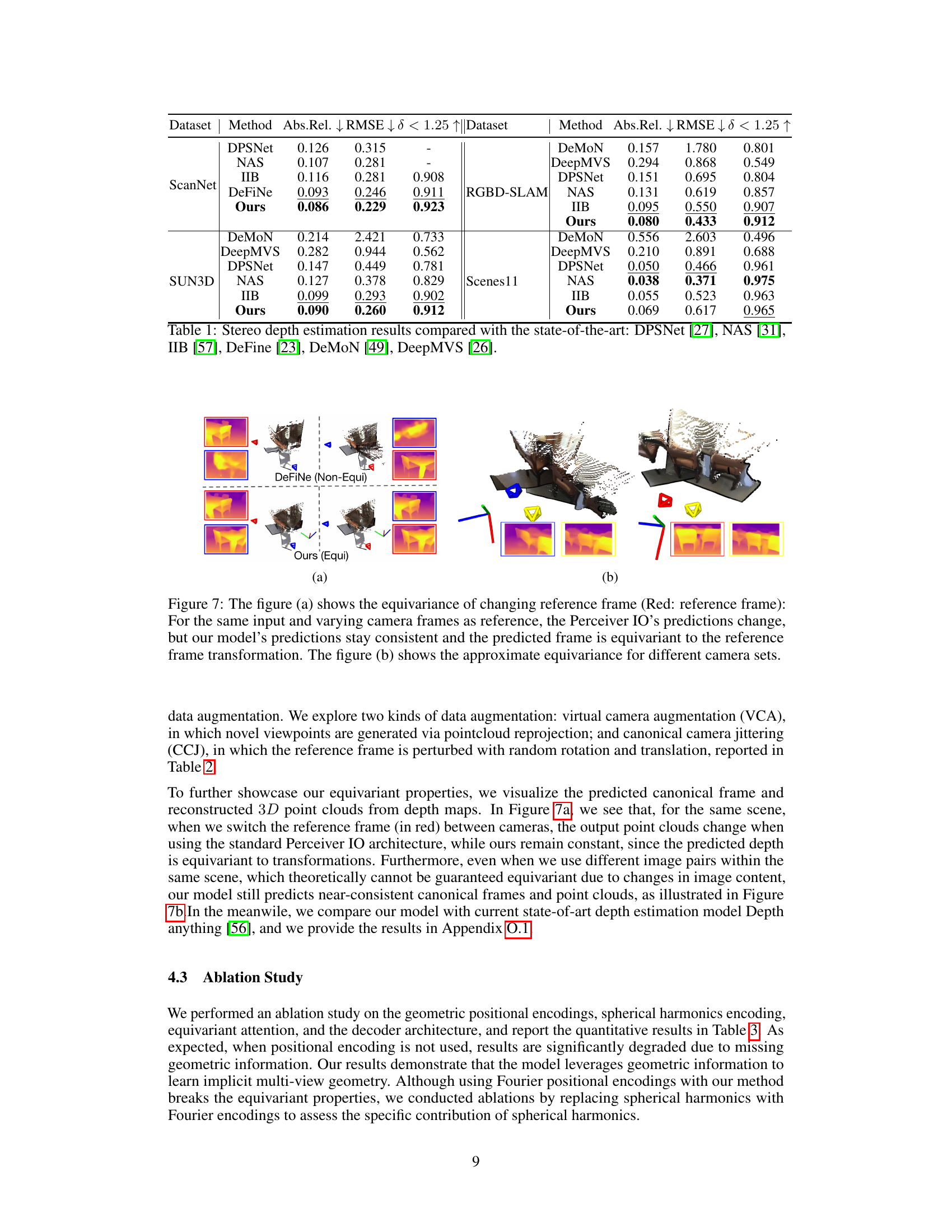
This figure illustrates how a rotation R transforms the equivariant latent code. The latent code is structured as a concatenation of features with different SO(3) transformation properties. Each feature type, represented as Hi, undergoes a transformation by the corresponding Wigner-D matrix D¹(R). This demonstrates the equivariance of the latent representation.

This figure illustrates the architecture of the proposed Equivariant Perceiver IO (EPIO) model for multi-view depth estimation. It shows the input stage combining image, ray, and camera embeddings; the equivariant encoder generating global invariant and equivariant latents; the extraction of an equivariant reference frame; and finally, the decoder using a conventional Perceiver IO architecture to produce predictions based on invariant latent and pose information.
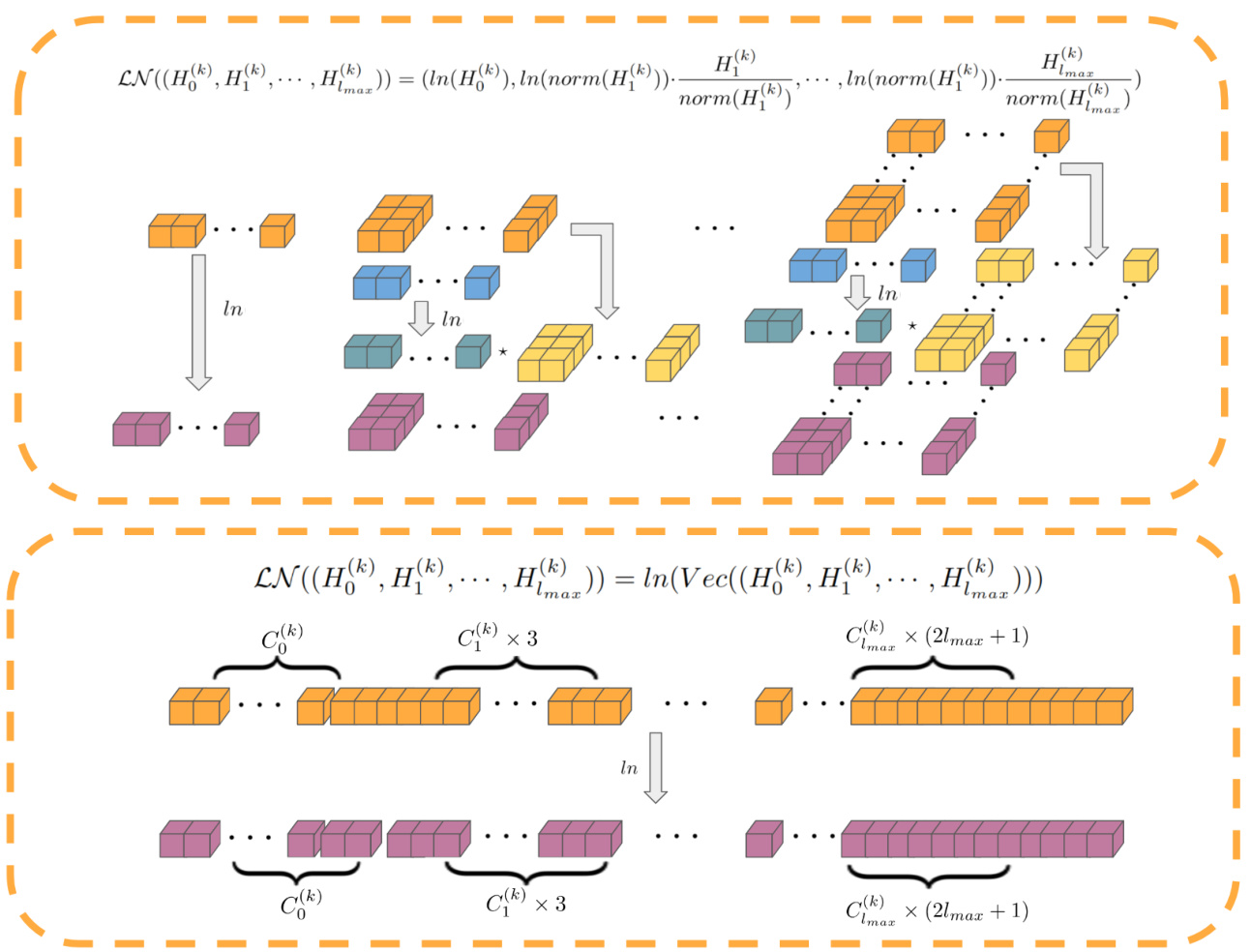
The figure illustrates the equivariant decoder architecture. It shows how the equivariant latent features from the encoder, along with equivariant positional encodings of query rays and camera poses, are processed through a series of equivariant linear layers and a multi-head attention mechanism to generate equivariant output features (00, 01,…, Olmax). These are then converted to invariant features (O'0) through an invariant layer. The process ensures that the output remains consistent regardless of changes in global reference frame.

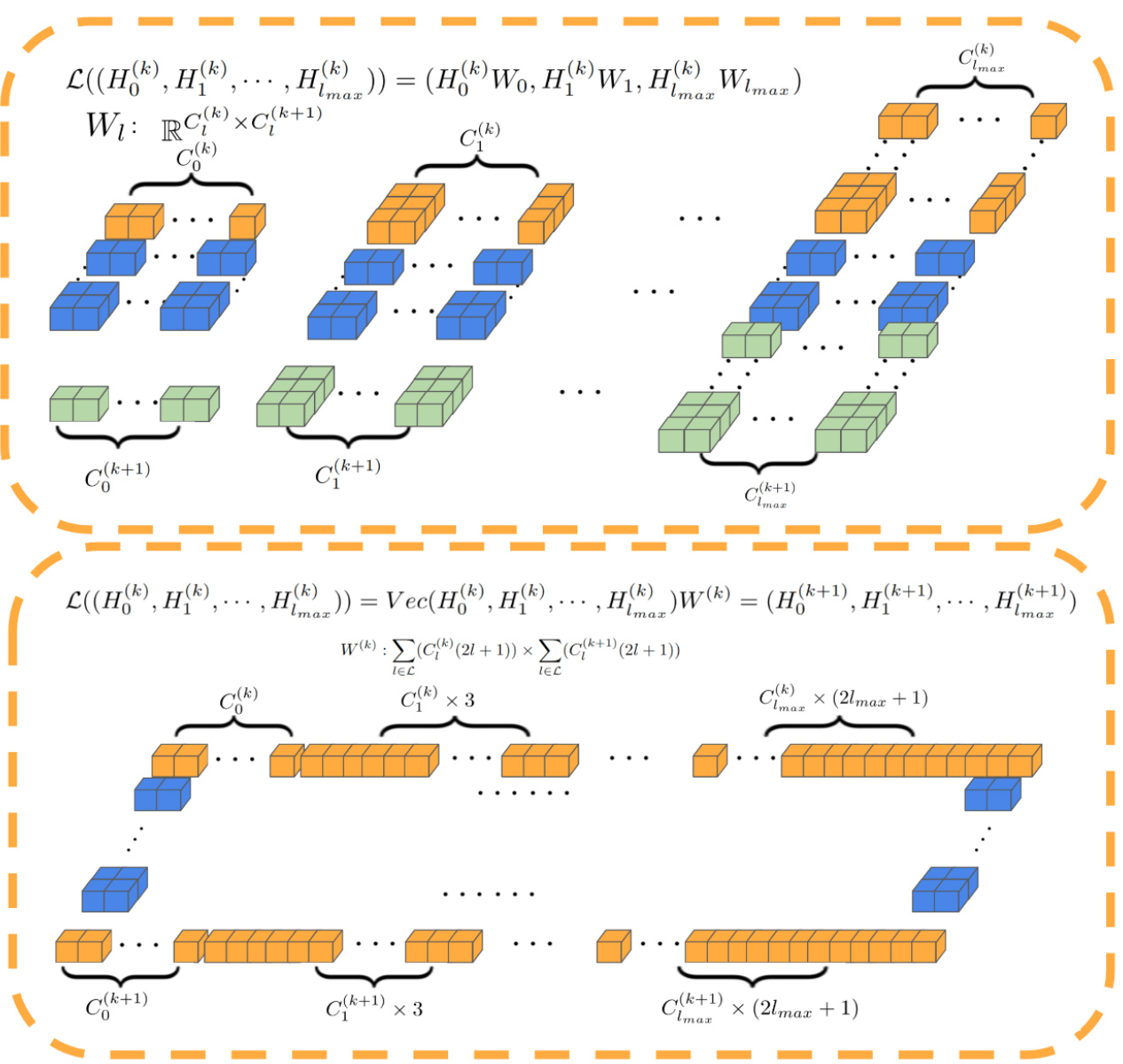
This figure shows the architecture of the invariant layer used in the decoder. It takes equivariant features as input and transforms them into invariant features using equivariant linear layers and inner product operations. The output is a set of invariant features that are used for final prediction.

This figure shows a qualitative comparison of depth estimation results on the ScanNet dataset. It presents input images from two viewpoints, the ground truth depth map, and the depth maps generated by the DeFiNe (Non-Equi) baseline and the proposed EPIO (Equi) model. The EPIO model shows improved performance in accurately estimating depth compared to the baseline, particularly in capturing fine details and handling challenging regions.
More on tables
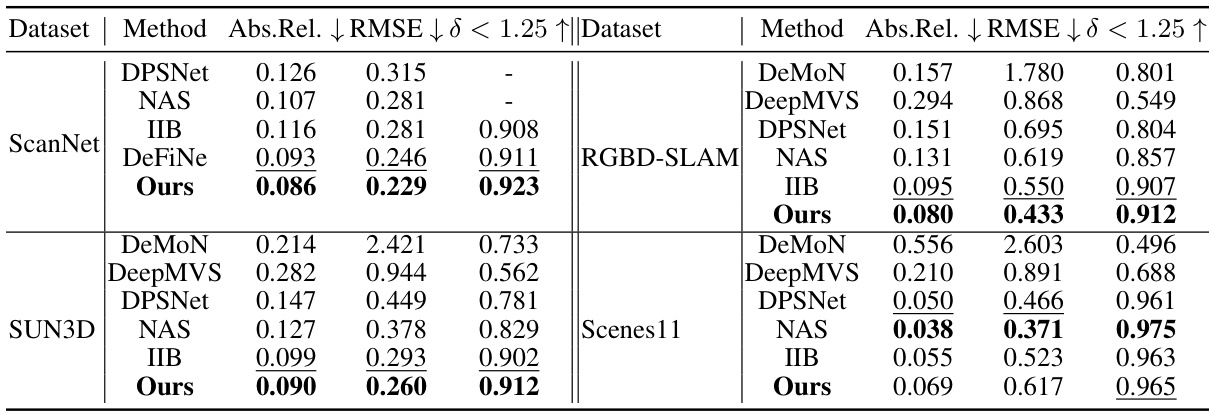
This table presents a comparison of the proposed Equivariant Perceiver IO (EPIO) model’s performance on stereo depth estimation against several state-of-the-art methods. The results are shown across three standard metrics (Abs.Rel, RMSE, δ<1.25) and three datasets (ScanNet, SUN3D, Scenes11). It highlights the superior performance of EPIO, particularly on real-world datasets (ScanNet, SUN3D).
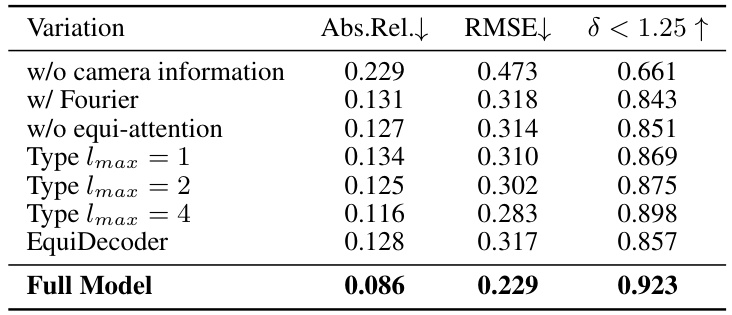
This table presents the results of an ablation study conducted to evaluate the impact of different design choices on the performance of the proposed model. Specifically, it analyzes the effects of removing camera information, using Fourier encodings instead of spherical harmonics, removing the equivariant attention module, varying the maximum order of spherical harmonics (lmax), and using a non-equivariant decoder. The results are reported in terms of three metrics: Absolute Relative error (Abs. Rel.), Root Mean Squared Error (RMSE), and the percentage of pixels with error less than 1.25 (δ < 1.25). The comparison allows for assessing the individual contribution of each component towards achieving state-of-the-art results.

This table shows how the proposed Equivariant Perceiver IO (EPIO) architecture can be adapted to various computer vision tasks. It lists the input data, the type of geometric transformation involved, the type of positional encoding used, the feature embedding method, the query type, and the prediction type for each task. This illustrates the model’s flexibility and generalizability across a range of problems.
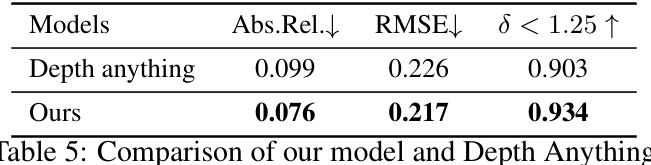
This table presents a quantitative comparison of the proposed SE(3) Equivariant Perceiver IO model against the Depth Anything model on the ScanNet benchmark. The metrics used for comparison are Absolute Relative Error (Abs.Rel.), Root Mean Squared Error (RMSE), and the percentage of pixels with error less than 1.25 (δ < 1.25). Lower values of Abs.Rel. and RMSE indicate better accuracy, while a higher value for δ < 1.25 signifies a greater proportion of pixels with accurate depth predictions. The results demonstrate that the proposed model outperforms Depth Anything on all three metrics.

This table presents a comparison of depth estimation results obtained using the DeFiNe and the proposed Equivariant Perceiver IO (EPIO) models. The results are evaluated across different numbers of input views (2, 3, and 4) to illustrate the impact of the number of views on depth estimation accuracy. Lower values indicate better performance.
Full paper#