↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Counterfactual reasoning, crucial for causal inference, faces computational challenges, especially when dealing with high-dimensional or complex data. Existing importance sampling methods often struggle with efficiency and variance issues, hindering practical applications. Many also require multiple rounds of proposal learning, increasing computational cost.
This paper introduces Exogenous Matching, a novel importance sampling method that addresses these issues. It minimizes variance by transforming the problem into learning a conditional distribution, allowing for efficient estimation of counterfactual expressions. The method is validated through experiments on various structural causal models (SCMs) showing its superiority and improved scalability, particularly when structural prior knowledge is integrated.
Key Takeaways#
Why does it matter?#
This paper presents a novel and efficient importance sampling method for estimating counterfactual expressions, addressing the computational challenges in causal inference. It offers a tractable solution applicable to various settings and outperforms existing methods, making it valuable for researchers in causal inference and related fields.
Visual Insights#
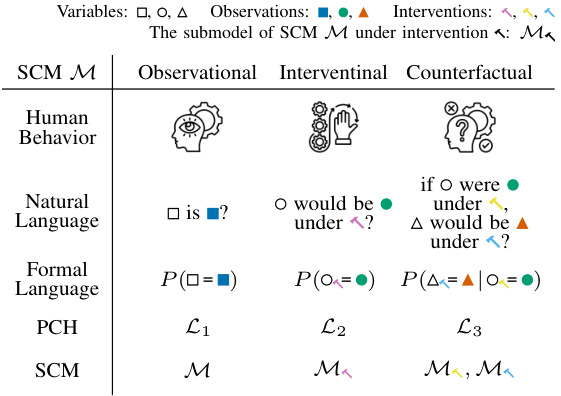
This figure illustrates the relationship between Structural Causal Models (SCMs), the Pearl Causal Hierarchy (PCH), and counterfactual reasoning. It shows how SCMs represent causal relationships between variables. The PCH organizes three levels of causal reasoning: observational (what is), interventional (what would happen if we intervened), and counterfactual (what would have happened if something different had occurred). The figure uses icons to represent human behavior (observation, intervention, and counterfactual reasoning) and formal language representations (probabilities of observational, interventional, and counterfactual events).
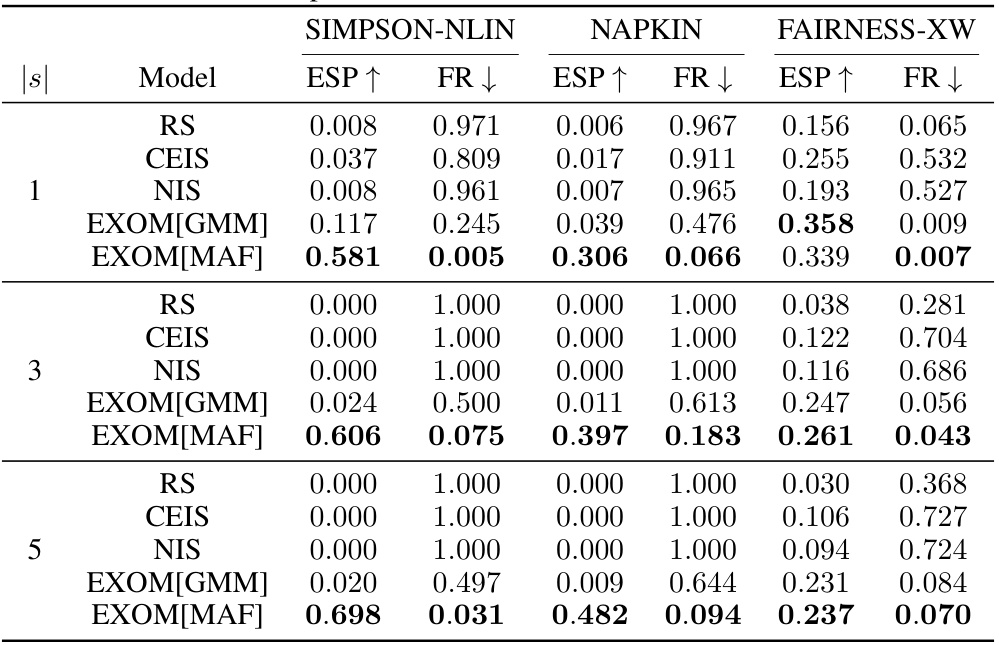
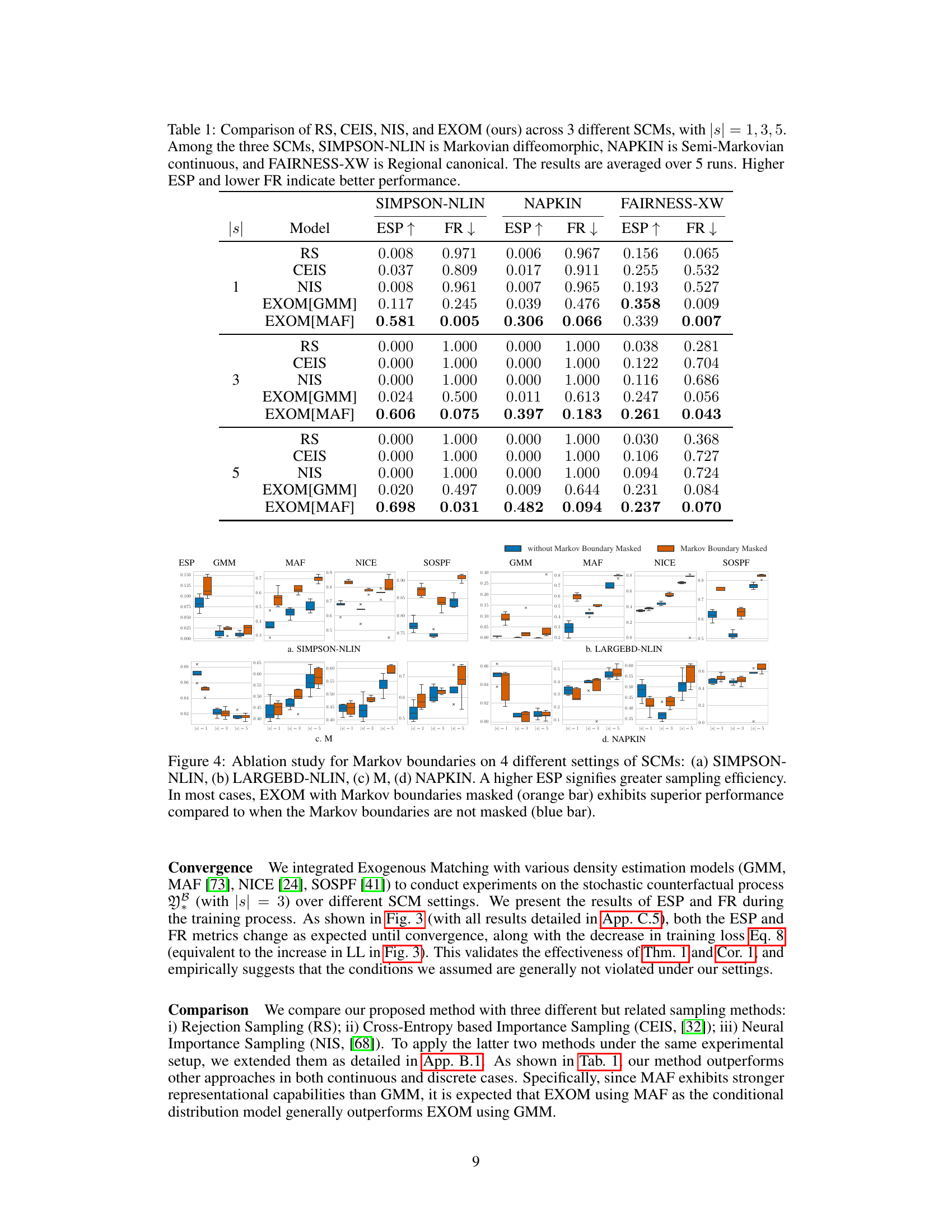
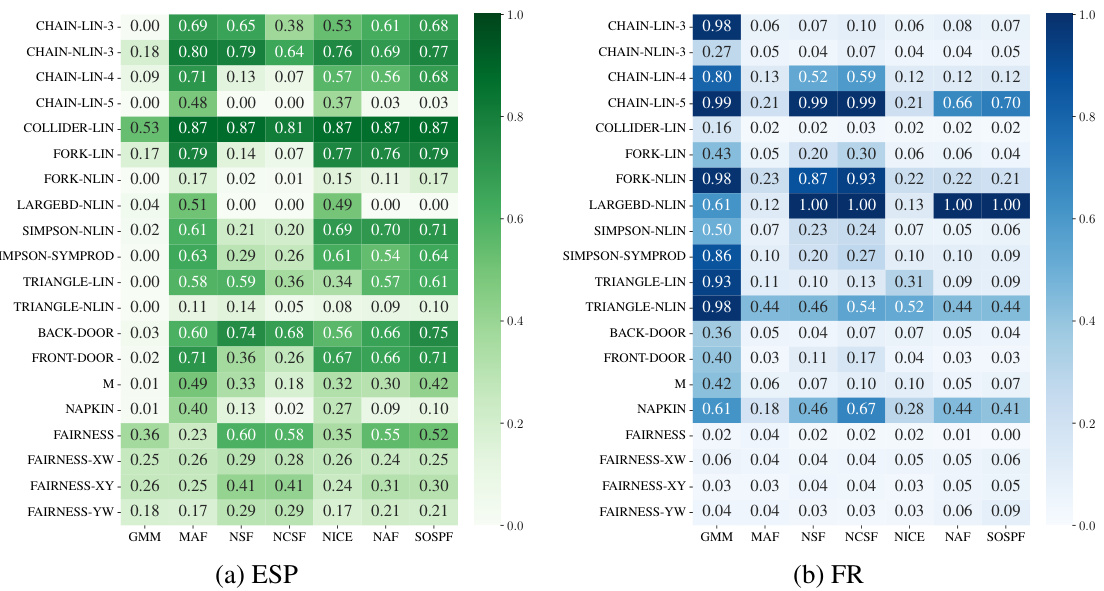
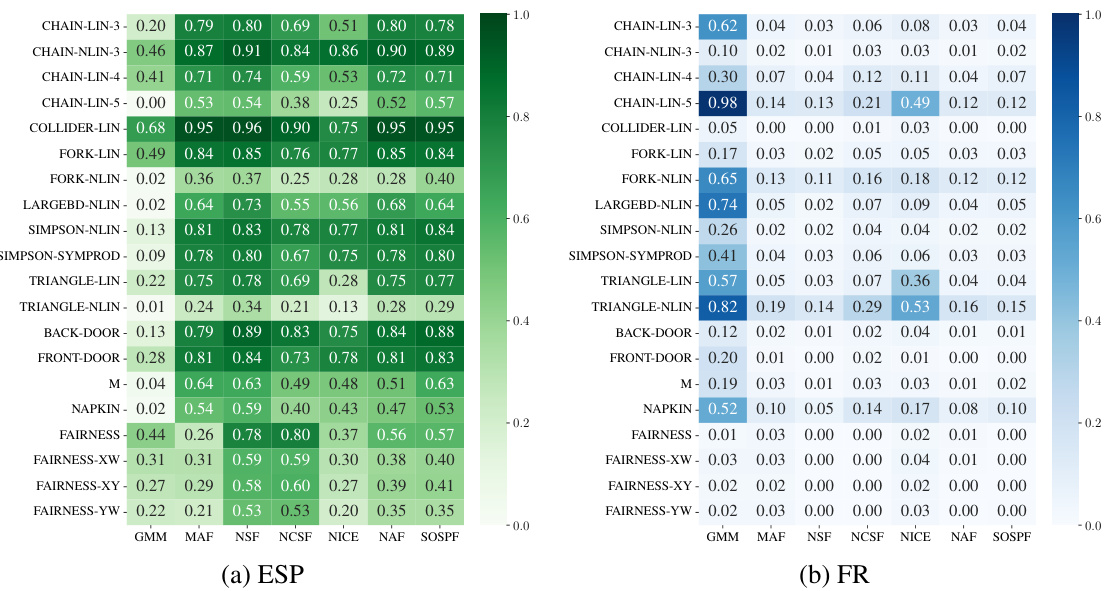
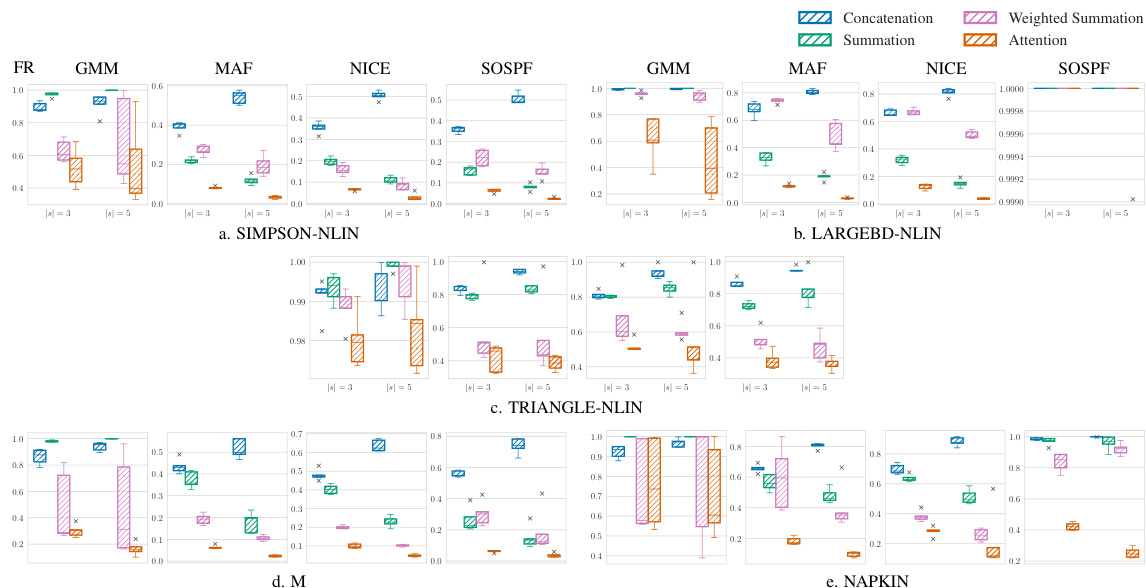
This table compares the performance of four different counterfactual estimation methods (Rejection Sampling, Cross-Entropy Importance Sampling, Neural Importance Sampling, and the proposed Exogenous Matching) across three different types of Structural Causal Models (SCMs) and for different numbers of submodels (|s|). The SCMs represent different levels of complexity and assumptions (Markovian diffeomorphic, Semi-Markovian continuous, and Regional canonical). The metrics used are Effective Sample Proportion (ESP) and Failure Rate (FR), which measure sampling efficiency and success rate, respectively. Higher ESP and lower FR values indicate better performance.
In-depth insights#
Exogenous Matching#
The proposed importance sampling method, “Exogenous Matching,” offers a novel approach to counterfactual estimation by framing the variance minimization problem as a conditional distribution learning problem. This clever transformation allows integration with existing conditional density models, significantly enhancing the tractability and efficiency of the estimation process. The core innovation is in optimizing a common upper bound on the variance of counterfactual estimators, thus learning a proposal distribution that effectively reduces variance and improves sampling efficiency. By framing the problem in this way, Exogenous Matching can handle various SCM settings, including those with discrete or continuous exogenous variables and complex counterfactual expressions. Injecting structural prior knowledge, such as counterfactual Markov boundaries, further refines the method’s performance, demonstrating the value of incorporating domain expertise into the learning process. The empirical evaluations across different SCM types highlight Exogenous Matching’s superiority over existing importance sampling methods, particularly in cases involving multiple hypothetical worlds. While assumptions such as recursiveness and computability of SCM mechanisms are made, the approach’s flexibility and scalability represent substantial advancements in counterfactual estimation.
Variance Optimization#
The concept of variance optimization is crucial in importance sampling methods, particularly when dealing with rare events. The goal is to find a proposal distribution that minimizes the variance of the importance sampling estimator, thus increasing efficiency. Minimizing variance is equivalent to concentrating the proposal distribution’s density on the regions where the target distribution’s density is high, improving sampling efficiency. The authors cleverly transform the variance minimization problem into a conditional distribution learning problem, allowing them to leverage the power of existing conditional density models. This approach offers significant advantages over traditional importance sampling methods which often struggle with high dimensionality or complex target distributions. The use of an upper bound on the variance as the optimization objective is a particularly elegant aspect of the method, enabling tractability and preventing the need for multiple rounds of optimization. This optimization objective, related to cross-entropy, is readily optimizable using various machine learning techniques, making the method practical for use in complex real-world scenarios. This approach is highly innovative and addresses limitations of previous methods, leading to substantial improvements in counterfactual estimation.
Markov Boundaries#
The concept of ‘Markov Boundaries’ in the context of causal inference and structural causal models (SCMs) is crucial for efficient counterfactual estimation. Markov boundaries represent a minimal set of variables that shield a target variable from the influence of all other variables within the model. This is especially important in the context of counterfactual reasoning, as it allows for simplification of calculations by focusing on a subset of relevant variables. By incorporating counterfactual Markov boundaries into importance sampling techniques, one can significantly improve the efficiency and tractability of counterfactual estimation. Identifying these boundaries can be done using various graph-based algorithms, making use of the causal graph structure and conditional independence properties. The inclusion of such prior knowledge into the model often results in reduced computational costs and enhanced estimation accuracy. However, obtaining or estimating these boundaries accurately might pose a challenge in cases with complex causal structures or the presence of latent confounders. The effectiveness of leveraging Markov boundaries hinges on the faithfulness assumption, which implies a direct correspondence between conditional independence and d-separation in the causal graph. Violations of this assumption could lead to suboptimal or inaccurate results.
Proxy SCMs#
The concept of ‘Proxy SCMs’ (Proxy Structural Causal Models) in the research paper represents a crucial methodological innovation for tackling the challenges of counterfactual estimation. Instead of directly working with complex, potentially unidentifiable SCMs, the authors leverage the power of neural networks to build more tractable approximations. These proxy SCMs, trained on observational data, learn to mimic the causal mechanisms of the original SCMs. This approach bypasses the computational complexities and identifiability issues often associated with exact counterfactual inference. The effectiveness of using proxy SCMs is directly tied to their ability to capture the underlying causal relationships accurately. A key consideration is thus the choice and training of neural networks capable of both expressiveness and identifiability. The paper likely explores specific neural network architectures, emphasizing techniques like normalizing flows or variational autoencoders, known for their ability to efficiently model complex probability distributions. The success of this proxy approach depends on the quality and fidelity of the proxy SCMs. The authors will assess this through comparative evaluations with alternative methods, possibly highlighting the trade-off between tractability and accuracy.
Future Directions#
The paper’s core contribution is a novel importance sampling method for counterfactual estimation. Future work could explore several avenues. Extending the method to non-recursive SCMs is crucial for broader applicability. The current reliance on recursive SCMs limits its applicability to real-world scenarios with complex cyclical causal relationships. Improving scalability to high-dimensional data is also important. The current method’s efficiency in handling many variables or high-dimensional data needs further investigation. While the method uses neural networks, exploring alternative models for conditional distribution learning could lead to performance gains and improved robustness. This includes researching advanced architectures or methods beyond MLPs and normalizing flows. Addressing the boundedness condition on importance weights is essential to improve reliability and reduce the risk of bias, especially in scenarios with infinite support. The theoretical results and experiments could be enhanced by rigorous statistical analysis. Finally, applying the method to a wider range of real-world problems is crucial. Demonstrating its efficacy on diverse applications, along with comprehensive benchmarking against existing methods will validate its practical impact. The limitations discussed provide a good starting point for these future research directions.
More visual insights#
More on figures
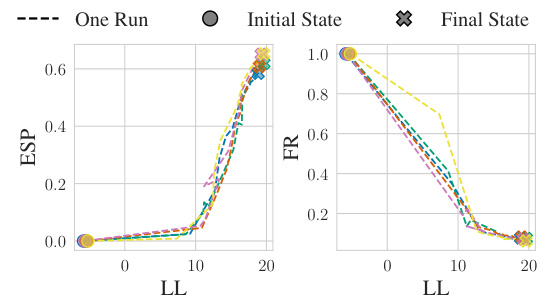
This figure shows the relationship between the negative log-likelihood (LL, which is the optimization objective), effective sample proportion (ESP), and failure rate (FR) during the training process of the Exogenous Matching (EXOM) method on the SIMPSON-NLIN structural causal model (SCM). As the LL increases (meaning the model is learning better), the ESP also increases (indicating higher sampling efficiency), and the FR decreases (meaning fewer samples are wasted because the method is better at concentrating on the important regions of the sample space). The figure demonstrates the convergence of the EXOM method.

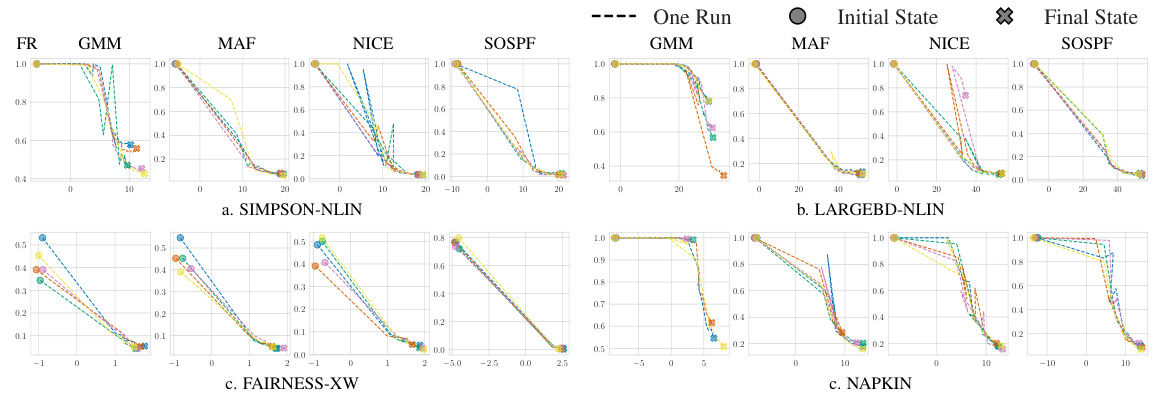
This ablation study compares the performance of EXOM with and without Markov boundary masking on four different types of SCMs. The results, measured by Effective Sample Proportion (ESP), demonstrate that injecting Markov boundary knowledge generally improves sampling efficiency and leads to better performance. The figure shows ESP values for four different scenarios (SIMPSON-NLIN, LARGEBD-NLIN, M, NAPKIN) across various density estimation models (GMM, MAF, NICE, SOSPF).

This figure illustrates the process of how the counterfactual information is used to generate parameters for the proposal distribution in the Exogenous Matching method. The input is the counterfactual event y*, which is processed by functions h and g (neural networks) to produce the masked parameters θy*. The mask m helps to incorporate the counterfactual Markov boundaries, effectively focusing the proposal distribution on the relevant parts of the exogenous distribution. Different colors highlight the information from different submodels used in the process.

This figure shows the relationship between the Effective Sample Proportion (ESP) and the negative log-likelihood (LL) during the training process of the Exogenous Matching (EXOM) method. Four different types of Structural Causal Models (SCMs) are used, along with four different density estimation models. The results indicate that as the LL (which is being minimized during training) improves, the ESP consistently improves across all combinations of SCMs and density estimation models. This suggests that the proposed optimization method effectively reduces the variance of the counterfactual estimator.
This figure shows the relationship between the negative log-likelihood (LL, which is the optimization objective), the effective sample proportion (ESP), and the failure rate (FR) during the training process of the Exogenous Matching (EXOM) method on the SIMPSON-NLIN dataset. The plot demonstrates that as the model learns (indicated by increasing LL), the sampling efficiency (ESP) improves while the failure rate (FR) decreases, eventually converging to a stable point. This supports the paper’s claim that EXOM is effective in learning good proposal distributions for counterfactual estimation.
This figure shows the relationship between the negative log-likelihood of the objective function (LL), effective sample proportion (ESP), and failure rate (FR) during the training process of the Exogenous Matching (EXOM) method on the SIMPSON-NLIN dataset. The x-axis represents the training iterations or epochs. The y-axis shows the values of LL, ESP, and FR. The plot demonstrates that as the model trains and the LL increases (the model fits better), the ESP increases (meaning more samples are effectively used in the estimation), while the FR decreases (meaning the method is performing well on a larger proportion of the test cases). This trend continues until the model converges, indicating a point where further training does not yield significant improvements.
This figure shows the results of an ablation study that investigated the impact of using Markov boundaries on the performance of the proposed method (EXOM). The study was conducted on four different types of structural causal models (SCMs), and the results indicate that using Markov boundaries generally improves sampling efficiency, especially when the boundaries are masked.
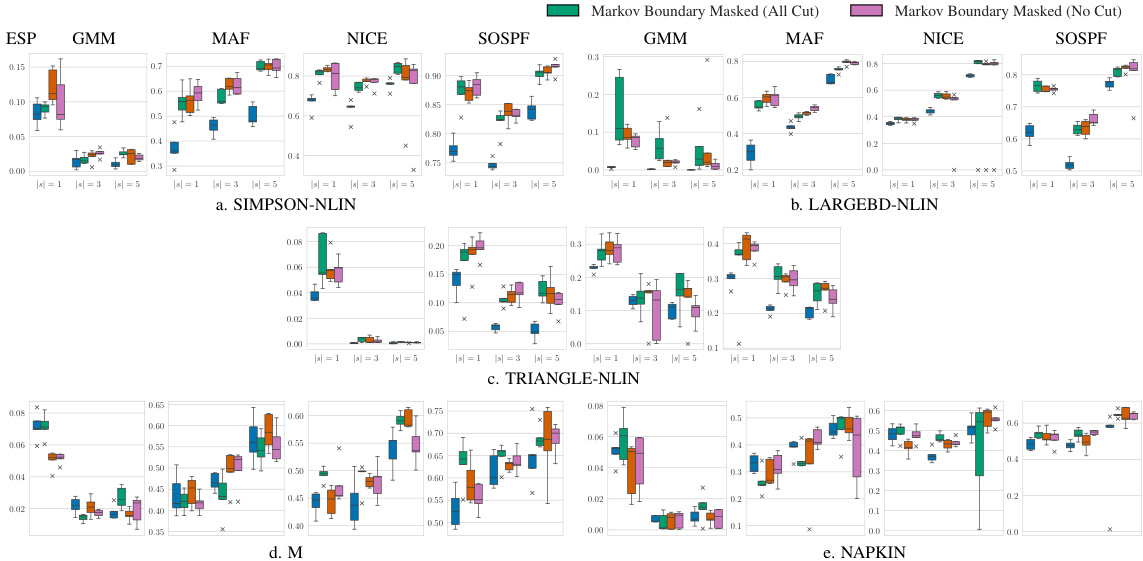
This figure presents the results of an ablation study to evaluate the impact of injecting counterfactual Markov boundaries on the performance of the proposed EXOM method. Four different structural causal models (SCMs) are tested: SIMPSON-NLIN, LARGEBD-NLIN, M, and NAPKIN. The figure shows the Effective Sample Proportion (ESP), a metric of sampling efficiency, for each SCM, comparing the EXOM performance with Markov boundaries masked to the performance without masking. The results demonstrate that in most cases, the performance with masked Markov boundaries is better.
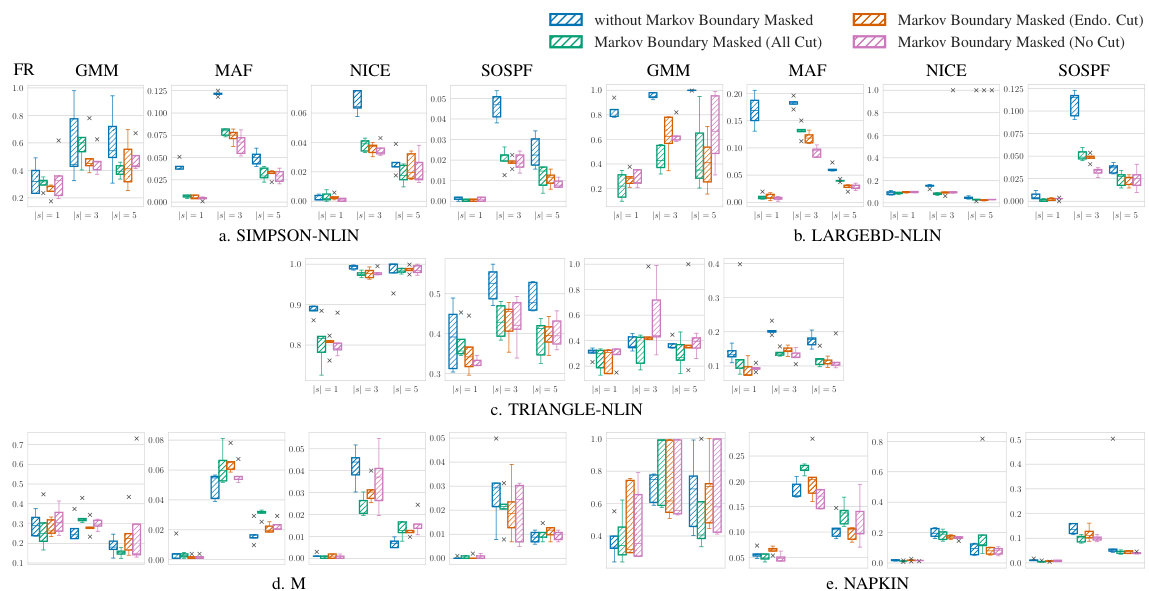
This ablation study investigates the impact of using Markov boundaries on the efficiency of the proposed Exogenous Matching (EXOM) method. Four different structural causal models (SCMs) are used, representing varying complexities: SIMPSON-NLIN, LARGEBD-NLIN, M, and NAPKIN. The results are shown for each SCM, comparing the effective sample proportion (ESP) when the Markov boundaries are masked (orange bars) versus when they are not (blue bars). Higher ESP indicates better sampling efficiency. The figure demonstrates that in most cases, masking the Markov boundaries improves the performance of EXOM.
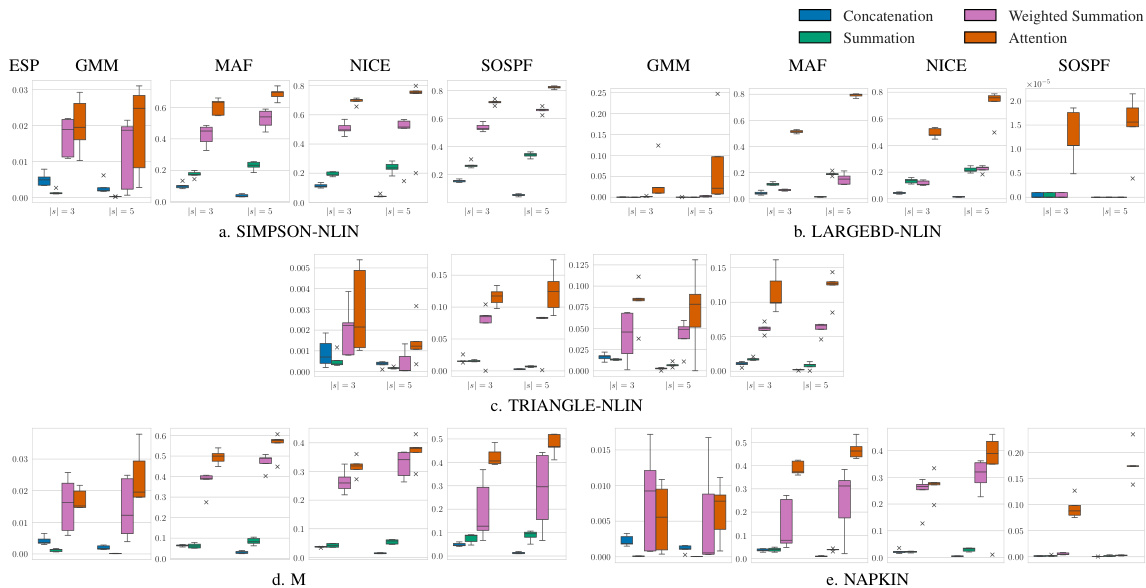
This figure presents the results of an ablation study on the impact of injecting Markov boundaries on the performance of the proposed Exogenous Matching (EXOM) method. Four different structural causal models (SCMs) are used: SIMPSON-NLIN, LARGEBD-NLIN, M, and NAPKIN, each representing a different setting. The performance metric used is Effective Sample Proportion (ESP), which measures sampling efficiency. The experiment compares the performance of EXOM with and without Markov boundaries masked. In most cases, masking the Markov boundaries leads to significantly better ESP values. This suggests that incorporating structural prior knowledge enhances the effectiveness of the EXOM method.
This figure shows the ablation study for Markov boundaries on four different settings of structural causal models (SCMs). The four SCMs are SIMPSON-NLIN, LARGEBD-NLIN, M, and NAPKIN. The ablation study focuses on the impact of Markov boundaries on the failure rate (FR), which measures how well the proposal distribution covers the state space of the counterfactual variables. Lower FR indicates that the method performs well across a broader range of counterfactual events.
More on tables

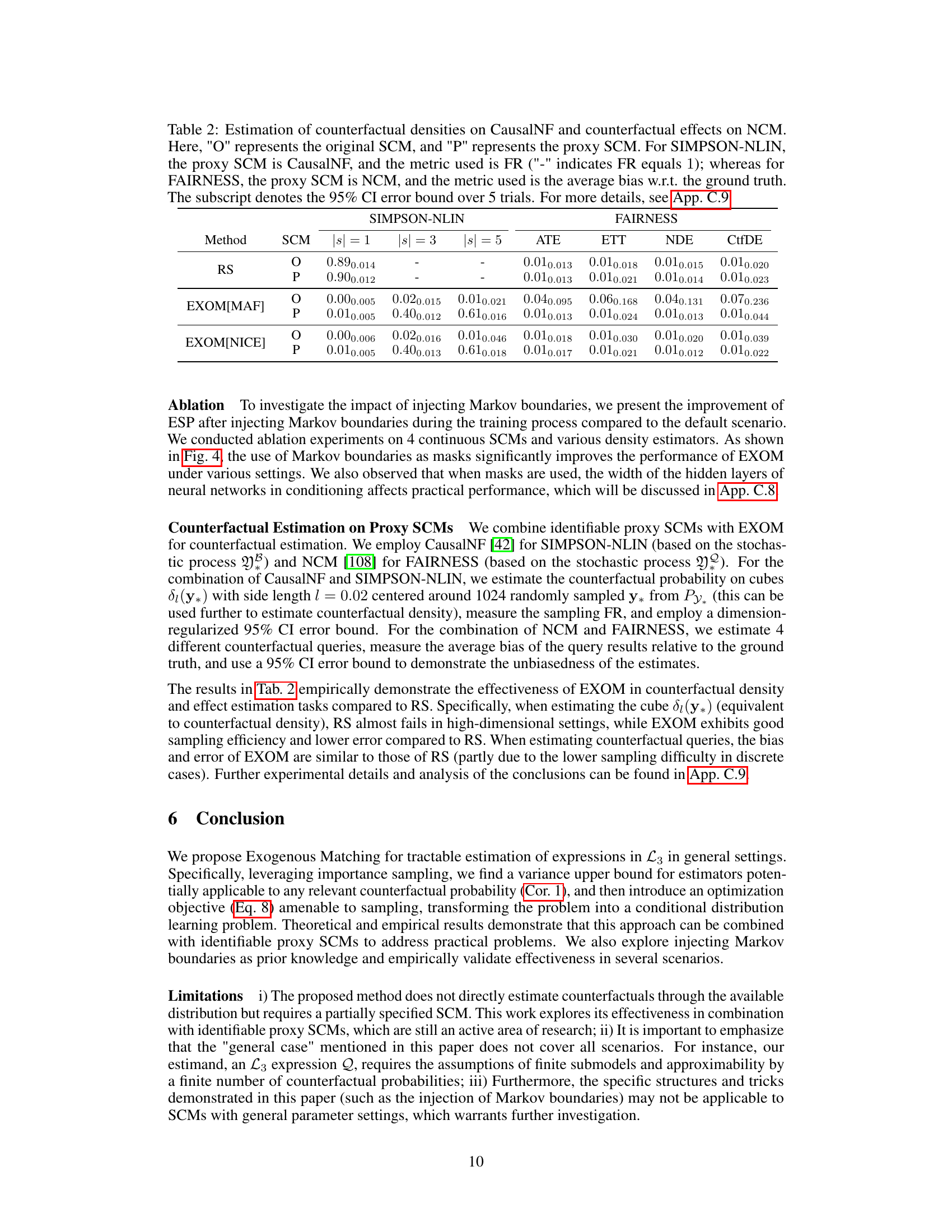
This table compares the performance of different methods (RS, EXOM[MAF], EXOM[NICE]) for estimating counterfactual densities and effects on two types of SCMs: SIMPSON-NLIN (using CausalNF as a proxy) and FAIRNESS (using NCM as a proxy). It shows the average results for different counterfactual queries (ATE, ETT, NDE, CtfDE) across various numbers of submodels (|s| = 1, 3, 5). The metrics used are FR (Failure Rate, for SIMPSON-NLIN) and average bias (for FAIRNESS), with 95% confidence intervals reported.

This table compares the performance of four different counterfactual estimation methods (Rejection Sampling, Cross-Entropy Importance Sampling, Neural Importance Sampling, and the proposed Exogenous Matching) across three different types of Structural Causal Models (SCMs) with varying numbers of submodels. The metrics used to evaluate performance are Effective Sample Proportion (ESP) and Failure Rate (FR). Higher ESP values and lower FR values indicate better performance. The SCMs represent different levels of complexity in terms of their underlying causal structures and the nature of their variables.

This table compares the performance of different methods for estimating counterfactual densities and effects on two different types of proxy SCMs: CausalNF and NCM. For SIMPSON-NLIN, it uses CausalNF as the proxy, and the failure rate (FR) is reported. For FAIRNESS, it uses NCM, reporting the average bias. Error bars (95% confidence intervals) are provided. More details can be found in Appendix C.9 of the paper.

This table compares the performance of four different counterfactual estimation methods (Rejection Sampling, Cross-Entropy based Importance Sampling, Neural Importance Sampling, and Exogenous Matching) across three different types of structural causal models (SCMs) and varying numbers of submodels (|s|). The SCMs represent different levels of complexity and assumptions. Higher ESP (Effective Sample Proportion) values indicate better sampling efficiency, while lower FR (Failure Rate) values suggest a more robust and accurate estimation.
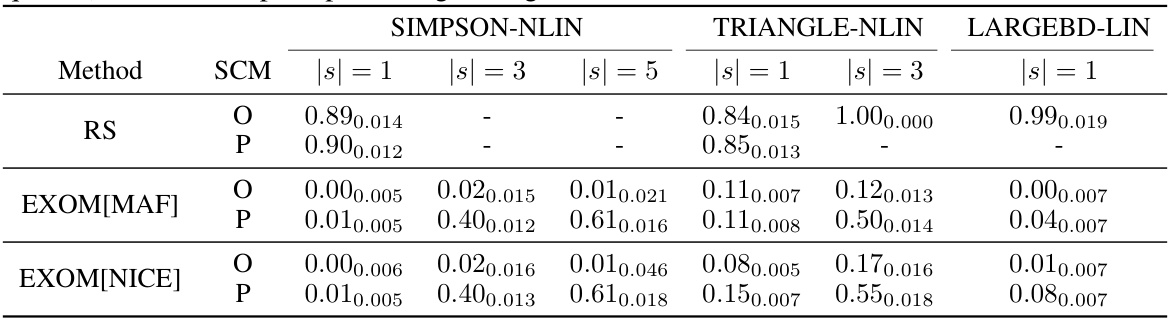
This table presents the results of counterfactual density and effect estimations using two different proxy SCMs (CausalNF and NCM). For SIMPSON-NLIN, it compares the Failure Rate (FR) of the original and proxy SCMs using different estimation methods (RS, EXOM[MAF], EXOM[NICE]). For FAIRNESS, it compares the average bias (with 95% confidence intervals) of the original and proxy SCMs for four different types of counterfactual effects (ATE, ETT, NDE, CtfDE). The results highlight the effectiveness of EXOM in both counterfactual density and effect estimations.
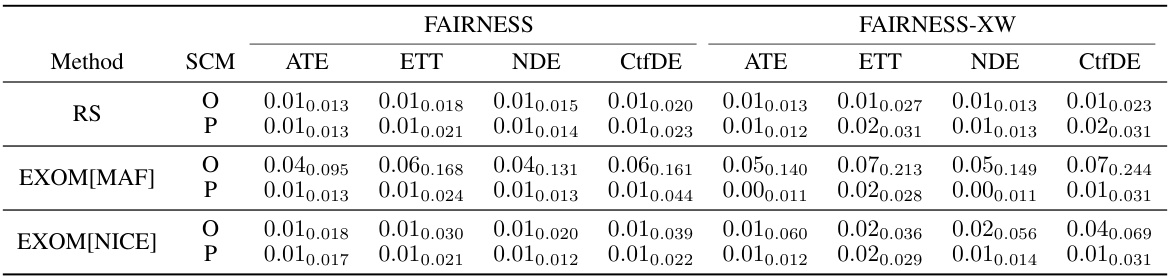
This table presents the results of counterfactual density and effect estimations using two different proxy structural causal models (SCMs): CausalNF for SIMPSON-NLIN and NCM for FAIRNESS. For SIMPSON-NLIN, the failure rate (FR) is reported, while for FAIRNESS, the average bias relative to the ground truth is shown. The results are compared against the original SCMs and rejection sampling (RS). Error bounds are included, showing the average across five runs with different random seeds. Appendix C.9 provides additional details.
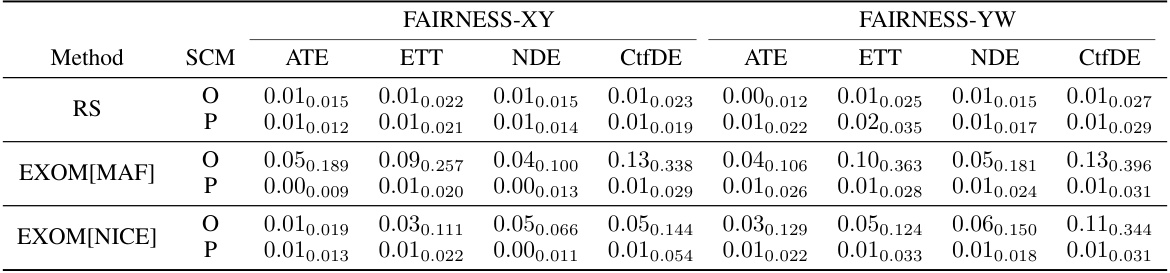
This table presents the results of counterfactual estimation experiments using two different proxy structural causal models (SCMs): CausalNF for SIMPSON-NLIN and NCM for FAIRNESS. For SIMPSON-NLIN, the failure rate (FR) is reported, indicating the proportion of samples that failed to satisfy the conditions of the counterfactual events. For FAIRNESS, the average bias of the estimations relative to the ground truth is shown, along with 95% confidence intervals. The results are separated into five different counterfactual queries (ATE, ETT, NDE, CtfDE) for fairness and different numbers of counterfactual events (|s|=1,3,5) for SIMPSON-NLIN.
Full paper#