Sample-Efficient Geometry Reconstruction from Euclidean Distances using Non-Convex Optimization

Yu7H8ZOuI2

Ipsita Ghosh et el.

TL;DR
#

Many machine learning applications rely on solving Euclidean Distance Geometry (EDG) problems, which involve reconstructing geometric configurations from pairwise distances. However, existing methods often struggle with incomplete distance information and require a large number of samples. This leads to computational limitations and reduced data efficiency, hindering their practical applicability.

This paper addresses these issues by proposing a novel algorithm called MatrixIRLS, based on iteratively reweighted least squares. This approach uses a non-convex rank minimization formulation and establishes a local convergence guarantee with a minimal number of distance samples. MatrixIRLS demonstrates improved data efficiency and scalability through numerical experiments with both simulated and real-world datasets, outperforming state-of-the-art methods. The algorithm’s ability to work with limited data and high accuracy makes it valuable across various applications.

Key Takeaways
#

Why does it matter?
#

This paper is crucial for researchers working on Euclidean Distance Geometry (EDG) problems and related areas like low-rank matrix completion. It offers a data-efficient and highly accurate algorithm, potentially impacting various fields such as molecular conformation prediction, sensor network localization, and machine learning. The novel theoretical guarantees and scalable algorithm open up exciting new avenues for future research in non-convex optimization and data-efficient machine learning.

Visual Insights
#

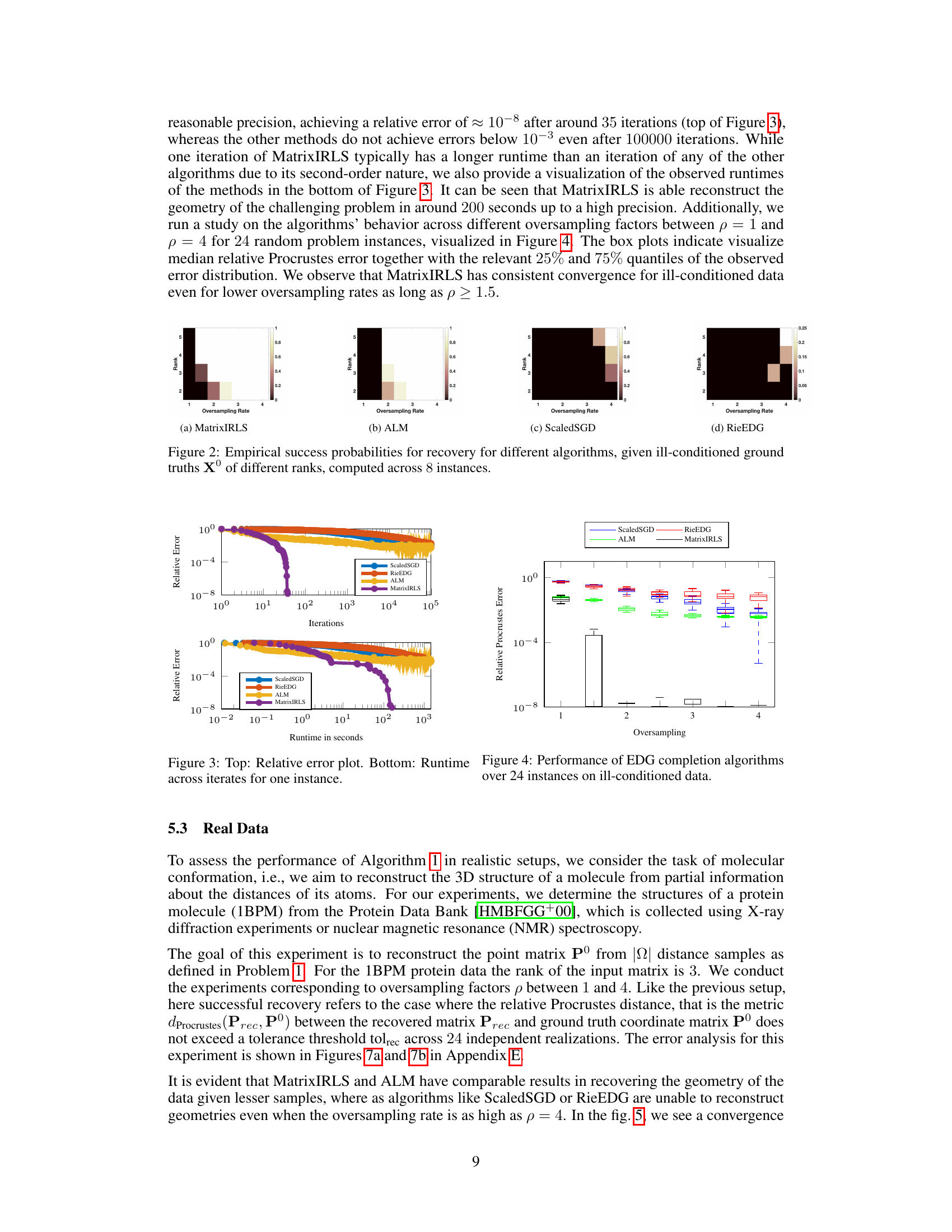
This figure displays the success rates of four different algorithms (MatrixIRLS, ALM, RieEDG, and ScaledSGD) in reconstructing the geometry of points from incomplete distance information. The success rate is plotted as a function of the ground truth rank (r) of the point configuration and the oversampling factor (p), which represents the ratio of available distances to the minimum number required. Each cell in the heatmap represents the probability of successful reconstruction across 24 independent trials. The darker the shade of beige, the higher the probability of success. This visual helps to compare the data efficiency of the four algorithms in recovering the underlying geometry under various conditions.

This table shows the execution time and relative error of the MatrixIRLS algorithm for different problem sizes (number of data points, n) when using Gaussian-distributed data. The oversampling factor p is held constant at 3. The results demonstrate the algorithm’s scalability and accuracy across various problem sizes.

In-depth insights
#

EDG Non-convexity
#

The non-convex nature of Euclidean Distance Geometry (EDG) problems presents a significant challenge in algorithmic design. Unlike convex problems with a single global minimum, EDG’s landscape is riddled with numerous local minima, hindering the ability of standard gradient-based methods to find globally optimal solutions. This non-convexity stems from the inherent difficulty of embedding points in Euclidean space based solely on incomplete distance information. Rank minimization formulations, frequently used to address the EDG problem, directly contribute to this non-convexity due to the non-convexity of the rank function itself. Iteratively Reweighted Least Squares (IRLS) methods offer a potential avenue for tackling this challenge by iteratively minimizing a sequence of weighted least-squares problems, effectively smoothing the non-convex landscape. However, theoretical guarantees for IRLS in the EDG context are often limited, typically focusing on local convergence rather than global optimality. The paper explores this challenge through a novel IRLS approach, providing a theoretical analysis that establishes local convergence under specific conditions including a restricted isometry property applied to a tangent space. This strategy offers a balance between efficient computation and rigorous theoretical backing, providing a substantial step towards better understanding and solving EDG problems within their inherent non-convexity.

MatrixIRLS Method
#

The MatrixIRLS method, a novel algorithm for Euclidean Distance Geometry (EDG) reconstruction, presents a compelling approach to address the challenges of sample efficiency and non-convexity inherent in EDG problems. It leverages an iteratively reweighted least squares (IRLS) framework, minimizing a sequence of smoothed log-det objectives. This iterative refinement process is key to its efficiency in handling the non-convex optimization landscape, and by incorporating a smoothing technique, it addresses the non-smooth nature of the problem. A major strength lies in its theoretical guarantees regarding local convergence with quadratic rate, achieved under suitable sample complexity conditions. The restricted isometry property (RIP) analysis, limited to the tangent space of a manifold, is a key element of this theoretical foundation and potentially generalizable to other non-convex approaches. The algorithm’s robustness to ill-conditioned data, as demonstrated by numerical experiments, is a significant practical advantage. Ultimately, MatrixIRLS presents a notable contribution to EDG, offering both strong theoretical foundations and excellent empirical performance, especially in data-scarce scenarios.

RIP Tangent Space
#

The concept of “RIP Tangent Space” in the context of Euclidean Distance Geometry (EDG) problems likely refers to a restricted isometry property (RIP) analysis tailored to the specific geometric structure of the problem. In EDG, we aim to recover point coordinates from a subset of pairwise distances. The solution space is a manifold, and a tangent space approximates the local geometry near a known point (e.g., a good initial guess). A standard RIP guarantees that random linear measurements preserve distances between points in a high-dimensional space. However, the RIP analysis for EDG needs to consider the non-linearity and curvature of the manifold, focusing on the tangent space to obtain a local RIP guarantee. This adaptation is crucial because standard RIP results don’t directly apply to manifolds. The analysis would likely involve demonstrating that, under certain sampling conditions (number of distances, distance distribution, etc.), linear measurements in the tangent space approximately preserve pairwise distances between points on the manifold. This would provide a foundation for the convergence analysis of algorithms that locally approximate the manifold with its tangent space, for example Iteratively Reweighted Least Squares (IRLS) methods. The sample complexity (minimum number of distances) required for the RIP to hold would be a key result of this analysis, influencing algorithm performance and data efficiency.

Data Efficiency
#

The concept of ‘data efficiency’ in the context of Euclidean Distance Geometry (EDG) problem is crucial. The paper highlights that existing convex relaxation methods are not data-efficient, requiring significantly more distance samples than necessary for accurate geometry reconstruction. The proposed MatrixIRLS algorithm addresses this limitation by leveraging a non-convex approach and achieves superior data efficiency. This is demonstrated through both theoretical analysis, establishing a local convergence guarantee with a sample complexity bound that matches the information-theoretic lower bound for low-rank matrix completion, and extensive empirical evaluations on synthetic and real-world datasets. The results showcase the algorithm’s ability to reconstruct accurate geometries from substantially fewer distance samples than state-of-the-art methods, confirming its enhanced data efficiency and robustness to ill-conditioned data. This improved data efficiency translates into reduced computational cost and increased feasibility for applications involving limited or noisy distance measurements, significantly expanding the practical utility of EDG for diverse real-world scenarios. The theoretical underpinnings coupled with the experimental validation firmly establish the algorithm’s enhanced sample efficiency, making it a significant advancement in EDG problem solving.

Future of EDG
#

The future of Euclidean Distance Geometry (EDG) appears bright, driven by its capacity to solve challenging problems across diverse fields. Further advancements in non-convex optimization techniques are crucial, promising more efficient and robust algorithms capable of handling incomplete and noisy distance data. Developing theoretical guarantees for these non-convex methods will be essential, ensuring reliable performance and predictable behavior. Exploring the interplay of EDG with machine learning, particularly in applications like protein structure prediction and sensor network localization, is key. Integration with other geometric methods and dimensionality reduction techniques could lead to even more powerful tools for data analysis and geometric inference. Finally, the development of efficient software libraries and standardized benchmarks would significantly expand the accessibility and impact of EDG.

More visual insights
#

More on figures

This figure shows the success rates of four different algorithms (MatrixIRLS, ALM, RieEDG, and ScaledSGD) in reconstructing the ground truth geometry from incomplete Euclidean distance information. The success rate is shown as a heatmap for various ranks (2-5) and oversampling factors (1-4). Each cell represents the probability of successful reconstruction across 24 independent instances. The color intensity indicates the probability of success, with darker colors representing higher probabilities. This figure highlights the data efficiency of MatrixIRLS and ALM compared to RieEDG and ScaledSGD.

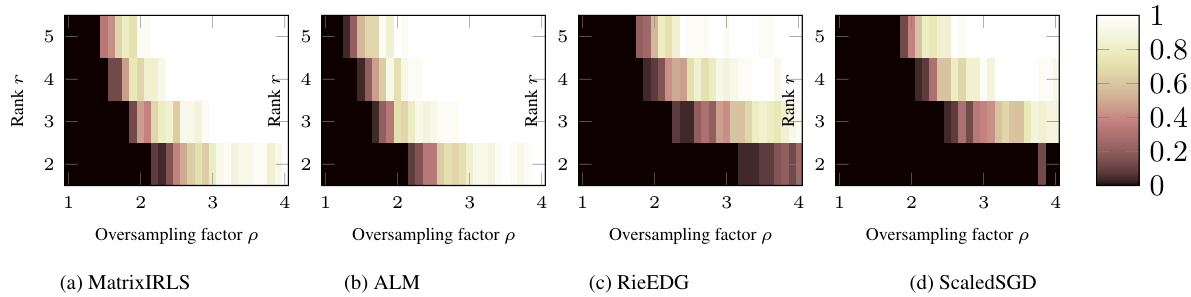
This figure shows the relative error and runtime of four different algorithms (MatrixIRLS, ALM, RieEDG, ScaledSGD) for solving the Euclidean Distance Geometry problem on an ill-conditioned dataset. The top panel displays the relative error over iterations, demonstrating the faster convergence of MatrixIRLS compared to other methods. The bottom panel shows the runtime in seconds, illustrating that MatrixIRLS achieves high precision with a reasonable runtime compared to other methods. The figure highlights MatrixIRLS’s efficiency in solving challenging instances of EDG problems.

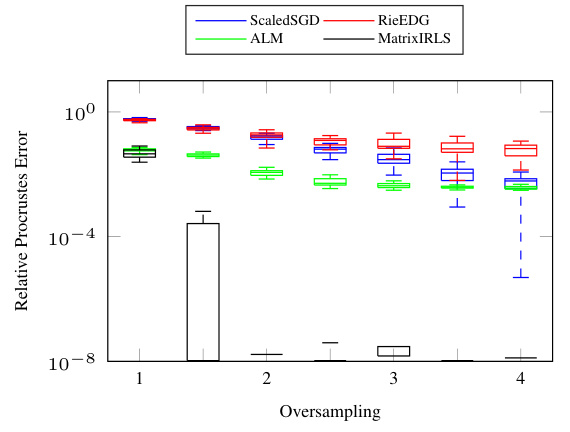
This figure shows the performance of four different algorithms (MatrixIRLS, ALM, RieEDG, and ScaledSGD) for solving the Euclidean Distance Geometry (EDG) problem on ill-conditioned data. The box plots illustrate the median relative Procrustes error, along with the 25th and 75th percentiles, across 24 different problem instances for various oversampling factors (1, 1.5, 2, 2.5, 3, 3.5, 4). The results demonstrate the robustness of MatrixIRLS in handling ill-conditioned data, showing consistent convergence even at lower oversampling rates.

This figure shows a 3D reconstruction of the protein 1BPM molecule using the MatrixIRLS algorithm. Only 0.5% of the pairwise distance samples were used for the reconstruction. The reconstruction is shown in blue, and the ground truth structure is shown in pink. The high accuracy of the reconstruction even with a very limited amount of data demonstrates the efficiency of the proposed algorithm.

This figure shows the success rate of four different algorithms (MatrixIRLS, ALM, RieEDG, and ScaledSGD) in reconstructing the ground truth geometry from a subset of pairwise Euclidean distances. The success rate is plotted against the oversampling factor (p) for different ranks (r) of the ground truth Gram matrix. Each point represents the average success rate over 24 different problem instances. The figure demonstrates the data efficiency of MatrixIRLS and ALM compared to RieEDG and ScaledSGD.

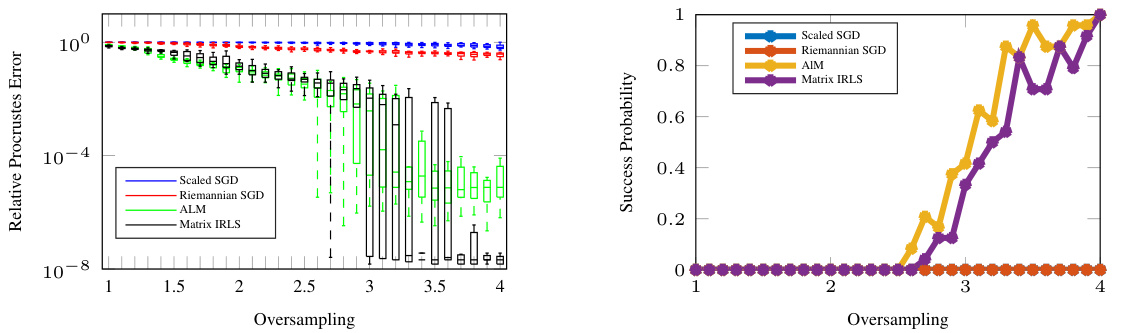
This figure displays the success rates of four different algorithms (MatrixIRLS, ALM, RieEDG, and ScaledSGD) in reconstructing the ground truth geometry from incomplete distance measurements. The success rate is plotted against the oversampling factor (p) for various ranks (r) of the underlying geometry. Each point represents the probability of successful reconstruction averaged over 24 independent trials. The figure demonstrates the relative performance of the algorithms with respect to data efficiency.

This figure visualizes the reconstruction of the US cities data using the MatrixIRLS algorithm with different oversampling factors (1.5, 2.5, and 3.5). Each subplot shows the geographic locations of the cities as reconstructed by the algorithm. The degree to which the reconstruction matches the actual geographic distribution of the cities indicates the algorithm’s accuracy at different sampling rates. Higher oversampling factors generally lead to more accurate reconstructions.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

EDG Non-convexity#

MatrixIRLS Method#

RIP Tangent Space#

Data Efficiency#

Future of EDG#

More visual insights#

Full paper#