Learning Bregman Divergences with Application to Robustness

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it introduces a novel method for learning Bregman divergences, a powerful tool for measuring semantic similarity in high-dimensional data. This has significant implications for robust machine learning, particularly in improving the robustness of models against real-world image corruptions. The work opens new avenues for adversarial training techniques and advances the field of metric learning. The proposed method’s superior performance on benchmark datasets highlights its potential for broader applications in computer vision and beyond.

Visual Insights

#

This figure shows a comparison of L2 distance and learned Bregman divergence in a 2D space. (a) shows training samples with original point at (0,0), noisy points in blue, and corrupted points in red. (b) shows the heatmap of L2 distance, failing to distinguish between noisy and corrupted points. (c) shows the heatmap of learned Bregman divergence, successfully distinguishing between noisy and corrupted points.

This table summarizes the notation and concepts used in the paper, focusing on Bregman Divergences (BD) and mirror descent. It compares the generic concepts with specific examples such as the Euclidean norm and KL divergence. The last column highlights how the authors’ proposed learned BDs differ from and extend previous work, specifically in their application to robustness.

In-depth insights

#

Bregman Divergence

#

Bregman Divergence (BD) is a powerful generalization of several common distance measures, offering a flexible framework for measuring dissimilarity in various spaces. The core idea behind BD is its reliance on a strongly convex function, the base function, to define the distance between two points. This allows for the incorporation of underlying geometric structures inherent in the data space which are often ignored by standard Euclidean metrics. The authors leverage BD to learn semantic similarity between images, going beyond simple pixel-wise differences. This is achieved through a self-supervised learning algorithm that learns a suitable base function, making the resulting BD sensitive to meaningful image corruptions. This learned BD then forms the foundation for the development of adversarial attacks, replacing standard gradient descent with mirror descent. This innovative approach significantly enhances the robustness of adversarially trained models, particularly for contrast corruptions. The ability to learn BD from data, coupled with its elegant mathematical properties, makes it a promising tool for various computer vision tasks requiring robust similarity assessment.

Adversarial Training

#

Adversarial training is a crucial technique in machine learning for enhancing model robustness against adversarial attacks. The core idea is to augment the training data with adversarially perturbed examples, generated by methods such as Projected Gradient Descent (PGD), to explicitly expose the model to inputs designed to fool it. This process forces the model to learn more robust features, less susceptible to minor input modifications. The effectiveness of adversarial training hinges on several factors: the choice of attack algorithm, the strength of the attack (perturbation size), and the training strategy employed. While highly effective in improving robustness, adversarial training also presents challenges. It can be computationally expensive, requiring significant resources for generating adversarial samples and retraining models. It can also lead to a trade-off between robustness and standard accuracy, where models may perform less well on clean, unperturbed data after undergoing adversarial training. Ongoing research focuses on improving the efficiency and efficacy of adversarial training, exploring alternative attack strategies, and mitigating the potential downsides of the technique.

Corruption Robustness

#

The research explores image corruption robustness, focusing on learning Bregman divergences to measure semantic similarity. Unlike traditional L_p norms, learned divergences prioritize semantic similarity, considering real-world corruptions (blur, contrast changes) as close to the original, even if pixel-wise differences are large. This is achieved through a novel self-supervised algorithm, learning base functions for Bregman divergences from image data. The learned divergence effectively distinguishes between corrupted and noisy images, exceeding human perceptual similarity judgments on relevant datasets. Moreover, it improves adversarial training (AT) by replacing projected gradient descent with mirror descent, leading to state-of-the-art robustness against contrast and fog corruptions, significantly surpassing L_p and LPIPS-based AT methods. The approach demonstrates the power of learning data-driven similarity measures for robust machine learning, showcasing its potential for addressing the challenges of out-of-distribution generalization.

Mirror Descent

#

Mirror descent is a powerful optimization algorithm particularly well-suited for problems involving non-Euclidean geometries or complex constraint sets. Its key advantage lies in its ability to adapt to the underlying geometry of the problem space, using a Bregman divergence to measure distances and guide the search for optimal solutions. Unlike gradient descent, which relies on Euclidean distances, mirror descent employs a more general distance metric defined by the chosen Bregman divergence. This adaptability is crucial when dealing with data that is not well-represented in a Euclidean setting, such as probability distributions or other complex structures. The algorithm elegantly integrates a mirror map that transforms the original space into a dual space where the optimization is simpler and often more efficient. The method’s efficiency stems from its ability to handle constraints in a natural way, through projections onto the feasible set in the primal space. In the context of adversarial training, mirror descent offers a compelling alternative to standard gradient-based attacks, by utilizing learned Bregman divergences to define neighborhoods of clean images and perform attacks in a semantically meaningful way. This leads to improved robustness against real-world corruptions, as demonstrated by the paper’s results on CIFAR-10-C. However, challenges remain, notably the computational cost and the heuristic nature of projection methods involved; future work should focus on improving efficiency and the development of more sophisticated projection techniques.

Semantic Similarity

#

The concept of semantic similarity is central to this research, focusing on how to effectively measure the similarity between images based on their meaning rather than simply their pixel-level differences. The authors critique existing methods like L_p distances, arguing that they fail to capture true semantic meaning. Their proposed solution is to learn Bregman divergences directly from the data, resulting in a more flexible and robust metric. This learned divergence is then used to refine adversarial training, resulting in improved image robustness to various corruptions. The innovation lies in learning a task-specific distance metric instead of relying on pre-defined Euclidean or other fixed-distance functions. This focus on semantic similarity allows for a more nuanced understanding of image relationships and a more effective approach to improving the robustness of image recognition models.

More visual insights

#

More on figures

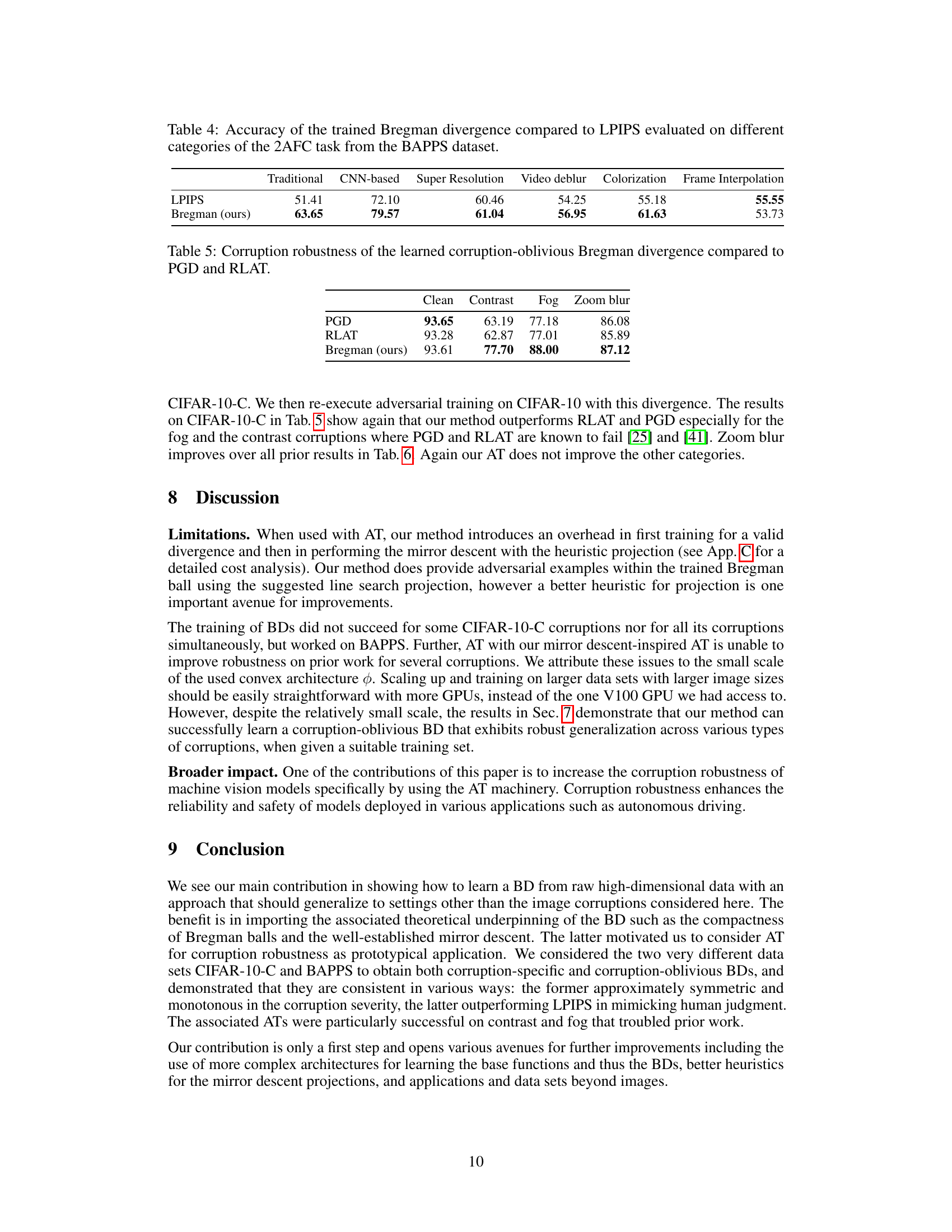
This figure compares the distributions of Euclidean distances and learned Bregman divergences between noisy images and contrast-corrupted images with respect to clean images. The left panel (a) shows that both noisy and corrupted images have a similar distribution of Euclidean distances to the clean images. The right panel (b) demonstrates that the learned Bregman divergence effectively distinguishes between noisy and corrupted images, showing that corrupted images are significantly closer to the clean image than noisy images are according to the learned Bregman divergence.

This figure illustrates the concept of learning a Bregman Divergence (BD) in a simplified 2D space. It compares the L2 distance (Euclidean distance) and the learned BD in distinguishing between noisy and corrupted data points. The L2 distance fails to differentiate between noisy and corrupted points, while the learned BD successfully identifies corrupted points as closer to the original point than noisy points, showcasing its effectiveness in measuring semantic similarity.

This figure illustrates the concept of learning a Bregman Divergence (BD) in a 2D space. Panel (a) shows training samples: the origin (clean image), noisy points (blue), and corrupted points (red). Panel (b) displays the heatmap of the L2-distance from the origin, demonstrating its inability to differentiate between noisy and corrupted data points. Finally, panel (c) presents the heatmap of the learned BD, highlighting its superior performance in distinguishing corrupted from noisy samples by placing corrupted points closer to the origin than noisy points.

This figure illustrates the difference between the learned Bregman Divergence and the standard L2 distance. In 2D space, the original point is (0,0), noisy points are shown in blue, and corrupted points are shown in red. The L2 distance heat map shows the inability to distinguish between noisy and corrupted points, whereas the learned BD heatmap correctly identifies corrupted points as much closer to the origin than noisy points.

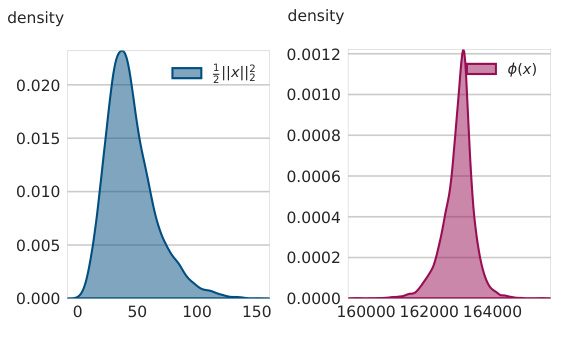
This figure demonstrates the performance of the learned Bregman divergence on higher-dimensional images (256x256) from the ImageNet dataset. It shows that even though the Bregman divergence was trained on lower-resolution images (32x32) from CIFAR-10, it is able to effectively distinguish corrupted images from noisy images, highlighting the generalizability of the learned divergence.

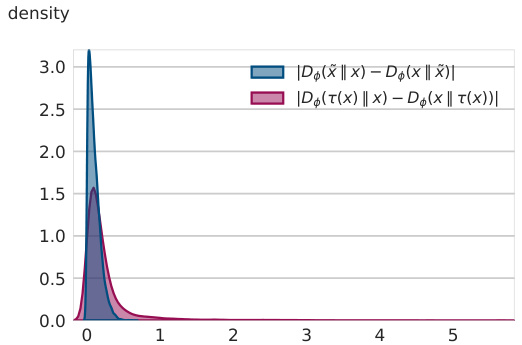
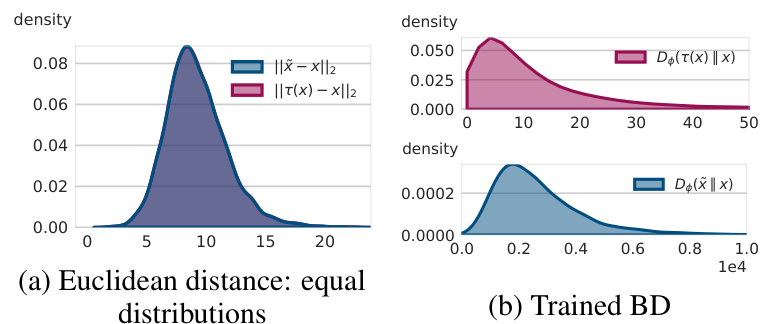
This figure shows the distribution of the absolute differences between D(x’ || x) and D(x || x’) (blue) and D(τ(x) || x) and D(x || τ(x)) (red) for 10,000 images in the test set. It demonstrates that the learned Bregman divergence is not perfectly symmetric, but the asymmetry is relatively small. This is important to note, as a perfectly symmetric Bregman divergence is simply a quadratic function, which limits its expressiveness.

This figure shows the performance of the learned Bregman divergence on higher-dimensional images (256x256) from the ImageNet dataset. It demonstrates the ability of the Bregman divergence to distinguish between corrupted and noisy images even though the model was trained on lower-resolution (32x32) CIFAR-10 images.

This figure shows the performance of the learned Bregman divergence on higher-dimensional images (256x256) from the ImageNet dataset. It demonstrates the ability of the Bregman divergence to distinguish between corrupted and noisy images even though the model was trained on lower-resolution (32x32) CIFAR-10 images. Each row represents a different image, showing the original, corrupted, and various noisy versions.

More on tables

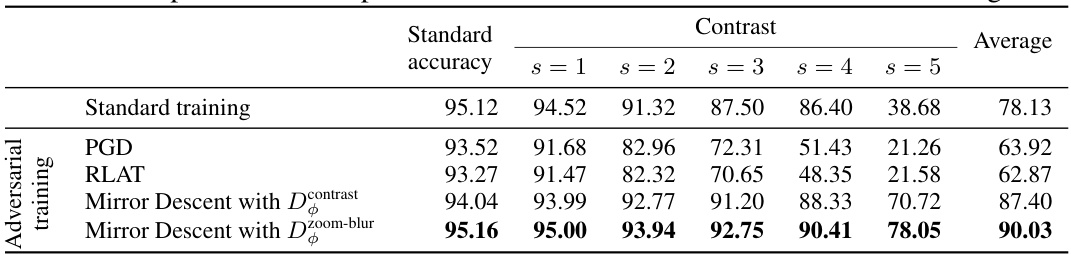
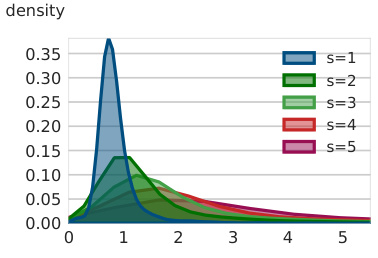
This table compares the corruption robustness of models trained using different methods: standard training, Projected Gradient Descent (PGD), Relaxed LPIPS Adversarial Training (RLAT), and Mirror Descent with two different learned Bregman divergences (Dcontrast and Dzoom-blur). Robustness is measured across five severity levels (s=1 to s=5) for contrast corruption, and an average robustness is also reported. The results demonstrate the superior performance of the proposed Mirror Descent method, especially at higher severity levels, in contrast to the commonly used PGD and RLAT techniques.

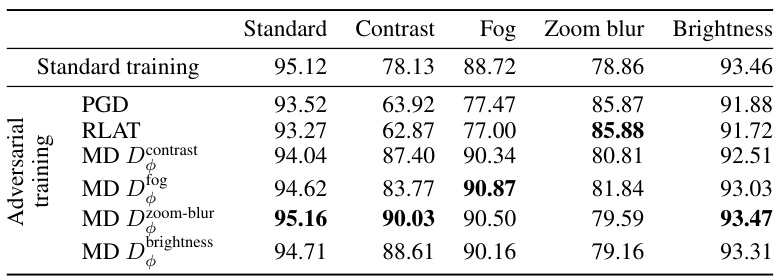
This table compares the corruption robustness of a standard-trained model against models trained using three different adversarial training methods: Projected Gradient Descent (PGD) with L2 norm, Relaxed LPIPS Adversarial Training (RLAT), and Mirror Descent with the learned Bregman divergence. The robustness is evaluated across several common image corruptions (contrast, fog, zoom blur, brightness) using the CIFAR-10-C dataset, and measured by the average accuracy across different corruption severities.

This table compares the accuracy of the learned Bregman divergence and LPIPS on the Berkeley-Adobe Perceptual Patch Similarity (BAPPS) dataset. The BAPPS dataset contains image triplets with human judgments on which distortion is more similar to the original. The table shows the accuracy for each of the six categories of the 2AFC (two-alternative forced choice) test in the BAPPS dataset. The comparison demonstrates the performance of the learned Bregman divergence against a state-of-the-art method for perceptual similarity.

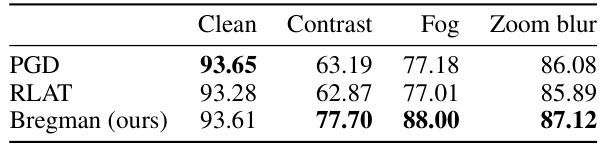
This table shows the corruption robustness results for different models on the CIFAR-10-C dataset. It compares the performance of the proposed corruption-oblivious Bregman divergence approach against the standard Projected Gradient Descent (PGD) and Relaxed LPIPS Adversarial Training (RLAT) methods. The results are presented for four common image corruptions: clean, contrast, fog, and zoom blur. The accuracy values show how well each model generalizes when faced with different corruption levels.

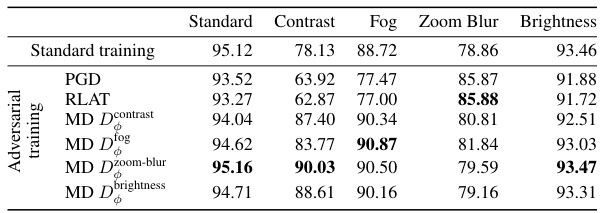
This table compares the corruption robustness of a standard-trained model against models trained using three different adversarial training methods: Projected Gradient Descent (PGD) with L2 norm, Relaxed LPIPS Adversarial Training (RLAT), and Mirror Descent with the learned Bregman divergence. The robustness is evaluated across five types of image corruptions (contrast, fog, zoom blur, brightness, and others) at various severities. The table shows the accuracy of each method on each corruption type, highlighting the superior performance of Mirror Descent with the learned Bregman divergence, particularly in handling contrast and fog corruptions.

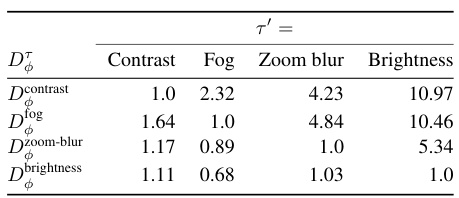
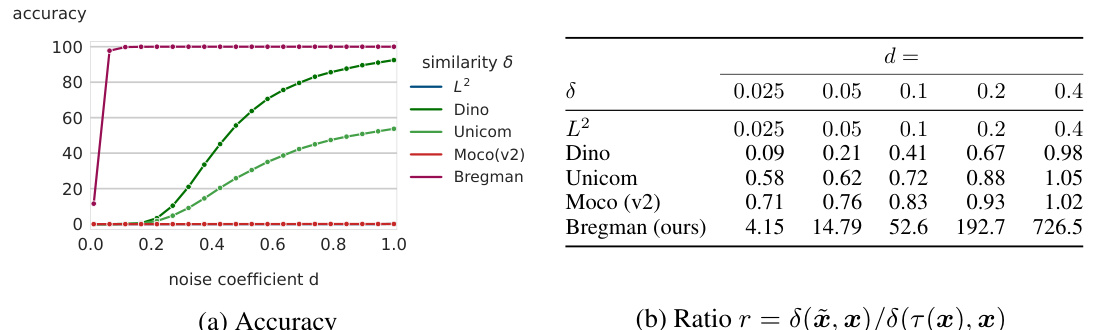
This table presents the results of evaluating the cross-corruption generalization of learned Bregman divergences. It shows the ratio of the learned Bregman divergence for a given corruption τ’ to the Bregman divergence for its training corruption τ, averaged over the test set. This assesses how well a divergence trained for one corruption generalizes to other corruptions.

Full paper

#