Randomized Strategic Facility Location with Predictions

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in mechanism design and facility location. It significantly advances our understanding of learning-augmented mechanisms, particularly by demonstrating the power of randomization. The work also provides tight theoretical bounds, guiding future research on achieving better approximations in both single and multi-dimensional settings, paving the way for more efficient and effective facility location strategies in various applications.

Visual Insights

#

This figure illustrates the geometric relationships between the centroid (G), orthocenter (H), and circumcenter (O) of a triangle formed by three points (xe1, xe2, xe3). It highlights that these three points are collinear, forming the Euler line, and the distance from the centroid to the circumcenter is half the distance from the centroid to the orthocenter. The figure also shows the medians, altitudes, and perpendicular bisectors of the triangle.

In-depth insights

#

Rand. Facility Loc.

#

The heading ‘Rand. Facility Loc.’ likely refers to randomized facility location problems. This area of research focuses on finding the optimal location for a new facility, considering that the agents involved might strategically misreport their locations to influence the placement in their favor. A core challenge is designing truthful mechanisms, ensuring agents cannot benefit from lying. The introduction of randomization adds complexity, but also the potential for improved solutions, particularly when coupled with machine-learned predictions regarding agents’ true preferences or optimal facility location. Randomization can help mitigate strategic manipulation, broadening the scope of effective truthful mechanisms beyond the limitations of deterministic approaches. The research likely explores the trade-offs between the robustness (worst-case performance) and the consistency (performance with accurate predictions) of randomized mechanisms, seeking to understand the conditions under which randomization significantly improves the approximation of the optimal social cost. Key aspects of the research likely involve theoretical analysis, providing bounds on achievable performance, and potentially experimental evaluations to validate the theoretical findings and to assess the practical implications of employing different types of predictions.

Truthful Learn. Mech.

#

The heading ‘Truthful Learn. Mech.’ suggests a focus on mechanisms that incentivize truthful behavior in a learning-augmented setting. This implies the design of systems that combine the principles of mechanism design, specifically focusing on truthfulness, with machine learning. Truthfulness ensures that participants gain no advantage by providing false information. The addition of learning suggests the use of predictions or learned models to improve the mechanism’s efficiency and/or fairness. A key challenge would be to balance the benefits of learning (improved performance) with the need to maintain truthfulness, which is often at odds with optimizing for accuracy. The research likely explores the trade-offs between these two goals and aims to design mechanisms robust against manipulation and benefitting from predictions, even if those predictions are imperfect. This is a crucial area of research that could have significant real-world implications.

Single-Dim. Results

#

The single-dimensional analysis reveals crucial insights into the strategic facility location problem. A key finding is the Pareto optimality of two existing mechanisms: a deterministic mechanism achieving perfect consistency (1) and a robustness of 2, and a randomized mechanism with both consistency and robustness of 1.5. This highlights the inherent trade-off between these two desirable properties. The lower bound analysis rigorously demonstrates that for any randomized truthful mechanism, improvements in consistency inevitably lead to reductions in robustness and vice-versa, even with the strongest prediction available. This trade-off is completely characterized, showing the optimality of the previously mentioned mechanisms. The results showcase the limitations of deterministic approaches and the value of randomization, but also reveal that even the most powerful predictions cannot overcome the fundamental conflict between consistency and robustness in the single-dimensional setting.

Two-Dim. Analysis

#

In a two-dimensional analysis of strategic facility location, the complexities increase significantly compared to the single-dimensional case. Randomized mechanisms, while offering potential advantages in mitigating strategic behavior, present new challenges in analysis and design. The optimal facility location in two dimensions is no longer simply a median but rather a point that balances distances in a plane. This necessitates new techniques to determine lower bounds and evaluate the effectiveness of prediction incorporation. Tight bounds for the approximation of the optimal egalitarian social cost become harder to establish and the effect of prediction types on robustness and consistency requires careful examination. The interaction between agent strategies and the facility placement algorithm in two dimensions is significantly richer, impacting the design of truthful mechanisms. The analysis must address the potential for agents to manipulate their reported locations to influence facility placement in their favor, requiring robust techniques to handle such strategic behavior and explore the impact of stronger predictions on the Pareto frontier of mechanism performance.

Future Research

#

The paper’s exploration of randomized strategic facility location with predictions opens several avenues for future work. Extending the theoretical analysis to higher dimensions beyond the single-dimensional and two-dimensional cases studied would be valuable. The current lower bounds for approximation ratios in these higher dimensions are less tight than those in the lower dimensions, offering a rich area for investigation. The work’s focus on egalitarian social cost suggests a natural extension to explore other social cost functions such as utilitarian cost, leading to different trade-offs between robustness, consistency, and approximation. Furthermore, the impact of different types of predictions is significant, with stronger predictions generally leading to improved performance; a more in-depth comparison of prediction types and their value across various settings is needed. Finally, while the paper incorporates machine-learned predictions, investigating alternative prediction methods beyond the ones explored, including approaches that are more robust to noisy or adversarial data, could strengthen the results and enhance the practical relevance of the learning-augmented framework. Developing algorithms that can robustly leverage different types of predictions while maintaining truthfulness and optimizing various social cost functions would be crucial for deployment in real-world applications.

More visual insights

#

More on figures

This figure illustrates the transformation of an arbitrary mechanism into an ONLYM mechanism in the proof of Lemma 1. The top part shows an arbitrary mechanism, highlighting the probability distribution of its output. The bottom part displays the equivalent ONLYM mechanism, concentrating the probability mass at the endpoints (XL, XR) and the midpoint M. The probabilities are adjusted using coefficients qe and qr based on the expected locations πe and πr of the original mechanism, ensuring the resulting ONLYM mechanism has the same consistency and robustness properties as the original one.

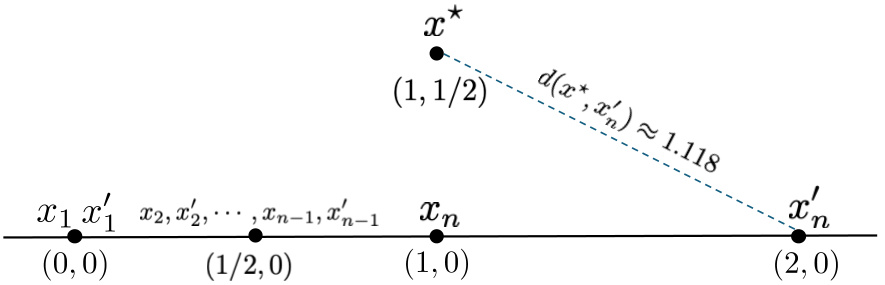
This figure is used in the proof of Theorem 2 in Section 4.1: Impossibility Results. It illustrates two instances, x and x’, on a line. Instance x has agents located at (0,0), (1/2,0), and (1,0). Instance x’ is identical except the last agent is at (2,0). The point x* represents the optimal location for instance x’ with minimum cost under the constraint that the distance between x* and xn is at least 1/2.

Full paper

#