↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Data-driven algorithm design helps select optimal algorithm parameters, but existing methods struggle with computational efficiency, especially for problems with many parameters. The ‘dual’ loss function often has a piecewise-decomposable structure – well-behaved except for sharp transitions – making efficient learning difficult. Prior work primarily focused on sample efficiency, leaving computational efficiency largely unaddressed.
This paper tackles the computational efficiency challenge by proposing output-sensitive techniques. It uses computational geometry to efficiently enumerate pieces of the dual loss function, drastically reducing computation compared to worst-case bounds. This approach, combined with execution graphs visualizing algorithm states, leads to significant speedups in learning algorithm parameters for clustering, sequence alignment, and pricing problems, demonstrating the practical benefits of output-sensitive ERM.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in algorithm design and machine learning. It introduces output-sensitive techniques to accelerate ERM, a significant improvement over worst-case approaches. This work opens new avenues for efficient learning in high-dimensional parameter spaces, impacting various applications like clustering and sequence alignment.
Visual Insights#
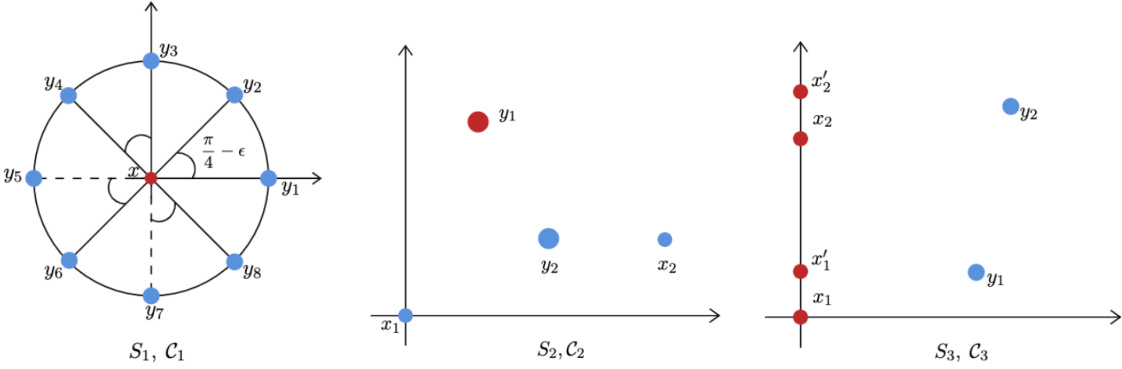
This figure shows three different clustering instances (S1, C1), (S2, C2), and (S3, C3), each with a different distribution of points and target clustering. The purpose is to demonstrate that different linkage-based clustering algorithms (single, complete, and median linkage) perform differently depending on the distribution of points, highlighting the need to interpolate or adapt the linkage procedures based on the data to optimize clustering performance.
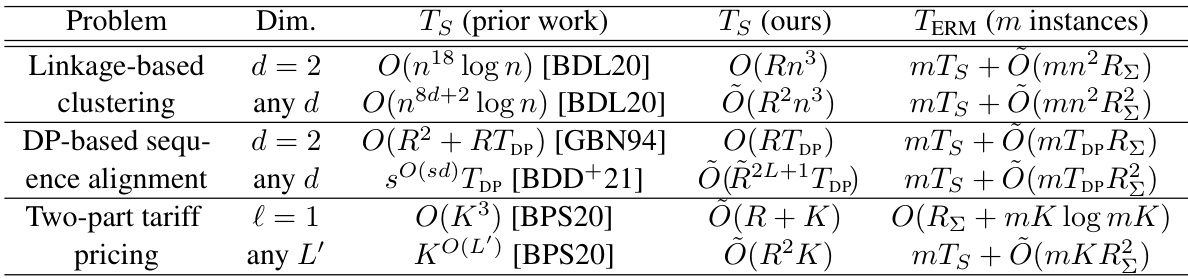
This table summarizes the running times of the proposed output-sensitive algorithms for three different data-driven algorithm design problems: linkage-based clustering, dynamic programming-based sequence alignment, and two-part tariff pricing. It compares the running times of prior work to the running times of the proposed algorithms, showing a significant improvement when the number of pieces in the dual class function is small. The table also breaks down the running time into components for computing the pieces of the sum dual loss function and enumerating the pieces on a single problem instance.
Full paper#



















