↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning studies focus on the “sample complexity”—how much data is needed to learn effectively. This paper tackles a fundamental question: Can we understand the behavior of infinite systems by only studying their finite parts? Previous research suggests this might be true in some cases, but the exact relationship hasn’t been fully clarified for supervised learning.
This paper proves that a hypothesis class is learnable if and only if all its finite subsets (projections) are learnable. This holds for various loss functions (measures of error), including common ones like squared error and cross-entropy. The results demonstrate an almost-exact compactness between transductive and PAC (Probably Approximately Correct) learning frameworks, which are important in analyzing the efficiency and accuracy of learning algorithms.
Key Takeaways#
Why does it matter?#
This paper significantly advances our understanding of supervised learning’s fundamental nature. By establishing a close relationship between the learnability of a hypothesis class and its finite projections, it provides a crucial theoretical foundation. This work impacts research by simplifying the analysis of complex learning problems, potentially leading to more efficient algorithms and improved generalization. The almost-exact compactness result bridges the gap between transductive and PAC learning, unifying distinct research areas.
Visual Insights#
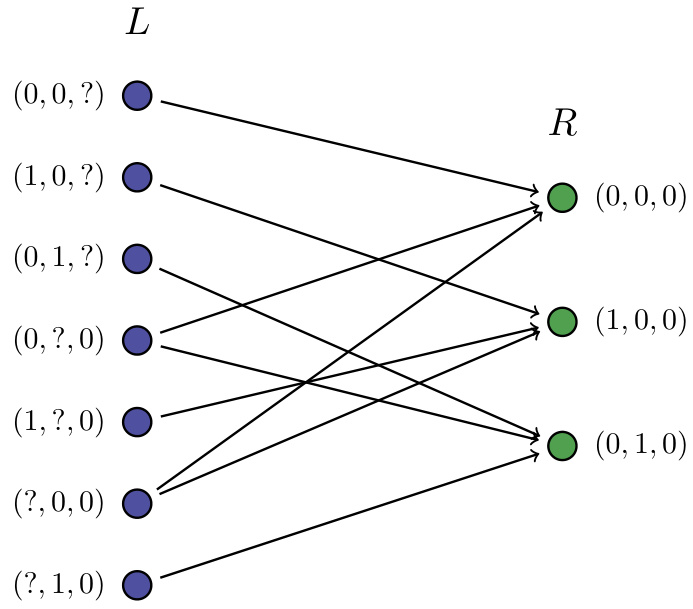
This figure shows a bipartite graph representing the variables and functions in a transductive learning model. The left side (L) represents variables that can take values in the label space Y. The right side (R) represents functions, each of which depends on a subset of the variables and outputs a value in R≥0. The edges indicate the dependencies between the variables and the functions. The example demonstrates a case with 3 unlabeled data points, leading to a specific set of possible hypothesis behaviors.
Full paper#



















