↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many applications need reliable and robust learned dynamical systems; however, existing methods lack strong global stability guarantees. This often leads to unpredictable behavior in real-world scenarios, hindering the adoption of data-driven models. The challenge lies in ensuring stability not just around training data but across the entire state space. Prior works often struggle with this issue due to limitations in expressing complex dynamics.
This paper introduces Extended Linearized Contracting Dynamics (ELCD), a novel approach that uses extended linearization and latent space transformations to guarantee global stability, equilibrium contractivity, and global contractivity. The authors prove these properties theoretically. ELCD demonstrates superior performance on high-dimensional datasets compared to prior state-of-the-art models; achieving notably better results in trajectory fitting and generalization.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces ELCD, the first neural network-based dynamical system with global contraction guarantees. This addresses a critical challenge in the field by providing strong stability and robustness guarantees for learned systems, which is crucial for safety-critical applications like robotics and autonomous systems. The work also opens up new avenues for research on learning contracting dynamics in complex spaces and metrics, and offers potential improvements to existing model training methods. These advancements are relevant to current trends in deep learning and dynamical systems, and have wide-ranging potential in applications where robust and stable system behavior is essential.
Visual Insights#

This figure compares the performance of ELCD models with and without a learned coordinate transformation. The left panel shows an ELCD model trained without a transformation; its trajectories converge quickly to the equilibrium point, reflecting the model’s inherent contractivity. The right panel displays an ELCD model that utilizes a learned transformation, and its trajectories more closely match the behavior of a vector field that is contractive with respect to a non-Euclidean metric. This highlights the importance of the coordinate transformation for capturing complex dynamics that may not fit the standard ELCD framework.
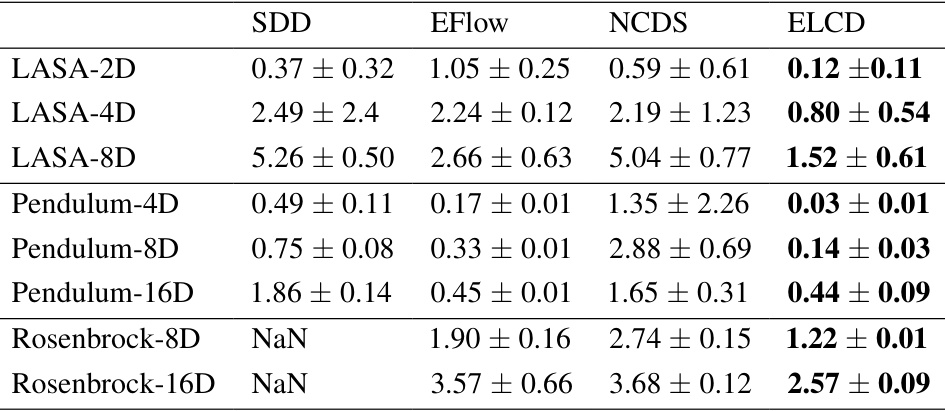
This table presents the mean dynamic time warping distance (DTWD) and standard deviation, calculated across 10 independent runs, for four different models (SDD, EFlow, NCDS, ELCD) applied to three distinct datasets (LASA, multi-link pendulum, and Rosenbrock). Lower DTWD values indicate better performance, meaning the model’s predicted trajectories more closely match the ground truth trajectories.
In-depth insights#
ELCD: Global Stability#
The heading ‘ELCD: Global Stability’ suggests a section dedicated to proving the global stability guarantees offered by the Extended Linearized Contracting Dynamics (ELCD) model. This would likely involve demonstrating that regardless of initial conditions, the system governed by ELCD will converge to a unique equilibrium point. A rigorous mathematical proof would be central, potentially leveraging Lyapunov functions or contraction theory to establish exponential stability. The discussion would likely delve into the specific conditions necessary for these guarantees to hold, such as assumptions on the neural network architecture or the properties of the learned vector field. Furthermore, it may highlight how the choice of metric influences the global stability analysis. Specific theorems and lemmas underpinning the proof would be presented, demonstrating the system’s robust behavior in the face of uncertainty and disturbances. The section would distinguish ELCD’s global stability from local or asymptotic stability found in other approaches, emphasizing the broader applicability of ELCD’s guarantees. Ultimately, this section would solidify the claims of ELCD’s reliability and predictability, a crucial aspect for deployment in real-world applications.
Latent Space Dynamics#
Utilizing latent space for dynamical systems offers a powerful approach to address the challenges of high dimensionality and complex nonlinearities present in real-world data. By mapping the original high-dimensional data into a lower-dimensional latent space via a learned transformation (like an autoencoder), the complexity of the system is reduced. This allows for learning simpler dynamics in the latent space, which can then be mapped back to the original data space. The key benefit is that the learned dynamics can capture the essence of the underlying system with fewer parameters, leading to enhanced efficiency and potentially improved generalization. However, careful consideration must be given to the choice of transformation; a poorly chosen mapping could distort crucial information, rendering the latent space dynamics ineffective or even misleading. Moreover, ensuring contractivity in the latent space does not automatically guarantee contractivity in the original data space, unless specific conditions on the transformation are met. Therefore, theoretical analysis validating the mapping is crucial. Finally, interpreting the latent space itself can be challenging, but it may offer valuable insights into hidden relationships within the original data that were not apparent in the high-dimensional representation. In summary, while latent space modeling is a promising technique for simplifying and effectively learning the dynamics of complex systems, careful design and validation are critical for its success.
Diffeomorphism Effects#
Diffeomorphisms, in the context of this research paper, are transformations that warp the data space to facilitate learning of contracting dynamics. Their effects are multifaceted. First, they provide flexibility to handle datasets whose inherent dynamics are not simply equilibrium-contracting; by altering the metric in the transformed latent space, contractivity can be ensured even for complex datasets. Second, diffeomorphisms indirectly shape the learned contraction metric; while the model learns contractivity in the latent space, the choice of diffeomorphism influences how this contractivity manifests in the original data space. This allows for learning of dynamics that contract with respect to metrics beyond the simple Euclidean metric, expanding the range of systems that the model can represent. The interplay between the diffeomorphism and the learned dynamics is crucial; joint training is essential to ensure effective learning, as training them independently can lead to mismatched spaces and poor performance. In essence, diffeomorphisms are not merely mathematical tools, but integral components of the learning architecture, enabling broader applicability and richer expressive power in the learning of contracting dynamical systems.
Contraction Metrics#
Contraction metrics are crucial in the study of dynamical systems, providing a powerful tool to analyze stability and robustness. They quantify the rate at which trajectories of a system converge, offering a more nuanced understanding than traditional Lyapunov methods. The choice of metric significantly impacts the analysis, with different metrics highlighting various aspects of system behavior. Finding suitable contraction metrics can be challenging, often requiring sophisticated mathematical techniques. However, their ability to guarantee exponential convergence and robustness to perturbations makes them invaluable for designing stable and reliable systems, particularly in applications involving uncertainty or disturbances. The development of efficient computational methods for determining and utilizing contraction metrics remains an active area of research. This is especially important for high-dimensional systems where standard techniques become computationally expensive.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the framework to handle more complex dynamical systems such as those exhibiting limit cycles or chaotic behavior would significantly broaden its applicability. Investigating the theoretical properties of the learned diffeomorphisms and their impact on the contraction metric is crucial for deeper understanding and improved model design. Developing more efficient training methods to overcome the computational cost associated with high-dimensional data and complex architectures is also a key area. Furthermore, applying this method to various real-world applications in robotics, control systems, and other domains would validate its effectiveness and uncover new challenges.
More visual insights#
More on figures
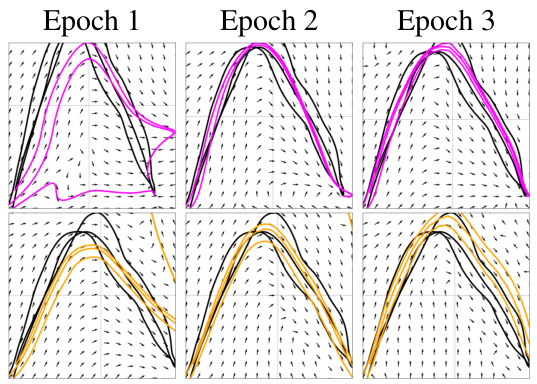
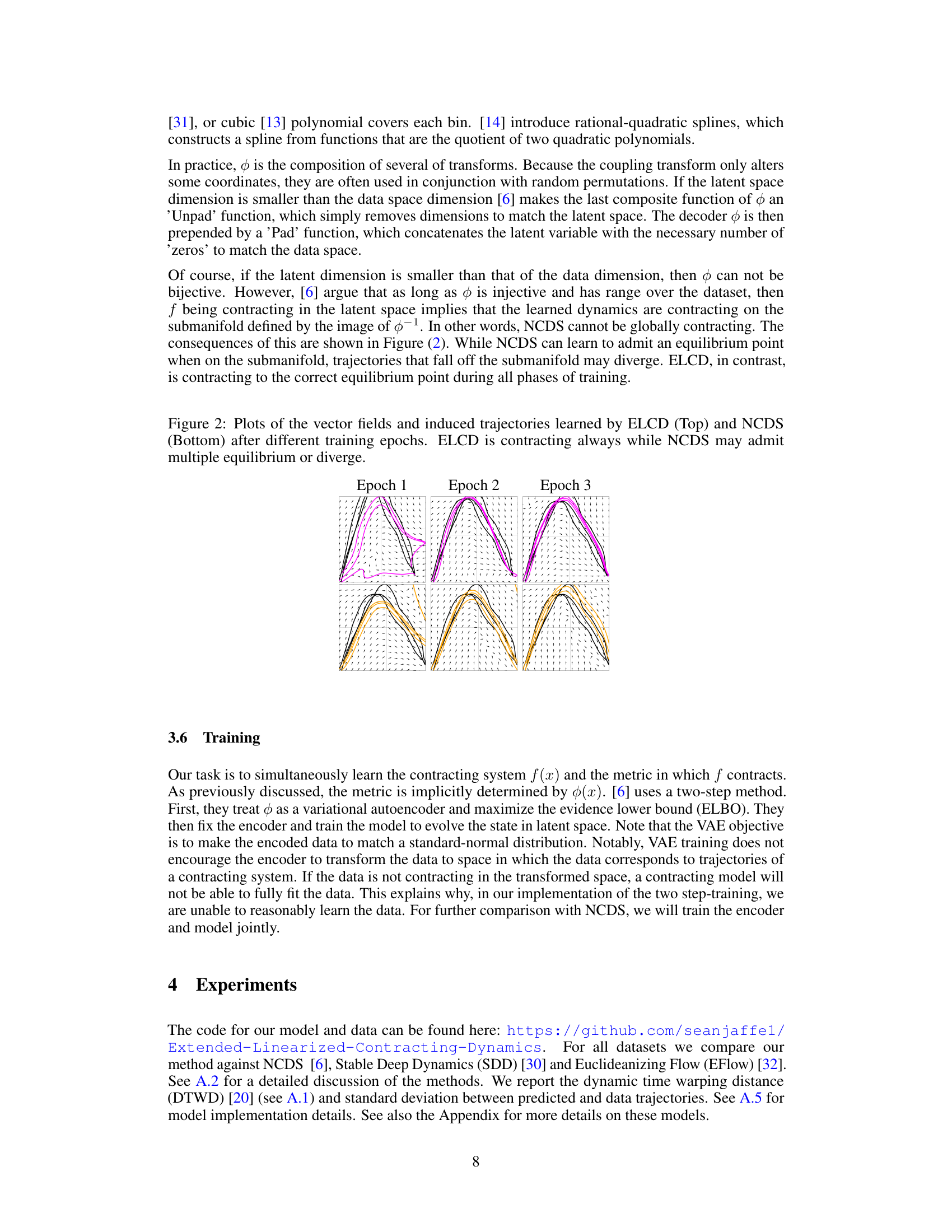
This figure compares the performance of ELCD and NCDS across three training epochs. The top row shows ELCD’s vector field and trajectories, demonstrating consistent contraction towards a single equilibrium point across all epochs. The bottom row shows NCDS, where the vector field and trajectories exhibit multiple equilibria and divergence, indicating a failure to maintain consistent contraction during training.
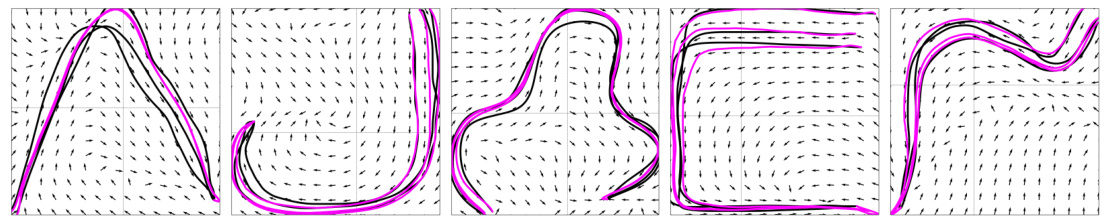
This figure shows four examples of 2D trajectories from the LASA dataset. Black lines represent the actual demonstration trajectories. Magenta lines show the trajectories produced by the ELCD model when trained on the dataset. The short black lines overlaid on the plots represent the learned vector field at various points in the state space. The velocity magnitudes of the vector field have been normalized for better visualization.
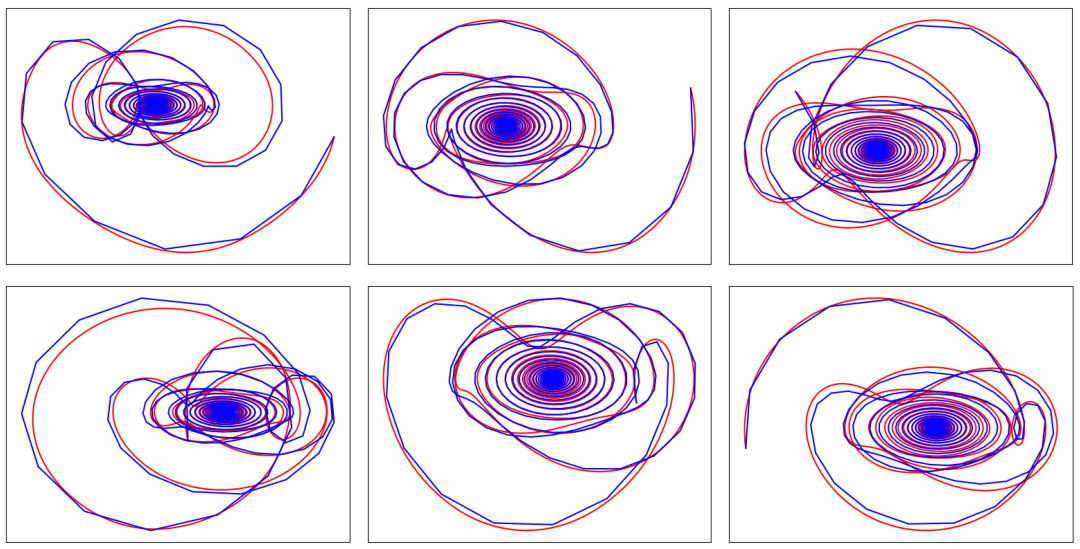
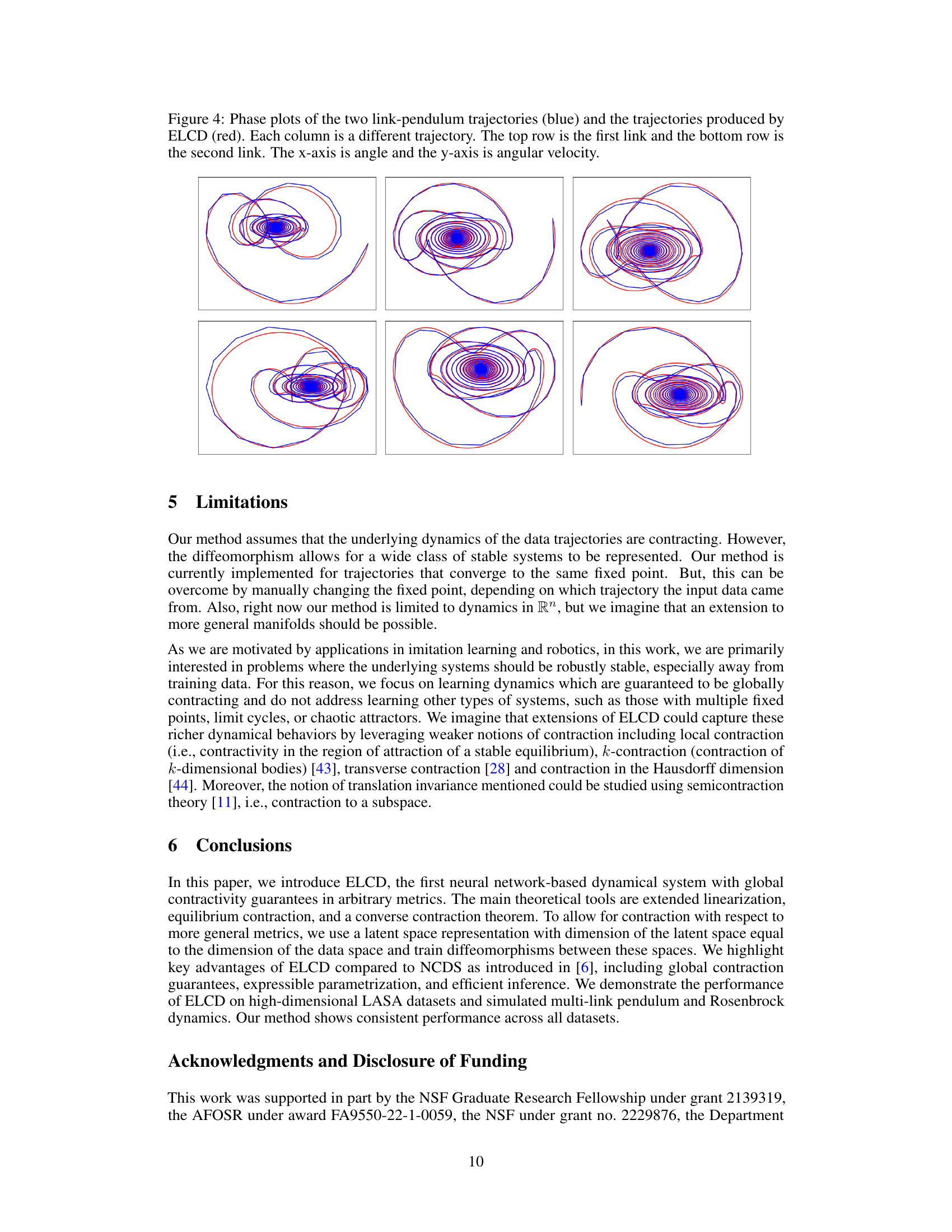
This figure shows a comparison of the trajectories of a two-link pendulum (blue) and the trajectories predicted by the ELCD model (red). Each column represents a different trajectory, with the top row showing the angle of the first link and the bottom row showing the angle of the second link. The x-axis represents the angle and the y-axis represents the angular velocity. The figure demonstrates the ELCD model’s ability to accurately predict the complex, oscillatory behavior of the pendulum.
Full paper#