ReLIZO: Sample Reusable Linear Interpolation-based Zeroth-order Optimization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in zeroth-order optimization due to its novel approach of reusing queries from previous iterations to significantly reduce computational cost without compromising accuracy. This is highly relevant given the resource-intensive nature of many real-world ZO applications and opens avenues for exploring more efficient gradient estimation strategies, impacting various fields like AI and AutoML.

Visual Insights

#

This figure compares the optimization performance of four different zero-order optimization methods (ZO-SGD, ZO-signSGD, ZO-AdaMM, and ReLIZO) across four distinct test problems from the CUTEst benchmark. Each problem has a different dimensionality (d), as indicated in the sub-captions. The plots show the objective function value over 500 iterations. The lines represent the average performance across three runs for each method, with shaded regions indicating the standard deviation.

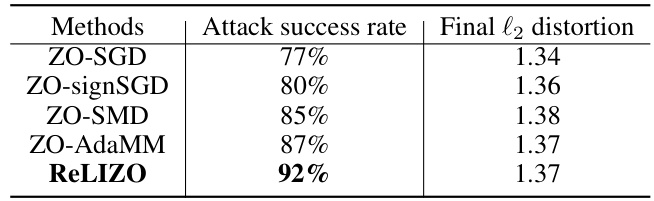
This table presents the results of a universal adversarial attack experiment, comparing the performance of ReLIZO against four other zeroth-order optimization methods. The key metrics compared are the attack success rate (percentage of successful attacks) and the final l2 distortion (the magnitude of the adversarial perturbation). All methods were run for 20,000 iterations on 100 images from the CIFAR-10 test dataset, with the goal of maintaining similar final l2 distortion across the methods for fair comparison. The table highlights the superior performance of ReLIZO in achieving a higher attack success rate compared to other methods while keeping the final l2 distortion relatively the same.

In-depth insights

#

Reusing ZO Queries

#

The concept of “Reusing ZO Queries” in zeroth-order optimization is a significant advancement. The core idea is to leverage previously computed function evaluations from prior iterations to reduce computational cost and query overhead, a crucial factor in scenarios with expensive function evaluations. This is particularly important for high-dimensional problems where obtaining sufficient samples for accurate gradient estimations can be computationally prohibitive. By cleverly incorporating past queries into the current gradient estimation, the method aims to reduce the number of new function evaluations required per iteration while maintaining the accuracy of the gradient approximation. This reuse strategy, however, requires careful consideration of maintaining appropriate sampling distributions to avoid introducing bias into the gradient estimate. The success of this approach heavily depends on the properties of the optimization landscape and the ability to select reusable queries that are relevant to the current optimization step. Further research could explore adaptive strategies for selecting reusable queries and analyze the impact of varying levels of query reuse on the convergence rate and overall optimization performance.

QCLP Gradient Estimation

#

The proposed method models gradient estimation as a Quadratically Constrained Linear Program (QCLP). This is a significant departure from traditional methods that either smooth the objective function (introducing bias) or rely on linear interpolation (requiring many samples). The QCLP formulation cleverly allows for the reuse of previously computed function evaluations, reducing computational cost and sample complexity. This is achieved by incorporating prior iterations’ queries into the current estimation, significantly improving efficiency without sacrificing accuracy. The analytical solution to the QCLP provides an efficient way to estimate gradients, unlike iterative methods that might be computationally expensive for high-dimensional problems. Decoupling the required sample size from the variable dimension is another key advantage, making the method scalable for large-scale problems. Overall, the QCLP approach offers a novel and efficient solution for zeroth-order optimization, by addressing some of the limitations of conventional methods.

Convergence Analysis

#

A rigorous convergence analysis is crucial for establishing the reliability and efficiency of any optimization algorithm. In the context of zeroth-order optimization, where gradient information is unavailable, convergence analysis becomes particularly challenging. The analysis often involves establishing bounds on the error between the estimated gradient and the true gradient, and relating this error to the convergence rate of the algorithm. A common approach involves using assumptions about the smoothness of the objective function (e.g., Lipschitz continuity of the gradient or Hessian). The analysis may demonstrate sublinear or linear convergence rates, depending on the specific algorithm and assumptions made. A key aspect is determining how the convergence rate depends on problem parameters such as dimensionality and the number of function evaluations. A strong convergence analysis provides confidence in the algorithm’s performance and guides the selection of hyperparameters. It also helps to understand the limitations of the algorithm, highlighting scenarios where it may not perform optimally.

Efficient Computation

#

Efficient computation is crucial for the practical applicability of any algorithm, and this research paper emphasizes this aspect by proposing a novel approach to reduce computational cost. Reusing prior queries is a key innovation that avoids redundant computations, making the method more efficient than traditional linear interpolation. By modeling the problem as a quadratically constrained linear program (QCLP) and deriving an analytical solution, the required sample size is decoupled from the variable dimension, making it scalable to high-dimensional problems. Furthermore, intermediate variables can be directly indexed, avoiding unnecessary recalculations. This strategy significantly lowers the computation complexity, accelerating the zeroth-order optimization process. The theoretical analysis and experimental results demonstrate the effectiveness of the proposed method in various applications, highlighting its efficacy and efficiency compared to existing approaches. The ability to reuse information while maintaining accuracy is a significant improvement.

Future Work

#

The ‘Future Work’ section of a research paper on zeroth-order optimization presents exciting avenues for improvement and extension. Addressing the limitations of requiring multiple function evaluations, perhaps through more sophisticated sampling techniques or leveraging surrogate models, is crucial for broader applicability. Investigating the impact of query cost in scenarios where evaluations are expensive is key to determining ReLIZO’s effectiveness in practical settings. Furthermore, exploring the algorithm’s robustness under various noise conditions and different problem structures warrants further investigation. Finally, extending ReLIZO’s applications to more complex optimization problems such as those encountered in reinforcement learning and evaluating its performance on extremely high-dimensional data would significantly broaden its impact and highlight the method’s true potential. A comprehensive analysis comparing ReLIZO with state-of-the-art methods across various applications and problem scales is also needed to establish its competitive advantage.

More visual insights

#

More on figures

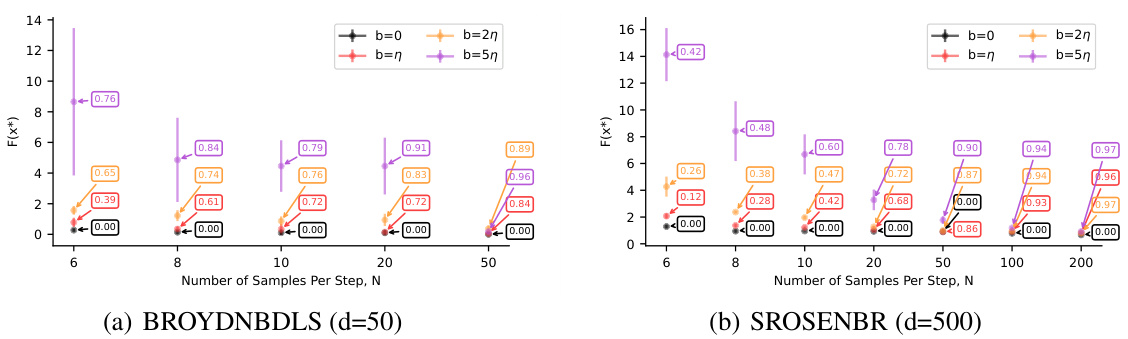
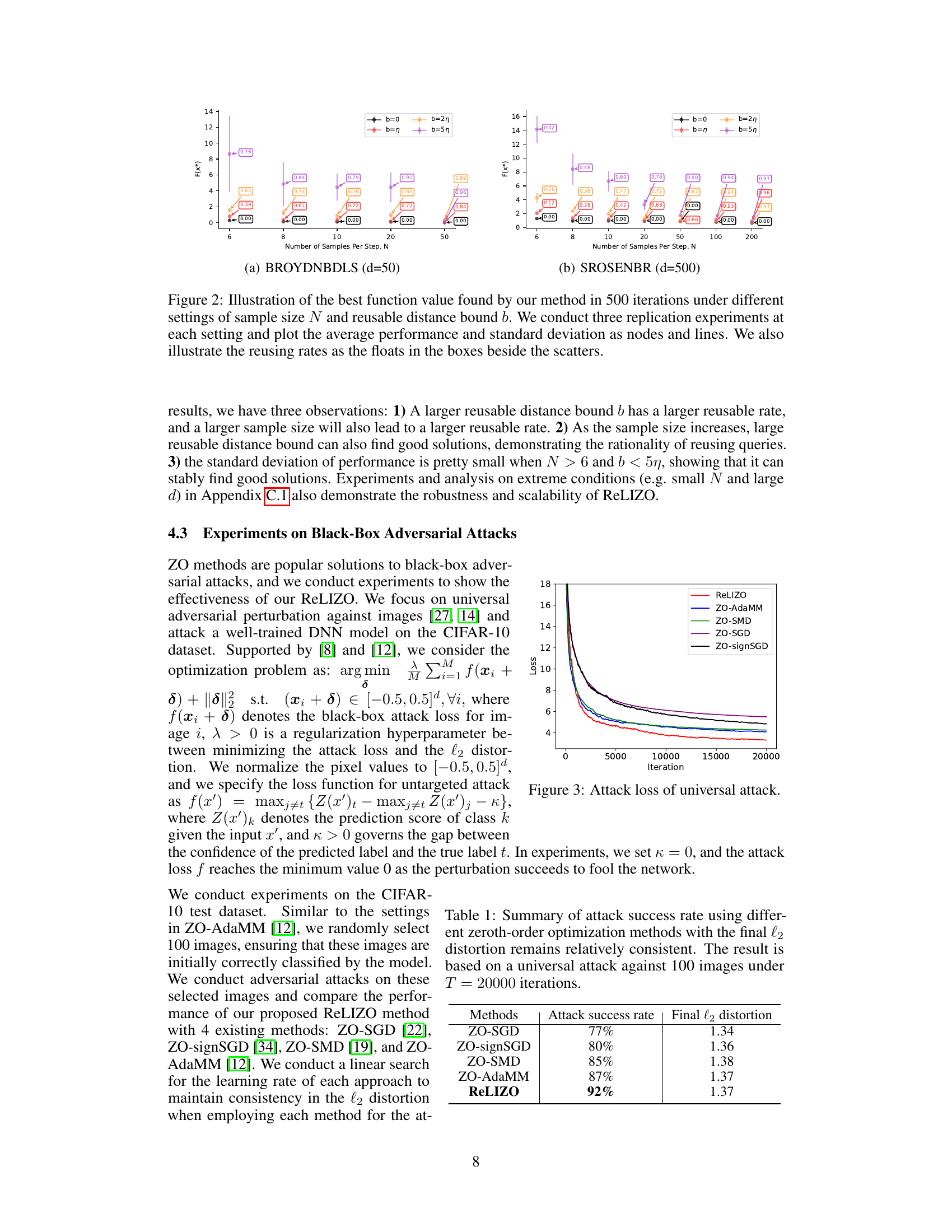
The figure shows the impact of sample size and reusable distance bound on the performance of the ReLIZO method. It plots the best objective function value achieved after 500 iterations for various sample sizes (N) and reusable distance bounds (b). Each point represents the average of three independent runs, with error bars indicating standard deviation. The floats in the boxes show the reuse rate for each configuration.

This figure shows the attack loss curves for universal adversarial attacks using five different zeroth-order optimization methods: ReLIZO, ZO-AdaMM, ZO-SMD, ZO-SGD, and ZO-signSGD. The x-axis represents the number of iterations, and the y-axis represents the attack loss. It demonstrates the comparative performance of ReLIZO against other methods in achieving a lower attack loss over the course of the optimization process.

This figure shows the results of ablation studies on the effect of sample size and reusable distance bound on the optimization performance. The x-axis represents the sample size (N), while the y-axis shows the best function value achieved after 500 iterations. Different colors represent different reusable distance bounds (b). Each point represents the average of three independent runs, and error bars show standard deviations. The numbers in the boxes indicate the reuse rate for each setting.

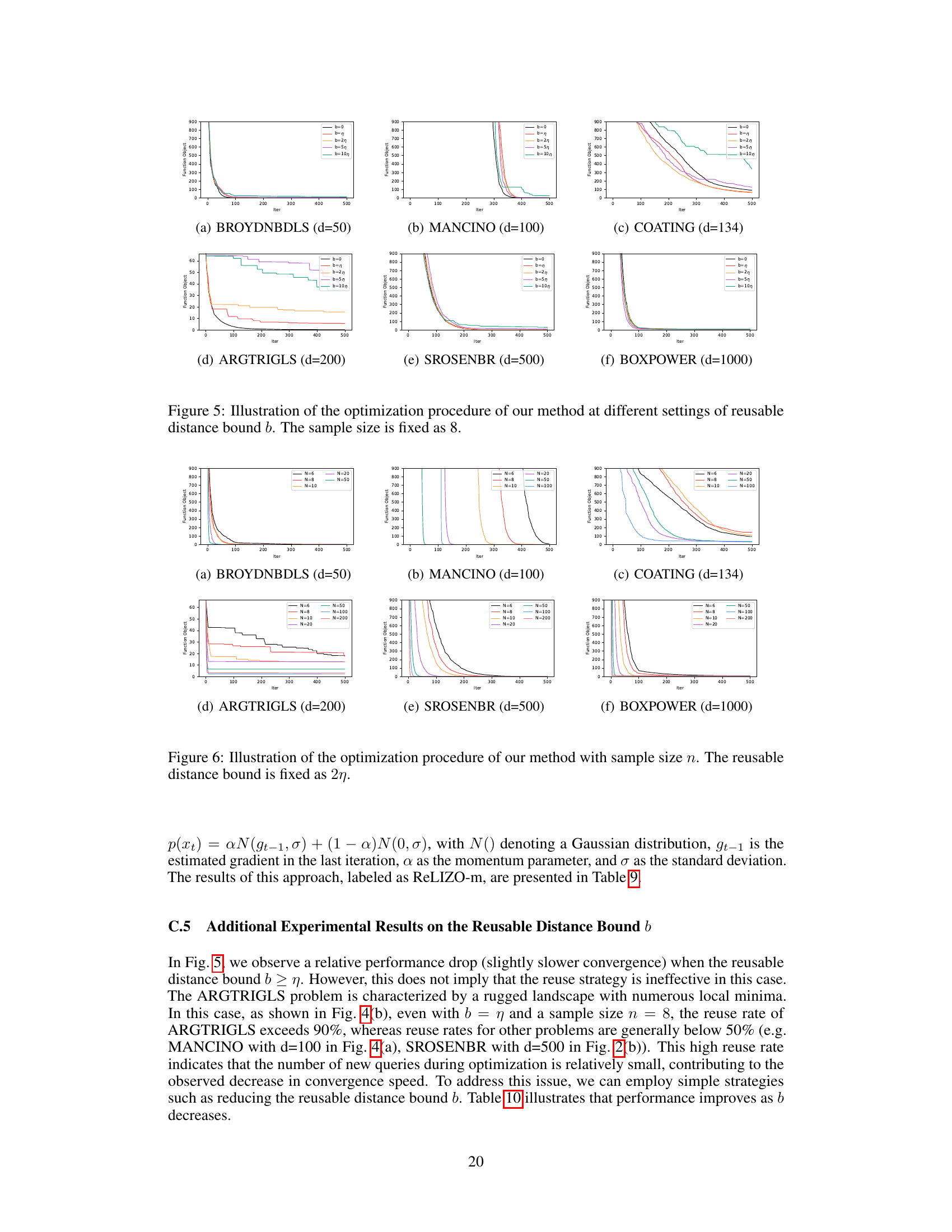
This figure shows the optimization curves obtained by the proposed ReLIZO method under different settings of reusable distance bound (b). The x-axis represents the number of iterations, and the y-axis represents the objective function value. Each curve corresponds to a different value of b, showcasing the impact of this hyperparameter on the convergence behavior of the optimization process. The sample size (n) is kept constant at 8 for all experiments. By varying ‘b’, the figure demonstrates how the reuse strategy affects optimization performance. The results displayed are typical for multiple runs of the optimization algorithm.

This figure compares the performance of ReLIZO against three other zeroth-order optimization methods (ZO-SGD, ZO-signSGD, ZO-AdaMM) across four different test problems from the CUTEst dataset. Each problem has a different dimensionality (d). The plots show the objective function value over 500 iterations. ReLIZO demonstrates faster convergence and lower standard deviation (more stable performance) compared to the other methods. The shaded area represents the standard deviation across three independent runs for each method.

More on tables

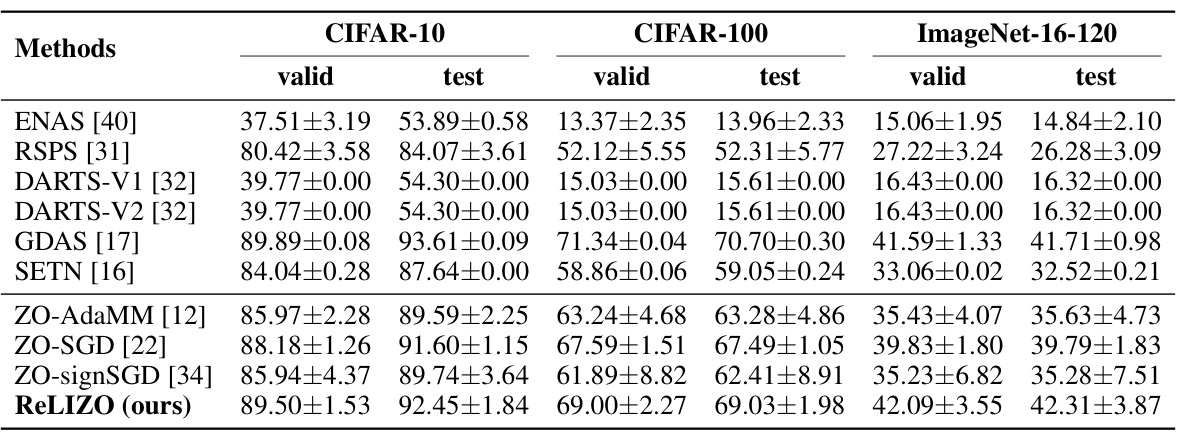
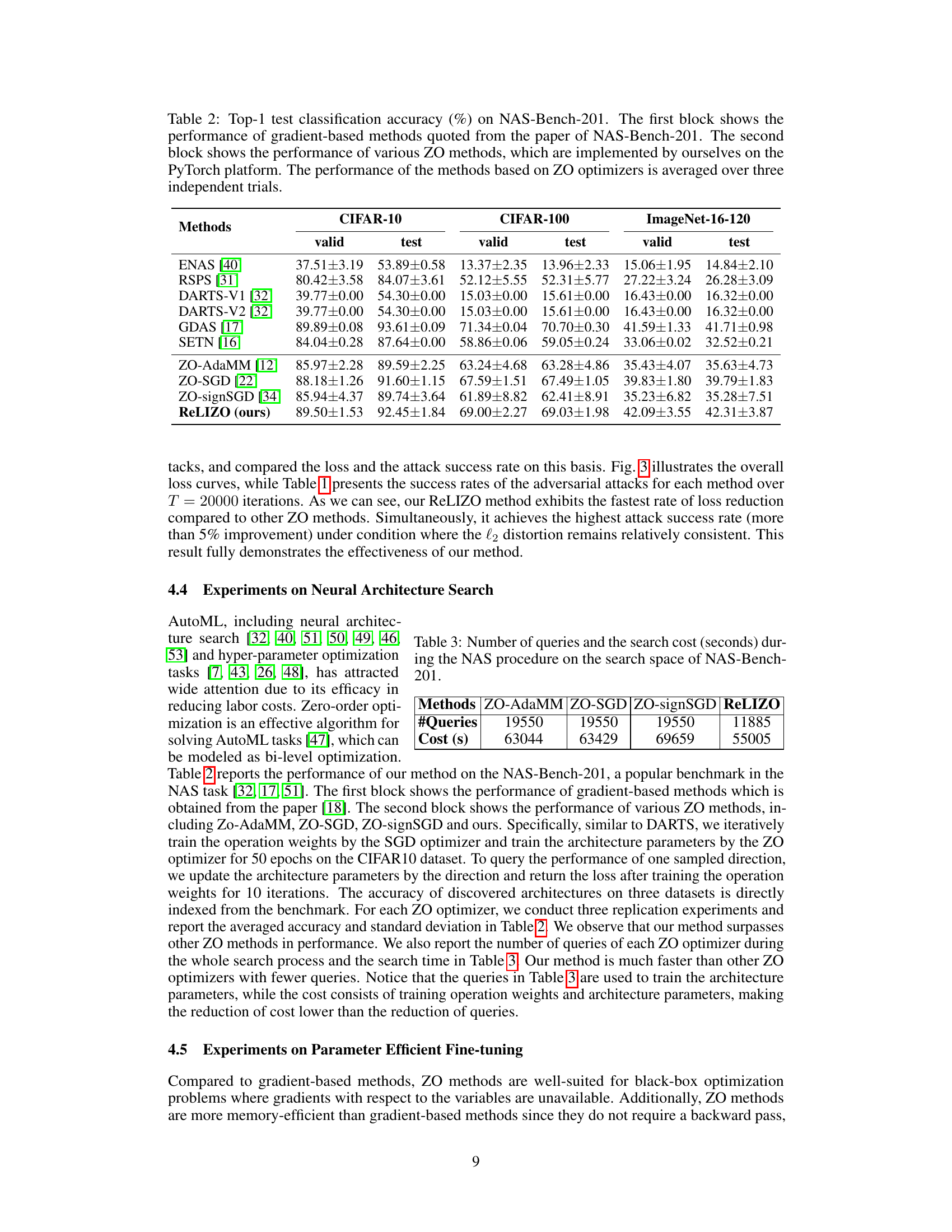
This table presents the top-1 test classification accuracy results on the NAS-Bench-201 dataset. It compares the performance of several gradient-based neural architecture search (NAS) methods with several zeroth-order optimization (ZO) methods. The gradient-based results are taken directly from the NAS-Bench-201 paper. The ZO method results were obtained by the authors of this paper using the PyTorch platform. For the ZO methods, the reported accuracies are averages across three independent trials.

This table presents a comparison of the number of queries and the time spent on the neural architecture search (NAS) task using different zeroth-order optimization (ZO) methods. It shows that the proposed ReLIZO method requires significantly fewer queries and less computation time than the other ZO methods while achieving comparable performance.

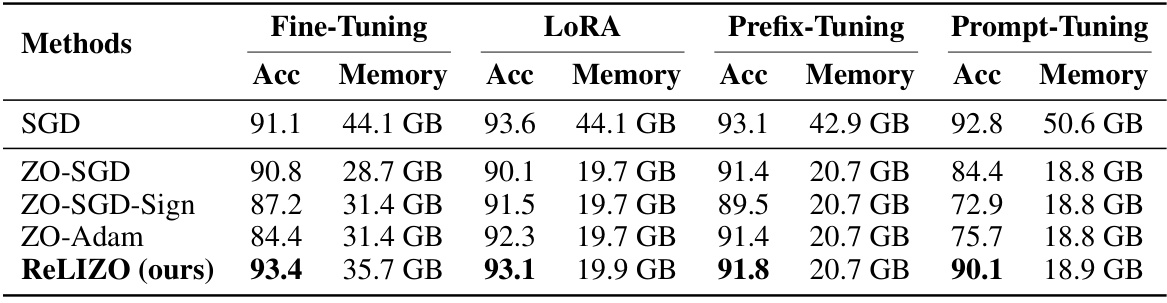
This table presents the results of several zero-order optimization methods and SGD, applied to fine-tune the OPT-1.3B language model on the SST2 dataset, using four different parameter-efficient fine-tuning techniques: full fine-tuning, LoRA, prefix-tuning, and prompt-tuning. The table shows the accuracy achieved and memory usage for each method and technique.

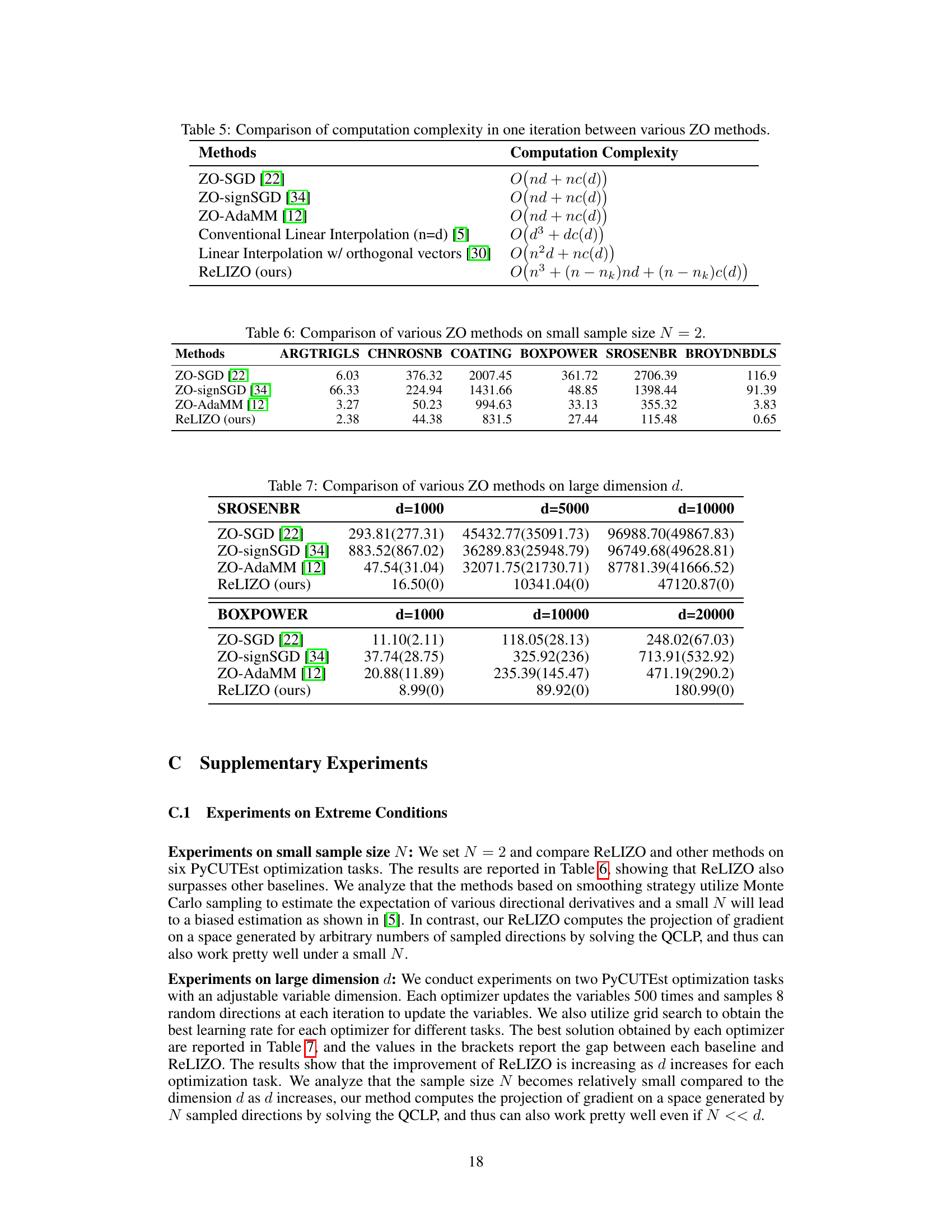
This table compares the computation complexity of different zeroth-order optimization methods in a single iteration. The complexity is expressed in big O notation and depends on the dimension of variables (d), sample size (n), and the cost of querying function evaluations (c(d)). ReLIZO’s complexity is shown to be advantageous when reusing queries from previous iterations (nk).

This table compares the performance of four zeroth-order optimization (ZO) methods: ZO-SGD, ZO-signSGD, ZO-AdaMM, and ReLIZO (the proposed method) on six different optimization problems from the CUTEst test suite. The sample size N is fixed at 2, which represents a small sample regime, to evaluate the robustness of the algorithms in data-scarce scenarios. The table shows the objective function values achieved by each method for each problem. Lower values indicate better performance.

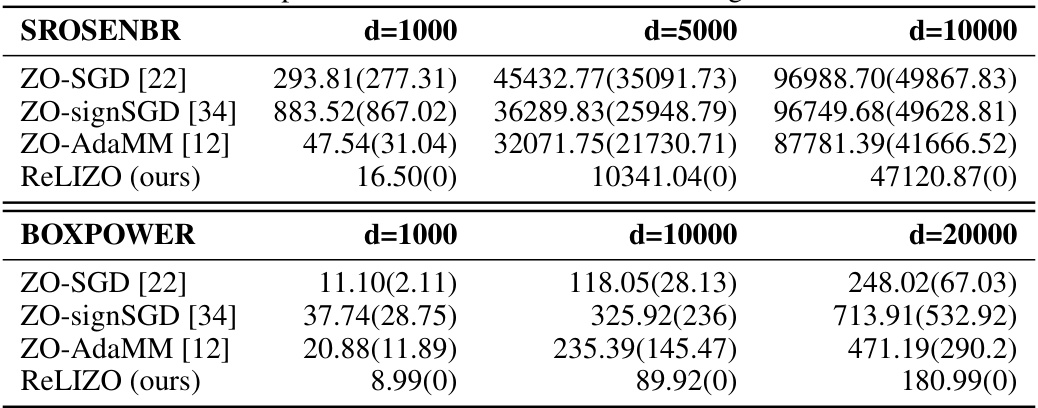
This table compares the performance of four zeroth-order optimization methods (ZO-SGD, ZO-signSGD, ZO-AdaMM, and ReLIZO) on the BOXPOWER and SROSENBR problems from the CUTEst benchmark. The comparison is done for different dimensions (d) of the problem’s variables: d=1000, d=5000, and d=10000 for SROSENBR; and d=1000, d=10000, and d=20000 for BOXPOWER. The numbers in parentheses represent the standard deviation of the results across multiple runs. The table highlights the effectiveness of ReLIZO in handling high-dimensional optimization problems, showcasing significantly lower objective function values compared to other methods.

This table presents a detailed breakdown of the query counts during the optimization process for several benchmark problems. It shows the number of queries from line search (#LS), the total number of queries (#Queries), the number of reused queries (#Reused), and the total number of queries that would have been needed without the query reuse strategy (N x T). This demonstrates the efficiency gains achieved by ReLIZO’s query reuse mechanism, showing significantly fewer queries than standard methods.

This table compares the top-1 test classification accuracy of different neural architecture search (NAS) methods on the NAS-Bench-201 benchmark. It contrasts gradient-based methods with zeroth-order (ZO) optimization methods. The ZO methods were implemented by the authors and their performance is averaged across three independent trials.

This table presents the objective function values after 500 and 2000 iterations of the ReLIZO algorithm, along with the corresponding total reuse rates, for various values of the reusable distance bound (b). The results show how the objective function value and reuse rate change as the reusable distance bound is increased. A larger reusable distance bound allows for a higher reuse rate, but may lead to a slightly higher objective function value.

This table presents the objective function values obtained after 500 and 2000 iterations of the ReLIZO algorithm, using different values for the reusable distance bound (b). It also shows the overall reuse rate achieved for each value of b. The results demonstrate the impact of the reusable distance bound on both the optimization performance and the query reuse efficiency. A larger reusable distance bound generally leads to higher reuse rates but can potentially affect the quality of the optimization results.

Full paper

#