↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Foundation models, while powerful, often produce unreliable outputs in high-stakes applications like medical diagnosis. Ensuring these outputs align with human expectations (alignment) is crucial but challenging. Existing methods either modify outputs or generate multiple outputs until a reliable one is found; both are impractical. This paper tackles this problem by focusing on output selection rather than modification or generation.
The proposed approach, Conformal Alignment, uses a learned alignment predictor and a calibrated threshold to select outputs that are likely to be aligned. Importantly, it provides distribution-free, finite-sample guarantees on the proportion of selected outputs meeting an alignment criterion. The method is demonstrated on question answering and radiology report generation tasks, showing strong results and highlighting the informativeness of various features in predicting alignment.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with foundation models due to its novel approach to ensuring output reliability. It directly addresses the critical issue of trustworthiness in model outputs and provides a practical framework with provable guarantees. This opens doors for more responsible deployment of foundation models across various high-stakes applications, where reliability and alignment are paramount. The distribution-free nature of the method broadens its applicability beyond specific model architectures and data distributions, impacting a wider range of researchers.
Visual Insights#

This figure illustrates the workflow of Conformal Alignment in the context of radiology report generation. It shows how a foundation model generates reports for chest X-rays. A subset of high-quality reference data (with human-expert reports) is used to train an alignment predictor. This predictor then scores the new model-generated reports. Reports surpassing a calibrated threshold are certified as trustworthy, while reports below the threshold are flagged as uncertain and require human review. The process ensures that a guaranteed fraction of the selected reports are actually aligned with human expert opinions.

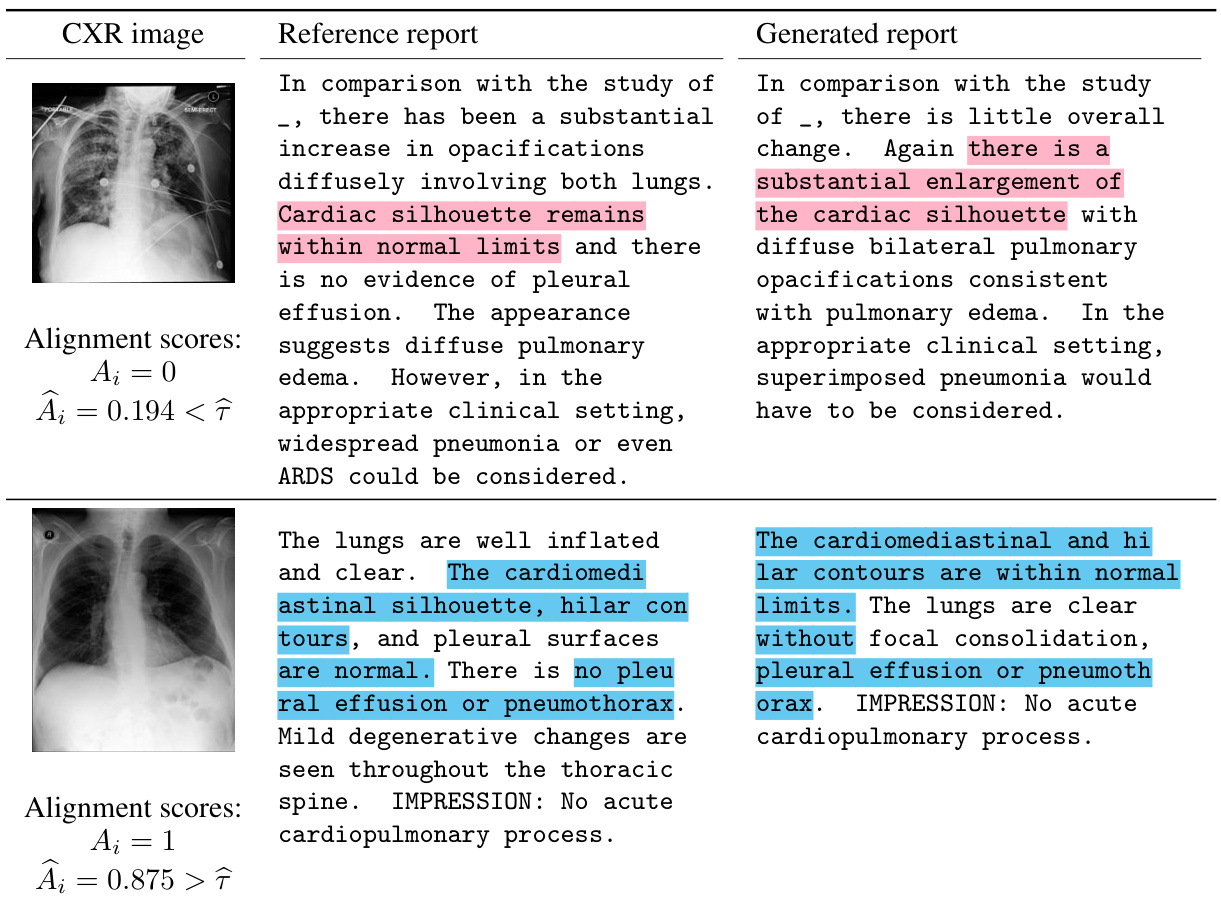
This table shows four examples from the TriviaQA dataset to illustrate how Conformal Alignment selects trustworthy outputs. For each example, it lists the question, the reference answer, the generated answer, and the alignment scores (A and A_hat). The selection threshold is 0.388. The examples show that the method is able to accurately identify trustworthy outputs in a variety of scenarios.
In-depth insights#
Conformal Alignment#
Conformal Alignment, as a concept, offers a robust framework for ensuring that outputs from foundation models align with user-defined criteria. Its core strength lies in providing probabilistic guarantees, unlike many existing methods. This is achieved by leveraging conformal prediction techniques to identify and certify trustworthy model outputs. The framework’s generality is noteworthy, as it doesn’t rely on specific model architectures or data distributions. By training an alignment predictor on reference data and using a data-dependent threshold, Conformal Alignment makes decisions about which outputs to trust and which to reject. The method is demonstrably effective in practice, as shown by its application to question answering and radiology report generation tasks, while remaining computationally lightweight. A significant advantage is the direct use of model outputs without modification, thus preserving informativeness and avoiding potential drawbacks of post-hoc adjustments. However, challenges may arise with respect to the choice of alignment criterion and the amount of high-quality reference data needed for accurate training.
FDR Control#
The concept of FDR (False Discovery Rate) control is central to the proposed Conformal Alignment framework. It addresses the crucial issue of ensuring that when selecting model outputs deemed ’trustworthy’ according to some criterion, the proportion of incorrectly selected outputs (false discoveries) remains below a pre-specified threshold. This is not just about accuracy, but about managing risk, especially critical in high-stakes applications like medical diagnosis. The authors leverage the Conformalized Selection framework to achieve guaranteed FDR control, regardless of the underlying model or data distribution. This distribution-free guarantee is a significant strength, providing robust performance even with limited reference data. The method’s efficiency is highlighted by the ability to certify trustworthy outputs without modifying model predictions, offering a lightweight and practical approach that can be widely adopted in different settings.
QA & CXR Results#
A hypothetical ‘QA & CXR Results’ section would analyze the performance of a Conformal Alignment model on question answering (QA) and chest X-ray (CXR) report generation tasks. For QA, the analysis would likely focus on metrics such as accuracy, precision, recall, and F1-score, comparing the model’s performance to baselines and investigating the impact of different features on alignment prediction. The CXR portion would probably assess the model’s ability to generate accurate and aligned reports, possibly using metrics like BLEU or ROUGE scores and examining whether the model successfully identifies trustworthy outputs. A key aspect of both analyses would be evaluating the effectiveness of Conformal Alignment in controlling the false discovery rate (FDR) while maintaining high power. The results would ideally show that Conformal Alignment improves both accuracy and trustworthiness of model outputs in a statistically significant way, especially for high-stakes applications.
Feature Analysis#
A thorough feature analysis is crucial for understanding model performance in any machine learning task. In this context, a careful selection of features that capture the essence of alignment becomes critical. The analysis should investigate the informativeness of individual features, assessing their contribution to alignment prediction accuracy. This might involve comparing the performance of models trained on individual features versus those trained on combinations of features. Feature interaction effects also need to be considered—how multiple features work together to predict alignment. By analyzing feature importance scores (e.g., from SHAP values or tree-based model feature importance), the study can pinpoint the most influential features and those that may be redundant or less relevant. Quantifying uncertainty associated with each feature is also relevant; some features might be more reliably informative than others. Finally, the interpretability of selected features is key for understanding the model’s decision-making process and for building trust in the alignment guarantee.
Future Work#
The paper’s “Future Work” section could explore several promising avenues. Extending Conformal Alignment to handle more complex output formats, beyond simple classifications or scores, would significantly broaden its applicability. This could involve adapting the framework for structured data, sequences, or even generative outputs. A critical area is investigating alternative alignment criteria and their impact on the framework’s performance and interpretability. Exploring criteria beyond simple thresholds, perhaps using more nuanced metrics tailored to specific downstream tasks, could be particularly valuable. The current work relies on relatively simple model architectures for alignment prediction; future work should explore more sophisticated models, potentially incorporating domain expertise or incorporating uncertainty estimates directly into the model. Finally, thorough empirical evaluation on a wider range of foundation models and tasks is needed to demonstrate the framework’s generalizability and robustness. This would also help uncover its limitations and guide future improvements.
More visual insights#
More on figures
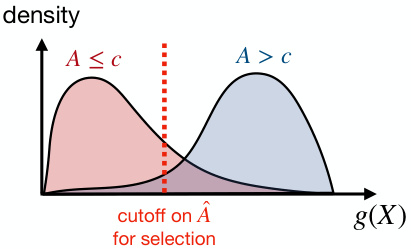
This figure illustrates the asymptotic selection rule used in Conformal Alignment. It shows the density curves of the predicted alignment scores g(X) for units with true alignment scores A below the threshold c (red curve) and above the threshold c (blue curve). The red dashed line represents the cutoff value on the predicted alignment scores that determines whether a unit is selected (right side) or not (left side). The area under the blue curve to the right of the cutoff represents the asymptotic power (the fraction of truly aligned units that are selected), while the area under the red curve to the right of the cutoff represents the false discovery rate (FDR) – controlled at the desired level alpha by the threshold.
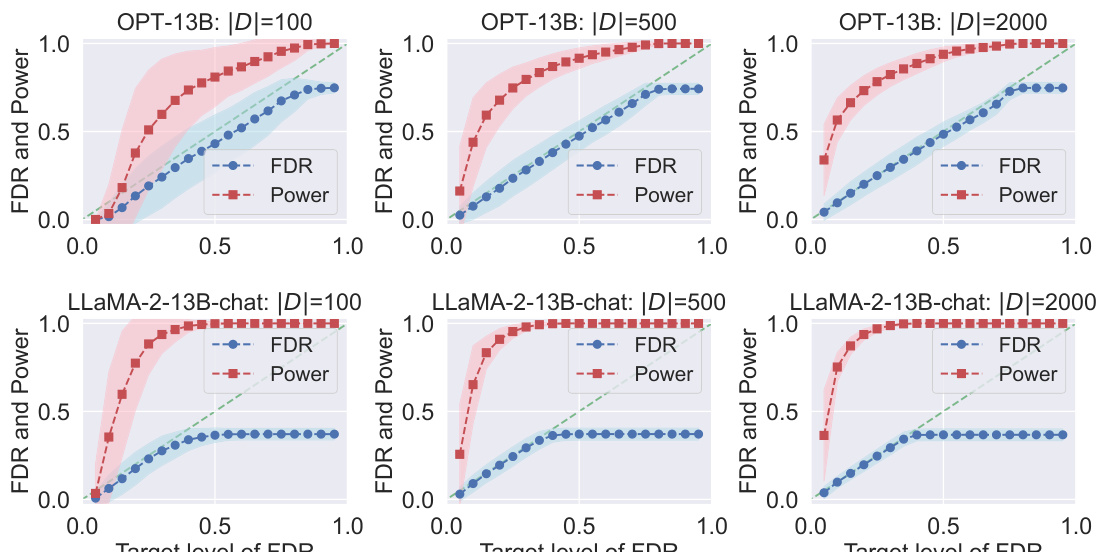
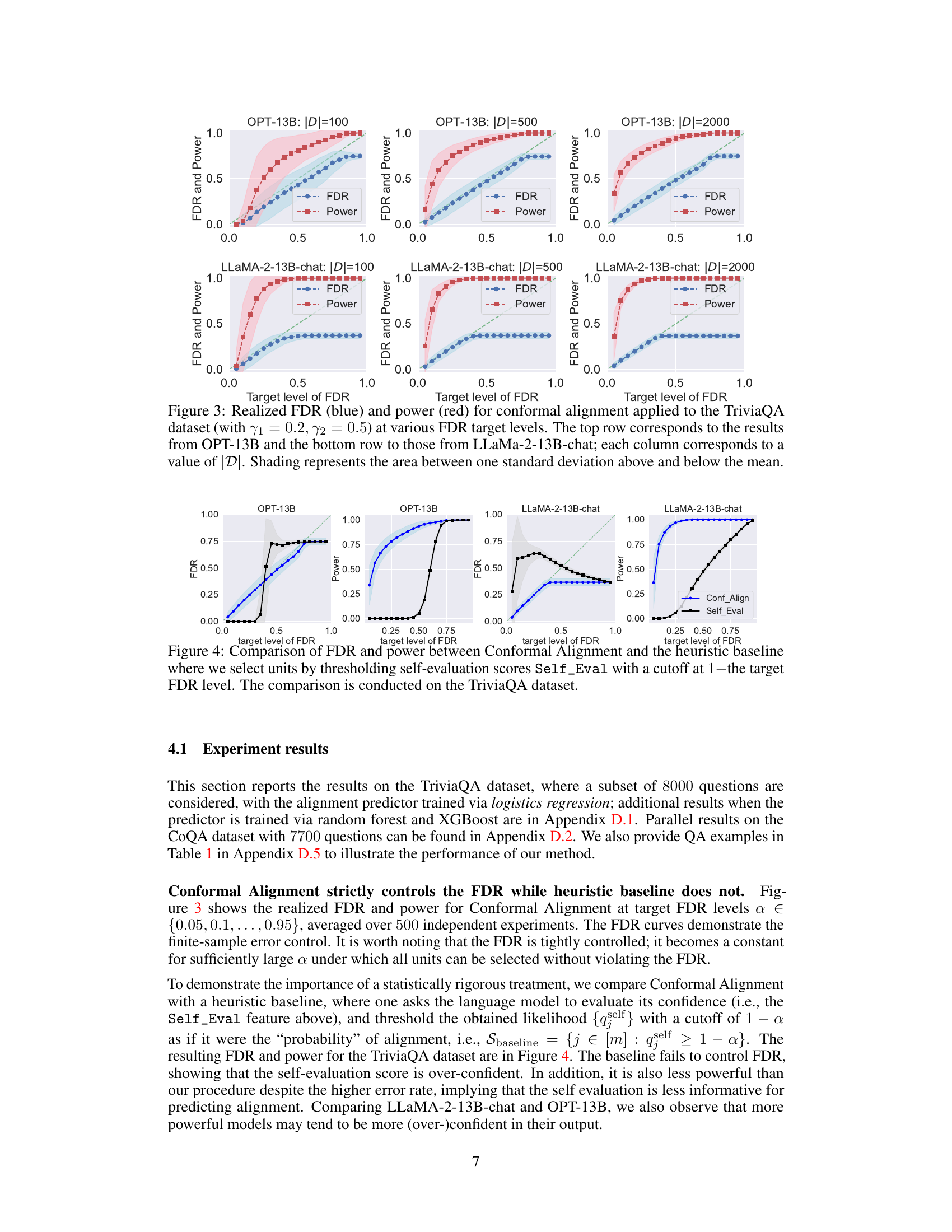
This figure displays the results of applying Conformal Alignment to the TriviaQA dataset for different FDR target levels. It shows the realized (actual) FDR and power for two different language models, OPT-13B and LLaMA-2-13B-chat, with varying sizes of the reference dataset |D|. Each subplot represents a specific |D| value, and the shading in the plot represents the variability (standard deviation) of the results.
This figure shows the results of applying Conformal Alignment to the TriviaQA dataset with different FDR target levels (α). The plots show the realized (actual) FDR (blue line) and power (red line) for both OPT-13B and LLaMA-2-13B-chat language models. The results are shown for three different sizes of the reference dataset |D| (100, 500, and 2000). Shading around the lines indicates the standard deviation. The figure demonstrates that the Conformal Alignment method maintains the FDR at or below the target level while achieving reasonable power, and shows the effect of the reference dataset size on performance.
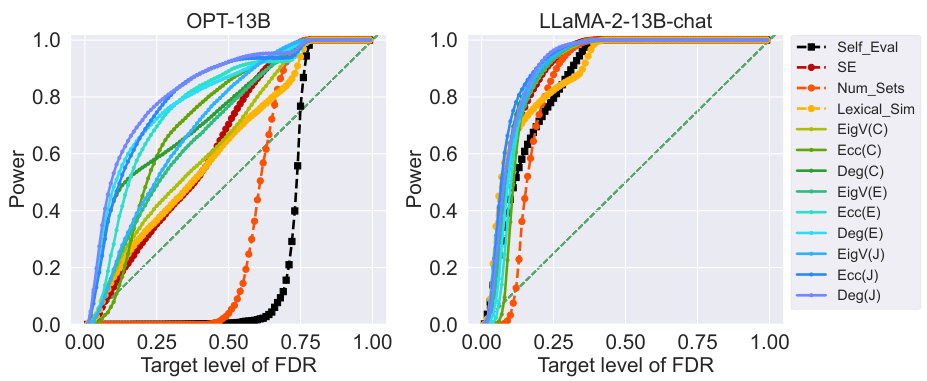
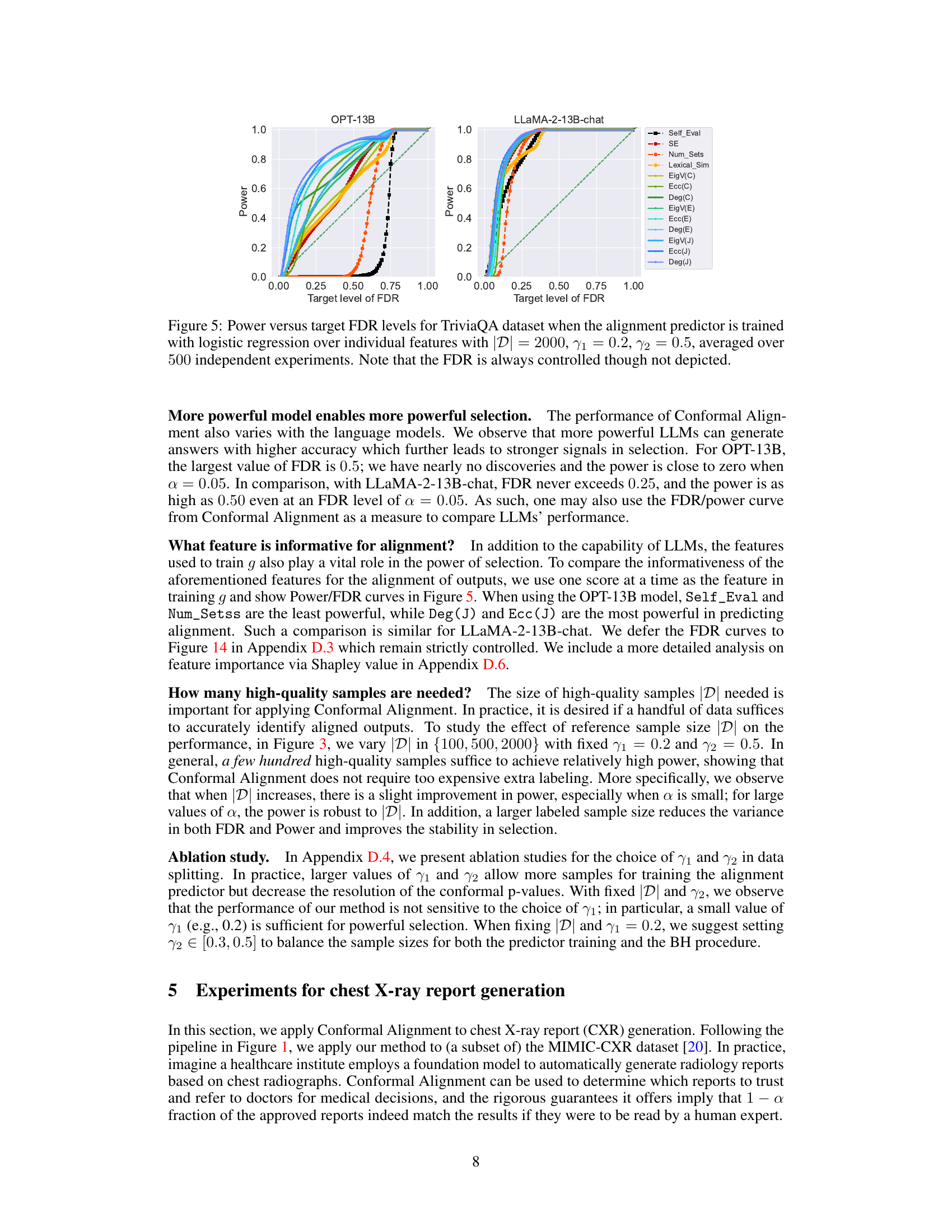
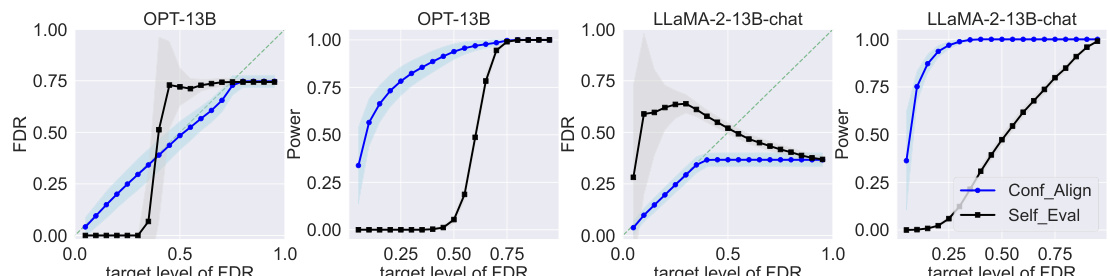
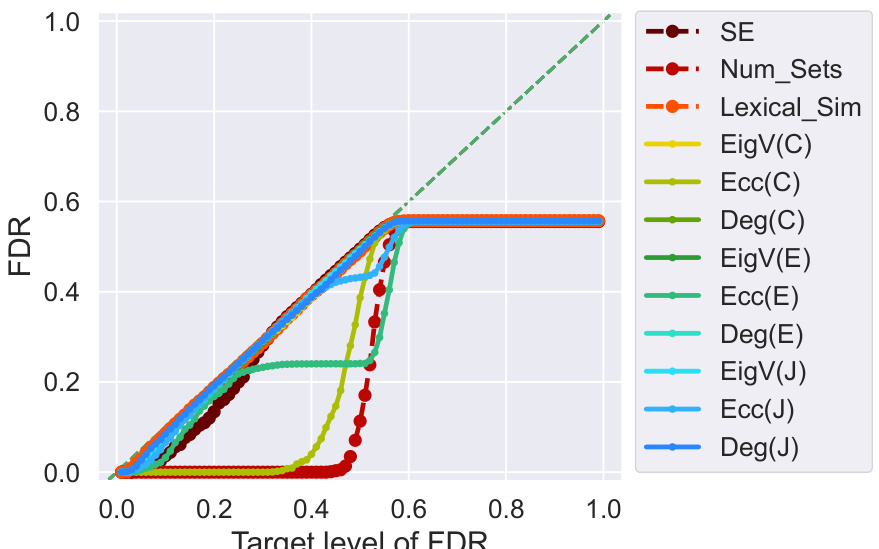
This figure shows the power of Conformal Alignment at various FDR target levels when using different individual features to train the alignment predictor. The experiment is conducted on the TriviaQA dataset with a fixed sample size of 2000 high-quality samples. The results are averaged over 500 independent runs and show how well each individual feature contributes to the model’s ability to identify trustworthy units (high power). Although not explicitly shown, the figure indicates that the FDR (false discovery rate) remains controlled at the specified levels for all features.

This figure displays the results of applying Conformal Alignment to the TriviaQA dataset for different target false discovery rates (FDR). It shows the actual FDR achieved (blue) and the statistical power of the method (red) across various settings. Different rows represent results from different language models (OPT-13B and LLaMA-2-13B-chat) and columns show how the results change with varying sizes of the reference dataset |D|. The shaded area around the lines shows the standard deviation of the results across multiple runs, indicating the variability in performance.

This figure shows the power of Conformal Alignment for different individual features used in training the alignment predictor on the TriviaQA dataset. The x-axis represents the target FDR level (false discovery rate), and the y-axis represents the power (the proportion of correctly selected units). Each line represents a different feature, showing how well each feature performs in identifying trustworthy units given a target FDR level. The figure demonstrates that even though the FDR is always controlled (not shown), different features exhibit varying power, highlighting their differing informativeness for identifying aligned outputs.

The figure shows a pipeline of the Conformal Alignment method in the context of radiology report generation. It begins with an LLM generating reports for chest X-rays. These reports are then assessed for alignment with human expert reports using an alignment predictor trained on human-quality reference data. A calibrated cutoff threshold then selects a subset of reports deemed trustworthy (meeting a user-specified alignment criterion), with a guaranteed FDR. Uncertain reports can be reviewed by human experts. This diagram visually represents the core workflow of the Conformal Alignment algorithm applied to a real-world medical scenario.

This figure shows the workflow of Conformal Alignment in a radiology report generation example. It begins with test prompts (X-ray scans) inputted into a large language model (LLM) that generates reports. Human-quality data (reference data with ground-truth alignment) is used to train an alignment predictor, which then assesses whether a generated report aligns with human values. A calibrated cutoff determines which LLM reports are deemed reliable enough for deployment, while reports below the threshold are flagged for human review. The process is designed to guarantee a minimum percentage of reliable outputs.
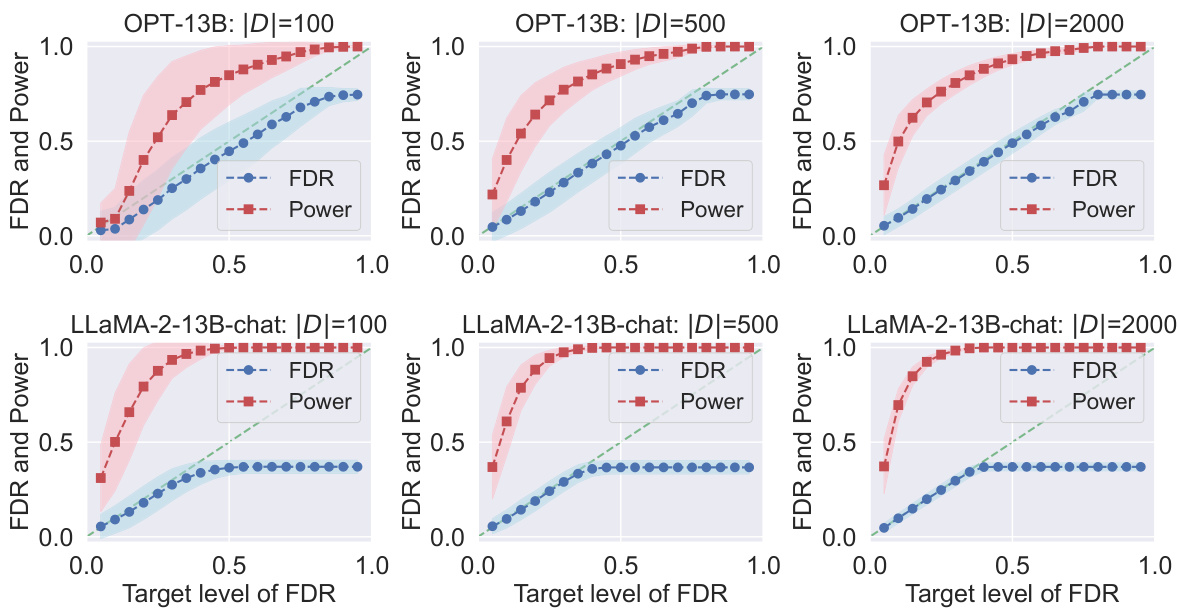
This figure displays the results of applying Conformal Alignment to the TriviaQA dataset for different target false discovery rates (FDR). It shows the realized (actual) FDR and power achieved for two different language models (OPT-13B and LLaMA-2-13B-chat) and three different sizes of the reference dataset |D|. The plots demonstrate the effectiveness of Conformal Alignment in controlling FDR while achieving a reasonable power.

This figure displays the results of applying conformal alignment to the TriviaQA question answering dataset. It shows the observed False Discovery Rate (FDR) and power for different target FDR levels, using two different language models (OPT-13B and LLaMa-2-13B-chat) and three different sizes of the reference dataset |D|. The shaded areas represent the standard deviation around the mean values, providing a sense of variability in the results.
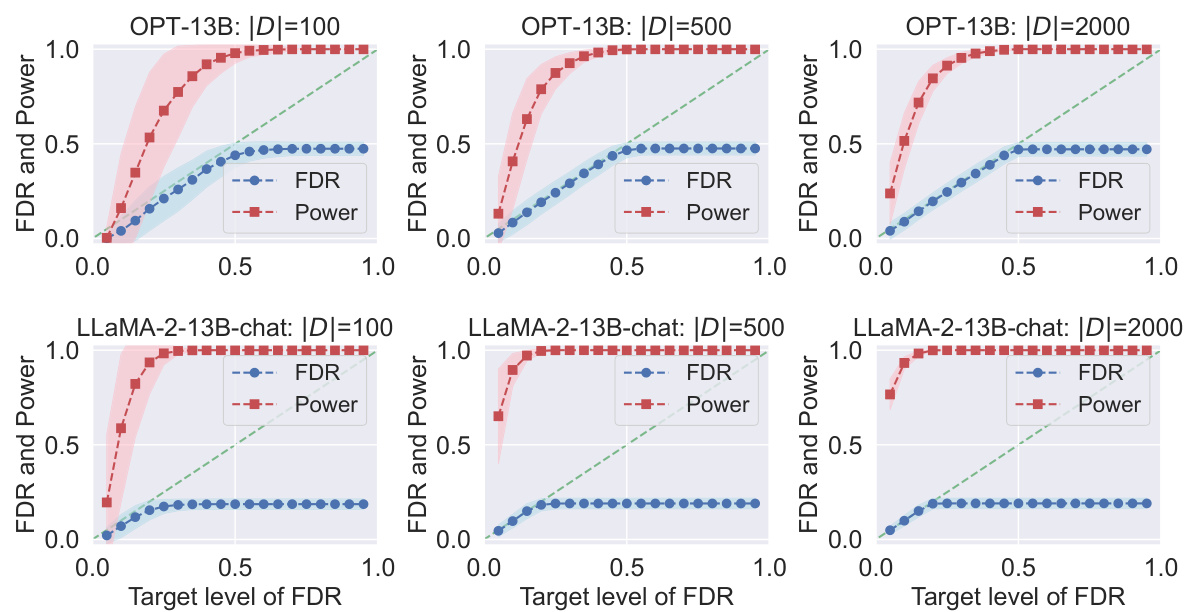
This figure shows the performance of Conformal Alignment in terms of realized FDR and power for different target FDR levels on the TriviaQA dataset. The results are displayed for two different language models (OPT-13B and LLaMa-2-13B-chat) and three different sizes of the reference dataset (|D|). The shaded areas represent the standard deviation around the mean values, highlighting the variability in performance. The plots demonstrate the ability of Conformal Alignment to maintain FDR control while achieving reasonable power.
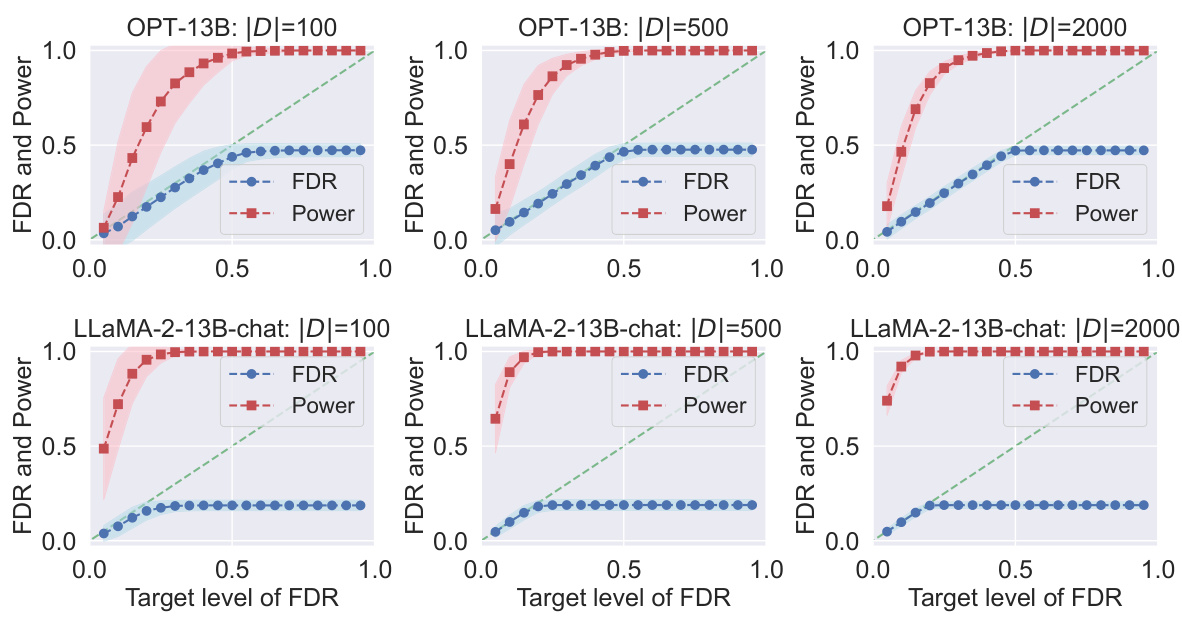
This figure displays the results of applying Conformal Alignment to the TriviaQA question answering dataset. It shows the observed False Discovery Rate (FDR) and power for different target FDR levels (the desired level of FDR). The results are shown for two different language models (OPT-13B and LLaMa-2-13B-chat) and three different sizes of the reference dataset |D|. The shaded areas represent the standard deviation around the mean FDR and power for each condition. This visualization demonstrates how well Conformal Alignment controls the FDR while maintaining reasonable power for various settings.

This figure displays the results of applying conformal alignment to the TriviaQA dataset. The plots show the realized false discovery rate (FDR, in blue) and power (in red) for different target levels of FDR. The experiment uses two different language models (OPT-13B and LLaMa-2-13B-chat) and varies the size of the reference dataset |D| (100, 500, and 2000). Shaded regions show the standard deviation around the mean values. The plots demonstrate that conformal alignment tightly controls FDR while maintaining reasonable power, and that the power increases with a larger reference dataset.

This figure displays the results of applying Conformal Alignment to the TriviaQA dataset. It shows the realized False Discovery Rate (FDR) and power at various target FDR levels for two different language models, OPT-13B and LLaMa-2-13B-chat, and three different sizes of the reference dataset (|D|). The plots demonstrate that Conformal Alignment successfully controls the FDR while maintaining reasonable power. Shading illustrates the standard deviation.

This figure displays the power of Conformal Alignment against the target FDR level, using logistic regression as the alignment predictor. The experiment is conducted on the TriviaQA dataset with specific hyperparameters (|D|=2000, γ₁=0.2, γ₂=0.5). Individual features are used to train the predictor, and the results are averaged over 500 independent runs. While the plot shows power, it’s important to note that the FDR is always kept below the target level, although not explicitly shown in the graph.
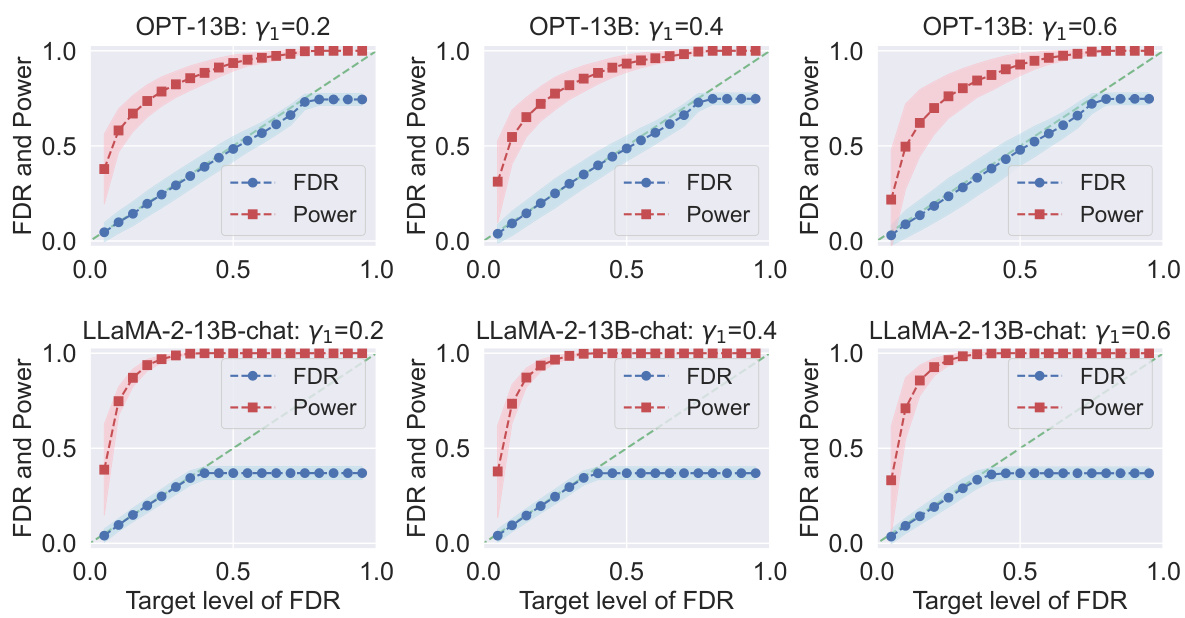
This figure shows the empirical FDR and power of Conformal Alignment for different target FDR levels (x-axis) and different sizes of the reference dataset |D|. It demonstrates the effectiveness of the method in controlling FDR while maintaining relatively high power, especially when |D| is larger. Results are shown for two different language models (OPT-13B and LLaMA-2-13B-chat). The shaded regions represent the standard deviation.
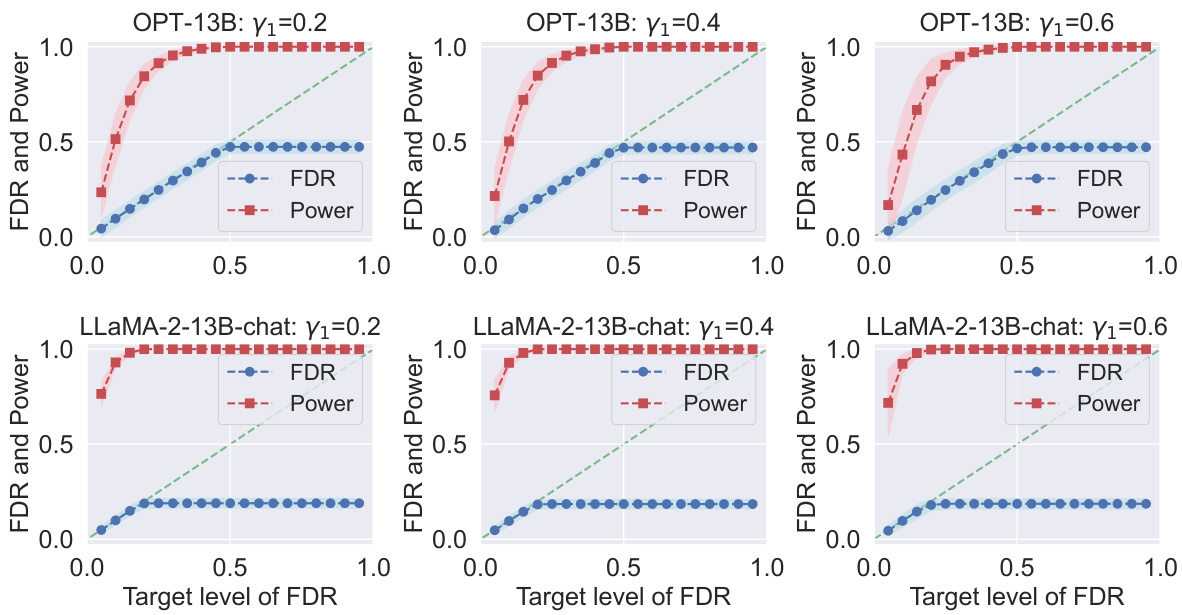
This figure displays the results of applying Conformal Alignment to the TriviaQA dataset for different target FDR levels (False Discovery Rate). It shows the realized (actual) FDR and power (the proportion of correctly selected aligned units) for two different language models (OPT-13B and LLaMa-2-13B-chat) and three different sizes of the reference dataset (|D| = 100, 500, and 2000). The shaded areas represent the standard deviation around the mean, illustrating the variability of the results. The plot demonstrates the effectiveness of Conformal Alignment in controlling FDR while maintaining a reasonable level of power.

This figure displays the results of applying conformal alignment to the TriviaQA dataset. It shows the realized false discovery rate (FDR) and power for different target FDR levels and different sizes of the reference dataset |D|. Separate lines represent the results for two different language models, OPT-13B and LLaMa-2-13B-chat. The shaded regions indicate the standard deviation around the mean values.
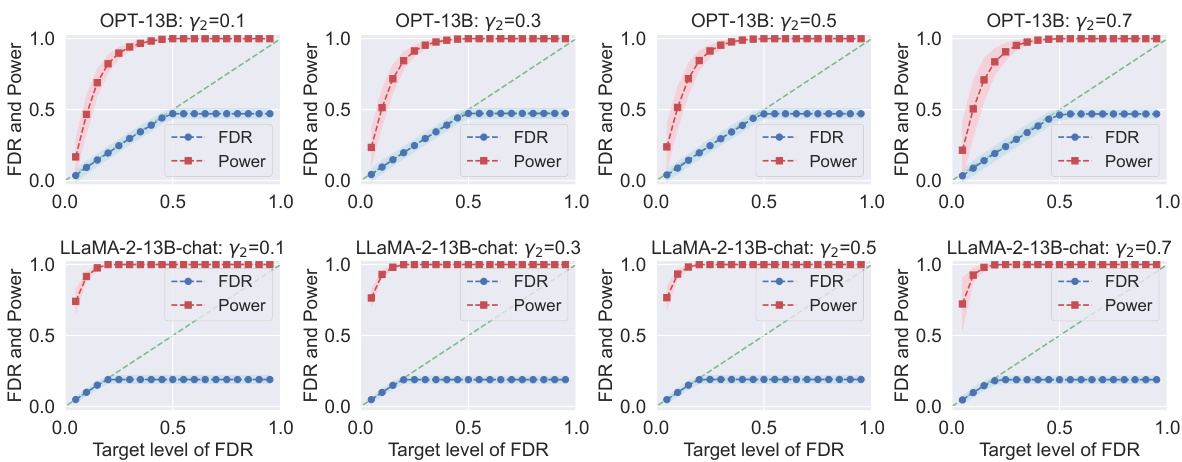
This figure displays the results of applying Conformal Alignment to the TriviaQA dataset for different target FDR levels. It shows both the realized FDR and the power of the method for three different sizes of the reference dataset (|D| = 100, 500, 2000). The top row shows results for the OPT-13B language model, while the bottom row shows results for the LLaMa-2-13B-chat language model. The shading indicates the variability of the results.

This figure visualizes the asymptotic selection rule used in Conformal Alignment. The red dashed line represents the cutoff value for the alignment predictor’s output, g(X). The red curve shows the probability density function of g(X) for units that are not aligned (A < c), while the blue curve shows the probability density function for aligned units (A > c). The area under the blue curve to the right of the cutoff represents the asymptotic power (fraction of truly aligned units selected), and the proportion of the red area to the right of the cutoff to the total area to the right represents the asymptotic false discovery rate (FDR). This illustrates how the method balances selecting as many trustworthy units as possible while maintaining strict control over the FDR.
This figure visualizes the asymptotic selection rule of the Conformal Alignment method. It shows the density curves of the alignment predictor’s output g(X) for units that are truly aligned (A > c, blue curve) and not aligned (A ≤ c, red curve). The red dashed line represents the asymptotic cutoff threshold on g(X) beyond which a unit is selected by the method. The area under the blue curve to the right of the cutoff represents the asymptotic power of the method (proportion of correctly selected units among truly aligned units). The total area under the red curve to the right of the cutoff represents the type-I error (false discovery rate, FDR). The figure illustrates how the method controls the FDR at a pre-specified level by setting the cutoff.

This figure displays the results of applying conformal alignment to the TriviaQA question answering dataset. It shows the achieved false discovery rate (FDR) and power at various target FDR levels (α). Separate results are shown for two different language models, OPT-13B and LLaMa-2-13B-chat. The different columns represent different sizes of the reference dataset (|D|). Shading indicates the standard deviation around the mean for each point.
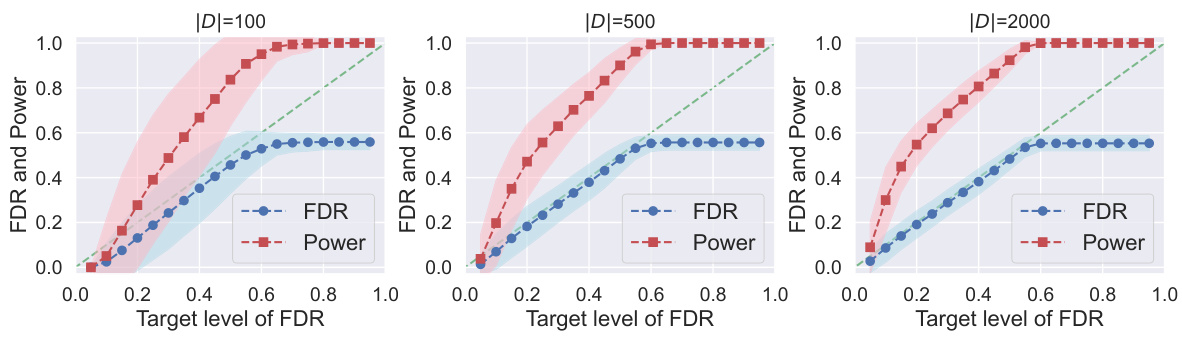
This figure shows the results of applying Conformal Alignment to the TriviaQA dataset for different FDR target levels. It compares the performance of two different language models, OPT-13B and LLaMa-2-13B-chat. Each model’s performance is evaluated across three different sizes of the reference dataset |D| (100, 500, and 2000). The blue line represents the realized False Discovery Rate (FDR), and the red line represents the power of the method. The shaded areas indicate the standard deviation around the mean. The plot shows that the FDR is controlled at the target level for all cases, indicating that Conformal Alignment is effective in selecting units with trustworthy outputs.
This figure visualizes the asymptotic cutoff on the predicted alignment score g(X) beyond which units will be selected by the Conformal Alignment method. The red curve represents the density of g(X) for units with true alignment scores less than the threshold c (A < c), while the blue curve represents the density for units with true alignment scores greater than c (A > c). The red dashed line indicates the asymptotic cutoff, chosen such that the proportion of the red area to the right of the cutoff is less than α (target FDR level). The blue area to the right of the cutoff represents the asymptotic power (the proportion of selected units that are actually aligned).

This figure displays the results of an ablation study investigating the impact of the hyperparameter γ₁ on the performance of conformal alignment. The study focuses on the TriviaQA dataset, with a fixed dataset size |D| of 2000 and γ₂ set to 0.3. Logistic regression is used as the base classifier. The plots show the realized False Discovery Rate (FDR) and power for different target FDR levels, varying γ₁ across three values: 0.2, 0.4, and 0.6. The shaded area represents the standard deviation.
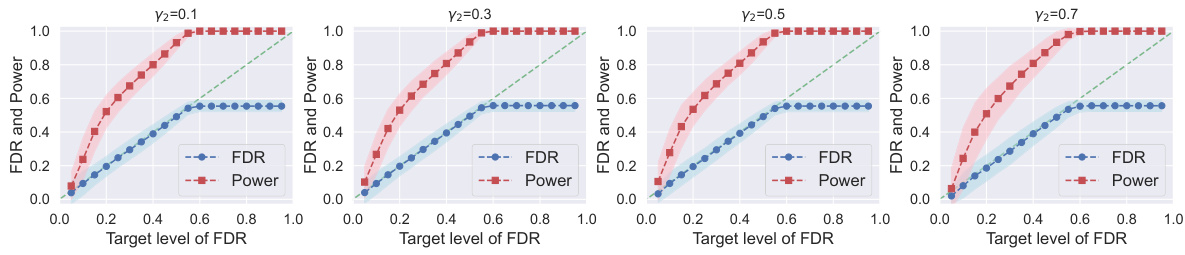
This figure displays FDR and power plots for conformal alignment using the TriviaQA dataset. The experiment varies the proportion (γ₁) of the reference dataset used for hyperparameter tuning, while keeping the total number of high-quality data points constant at |D| = 2000 and using logistic regression as the alignment predictor. The plots show the impact of different γ₁ values on the balance between hyperparameter tuning and model training, affecting the overall FDR control and power of the selection.

This figure shows the results of an ablation study on the choice of hyperparameter γ₁ in the Conformal Alignment algorithm. The study varies γ₁ while keeping the size of the reference dataset |D| and another hyperparameter γ₂ fixed. Logistic regression is used as the base classifier. The plots show the False Discovery Rate (FDR) and power of the algorithm at various target FDR levels. The purpose is to investigate the effect of γ₁ on the algorithm’s performance and determine an optimal value for γ₁.
This figure illustrates the workflow of Conformal Alignment in the context of radiology report generation. It shows how a foundation model generates reports for chest X-rays, and how Conformal Alignment uses a training set and a calibration set to build an alignment predictor. This predictor then assesses the likelihood that each generated report is aligned with human expert reports and selects only those reports exceeding a data-driven threshold, thereby ensuring a controlled false discovery rate (FDR). The pipeline is summarized as ‘Tasks & LLM output’ -> ‘Conformal Alignment’ -> ‘Selective deployment’ -> ‘Reliability Guaranteed!’
Full paper#