Neural Flow Diffusion Models: Learnable Forward Process for Improved Diffusion Modelling

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in generative modeling because it introduces a novel framework, NFDM, that significantly improves diffusion models by allowing for a learnable forward process. This opens up exciting new avenues for research and development in diffusion models, leading to more efficient and flexible models with improved performance across a range of tasks and datasets. The simulation-free optimization of NFDM and its ability to learn generative processes with specific properties further enhances its value to the research community.

Visual Insights

#

This figure compares the trajectories learned by conventional diffusion models (Score SDE) and the proposed NFDM-OT method. The left side shows trajectories from the data distribution, while the right displays those from the prior distribution. NFDM-OT, by learning the forward process, significantly reduces the curvature of the reverse process’s trajectories, leading to more direct paths between the prior and data distributions. This illustrates NFDM-OT’s ability to improve sampling speed and efficiency.

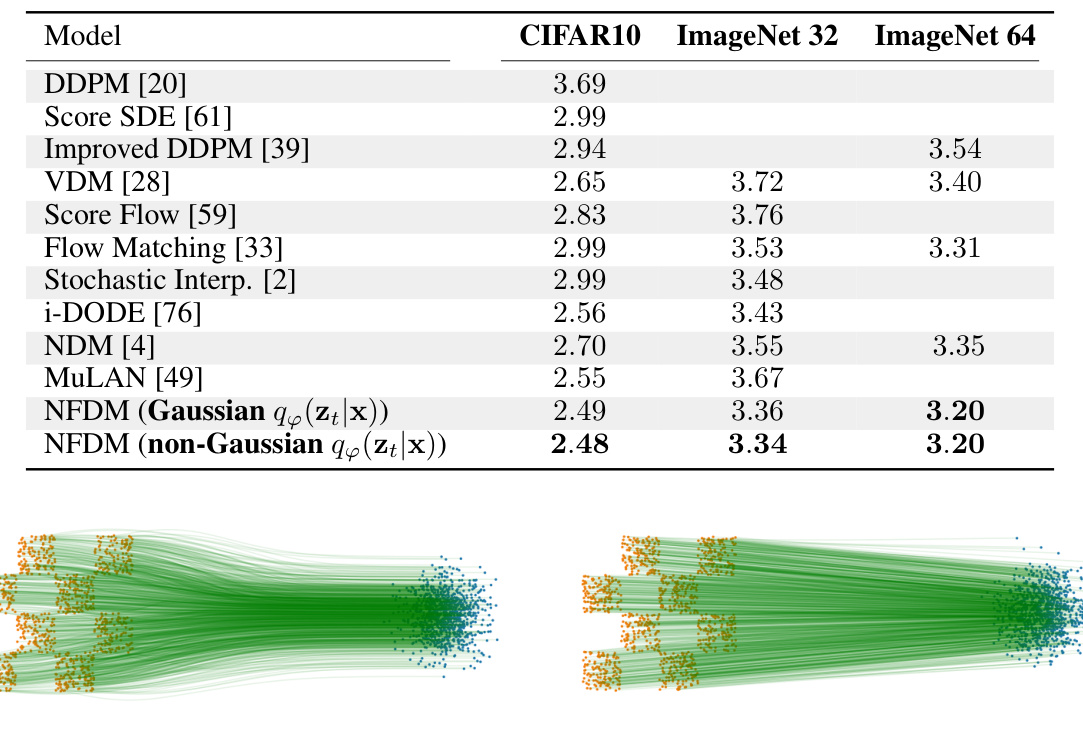
This table compares the bits per dimension (BPD) achieved by NFDM against other state-of-the-art models for density estimation on three benchmark datasets: CIFAR-10, ImageNet 32x32, and ImageNet 64x64. Lower BPD indicates better performance. The results show that NFDM achieves state-of-the-art results across all three datasets.

In-depth insights

#

Learnable Diffusion

#

Learnable diffusion models represent a significant advancement in generative modeling. By learning the forward diffusion process, rather than relying on fixed, pre-defined processes like the standard linear Gaussian, these models gain increased flexibility and control. This allows for the generation of more diverse and higher-quality samples, as the model can adapt to the specific characteristics of the data. Learnable forward processes also offer the potential for improved efficiency in sampling, enabling faster generation of samples and potentially leading to advancements in other areas such as likelihood estimation. However, the introduction of learnable components also brings challenges, such as the need for more sophisticated optimization techniques and increased computational cost during training. Future research will likely focus on developing more efficient methods for learning and optimizing these models and on exploring novel applications enabled by this enhanced control over the diffusion process.

NFDM Framework

#

The NFDM framework presents a novel approach to diffusion models by introducing a learnable forward process. This contrasts with traditional methods that rely on fixed, pre-defined forward processes, often Gaussian. The learnability allows NFDM to adapt to specific data characteristics and simplifies the reverse process’s task, leading to improved likelihoods and sampling efficiency. A key contribution is the simulation-free optimization objective, minimizing a variational upper bound on the negative log-likelihood, making training more efficient. The framework’s flexibility is demonstrated by its ability to learn diverse generative dynamics, including deterministic trajectories and bridges between distributions. However, the framework does impose a restriction on the parameterization of the forward process, limiting the range of applicable distributions. Despite this constraint, NFDM achieves state-of-the-art performance across a range of image generation tasks, showcasing its potential as a versatile and powerful tool for generative modeling.

Bridge Model

#

The concept of a ‘Bridge Model’ in the context of diffusion models is fascinating. It proposes a framework to learn mappings between two distinct data distributions. This is achieved by modifying the forward and reverse processes of a diffusion model, enabling the model to generate samples from one distribution conditioned on samples from another. The key innovation lies in making the forward process learnable and dependent on both source and target distributions, allowing it to effectively bridge the gap. This approach demonstrates the potential for greater flexibility and control over generative processes, extending beyond the limitations of fixed forward processes used in traditional diffusion models. Applications could range from style transfer and image-to-image translation to domain adaptation tasks. The simulation-free training method also allows for efficient optimization, minimizing an upper bound on the negative log-likelihood. A successful bridge model would achieve high-fidelity generation while effectively connecting the two distributions.

Curvature Control

#

Controlling curvature in generative models, especially diffusion models, offers a powerful way to influence the generated samples’ characteristics. By directly manipulating the curvature of the trajectories in the latent space during generation, one can guide the model towards generating smoother or more complex outputs. Lower curvature generally results in more direct and efficient generation, potentially leading to faster sampling speeds. Higher curvature, conversely, allows for exploring more intricate and potentially more varied samples, potentially resulting in increased diversity but possibly at the cost of efficiency. The method of curvature control can involve adding penalty terms to the loss function during training, which penalizes high curvature trajectories. This encourages the model to learn smoother paths, thereby influencing the characteristics of the generated output. The precise mechanism of curvature control is tied to the forward diffusion process; influencing the forward process leads to a corresponding adjustment in the reverse process. Choosing an appropriate curvature control technique requires careful consideration of the trade-off between generation efficiency and the desired level of complexity and diversity in the generated samples. It is important to evaluate the effects of curvature control empirically, assessing its impact on both sampling speed and the quality of the generated samples across different tasks and datasets. The impact on other metrics, like likelihood, also needs to be considered.

Future Works

#

Future work for Neural Flow Diffusion Models (NFDM) could explore several promising directions. Extending NFDM to handle discrete data would significantly broaden its applicability. This would involve developing novel parameterizations and loss functions capable of managing discrete latent variables and outputs. Another area for development is improving the efficiency of the training process, particularly for high-dimensional datasets. Research into more efficient optimization strategies and neural architectures tailored for NFDM is crucial. Further investigation of the impact of different parameterizations of the forward process on the reverse process and overall model performance would lead to more robust and effective models. Exploring the effectiveness of NFDM in various applications, including those beyond image generation (e.g., time series analysis, protein structure prediction), is essential to fully understand its potential. Finally, a detailed theoretical analysis of NFDM’s convergence properties and its relationship to other generative models is needed for a deeper understanding of the model’s capabilities and limitations.

More visual insights

#

More on figures

This figure visualizes the learned stochastic trajectories of Neural Flow Bridge Models (NFBM) trained with an additional penalty to avoid obstacles. The left panel shows the trajectories without obstacles, while the right shows trajectories trained to avoid an obstacle represented by the central circular region. Different colors represent trajectories starting from different initial distributions. The figure demonstrates the NFBM’s capability to learn generative dynamics with specific properties, in this case, obstacle avoidance.

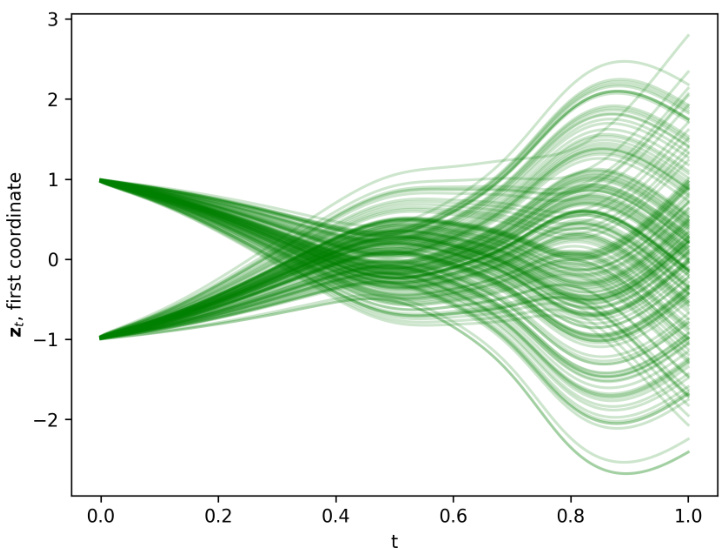
This figure shows the first coordinates of forward deterministic trajectories generated by NFDM-OT. Two starting points, (-1, -1) and (1, 1), are used, and multiple trajectories are plotted to show the variability. The trajectories illustrate the impact of the curvature penalty, which encourages straight-line paths.

This figure shows samples generated from the NFDM model trained on CIFAR-10, ImageNet 32x32, and ImageNet 64x64 datasets. It visually demonstrates the model’s ability to generate images representative of each dataset’s characteristics.

This figure shows samples generated from the NFDM model trained on CIFAR-10, ImageNet 32, and ImageNet 64 datasets. The samples demonstrate the model’s ability to generate high-quality images across different datasets.

This figure visualizes the generative trajectories learned by the Neural Flow Bridge Models (NFBM) when trained on the AFHQ dataset. The NFBM is a modified version of the Neural Flow Diffusion Model (NFDM) designed to learn mappings between two different distributions. In this case, it learns to translate images of dogs into images of cats. The figure shows a sequence of images generated along the trajectory, starting from a dog image at time t=1 and progressing to a cat image at time t=0. Each column represents a different sample, while each row illustrates the transformation at different time steps (t). The smooth transition demonstrates NFBM’s ability to learn a continuous transformation between the two data distributions while avoiding abrupt changes.

More on tables

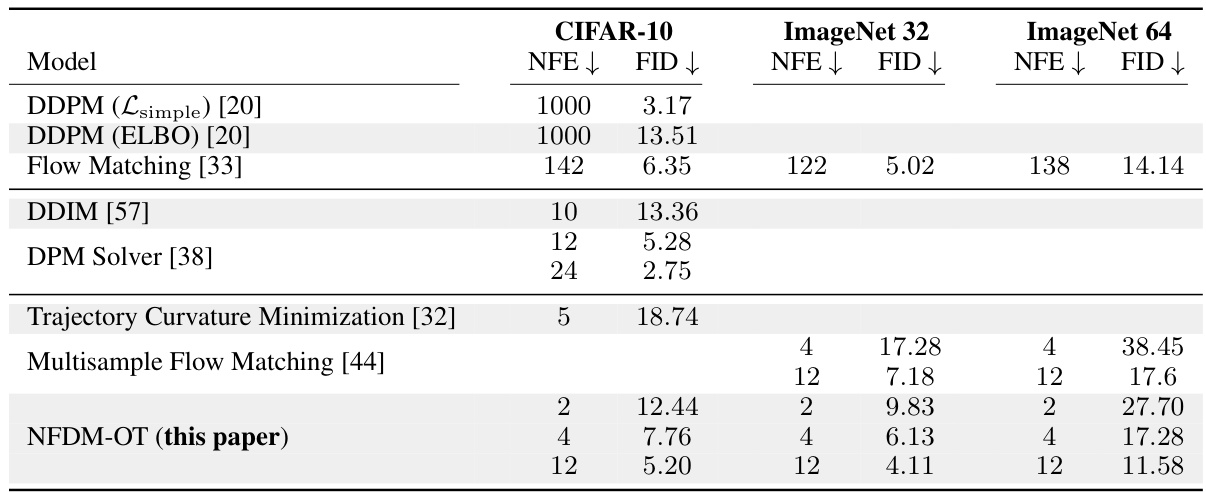
This table compares the Fréchet Inception Distance (FID) scores for different models on image generation tasks with varying numbers of function evaluations (NFE). The table is organized into three sections based on the model’s approach to minimizing curvature. It demonstrates that NFDM-OT achieves better FID scores (indicating higher image quality) compared to baselines with similar NFE values.

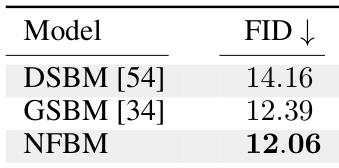
This table presents the Fréchet Inception Distance (FID) scores, a metric for evaluating the quality of generated images, for three different models on the AFHQ 64 dataset, demonstrating the effectiveness of the Neural Flow Bridge Models (NFBM) framework for learning bridges between two distributions.

This table lists the training hyperparameters used in the experiments for different datasets: CIFAR-10, ImageNet 32, ImageNet 64, and AFHQ 64. The hyperparameters include the number of channels, depth of the network, channel multipliers, number of heads, heads channels, attention resolution, dropout rate, effective batch size, number of GPUs used for training, number of epochs, total number of iterations, learning rate, learning rate scheduler (Polynomial or Constant), and the number of warmup steps.

This table compares the performance of the NFDM and NFDM-OT models on density estimation tasks using bits per dimension (BPD) as the metric. Lower BPD values indicate better performance. The table shows that NFDM-OT achieves better results than NFDM, suggesting that penalizing the curvature of the generative trajectories improves performance.

This table summarizes the Fréchet Inception Distance (FID) scores for image generation using different diffusion models with varying numbers of function evaluations (NFEs). It compares models that don’t optimize for trajectory straightness, solvers for pre-trained models, and models specifically designed for minimizing trajectory curvature. The results show that NFDM-OT achieves state-of-the-art performance for a given number of function evaluations.

Full paper

#