↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Boosting is a powerful machine learning technique for combining multiple weak classifiers to create a strong one. However, creating boosting algorithms with optimal sample complexity (the minimum amount of data needed for accurate results) has been challenging. Existing algorithms were either too complex or too slow.
This paper introduces MAJORITY-OF-5, a surprisingly simple algorithm that solves this problem. It partitions the training data, runs AdaBoost on each partition, and then combines the results through majority voting. This algorithm has a provably optimal sample complexity and is faster than existing optimal algorithms.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a surprisingly simple, yet provably optimal, boosting algorithm. Its simplicity and speed, combined with superior empirical performance on large datasets, make it a valuable contribution to the field, potentially replacing slower, existing optimal algorithms. It also opens new avenues for research into the design and analysis of sample-optimal boosting algorithms.
Visual Insights#
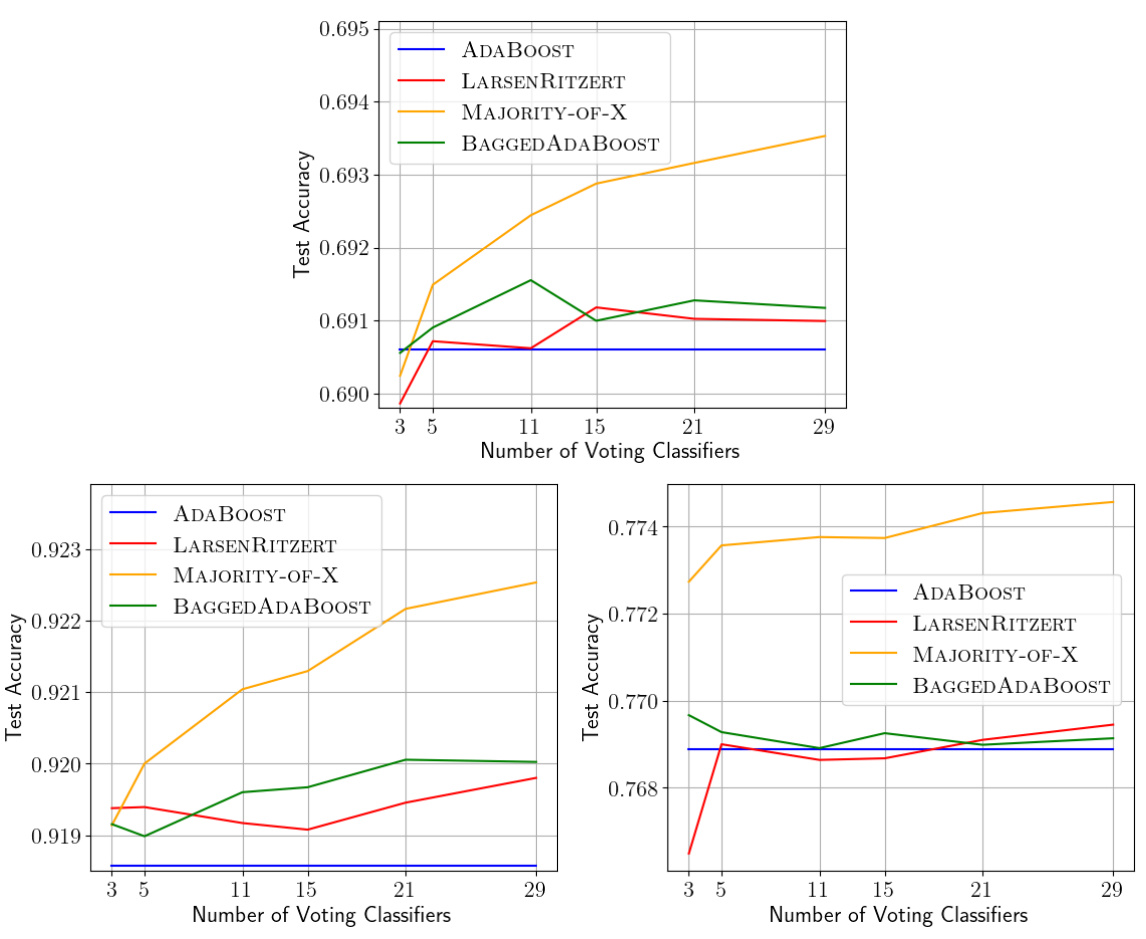
This figure displays the results of experiments comparing the performance of several weak-to-strong learning algorithms on three large datasets: Higgs, Boone, and Forest Cover. Each plot shows the test accuracy of each algorithm as a function of the number of voting classifiers used (3 to 29). The algorithms compared are AdaBoost, LarsenRitzert, Majority-of-X, and BaggedAdaBoost. The x-axis represents the number of voting classifiers, and the y-axis represents the test accuracy.

This figure presents the results of experiments comparing the performance of different sample optimal weak-to-strong learners on three large datasets: Higgs, Boone, and Forest Cover. The x-axis represents the number of voting classifiers used, and the y-axis represents the test accuracy. The plots show the average accuracy across five runs with different random seeds for each algorithm: AdaBoost, LarsenRitzert, MAJORITY-OF-X, and BAGGEDADABOOST. The figure allows for a visual comparison of these algorithms’ performance as the number of classifiers increases.
In-depth insights#
Optimal Boosting#
Optimal boosting algorithms aim to achieve the best possible performance with minimal resources. This is a significant challenge because boosting, while powerful, can be computationally expensive and prone to overfitting. Recent research has focused on developing sample-optimal boosting algorithms, which guarantee optimal performance with a provably minimal number of training samples. This is crucial for datasets where obtaining large amounts of labeled data is expensive or difficult. However, sample optimality is just one aspect of an optimal algorithm. The runtime complexity is equally important. An algorithm might be sample-optimal but computationally impractical. Ideally, an optimal boosting algorithm should be both sample-optimal and computationally efficient, ideally with a runtime comparable to existing boosting methods, like AdaBoost. The practical implications of sample-optimal boosting algorithms are substantial. They could lead to improved generalization performance and reduced overfitting, especially in scenarios with limited data. Furthermore, the development of simpler, provably optimal algorithms might foster a deeper understanding of the fundamental principles behind boosting, possibly leading to new advancements in the field.
MAJORITY-OF-5 Algo#
The MAJORITY-OF-5 algorithm offers a novel approach to weak-to-strong learning, emphasizing simplicity and efficiency. Its core idea is strikingly straightforward: divide the training data into five equal parts, run AdaBoost on each subset, and finally combine the resulting classifiers using a majority vote. This simplicity is a strength, potentially leading to faster runtime and easier implementation than previous optimal algorithms. The algorithm’s provably optimal sample complexity is a significant theoretical contribution, ensuring that it requires a minimal amount of data to achieve high accuracy. Empirical evaluation suggests potential outperformance over existing methods, particularly on large datasets, although further investigation is warranted. The algorithm’s ease of parallelization is also notable, potentially making it highly scalable for massive datasets. However, its performance on smaller datasets may be less compelling, suggesting that it may not be universally superior across all situations. Further research should focus on exploring the algorithm’s behavior in various real-world settings and comparing its practical performance with existing state-of-the-art approaches.
Empirical Study#
The paper’s empirical study is a crucial component, offering a first-ever comparison of recently developed sample-optimal weak-to-strong learning algorithms. It evaluates the performance of these algorithms against the established AdaBoost, using various real-world and synthetic datasets. The results reveal that the new MAJORITY-OF-5 algorithm shows promising performance on larger datasets, potentially outperforming existing methods. Conversely, on smaller datasets, the BAGGING+BOOSTING approach demonstrates superior results. This contrast highlights the importance of dataset size in algorithm selection, suggesting that algorithm performance is highly context-dependent. The empirical study’s findings, while preliminary, lay a strong foundation for future research, emphasizing the need for more extensive comparisons across a broader range of datasets and weak learners to confirm these initial observations and fully understand the strengths and weaknesses of each approach. The careful consideration of dataset size and type is a noteworthy contribution, adding practical relevance to the theoretical advancements presented in the paper.
Runtime Analysis#
A runtime analysis for a boosting algorithm like MAJORITY-OF-5 would focus on the computational cost of its key steps. The dominant factor is likely the number of calls to the weak learner, as it’s invoked multiple times for each subset of data. The algorithm’s simplicity could lead to a relatively low overhead compared to other optimal algorithms. Parallelization opportunities should be explored to reduce the total runtime significantly, as the AdaBoost runs on data subsets are independent. The analysis must consider the trade-offs between the number of subsets and the weak learner’s runtime. Empirical analysis using various data set sizes would be necessary to validate the theoretical runtime complexity and assess the impact of constant factors often hidden in Big O notation. A detailed analysis should quantify the influence of factors like weak learner complexity, data size, and the number of subsets on the overall algorithm performance, perhaps by providing specific runtime estimates or detailed benchmarks. In addition, comparing the runtime of MAJORITY-OF-5 against those of existing algorithms is crucial to highlight the practical advantages of this simple approach.
Future Research#
Future research directions stemming from this work could explore several avenues. Improving the theoretical bounds of MAJORITY-OF-5 is crucial, potentially reducing the number of AdaBoost instances needed below five and enhancing its efficiency. Investigating the impact of different base learners beyond decision trees on the performance of MAJORITY-OF-5 across various datasets warrants further study. A more comprehensive empirical evaluation, including a broader range of datasets and experimental settings (e.g., varying noise levels, class imbalance), is needed to solidify the findings. Exploring parallel implementations of MAJORITY-OF-5 is highly recommended given its inherent parallelizability, evaluating performance scaling on larger datasets. Lastly, understanding the specific characteristics of datasets that make MAJORITY-OF-5 outperform existing algorithms, and developing a more comprehensive theoretical understanding of this phenomenon, is a high priority for future research.
More visual insights#
More on tables

This figure presents the results of experiments comparing different sample optimal weak-to-strong learners on three large datasets: Higgs, Boone, and Forest Cover. The x-axis represents the number of voting classifiers, and the y-axis represents the test accuracy. The figure shows the performance of AdaBoost, LarsenRitzert, Majority-of-X (with X varying), and BaggedAdaBoost. Each algorithm’s performance is averaged over five runs with different random seeds.

This algorithm uses the SUBSAMPLE algorithm as a subroutine to generate a list of training sets. AdaBoost is then run on each training set in the list to obtain a classifier. Finally, the classifiers are combined using a majority vote.

This figure presents the results of experiments comparing the performance of different sample optimal weak-to-strong learners on three large datasets: Higgs, Boone, and Forest Cover. The x-axis represents the number of voting classifiers used, and the y-axis represents the test accuracy. The plots show the average accuracy across 5 runs with different random seeds. The algorithms compared are AdaBoost, LarsenRitzert, Majority-of-X (with X varying from 3 to 29), and BaggedAdaBoost. The figure highlights the relative performance of these algorithms on datasets of differing sizes.
Full paper#