PURE: Prompt Evolution with Graph ODE for Out-of-distribution Fluid Dynamics Modeling

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it tackles the crucial problem of out-of-distribution generalization in fluid dynamics modeling, a significant challenge hindering the real-world application of machine learning in this field. The proposed PURE framework offers a novel solution with strong empirical results, opening avenues for improving the robustness and adaptability of machine learning models in dynamic systems, and potentially impacting various other domains facing similar challenges.

Visual Insights

#

This figure presents a detailed illustration of the PURE (Prompt Evolution with Graph ODE) framework. It shows the different components and their interactions, starting from physical parameters and sensor values as input, and leading to the final prediction output. Key modules, such as multi-view context exploration, time-evolving prompt learning using a graph ODE, and model adaptation with prompt embeddings, are highlighted. The figure also shows the use of attention mechanisms, FFT, and iFFT transforms in the frequency domain, and the integration of the final prompt embeddings into a basic forecasting model for enhanced predictions.

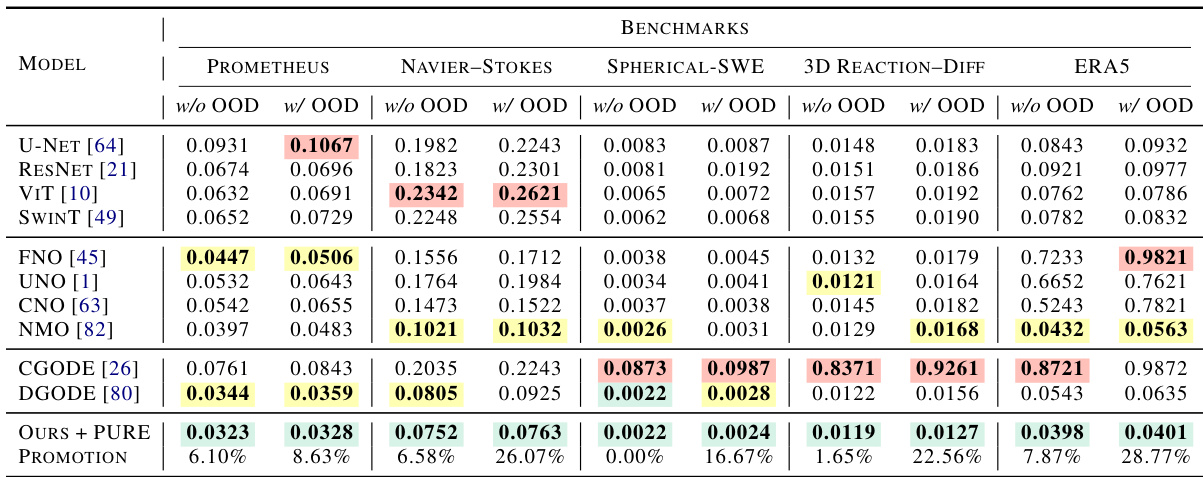
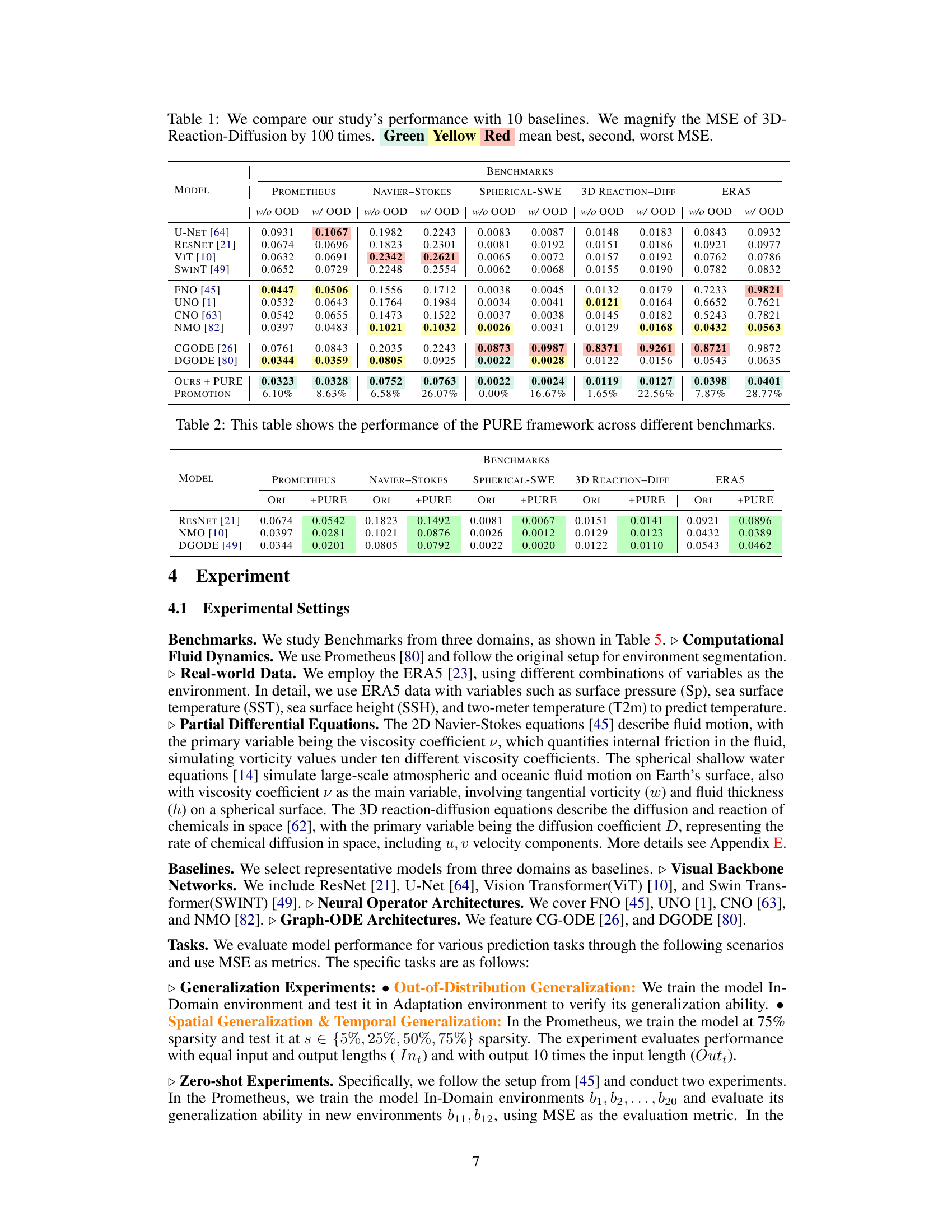
This table presents a comparison of the proposed PURE method against 10 baseline methods across four different benchmarks (Prometheus, Navier-Stokes, Spherical-SWE, 3D Reaction-Diffusion, and ERA5). The Mean Squared Error (MSE) is reported for each method with and without out-of-distribution (OOD) generalization. The MSE for the 3D Reaction-Diffusion benchmark is multiplied by 100 for better visualization. Color-coding (green, yellow, red) highlights the best, second-best, and worst-performing methods, respectively.

In-depth insights

#

Prompt Evolution

#

Prompt evolution, in the context of this research paper, represents a dynamic adaptation strategy for predictive models. Instead of using static prompts, the approach leverages a graph-based ordinary differential equation (ODE) to model the continuous evolution of prompts. This allows the model to adapt to out-of-distribution scenarios by learning time-evolving prompts that capture changes in system parameters and temporal dynamics. The evolution is guided by a graph structure representing the relationships between different elements of the system, and an attention mechanism incorporates the influence of observations in shaping this evolution. This process enhances the model’s robustness and generalizability. The core idea of prompt evolution is to make prompt embeddings a dynamic entity, reflecting the ongoing changes in the environment, rather than relying on fixed, predetermined prompts. This dynamic approach provides a powerful mechanism for enhancing predictive accuracy in complex and evolving systems.

Graph ODE

#

Graph ODEs represent a powerful technique for modeling dynamic systems on graph structures. They elegantly combine the expressive power of graph neural networks with the ability of ordinary differential equations (ODEs) to capture continuous temporal evolution. The key advantage lies in their capacity to learn complex spatiotemporal dependencies, where the graph structure encodes relationships between entities and the ODE governs their temporal dynamics. This approach is particularly effective for systems with irregular or evolving connectivity, which makes it suitable for applications like fluid dynamics modeling. However, challenges exist in training efficiency and scaling to large graphs. The choice of ODE solver, the design of the graph neural network, and the representation of the graph itself all have significant implications for both model accuracy and computational cost. Future work could focus on developing more efficient training algorithms, exploring more sophisticated ODE solvers tailored to graph structures, and expanding the application of graph ODEs to a wider range of complex real-world systems.

OOD Modeling

#

Out-of-distribution (OOD) modeling tackles the challenge of applying machine learning models trained on one data distribution to data drawn from a different distribution. This is particularly crucial in fluid dynamics, where real-world scenarios rarely perfectly match training conditions. PURE, the method discussed, directly addresses OOD modeling by incorporating time-evolving prompts, adapting models dynamically to changes in system parameters or temporal variations. This innovative approach moves beyond traditional assumptions of stationary data distributions, making it more robust and practical for real-world applications. Key to PURE’s success is its capacity to learn invariant observation embeddings alongside time-varying prompts, effectively decoupling environment shifts from core model features. The combination of prompt learning and graph ODEs proves effective in capturing complex spatio-temporal interactions and adapting to diverse OOD scenarios. This focus on capturing both parameter-based shifts and temporal variations offers a superior solution to many existing models.

Fluid Dynamics

#

Fluid dynamics, the study of fluid motion, is a vast and complex field with significant implications across various scientific and engineering disciplines. Computational fluid dynamics (CFD) has emerged as a powerful tool for understanding fluid flow, enabling data-driven modeling where traditional numerical methods fall short, especially when governing equations are unknown or complex. Machine learning approaches offer significant potential for enhancing CFD’s efficiency and accuracy. However, distribution shifts, stemming from varying system parameters and temporal evolution, pose a significant challenge to the reliability of these models. The development of robust and adaptable algorithms, such as those leveraging prompt learning and graph ODEs, is crucial to overcome these limitations and achieve reliable predictions in real-world, out-of-distribution scenarios. The integration of multi-view context information and minimizing mutual information further enhance model robustness. Future research should focus on advancing these techniques to address challenges in complex fluid dynamics and expand applications to diverse fields.

Model Adaptation

#

The heading ‘Model Adaptation’ in a research paper likely discusses how a pre-trained model is adjusted to perform well on a new, unseen dataset or task. This is crucial when dealing with distribution shifts, where training and test data differ significantly. Effective model adaptation techniques often involve fine-tuning the model’s parameters on the new data, transfer learning, where knowledge from a related task is leveraged, or domain adaptation methods to bridge the gap between source and target domains. The paper might explore strategies such as prompt engineering, where carefully designed prompts guide the model’s behavior, or adversarial training, which enhances robustness against distribution shifts. A key aspect is how the adapted model’s performance is evaluated and compared against baselines and other approaches. The discussion might include metrics, visualizations, and analysis of the adaptation process to gain insights into its effectiveness and limitations. Robustness and generalization capabilities are major concerns.

More visual insights

#

More on figures

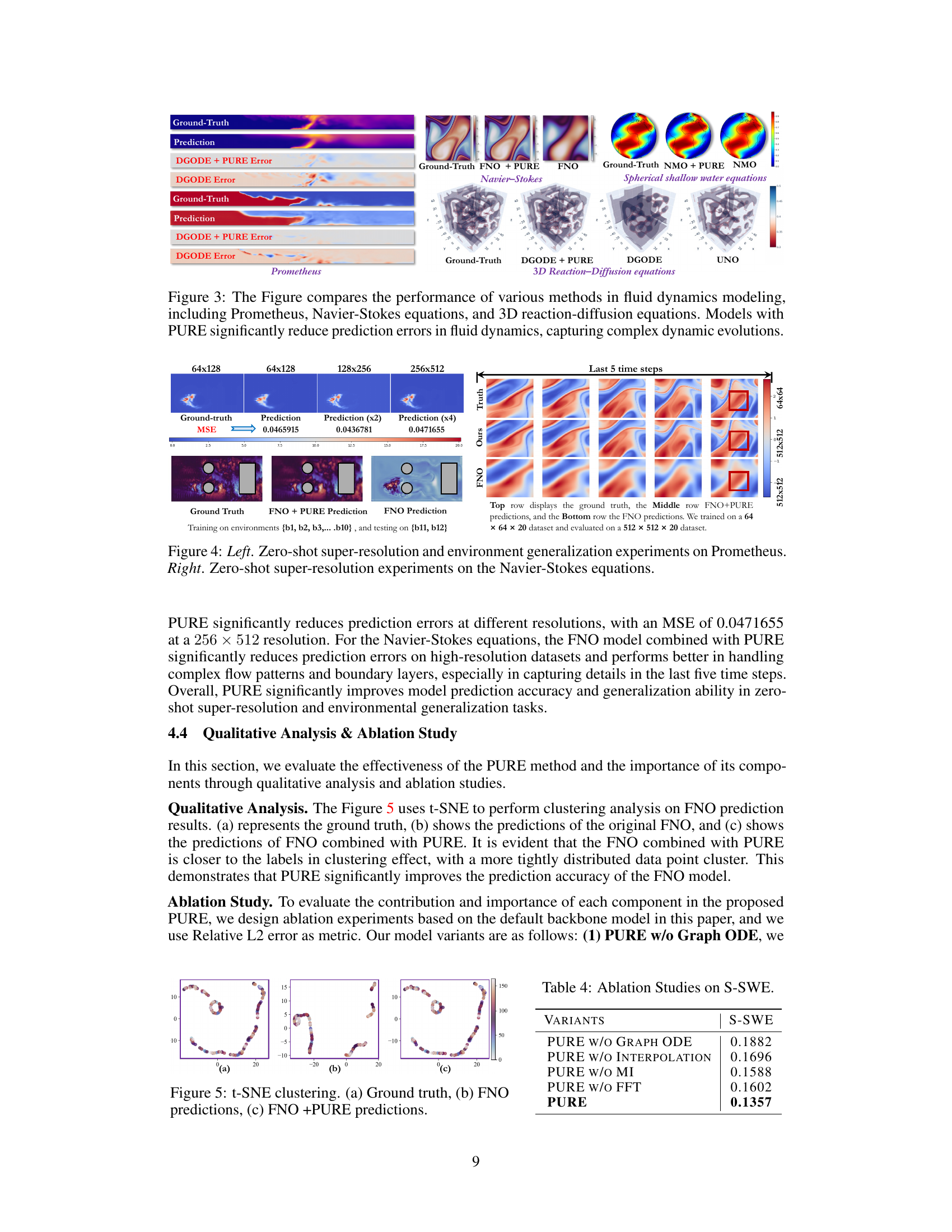
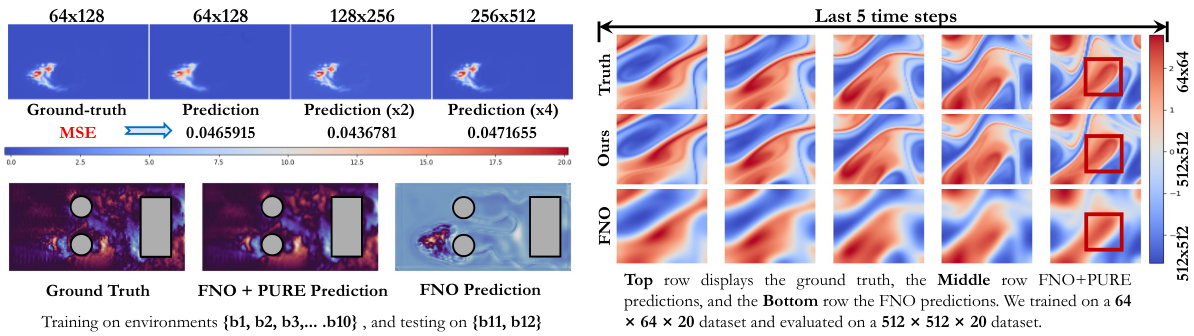
This figure showcases the improved performance of the PURE model compared to other models in various fluid dynamics tasks. It visually presents the ground truth, predictions made by several methods with and without PURE, and the difference between predictions and ground truths for the Prometheus dataset (simulating tunnel and pool fires), 2D Navier-Stokes equations (modeling fluid motion), and 3D reaction-diffusion equations (describing chemical diffusion and reactions). The visual comparisons across different datasets highlight the effectiveness of PURE in enhancing accuracy and capturing complex fluid dynamics details.

This figure presents a detailed overview of the PURE (Prompt Evolution with Graph ODE) framework, which is designed for out-of-distribution fluid dynamics modeling. It illustrates how the framework integrates multiple modules to process spatiotemporal data and system parameters, learn time-evolving prompts using a graph ODE, and adapt basic forecasting models to handle distribution shifts. The diagram visually represents the flow of data through different stages, including initial prompt embedding, multi-view context exploration, time-evolving prompt learning, observation embedding, and model adaptation.

This figure showcases a comparison of different methods used in fluid dynamics modeling across three distinct datasets: Prometheus, Navier-Stokes equations, and 3D reaction-diffusion equations. The comparison highlights the improvements in prediction accuracy and the ability to capture complex dynamic evolutions achieved by incorporating the PURE framework. Visualizations show the ground truth, predictions from different methods (DGODE, FNO, and NMO), and the error differences. The results demonstrate that the PURE method significantly enhances prediction accuracy.

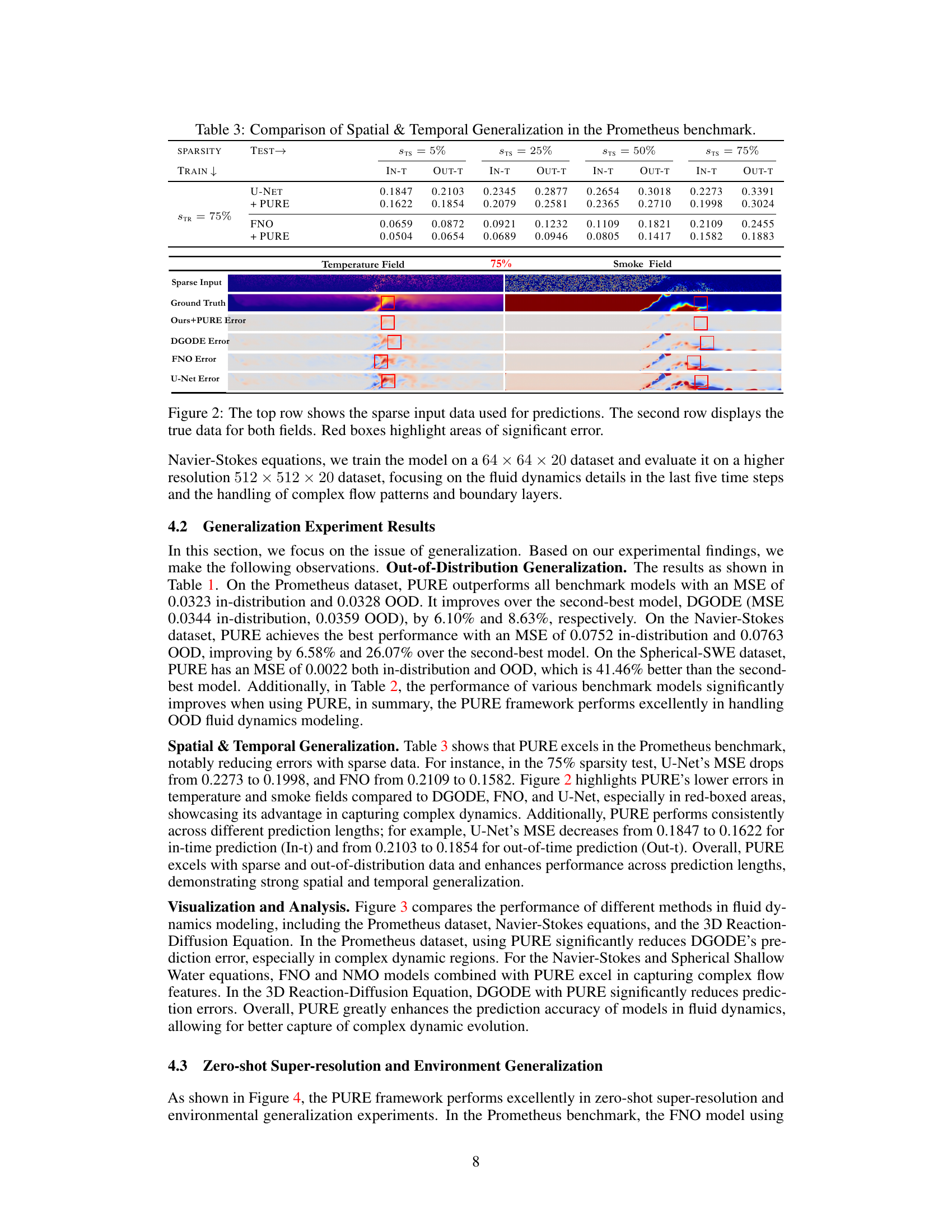
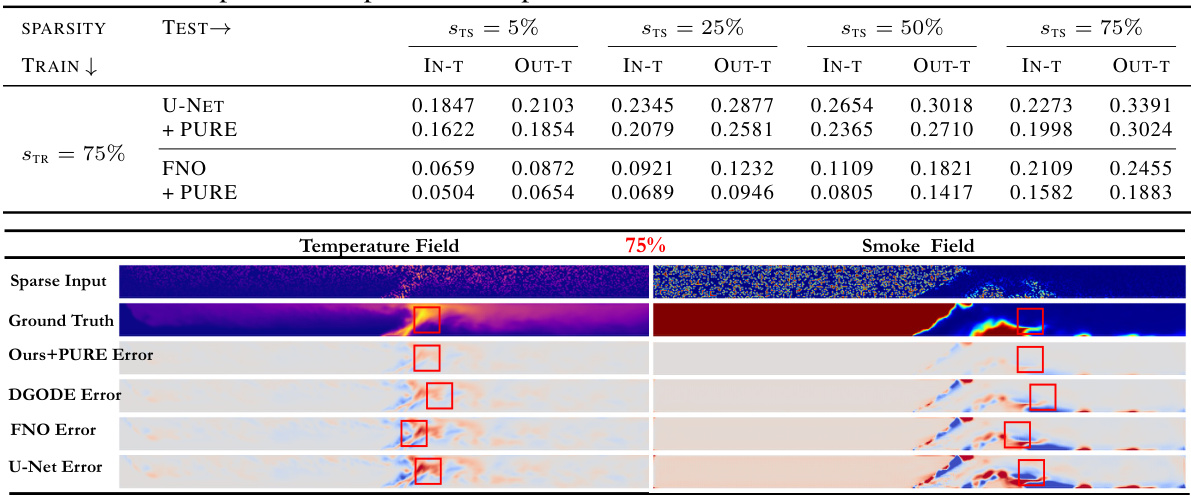
This figure shows a comparison of the sparse input data, ground truth data, and prediction results for both temperature and smoke fields. The top row presents the sparse input data used for prediction. The middle row displays the corresponding ground truth data for both fields. The bottom row presents the prediction errors for the temperature and smoke fields, using our method (Ours) and a baseline method (DGODE), highlighting the areas of significant error in red boxes.

More on tables

This table presents a comparison of the PURE model’s performance against several baseline models across five different benchmark datasets. The datasets cover diverse areas of computational fluid dynamics and real-world data. The ‘ORI’ column shows the baseline model’s performance, while ‘+PURE’ represents the performance improvement achieved by integrating the PURE framework. The results show the mean squared error (MSE) for each model and dataset.

This table compares the performance of the proposed PURE method against 10 baseline methods across four different benchmarks: Prometheus, Navier-Stokes, Spherical SWE, and 3D Reaction-Diffusion. The Mean Squared Error (MSE) is reported for each method with and without out-of-distribution (OOD) generalization. The MSE for the 3D Reaction-Diffusion benchmark is multiplied by 100 for better visualization. The best, second-best, and worst performing methods are highlighted in green, yellow, and red respectively for each benchmark.

This table presents the ablation study results for the Spherical Shallow Water Equation (S-SWE) benchmark. It shows the impact of removing each component of the PURE framework on the model’s performance, measured by the Mean Squared Error (MSE). The variants are PURE without Graph ODE, PURE without Interpolation, PURE without Mutual Information minimization, PURE without FFT, and the complete PURE model. The results demonstrate that all components contribute to the model’s performance.

This table presents a comparison of the proposed PURE method against ten baseline methods across four different benchmarks: Prometheus, Navier-Stokes, Spherical-SWE, and 3D Reaction-Diffusion. The mean squared error (MSE) is reported for each method with and without out-of-distribution (OOD) generalization. The MSE for the 3D Reaction-Diffusion benchmark is multiplied by 100 for better visualization. Green, yellow, and red highlighting indicates the best, second-best, and worst performing methods respectively.

This table presents the ablation study results on the Navier-Stokes equations, evaluating the impact of different components of the PURE framework. By removing each component (Graph ODE, Interpolation, Mutual Information minimization, FFT), the table shows the resulting MSE (Mean Squared Error). This helps to understand the individual contribution of each component to the model’s overall performance. The baseline MSE of the FNO model (without PURE) and the MSE of the complete FNO + PURE model are also included for comparison.

This table presents a comparison of the Mean Squared Error (MSE) achieved by different methods across varying levels of out-of-distribution (OOD) generalization difficulty. The ’easy’, ‘mid’, and ‘hard’ levels likely represent progressively more challenging scenarios where the test data distribution deviates further from the training data distribution. The table allows for a direct comparison of the robustness of different models in handling such distribution shifts.

This table compares the performance of ResNet and NMO models, with and without the PURE framework, under noisy data conditions. The MSE values are reported for both the Prometheus and Navier-Stokes datasets. The results show that the PURE framework significantly reduces the MSE for both models, demonstrating its effectiveness in mitigating the impact of noisy data on the model’s predictive performance.

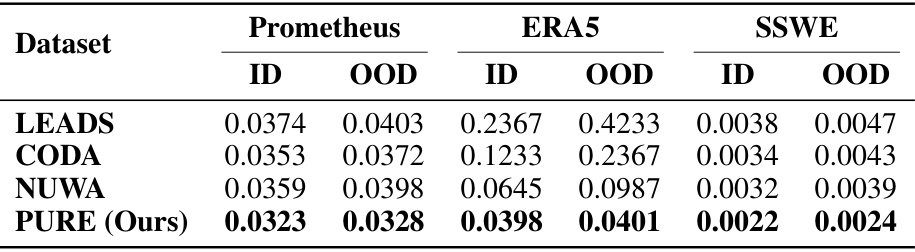
This table compares the performance of the proposed PURE method against other state-of-the-art methods on three different datasets: Prometheus, ERA5, and SSWE. The comparison is made for both in-distribution (ID) and out-of-distribution (OOD) scenarios, using the Mean Squared Error (MSE) as the evaluation metric. Lower MSE values indicate better performance.

Full paper

#