↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating parameters from non-private data is well-studied, with U-statistics being a popular choice in various applications. However, applying this to private data, where individual datapoints’ privacy must be preserved, has been largely ignored. Directly applying existing private mean estimation algorithms to this problem leads to suboptimal results.
This paper focuses on improving private U-statistic estimation. The authors propose a novel thresholding-based approach that leverages local Hájek projections to reweight data subsets. Their new algorithm achieves nearly optimal private error for non-degenerate U-statistics and shows strong evidence of near-optimality for degenerate cases, which greatly improves upon existing methods. This is demonstrated through lower bounds and applications to uniformity testing and sparse network analysis.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and statistics. It addresses the limitations of existing methods for privately estimating U-statistics, offering new algorithms with improved accuracy and efficiency. This work is directly relevant to a wide range of applications, including hypothesis testing and network analysis, opening exciting avenues for future research in privacy-preserving data analysis.
Visual Insights#
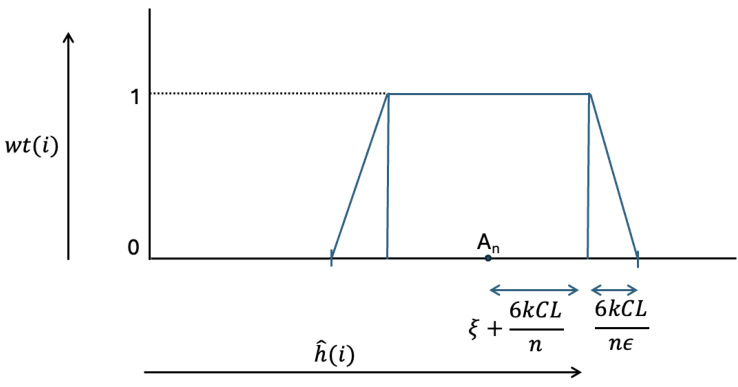
This figure shows the weighting scheme used in equation (14) of the paper. The horizontal axis represents the value of the local Hájek projection ĥ(i) and the vertical axis represents the weight wt(i) assigned to each index i. The weight is 1 for values of ĥ(i) within a certain range around the empirical mean An. As ĥ(i) moves outside this central range, the weight linearly decreases to 0. The intervals where the weight is 1 and the intervals where the weight transitions to 0 are labeled, showing their dependence on the parameters ξ, C, L, and n.

This table compares the private and non-private error rates of different algorithms for estimating U-statistics, including a naive approach, an all-tuples approach, the main algorithm proposed in the paper, and lower bounds for private algorithms. It shows that the main algorithm achieves nearly optimal private error for non-degenerate U-statistics, matching the non-private lower bound (Var(Un)). The table also provides results for bounded, degenerate kernels, indicating near-optimality in that case as well. The comparison highlights the sub-optimality of simpler methods when applied directly to private U-statistic estimation.
Full paper#