↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep learning applications, particularly in reinforcement learning (RL), often involve non-stationary environments. Neural networks must adapt continuously to new information, requiring plasticity. However, many networks suffer from “plasticity loss,” losing their ability to learn effectively over time. This is a major hurdle in several domains where the problem is non-stationary. Existing methods like weight decay attempt to address the issue but can lead to over-regularization or inadequate control of parameter norm growth.
This paper delves into the mechanisms of Layer Normalization (LN), highlighting its ability to revive dormant neurons but also its susceptibility to uncontrolled effective learning rate (ELR) decay. Based on this analysis, the authors introduce Normalize-and-Project (NaP). NaP inserts normalization layers and employs weight projection to maintain constant ELR, providing numerous benefits of normalization while resolving the vanishing gradient issue. Through experiments in various challenging continual learning tasks (sequential supervised learning and a continual variant of Arcade Learning Environment), NaP significantly mitigates plasticity loss and improves performance. Furthermore, the study reveals that the ELR decay caused by parameter norm growth is essential to the success of many deep RL agents. Therefore, it questions the common practice of utilizing constant learning rates in deep RL, suggesting that optimized learning rate schedules could further enhance performance.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical issue of plasticity loss in non-stationary learning environments, a major challenge in deep reinforcement learning and continual learning. By identifying new mechanisms of layer normalization and proposing Normalize-and-Project, it provides valuable insights and practical solutions for improving learning algorithm robustness. The findings challenge common practices and open new avenues for designing more effective learning rate schedules in deep RL.
Visual Insights#

This figure compares the performance of three different network architectures on a continual learning task. The x-axis represents the number of label resets, which means how many times the labels of the training data have been changed. The y-axis of the three subplots represents the final loss, the Jacobian norm, and the parameter norm respectively. The first architecture is a simple feedforward network without normalization, which shows rapid growth in both parameter and Jacobian norms, resulting in poor performance. The second architecture uses layer normalization, which shows reduced Jacobian norm and slower performance degradation but still shows performance decline as parameter norm increases. The third architecture uses layer normalization and weight projection, which is able to maintain the parameter norm at a constant level, resulting in constant performance as good as the initialization. This experiment shows how layer normalization can help to avoid plasticity loss, and how weight projection can help to improve the performance of layer normalization.
This table presents the performance of the proposed method (NaP) on various image classification and language modeling benchmarks. The left side shows the top-1 accuracy on CIFAR-10 and ImageNet-1k, demonstrating that NaP does not hinder performance on standard image classification tasks. The right side displays the per-token accuracy of a large language model (LLM) evaluated on several downstream language tasks. This part showcases that NaP does not negatively impact the performance of LLMs either. Appendix C.5 provides additional results.
In-depth insights#
ELR Dynamics#
The concept of Effective Learning Rate (ELR) dynamics is crucial in understanding the training behavior of neural networks, particularly within the context of normalization layers. ELR is not a fixed parameter but changes dynamically, influenced by factors such as parameter norm growth. In reinforcement learning (RL), where training often occurs on non-stationary problems, controlling ELR dynamics becomes particularly important. The paper highlights how normalization layers implicitly lead to ELR decay due to increasing parameter norms, which can cause loss of plasticity. Explicit control over ELR through methods like Normalize-and-Project (NaP) is thus presented as a crucial mechanism to avoid performance degradation in nonstationary settings. The research demonstrates that the commonly used constant learning rate strategy might be far from optimal, and that carefully designed ELR schedules can significantly improve performance. This necessitates understanding the interplay between normalization, parameter norm growth, and ELR in shaping the optimization landscape.
NaP Protocol#
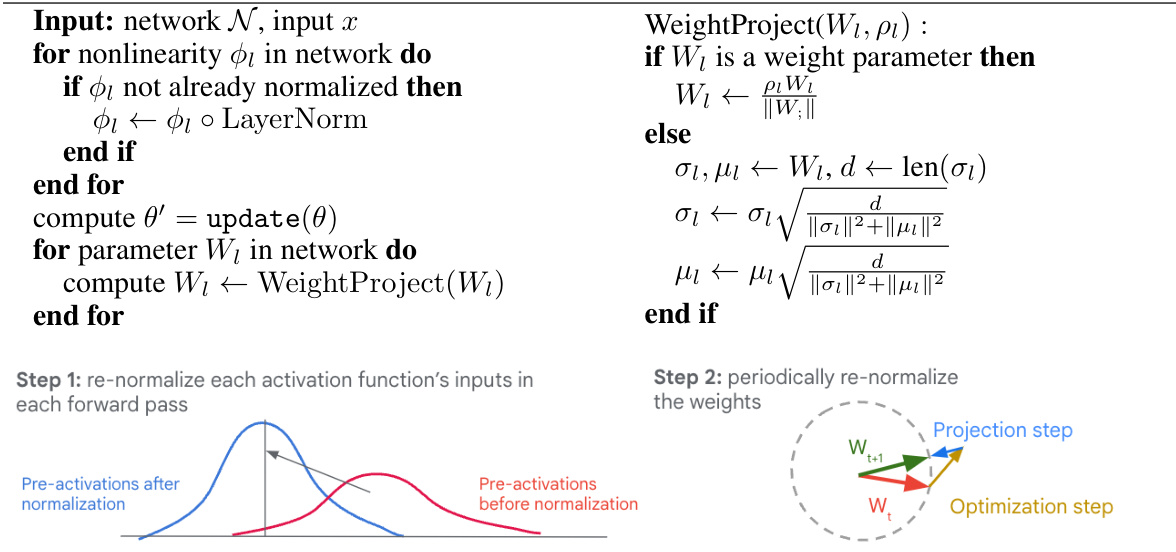
The Normalize-and-Project (NaP) protocol is a novel training approach designed to enhance the stability and plasticity of neural networks, particularly within non-stationary learning environments. NaP combines layer normalization with weight projection, a technique that maintains constant per-layer parameter norms. Layer normalization mitigates the loss of plasticity by preventing the saturation of ReLU units, and it offers resilience against vanishing gradients. Weight projection ensures that the effective learning rate remains constant during training, thus preventing the decay induced by parameter norm growth. This consistent effective learning rate is crucial, as demonstrated in deep reinforcement learning (RL) experiments where an implicit ELR decay is shown to be critical for achieving competitive performance. The effectiveness of NaP is shown across several continual learning scenarios, improving the performance and stability in both supervised and RL settings.
Plasticity Loss#
The concept of “plasticity loss” in neural networks, particularly within the context of continual learning and reinforcement learning, is a critical challenge. Plasticity loss refers to a network’s reduced ability to adapt and learn new information over time, often manifesting as performance degradation on newly encountered tasks or environments. Several factors contribute to this phenomenon including the accumulation of saturated ReLU units, leading to dormant neurons, and the increased sharpness of the loss landscape, making further learning difficult. The implicit decay of effective learning rate (ELR), caused by the growth of parameter norms in models employing normalization layers, is another key mechanism. This loss of plasticity hinders the ability of neural networks to maintain their adaptability in non-stationary settings, demonstrating the importance of developing techniques to mitigate these effects and enhance the robustness of learning algorithms.
ReLU Revival#
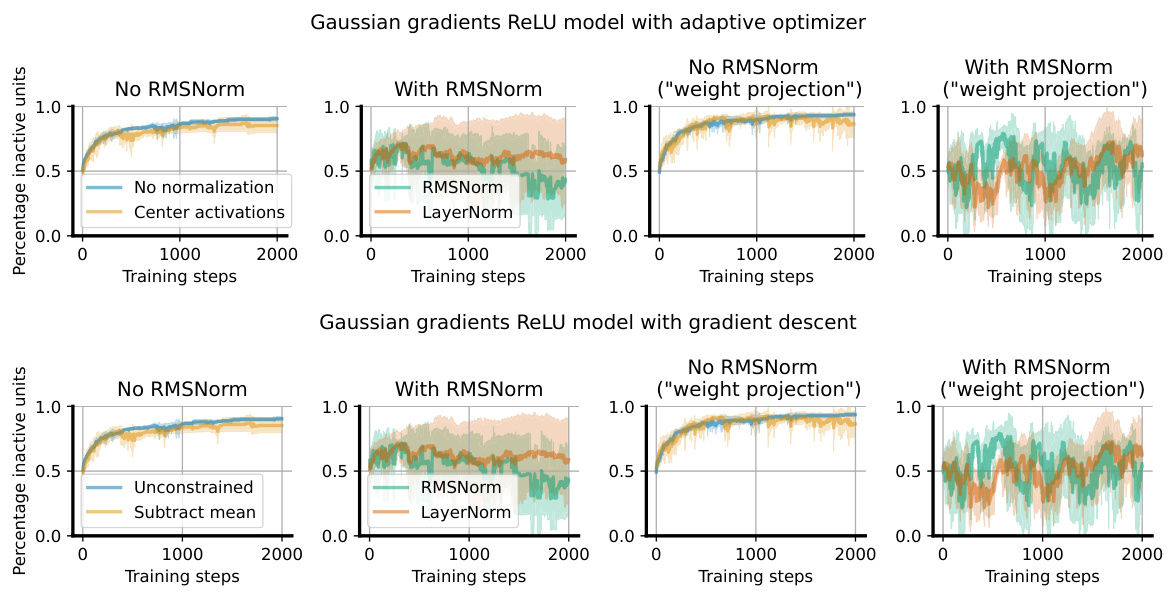
The concept of “ReLU Revival” in the context of neural network training using layer normalization is intriguing. Layer normalization’s ability to counteract the detrimental effects of saturated ReLU units is a key finding. The mechanism appears to be twofold: first, layer normalization effectively ensures that pre-activations maintain a unit variance and zero mean distribution, preventing units from becoming permanently inactive. Second, and perhaps more importantly, layer normalization introduces dependencies between units via mean subtraction and variance normalization. This mixing effect allows for gradient information to still flow to saturated units, even if their direct gradients are zero, thereby allowing them to “revive” or become active again. This is particularly significant in non-stationary environments, where units can become dormant due to concept drift. The revival mechanism is a critical aspect of layer normalization’s effectiveness at preserving network plasticity.
Deep RL Impact#
Deep reinforcement learning (RL) presents a transformative potential across diverse sectors. Game playing showcases its prowess, achieving superhuman performance in complex games like Go and StarCraft. Robotics benefits from its ability to learn intricate motor skills and adapt to dynamic environments, leading to more agile and versatile robots. In healthcare, Deep RL optimizes treatment plans, accelerates drug discovery, and enhances personalized medicine. However, challenges remain. Sample efficiency needs improvement to reduce training time and data requirements. Safety and robustness are crucial, particularly in safety-critical applications, requiring rigorous testing and mitigation strategies. Explainability and interpretability are also needed for increased trust and wider adoption. Bias and fairness must be addressed to prevent discriminatory outcomes. Despite these challenges, the long-term impact of Deep RL is likely to be significant, promising advancements in numerous domains.
More visual insights#
More on figures
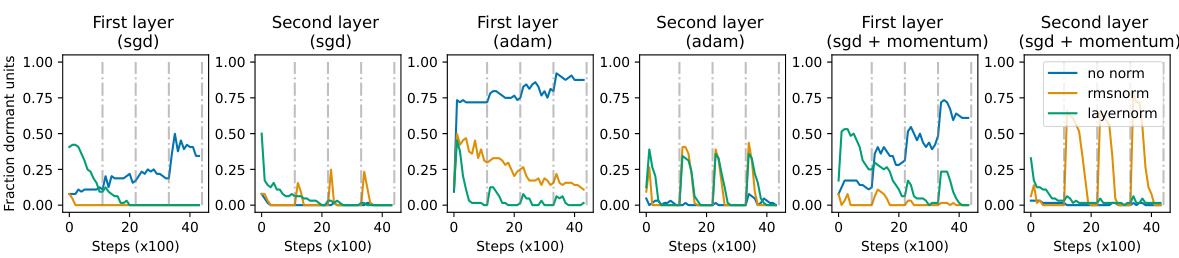
The figure shows the fraction of dormant ReLU units over training steps for different optimizers (SGD, Adam, SGD with momentum) and normalization methods (no normalization, RMSNorm, LayerNorm). The task is continual learning where the MNIST labels are randomly reassigned every 1000 steps. The plot shows that networks using normalization layers (RMSNorm and LayerNorm) are less susceptible to accumulating dead units compared to networks without normalization, indicating normalization’s ability to help networks recover from periods of low plasticity.

This figure compares the learning curves of four different network training setups. All networks are trained on the same task. The first three subplots show layer-wise rescaling with NaP, global rescaling, and no rescaling of the learning rates. The last subplot combines all three into one graph. The key finding is that while a global learning rate schedule produces very similar results to the NaP approach, perfectly matching the dynamics requires layer-wise rescaling.

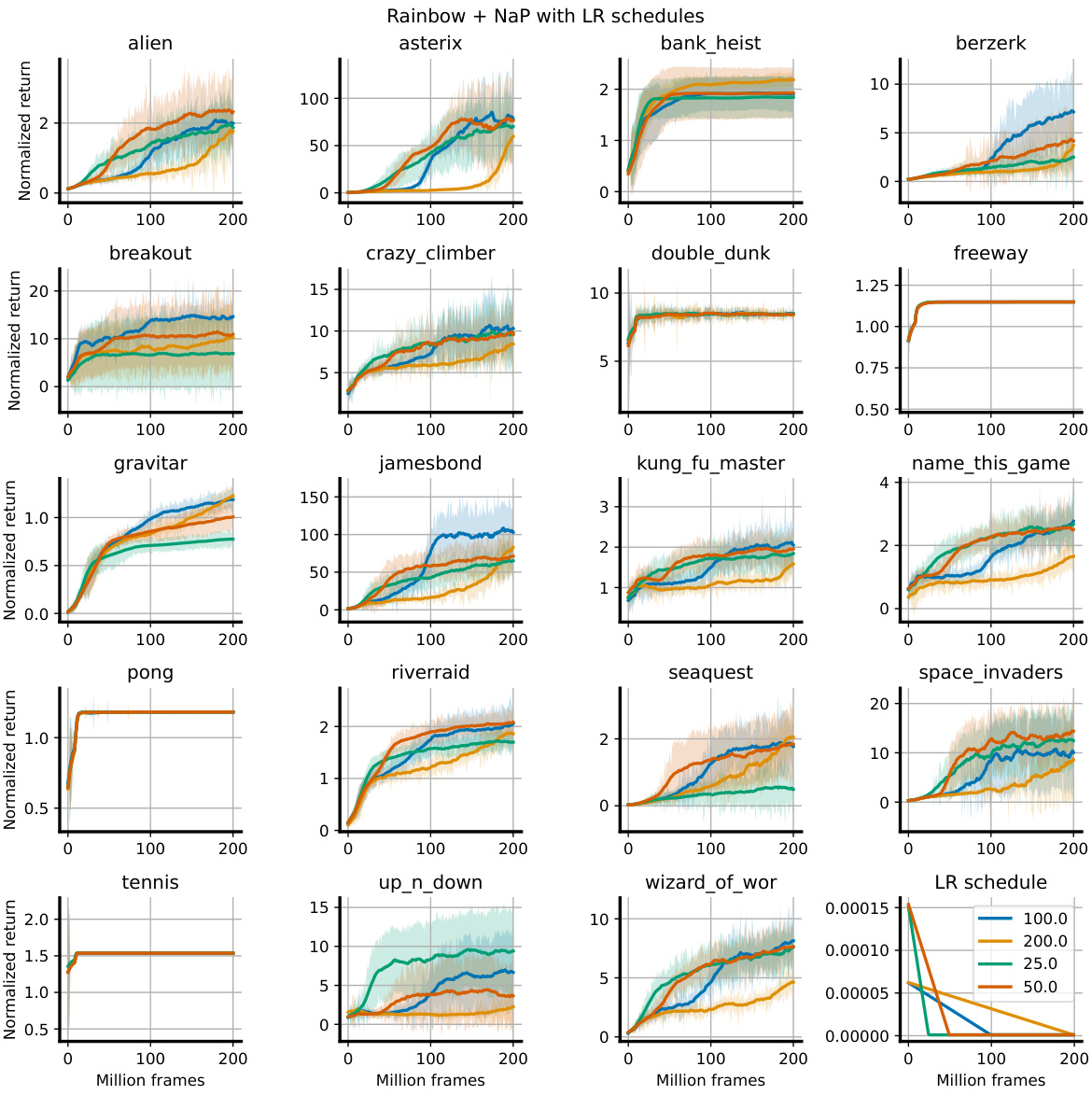
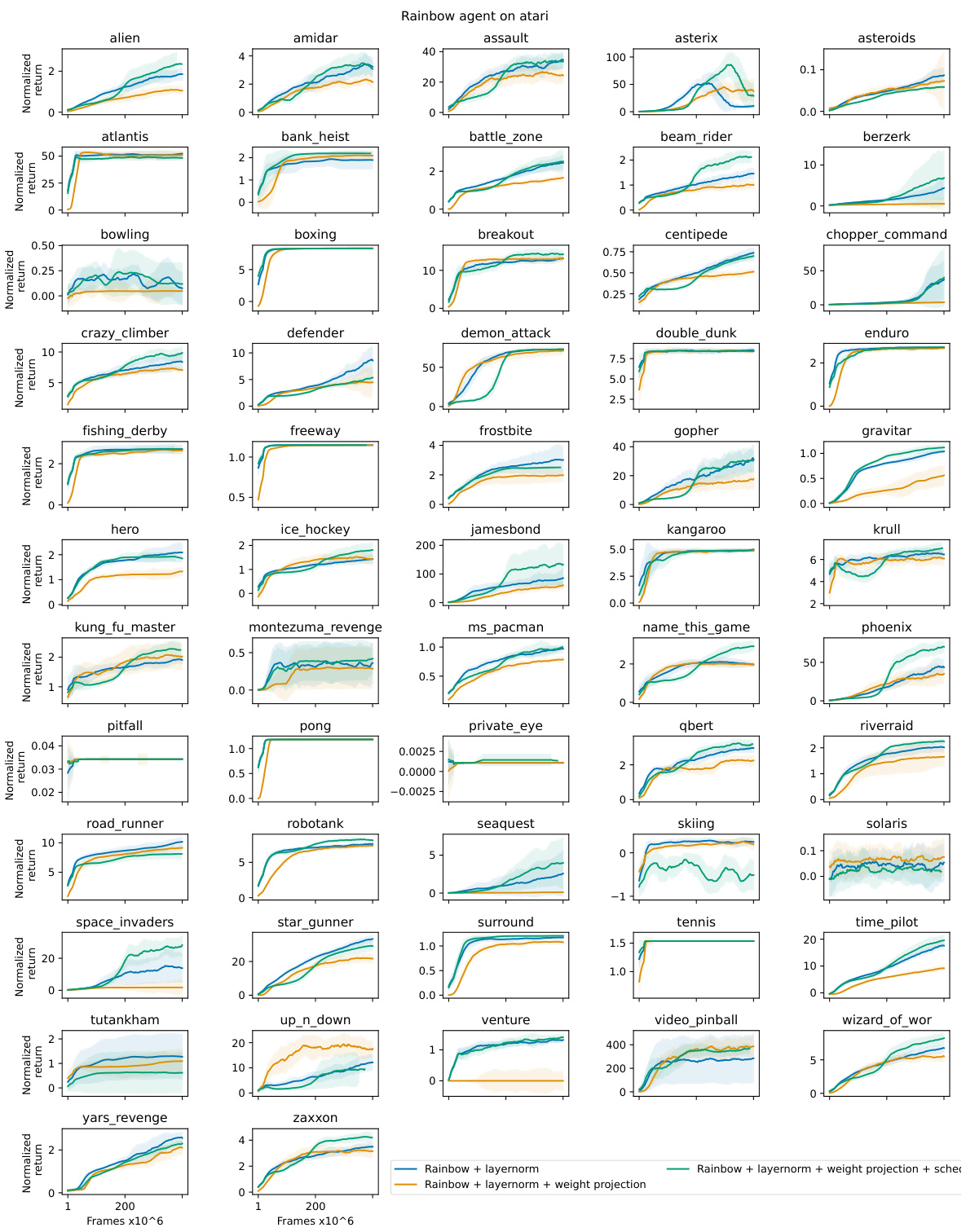
This figure shows the normalized return of Rainbow agents trained on five different Atari games with different training protocols. The x-axis represents the training progress in millions of frames, and the y-axis represents the normalized return. The different lines represent different training protocols: Rainbow + LN (layer normalization), Rainbow + LN + WP (layer normalization and weight projection), and LN + WP + Schedule (layer normalization, weight projection, and learning rate schedule). The figure demonstrates that the implicit learning rate schedule in Rainbow agents is important for performance but not optimal; using an explicit learning rate schedule can significantly improve performance.
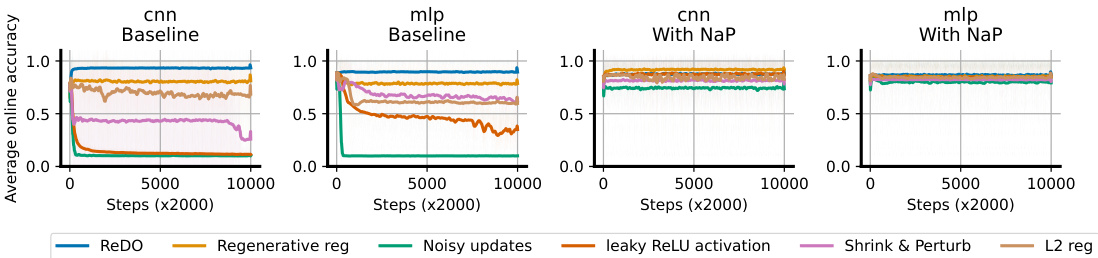
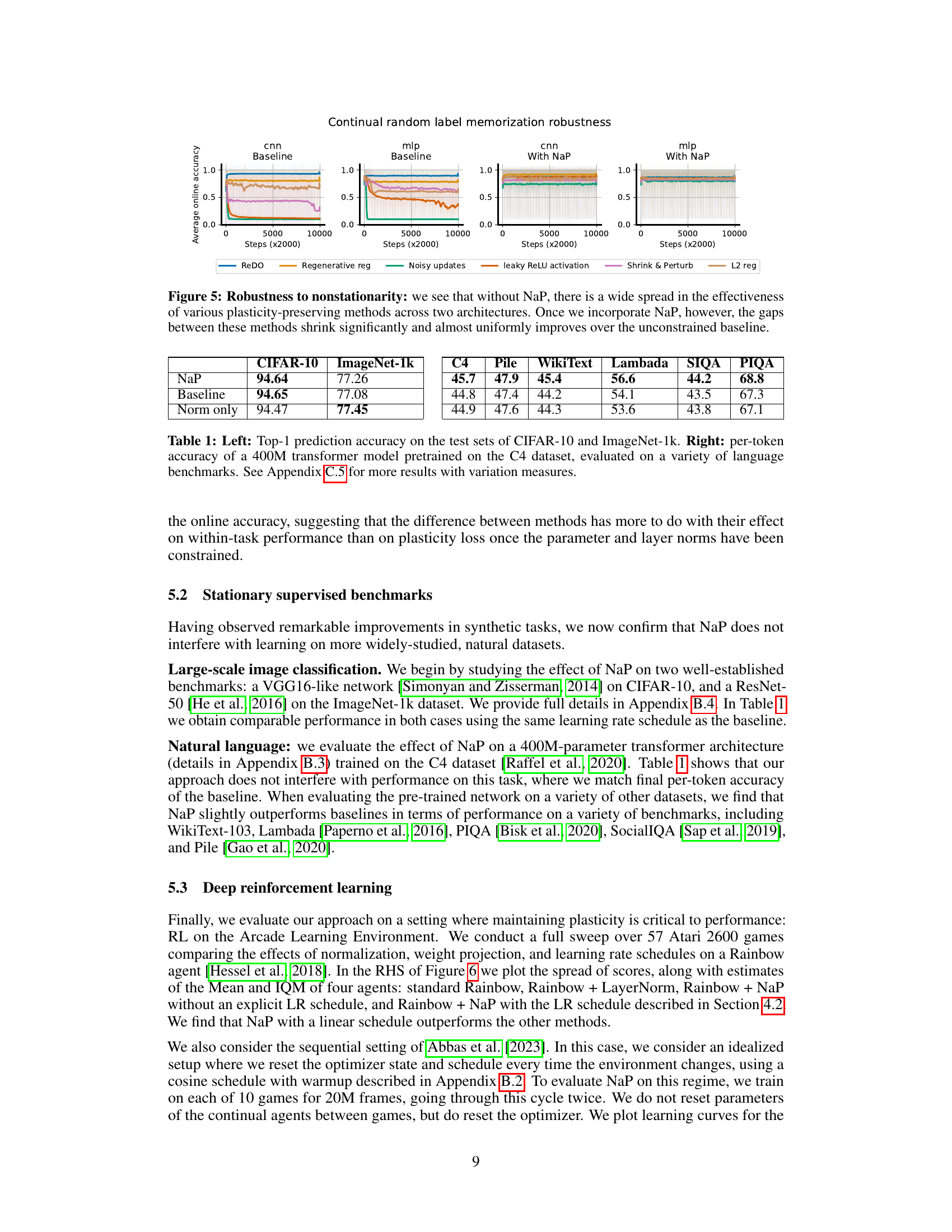
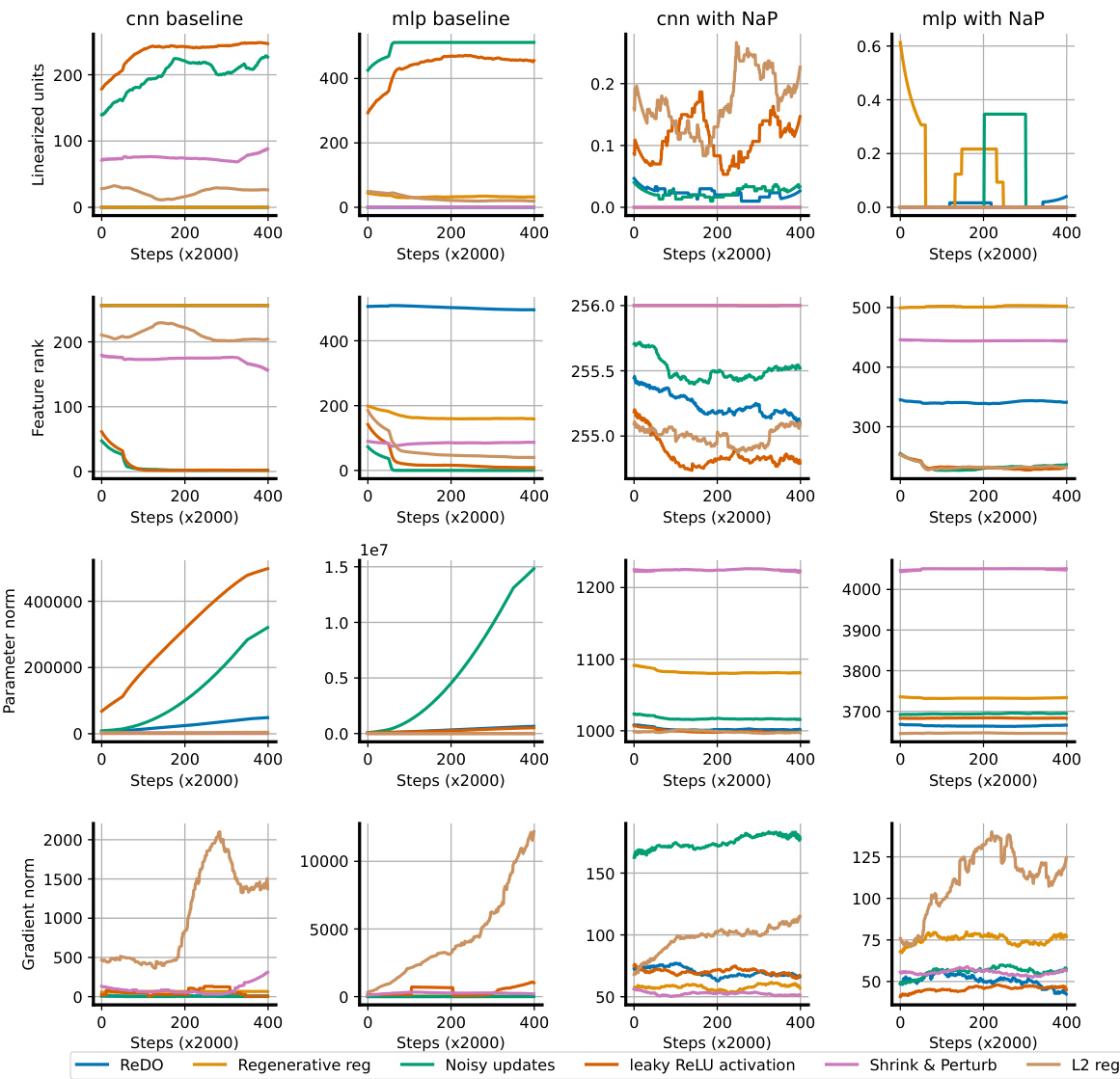
The figure shows the average online accuracy of different plasticity-preserving methods (ReDO, Regenerative regularization, Noisy updates, leaky ReLU activation, Shrink & Perturb, and L2 reg) on a continual random label memorization task using two architectures (CNN and MLP). The left two panels show the performance of these methods without using the proposed Normalize-and-Project (NaP) method. The right two panels show the performance of the same methods when NaP is used. The results demonstrate that while there’s a large variation in performance among the methods without NaP, the introduction of NaP dramatically reduces this variation and improves overall performance across all methods.
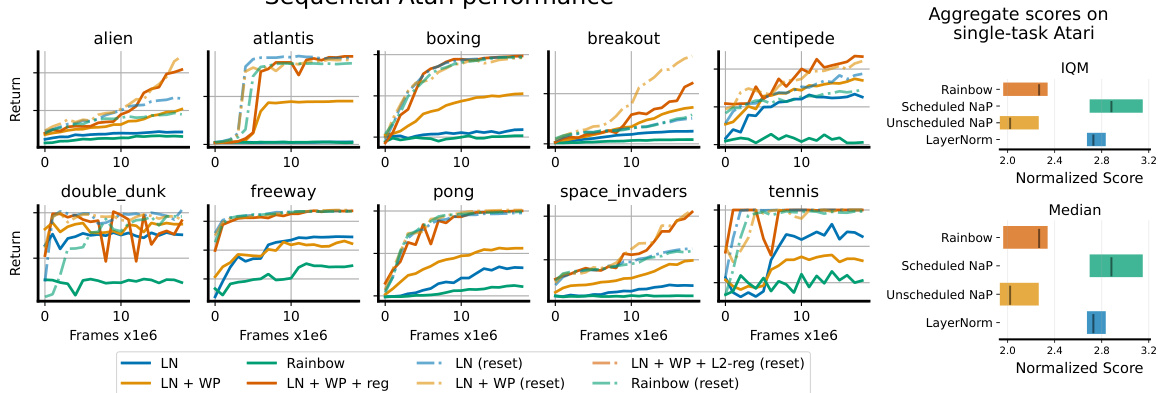
The left panel of Figure 6 shows learning curves for continual learning on Atari games. Ten games were played sequentially, each for 20M frames and repeated twice for a total of 400M frames. The results demonstrate that NaP maintains plasticity, showing performance comparable to a randomly initialized network even on repeated games, unlike a standard Rainbow agent. The right panel provides a summary of the results from single-task Atari experiments, showing the improvement of NaP in terms of median and interquartile mean scores.
This figure shows the fraction of dormant ReLU units over training steps for a network trained on an iterated random label memorization task using different optimizers (SGD, Adam, SGD+momentum) and normalization techniques (no normalization, RMSNorm, LayerNorm). The task involves re-randomizing the MNIST dataset labels every 1000 steps, creating non-stationarity. The plot demonstrates that networks employing layer normalization (LayerNorm) exhibit better resilience against spikes in the number of dead units compared to networks without normalization. The results suggest that LayerNorm helps recover from the temporary deactivation of ReLU units caused by the non-stationary nature of the task.
This figure shows the fraction of dead ReLU units over training steps for different optimizers (SGD, Adam, SGD with momentum) and normalization methods (no normalization, RMSNorm, LayerNorm). The task is continual learning where the MNIST labels are re-randomized every 1000 steps. The key observation is that networks with normalization layers (RMSNorm, LayerNorm) show a significantly reduced number of dead units compared to networks without normalization, demonstrating their ability to recover from periods of high unit saturation.
This figure visualizes the accumulation of dead ReLU units during an iterated random label memorization task on the MNIST dataset. The labels are randomly reassigned every 1000 optimization steps, simulating a non-stationary environment. The plot compares the fraction of dormant units over training steps for networks with different normalization layers (LayerNorm, RMSNorm) and a network without normalization. It demonstrates that networks incorporating normalization layers are more resilient to the spikes in dead unit counts caused by the label changes, showcasing their ability to recover plasticity.
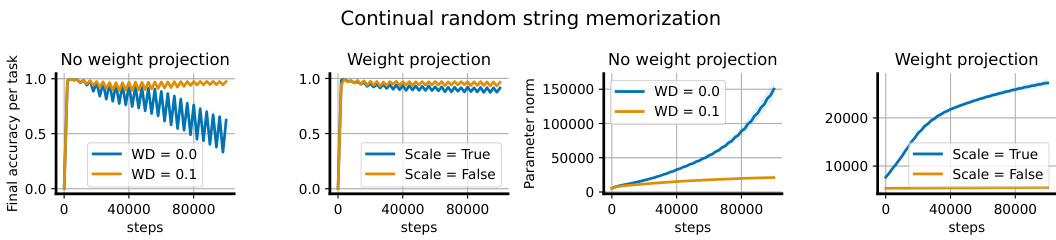
The figure shows the results of experiments on a continual classification problem where the labels of an image dataset are re-randomized iteratively. Multiple plasticity-preserving methods were evaluated on two architectures, a CNN and an MLP, both with and without the Normalize-and-Project (NaP) method. Without NaP, the performance of these methods varied significantly. However, with NaP, the performance gaps between these methods reduced substantially, and NaP consistently improved over the baseline without any plasticity-preserving methods.
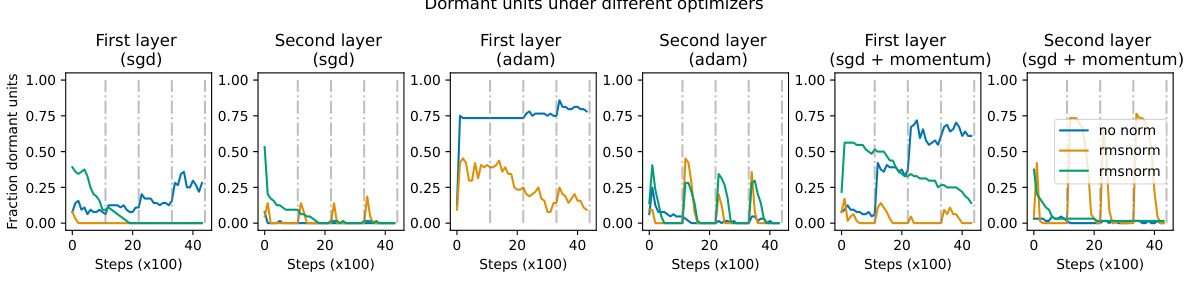
This figure shows the fraction of dormant units (ReLU units that are always zero) over training steps for a network trained on a task where the labels are re-randomized every 1000 steps. The different lines represent different normalization methods (no normalization, RMSNorm, LayerNorm). The key observation is that networks using normalization layers (RMSNorm and LayerNorm) are much more resilient to increases in the number of dormant units and are able to recover from periods where many units become dormant.
This figure shows the fraction of ‘dead’ ReLU units over training steps in a network trained on a task where labels are re-randomized every 1000 steps. Different optimizers (SGD, Adam, SGD with momentum) and normalization methods (no normalization, RMSNorm, LayerNorm) are compared. The results indicate that networks with normalization layers are more resilient to spikes in the number of dead units and can recover more effectively.

This figure shows the results of training a simple feedforward network and a similar network with layer normalization on a continual learning task using CIFAR-10 with randomly relabeled data. It illustrates that the network without normalization shows significant growth in both parameter norm and gradient norm, resulting in decreased performance over time. Conversely, the normalized network shows parameter norm growth but with reduced gradient norm, still experiencing a performance drop but less severe than the non-normalized network. Finally, constraining the parameter norm in the normalized network maintains performance close to the initial random initialization.

This figure shows the results of an experiment on a simple MLP model designed to memorize randomly assigned labels to MNIST digits. The labels are re-randomized every 1000 steps. Different optimizers (SGD, Adam, SGD+momentum) are used with and without layer normalization (layernorm, rmsnorm). The plot shows the fraction of ‘dead’ ReLU units (units that are always 0) over the course of training. It demonstrates that layer normalization helps the network recover more quickly from spikes in the number of dead units, showcasing its ability to revive dormant neurons.
This figure shows the fraction of dormant ReLU units over training steps for a network trained on an iterated random label memorization task. In this task, the network is trained to memorize random labels of MNIST, which are then re-randomized every 1000 steps. The results are shown for networks with different types of normalization layers (no normalization, RMSNorm, LayerNorm) and optimizers (SGD, Adam, SGD+momentum). The figure demonstrates that networks with normalization layers are better able to recover from spikes in the number of dead units that can occur during training on non-stationary tasks.
More on tables

This table presents the results of experiments evaluating the proposed method (NaP) on image classification and language modeling benchmarks. The left side shows the top-1 accuracy on CIFAR-10 and ImageNet-1k image classification tasks. The right side displays the per-token accuracy on various language modeling benchmarks (C4 Pile, WikiText, Lambada, SIQA, PIQA) using a large transformer model pre-trained on the C4 dataset. The baseline and a version using only normalization are included for comparison. Appendix C.5 contains additional results and variation measures for a more complete comparison.

This table presents the results of experiments conducted on image classification and language modeling tasks to evaluate the performance of the proposed Normalize-and-Project (NaP) method. The left side shows the top-1 prediction accuracy on the CIFAR-10 and ImageNet-1k datasets, comparing NaP against a baseline and a model using only normalization. The right side presents the per-token accuracy of a large language model on various benchmarks, also comparing NaP against a baseline. Appendix C.5 provides additional results and variations.

This table presents the results of applying the Normalize-and-Project (NaP) method to image classification and natural language processing tasks. The left side shows the top-1 prediction accuracy on the CIFAR-10 and ImageNet-1k datasets, comparing NaP’s performance to a baseline and a version using only normalization. The right side displays the per-token accuracy of a large language model (400M parameters) trained on the C4 dataset and evaluated on various language benchmarks (Pile, WikiText, Lambada, SIQA, PIQA). The results demonstrate that NaP does not negatively impact performance on these standard tasks.
Full paper#