Bridging Geometric States via Geometric Diffusion Bridge

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in materials science, quantum chemistry, and related fields. It provides a novel and efficient method for bridging geometric states, improving accuracy and applicability in various scientific challenges. The introduction of the Geometric Diffusion Bridge (GDB) framework opens new pathways for modeling complex systems, enabling more accurate predictions and deeper understanding of their evolution dynamics. Furthermore, the scalable and simulation-free training method significantly reduces computational costs, making it accessible to a wider range of researchers.

Visual Insights

#

The figure presents the training algorithms for the Geometric Diffusion Bridge (GDB) framework. Algorithm 1 outlines the training process when only initial and target states are available, while Algorithm 2 extends this to incorporate trajectory data, improving the accuracy and detail of the geometric state evolution modeling. Both algorithms leverage a parameterized model, vθ, to estimate the score of a diffusion process, aiming to accurately capture the dynamics and dependencies between states. The objective function in both algorithms aims to minimize the difference between the estimated score and the true score of the transition density.

The table compares various approaches for bridging geometric states, highlighting their capabilities in handling symmetry constraints, preserving coupling between initial and target states, and utilizing trajectory guidance. It shows that existing methods like direct prediction and MLFFs each address certain aspects but lack the comprehensive capabilities of the proposed Geometric Diffusion Bridge (GDB).

In-depth insights

#

Geometric State Bridge

#

The concept of a “Geometric State Bridge” in a research paper likely refers to a method or framework for modeling and predicting the evolution of geometric states in complex systems. This could involve techniques to bridge the gap between initial and final geometric configurations, potentially leveraging intermediate states or trajectory data to improve accuracy and understanding of the underlying dynamics. The approach might incorporate probabilistic methods, such as diffusion models, to capture the uncertainty inherent in such evolutions. A key aspect could be the preservation of symmetry constraints often present in geometric systems (e.g., rotational or translational invariance). The successful implementation of a Geometric State Bridge would offer a powerful tool for tackling challenges in various scientific domains where accurate prediction of geometric state evolution is crucial, such as molecular dynamics and materials science. The efficacy and generality of such a bridge would depend on its ability to handle complex systems, account for uncertainties, and maintain essential symmetries.

Equivariant Diffusion

#

Equivariant diffusion bridges the gap between traditional generative models and the need for symmetry preservation in scientific applications. Equivariance, meaning the model’s output changes predictably under transformations (like rotations), is crucial for modeling physical systems. Standard diffusion models often lack this property, limiting their accuracy and interpretability when applied to scenarios with inherent symmetries (molecular structures, etc.). By incorporating equivariance into the diffusion process, the model ensures that its predictions respect the underlying symmetries, leading to more accurate and physically meaningful results. This is achieved through careful design of the diffusion process and the neural network architecture to ensure the model’s predictions transform consistently with the input transformations. The result is a generative framework capable of accurately modeling complex systems while preserving their fundamental symmetries, ultimately facilitating improved predictions and enhancing our understanding of scientific phenomena.

Trajectory Leverage

#

Leveraging trajectories in scientific modeling offers significant advantages over static approaches. By incorporating temporal dynamics, models can learn not just the initial and final states but also the intermediate steps of a process, thus capturing a more complete and nuanced representation. This is especially beneficial when dealing with complex systems where the transition between states isn’t straightforward, improving prediction accuracy and providing valuable insights into the underlying mechanisms. However, effectively using trajectory data requires careful consideration of computational cost and data availability. Equivariant techniques, which maintain symmetry despite transformations, are especially critical for ensuring the model’s robustness and interpretability when analyzing geometric states, which are frequently involved. Data efficiency is enhanced, allowing for the modeling of systems where fully-sampled trajectories might be scarce or expensive to obtain. This comprehensive approach bridges the gap between traditional methods and more modern deep learning techniques, yielding more accurate and scientifically valuable models.

GDB Framework

#

The Geometric Diffusion Bridge (GDB) framework presents a novel approach to predict geometric state evolution in complex systems. It leverages a probabilistic generative modeling approach, moving beyond limitations of traditional and deep learning methods. GDB’s core innovation is the use of an equivariant diffusion bridge, a modified Doob’s h-transform, to probabilistically connect initial and target geometric states. This addresses the challenge of modeling joint state distributions while respecting inherent symmetries. The framework seamlessly incorporates trajectory data, further enhancing accuracy by modeling dynamics through chains of equivariant diffusion bridges. Theoretical analysis proves GDB’s ability to preserve joint distributions and model underlying dynamics accurately. Empirical evaluations demonstrate superior performance across various real-world scenarios, making GDB a promising tool for scientific challenges in fields like quantum chemistry and material science.

Future Directions

#

The paper’s ‘Future Directions’ section would ideally explore several key avenues. Extending GDB to more complex geometric systems beyond molecules and catalysts is crucial. This could involve tackling larger-scale simulations, handling diverse interatomic interactions, or incorporating quantum effects. Investigating more sophisticated score estimation techniques is needed to further improve accuracy and efficiency. Developing more effective methods to incorporate trajectory data would enhance prediction accuracy, especially for scenarios with incomplete or noisy trajectories. Finally, a thorough exploration of the framework’s limitations and potential biases is important for responsible development. This includes analyzing the impact of different hyperparameters, and assessing the model’s robustness to noisy or incomplete data. Addressing these future directions would significantly enhance the applicability and reliability of the GDB framework.

More visual insights

#

More on figures

This algorithm describes the training process of the Geometric Diffusion Bridge model. It involves iteratively sampling initial and target geometric states from the data distribution, sampling intermediate states using a Brownian bridge-like process, and updating the model parameters via gradient descent to minimize the difference between the predicted score and the ground truth score.

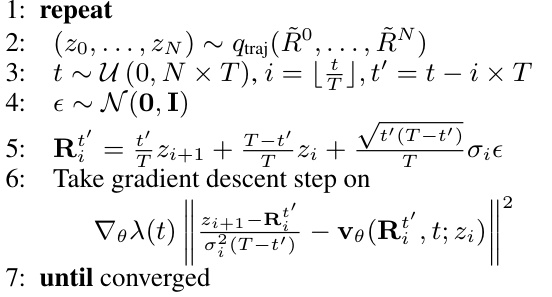
This algorithm details the training process of the Geometric Diffusion Bridge model when trajectory data is available. It leverages the chain of equivariant diffusion bridges, iteratively refining the model’s ability to predict future geometric states by incorporating information from intermediate states along the trajectory. The algorithm samples from the trajectory distribution, constructs bridges between consecutive states using a modified Doob’s h-transform, estimates the score function, and updates model parameters via gradient descent.

More on tables

This table compares various methods for bridging geometric states, focusing on their ability to satisfy symmetry constraints, preserve coupling between initial and target states, and leverage trajectory guidance. It highlights the advantages of the proposed Geometric Diffusion Bridge (GDB) method over existing approaches.

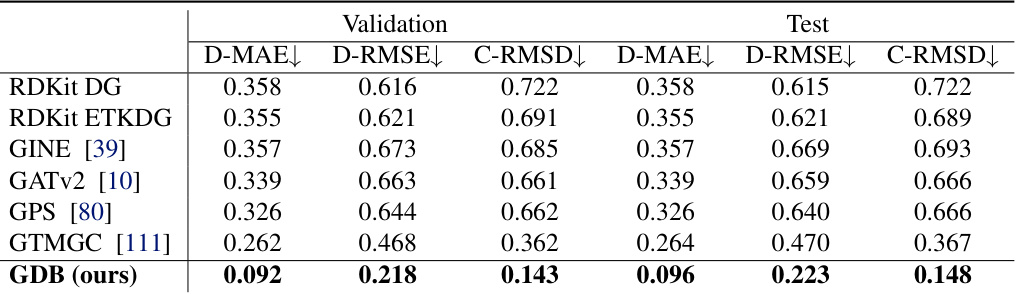
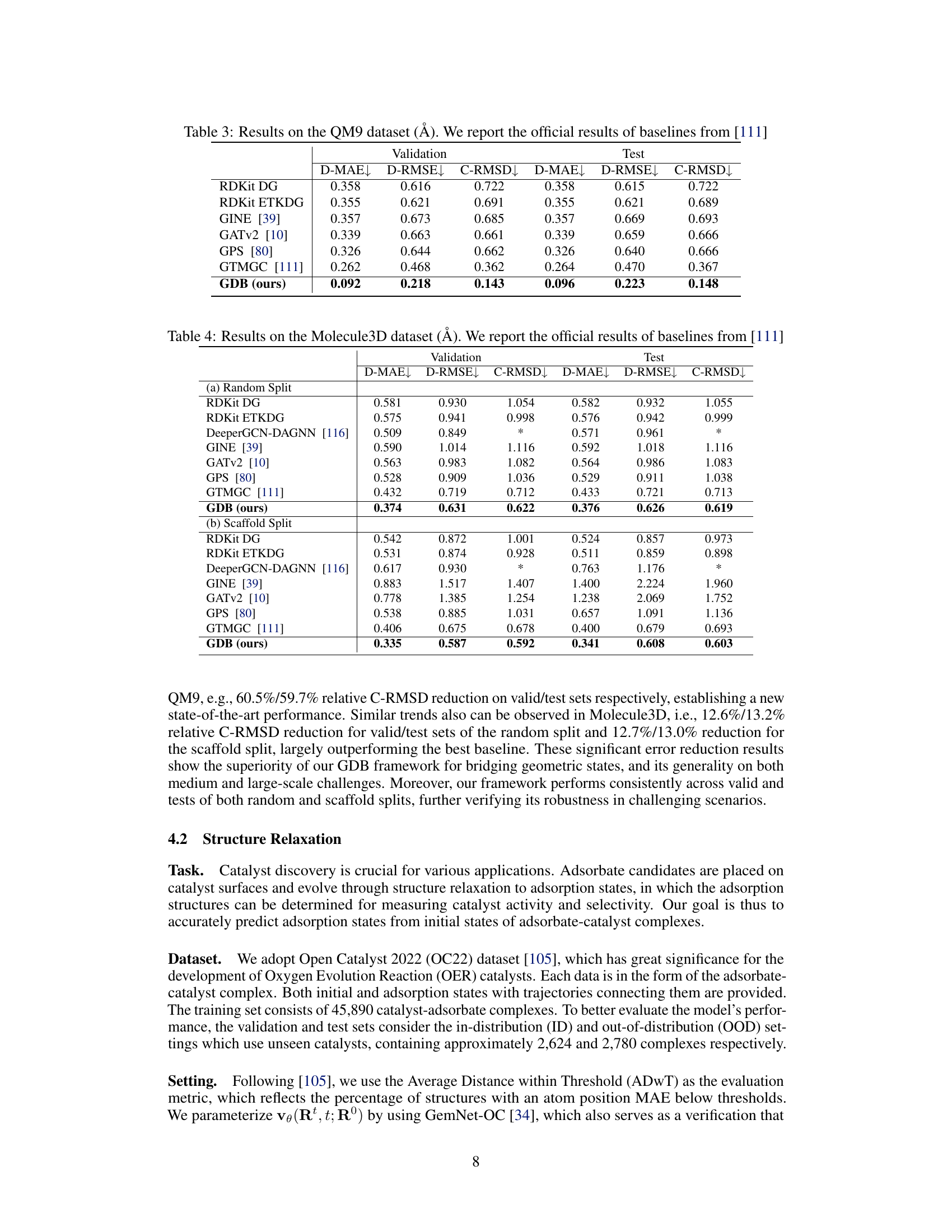
This table presents a comparison of the performance of various methods on the QM9 dataset for equilibrium state prediction. The results are measured in Angstroms (Å) and include three metrics: D-MAE (Mean Absolute Error of interatomic distances), D-RMSE (Root Mean Square Error of interatomic distances), and C-RMSD (Root Mean Square Deviation of Cartesian coordinates after rigid alignment). The table shows that the proposed Geometric Diffusion Bridge (GDB) method significantly outperforms other state-of-the-art methods on this benchmark.

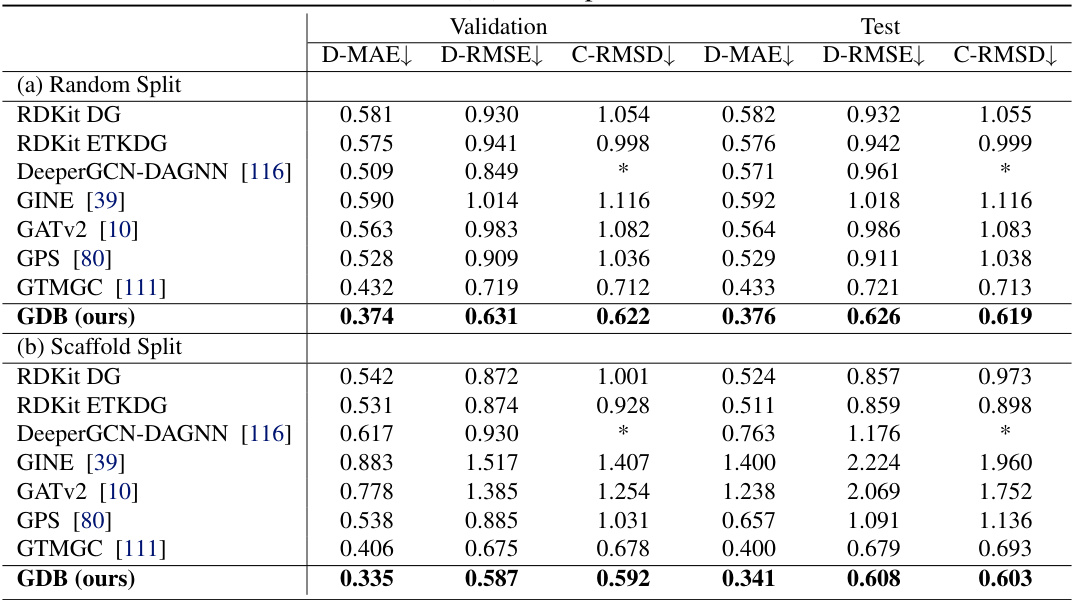
This table presents a comparison of the GDB model’s performance against several baselines on the Molecule3D dataset for equilibrium state prediction. The results are shown using three metrics: D-MAE, D-RMSE, and C-RMSD, for both random and scaffold data splits. The ‘*’ indicates missing results for a particular baseline and metric combination.

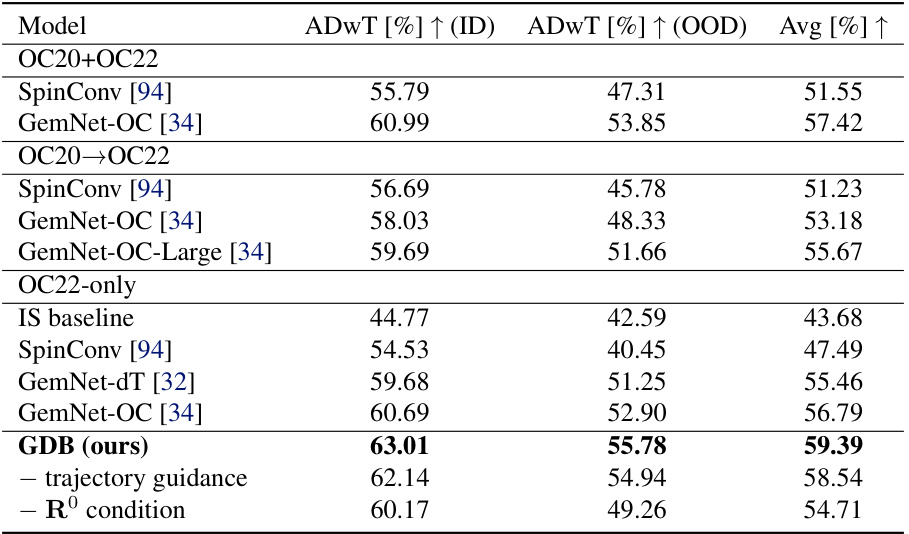
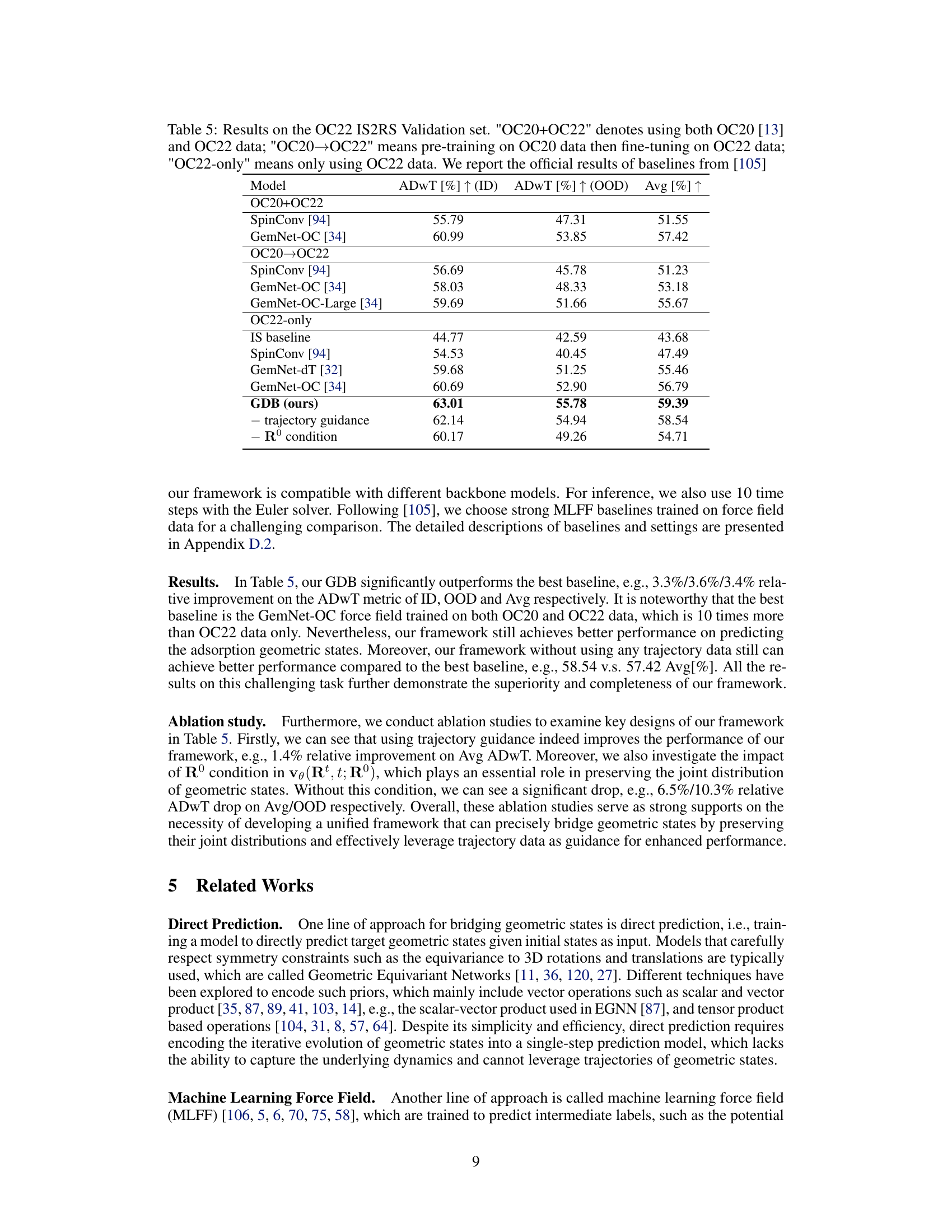
This table presents the results of the structure relaxation task on the OC22 IS2RS validation set. It compares the performance of the proposed Geometric Diffusion Bridge (GDB) method against several state-of-the-art baselines. The table shows the ADWT (Average Distance within Threshold) scores for in-distribution (ID) and out-of-distribution (OOD) data, as well as the average ADWT score across both. Different training setups for the baselines are also shown, indicating whether OC20 data was used in pre-training or fine-tuning. The results demonstrate the superior performance of GDB, especially when trajectory guidance is included.

Full paper

#