↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many explainable machine learning (XML) tasks, such as feature attribution and data valuation, involve computationally expensive calculations for each data point, posing challenges for large datasets. Current approximation methods, like Monte Carlo, often struggle with speed and accuracy, particularly for high-dimensional data. This significantly limits the scalability and applicability of these vital XML techniques.
This paper introduces a novel approach called “Stochastic Amortization” to overcome these limitations. The method cleverly leverages noisy, but unbiased, estimates of true labels to train an amortized model that directly predicts the desired outputs. Through theoretical analysis and extensive experiments, the authors demonstrate the effectiveness of their method across various XML tasks and datasets. The results show a substantial acceleration, often achieving an order-of-magnitude speedup compared to traditional methods, while maintaining high accuracy. The research provides a unified framework for training amortized models with noisy labels, broadening the applicability of these methods to more researchers and datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in explainable ML and related fields because it presents a novel and efficient method for addressing the computational limitations of existing attribution techniques. It opens up new avenues for research by showing how to leverage noisy labels effectively in training amortized models, thus accelerating many computationally intensive tasks with significant speedups. The work’s generalizability to various XML tasks and its theoretical justification make it widely relevant and impactful.
Visual Insights#

This figure compares two approaches for handling computationally expensive tasks in explainable machine learning (XML). The left side illustrates stochastic amortization, where noisy estimates of the true outputs are used to train an amortized model. This model then predicts the true outputs for new inputs. The right side shows the traditional per-instance computation method, where an expensive algorithm is run for each example, such as a Monte Carlo estimator.

This table summarizes various methods in explainable machine learning (XML) that utilize amortization, a technique to accelerate costly per-datapoint calculations. It categorizes these methods by problem type (e.g., Shapley value attribution, data valuation), context and output domains (representing input and output spaces), and computational approach (analytic, per-example optimization, regression-based amortization, or objective-based amortization). The table highlights the prevalence of amortization in addressing computationally expensive tasks within XML and reveals opportunities for new applications.
In-depth insights#
Stochastic Amortization#
Stochastic amortization presents a novel approach to accelerate computationally expensive explainable machine learning (XML) tasks by training amortized models with noisy labels. The core idea is to leverage inexpensive, unbiased estimates of true labels, like those from Monte Carlo approximations, to train a neural network that directly predicts the desired XML output (e.g., Shapley values for feature attribution). Theoretical analysis shows this approach is surprisingly effective even with high noise levels, provided that the noisy labels remain unbiased. The method’s efficiency stems from replacing per-instance calculations with a single, fast model prediction for the entire dataset. Experiments across various XML tasks and datasets demonstrate significant speedups, often an order of magnitude faster than per-example methods, showcasing the practical value of this unified approach. The approach’s robustness to noisy labels makes it applicable to a wide range of tasks where exact labels are difficult or expensive to obtain, significantly broadening the applicability of computationally expensive methods.
Noisy Label Training#
The concept of training machine learning models with noisy labels is a significant area of research, and it is particularly relevant to the paper’s approach of stochastic amortization. Noisy label training is a technique where the training data is imperfect, containing inaccuracies or errors in the labels. This contrasts with traditional supervised learning which assumes perfect, clean labels. The core challenge is to design methods robust enough to learn useful representations despite the label noise. The paper addresses this by focusing on unbiased noise, meaning the errors are random and not systematically skewed towards incorrect classifications. This characteristic allows the model to learn the correct underlying patterns, even with the presence of noise. Theoretical analysis in the paper helps to justify the effectiveness of training with noisy labels, providing a formal understanding of the impact of noise levels and bias on model accuracy and convergence. The work demonstrates that the proposed training methods are surprisingly effective, even with high noise levels, offering a substantial advantage over existing methods that require much more computationally expensive precise labels. Ultimately, noisy label training is crucial for making expensive explainable ML methods more practical and scalable, especially when dealing with large datasets where obtaining perfect labels is infeasible.
Explainable ML Speedup#
This research paper explores methods to significantly accelerate explainable machine learning (XML) techniques. A core contribution is stochastic amortization, a method that trains amortized models using noisy, yet unbiased, estimates of true labels. This is particularly valuable because obtaining exact labels for many XML tasks (like feature attribution and data valuation) is computationally expensive. The authors demonstrate that this approach is surprisingly effective, yielding substantial speedups compared to traditional per-example calculations. Theoretical analysis confirms the efficacy of stochastic amortization with noisy labels, showing that unbiasedness is key; label noise variance impacts convergence speed but does not fundamentally compromise accuracy. The paper covers multiple XML tasks, showcasing the broad applicability of the method, and extensive experiments validate the theoretical findings, showing order-of-magnitude speed improvements and robustness to high levels of label noise. The overall impact is a practical and efficient method to make many computationally intensive XML tasks feasible and scalable for large datasets.
XML Applications#
The section on “XML Applications” would delve into the practical uses of stochastic amortization within explainable machine learning (XML). It would likely showcase its efficacy across various XML tasks, demonstrating the method’s versatility and potential impact. Feature attribution, a core application, would be examined, possibly highlighting the acceleration of Shapley value calculations through noisy label training. Data valuation, another key area, would illustrate how stochastic amortization can quickly estimate the contribution of data points to a model’s accuracy. The discussion would likely include examples of models (e.g., fully-connected networks, convolutional neural networks, or transformers) and datasets, emphasizing the method’s performance across various data types and scales. Finally, the discussion would likely cover alternative feature attribution methods (like LIME or Banzhaf values), and how the principle of stochastic amortization could be extended and adapted for wider use in explainability. Generalizability and scalability would also be key themes, showing how stochastic amortization can significantly reduce computational costs and improve efficiency in several XML tasks, even when exact label information is not readily available.
Future Work#
The authors suggest several promising avenues for future research. Scaling to datasets with millions of examples is crucial to fully assess the limits of stochastic amortization with noisy labels, especially concerning the trade-off between using more noisy or fewer, higher-quality labels. Improving the efficiency and accuracy of stochastic amortization remains a goal, requiring exploration of more advanced unbiased estimators or more sophisticated model retraining methods. The broader applicability of stochastic amortization to other explainable machine learning (XML) tasks, such as evaluating the impact of model retraining, should be explored. Finally, investigating the use of noisy labels in diverse model interpretation techniques (e.g., datamodels), combined with a thorough analysis of bias and variance, offers significant potential.
More visual insights#
More on figures

This figure shows a comparison of Shapley value feature attributions obtained using three different methods: stochastic amortization, noisy labels (using KernelSHAP with 512 samples), and ground truth (using KernelSHAP with 1M samples). The figure visually demonstrates that the attributions predicted by the amortized model are much closer to the ground truth than the noisy labels, highlighting the effectiveness of the stochastic amortization approach in improving the accuracy of Shapley value estimations.
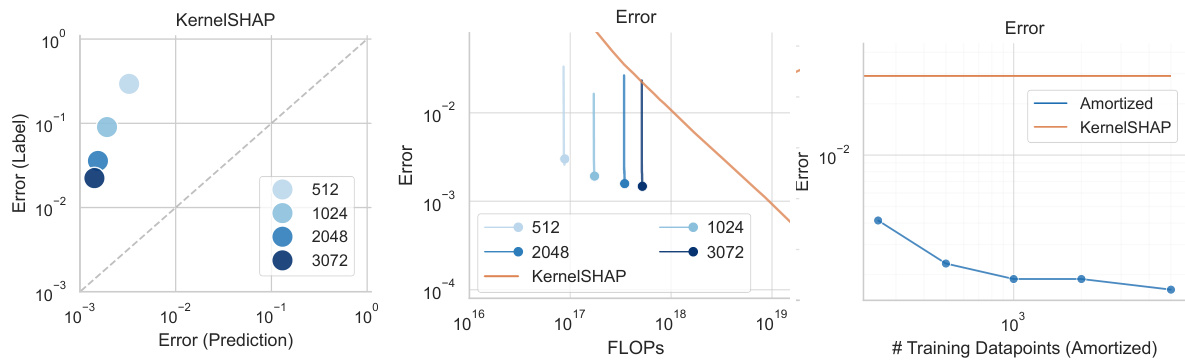
This figure compares the performance of amortized Shapley value feature attribution using KernelSHAP as a noisy oracle against per-instance KernelSHAP. The left panel shows the squared error decreases as the number of samples used for generating noisy labels increases. The center panel shows a comparison in estimation error as a function of FLOPs, demonstrating the efficiency of amortization. The right panel shows a compute-matched comparison using different dataset sizes, indicating the scalability and effectiveness of the method.

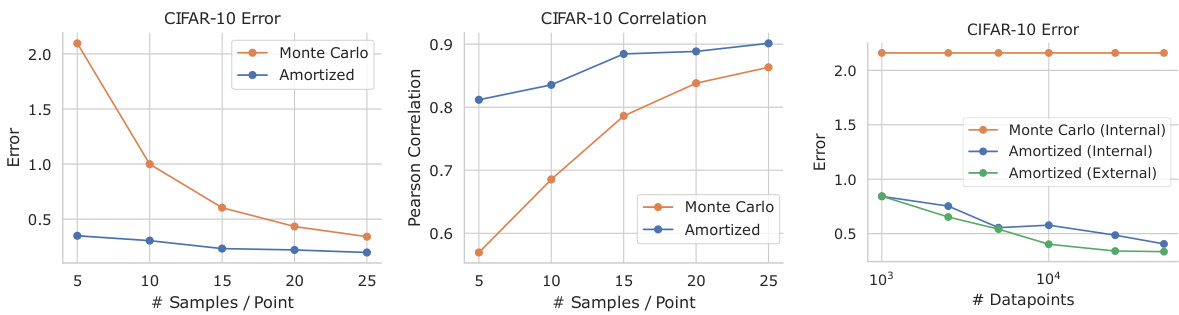
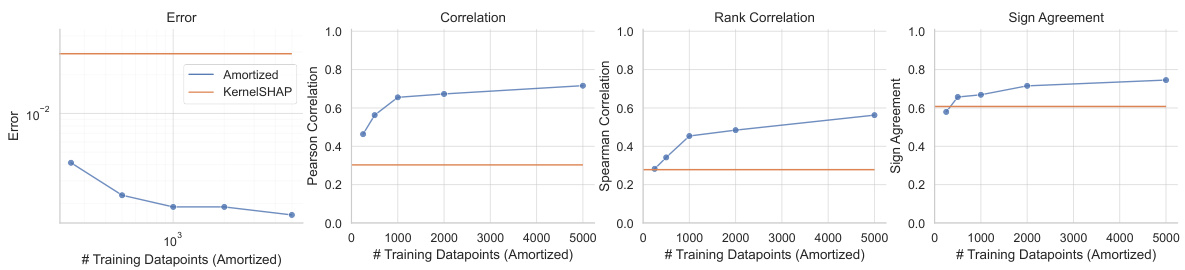
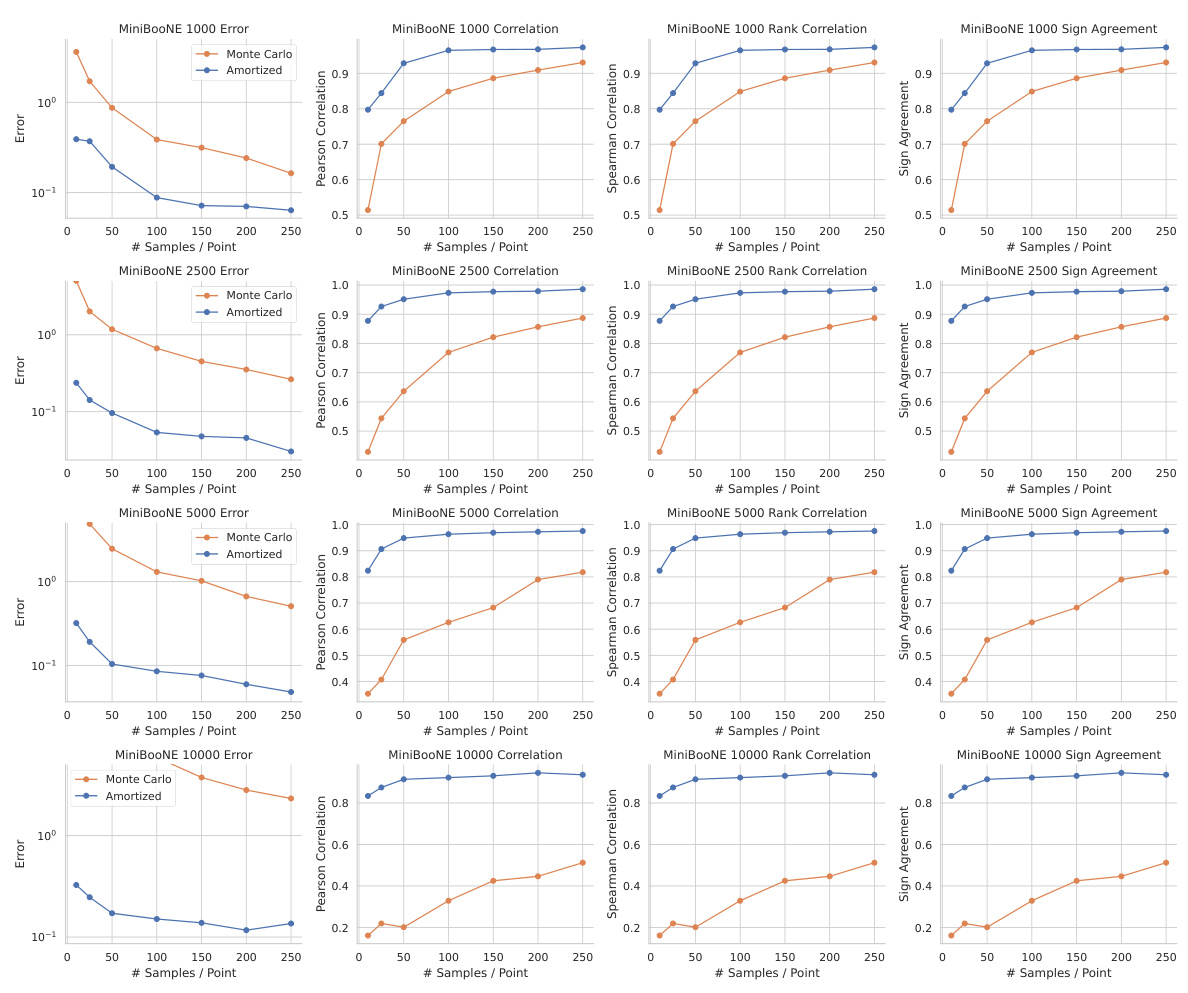
This figure compares the performance of amortized data valuation against the traditional Monte Carlo method for tabular datasets (MiniBooNE and Adult Census). The left and center panels focus on the MiniBooNE dataset, showing mean squared error and Pearson correlation with the ground truth for varying numbers of Monte Carlo samples used for the noisy oracle. The right panel demonstrates how the accuracy of both methods scales with increasing dataset size, maintaining a consistent use of 50 Monte Carlo samples per datapoint. The results show that amortization consistently outperforms the Monte Carlo approach in terms of accuracy and correlation with the ground truth, particularly as the dataset size increases.
This figure compares the performance of the proposed stochastic amortization method with the traditional KernelSHAP approach for Shapley value feature attributions. It shows three aspects: the effect of noisy label quality on error, the computational cost trade-off (FLOPs) between the methods, and how the accuracy changes with training dataset size while maintaining equal per-datapoint computation budget.

This figure compares the results of using stochastic amortization for Shapley value feature attributions against two baselines: noisy labels (generated using KernelSHAP with 512 samples) and ground truth (generated using KernelSHAP with 1M samples). The results demonstrate that stochastic amortization is able to significantly improve the accuracy of noisy label estimates, approaching the accuracy of ground truth while using substantially fewer samples.

This figure compares the performance of amortized Shapley value feature attribution with different noise levels, computational costs, and training dataset sizes. The left panel shows that the error decreases as the number of samples used to generate the noisy labels increases. The center panel shows that amortized model achieves lower error with significantly lower FLOPs compared to KernelSHAP. The right panel shows the error comparison for varying training set sizes when the computational budget is fixed.
This figure compares the performance of the proposed stochastic amortization method with the traditional KernelSHAP method for Shapley value feature attribution. The left panel shows the error decreases as the number of samples used for KernelSHAP increases (noise level decreases). The center panel compares the estimation error as a function of FLOPs (floating-point operations), demonstrating the computational efficiency of amortization. The right panel shows the error with varying training dataset sizes, illustrating that amortization is more efficient even with smaller datasets, when computation is matched between the two approaches.

This figure compares the performance of amortized Shapley value feature attribution with the standard KernelSHAP approach. The left panel shows that the amortized model achieves lower error than the noisy oracle labels, even with a small number of samples. The center panel shows that, in terms of FLOPs, the amortized model is much more efficient and that the error further decreases with increased training. The right panel further demonstrates that the amortized model consistently outperforms the KernelSHAP approach, given a fixed computational budget per data point.
The figure displays the results of using stochastic amortization for Shapley value feature attribution. It shows the error rates compared to ground truth attributions, considering varying noise levels in the training data and computational cost (FLOPs). The three sub-figures show how the error varies with sample size, FLOPs, and dataset size.
The figure shows the results of applying stochastic amortization to Shapley value feature attribution using KernelSHAP as the noisy oracle. The left panel shows the error decreases as more samples are used in the KernelSHAP approximation. The center panel compares the error against FLOPs (floating-point operations), demonstrating amortization is significantly faster. The right panel compares the error for different dataset sizes given the same compute budget, showcasing amortization’s efficiency, particularly in larger datasets.
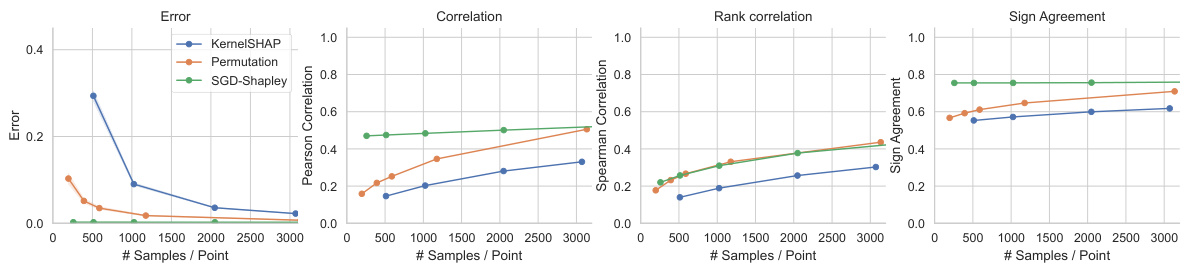
This figure compares the performance of the proposed stochastic amortization method against the standard KernelSHAP method for Shapley value feature attribution. The left panel shows that amortization significantly reduces the error compared to using noisy labels, especially when the number of samples used for generating the noisy labels is small. The center panel demonstrates that amortization requires less computation (measured in FLOPs) to achieve a similar level of accuracy. The right panel shows that, when the compute budget is matched between the two methods, amortization achieves better accuracy, especially for larger datasets.
This figure compares the performance of stochastic amortization against the standard per-example KernelSHAP method for Shapley value feature attribution. It shows three plots demonstrating the effect of (left) noise level on estimation error, (center) computational cost (FLOPs) on estimation error, and (right) the size of training data on estimation error while maintaining a similar computational budget. The results indicate that stochastic amortization consistently outperforms the per-example method across all three scenarios.
This figure demonstrates the effectiveness of stochastic amortization for Shapley value feature attribution. The left panel shows the error decreases as the number of samples used to generate noisy labels increases. The center panel compares the computational cost (FLOPs) of KernelSHAP and the amortized model, demonstrating that amortization is more efficient. The right panel shows that amortization achieves lower estimation error for datasets of various sizes when computation is matched across methods.
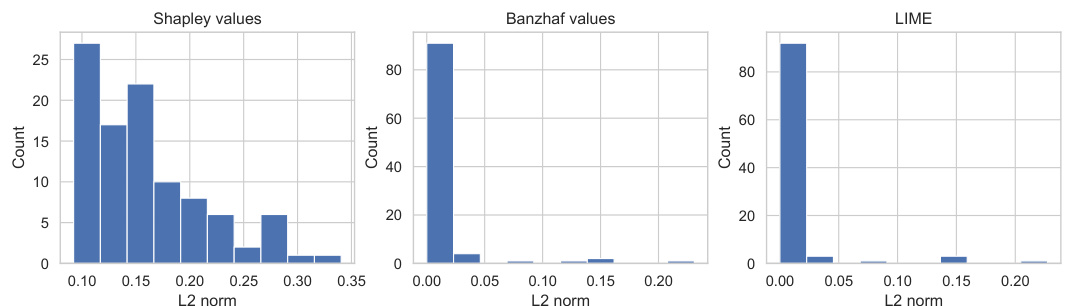
This figure shows the distribution of L2 norms for Shapley values, Banzhaf values, and LIME attributions. The x-axis represents the L2 norm, and the y-axis represents the count. The distributions are shown in histograms. The figure illustrates that Shapley values tend to have larger norms compared to Banzhaf values and LIME attributions, which have norms concentrated at small magnitudes with a long tail of larger values. This difference in scale affects the performance of the amortization for each method, as discussed in the paper.

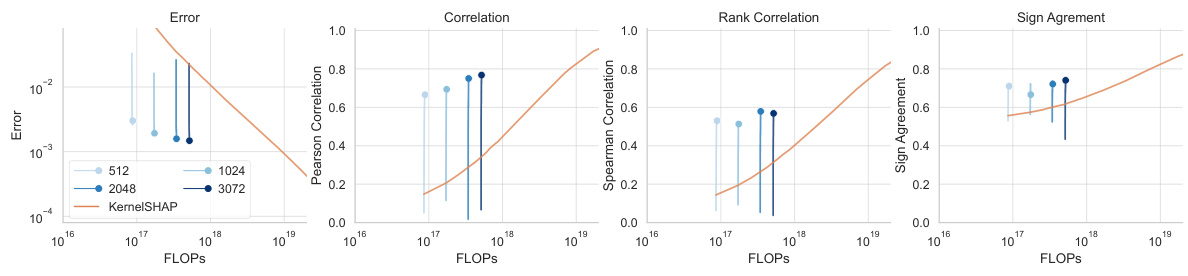
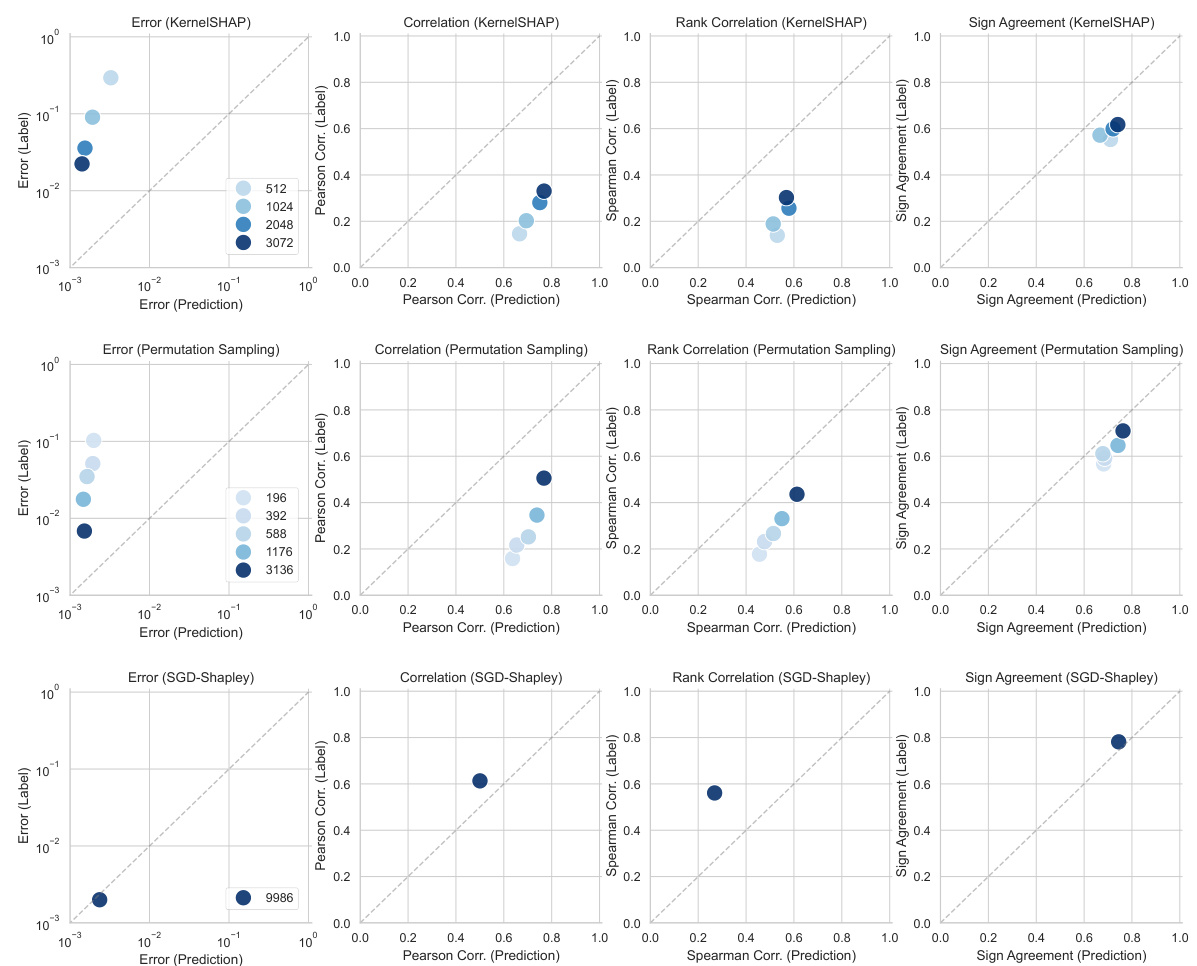
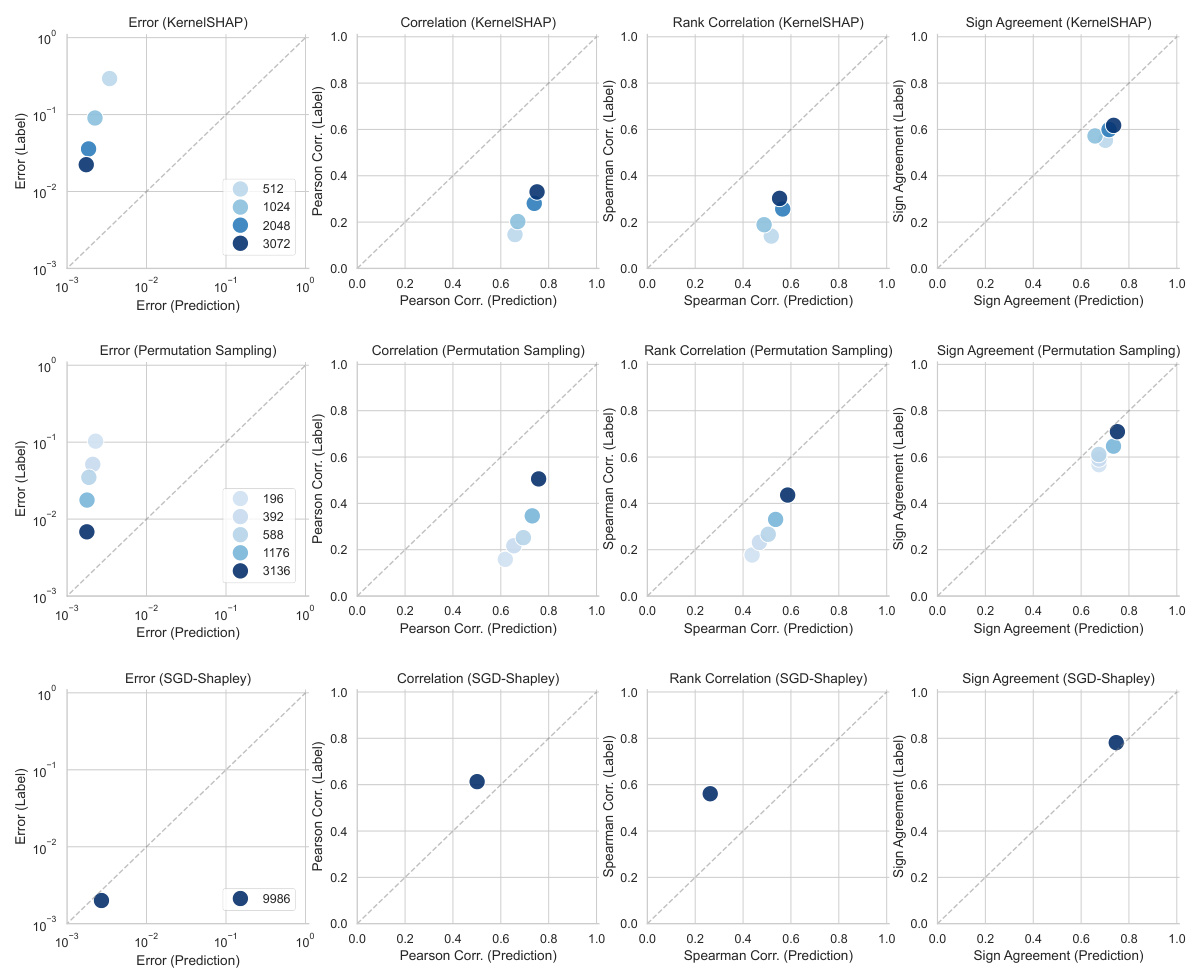
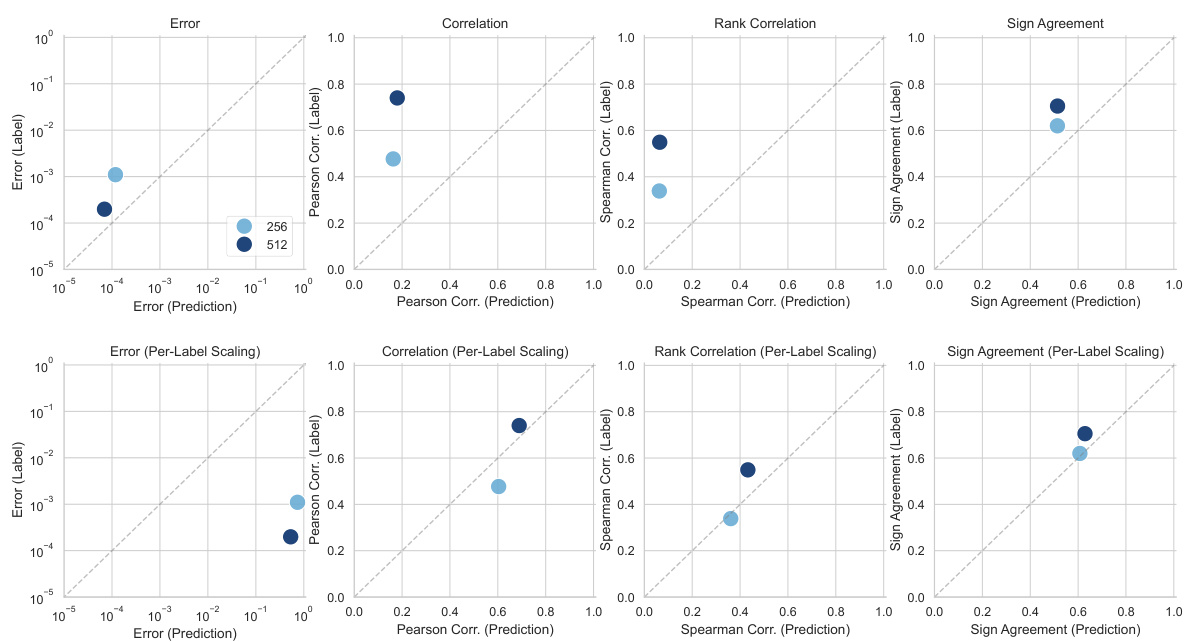
This figure compares the estimation errors of three different methods for generating noisy labels (KernelSHAP, permutation sampling, and SGD-Shapley) with amortized predictions for Shapley value feature attributions. It shows the performance of these methods with different numbers of samples used to generate the labels. The comparison is done using various metrics like error, correlation (Pearson and Spearman), and sign agreement.
This figure compares the performance of amortized Shapley value feature attribution against KernelSHAP with respect to different noise levels, FLOPs, and training data sizes. The left panel shows the impact of the number of KernelSHAP samples (noise level) on the error. The center panel compares the error as a function of FLOPs (floating-point operations) showing the trade-off between the computation cost of obtaining noisy labels and the cost of training the amortized model. The right panel demonstrates error as a function of training set size, keeping a fixed compute budget for both methods.
The figure displays a comparison of the performance of stochastic amortization against the KernelSHAP method for Shapley value feature attribution. Three subplots illustrate the results: (Left) estimation error based on noisy labels with varied sample sizes; (Center) a comparison of FLOPs required for the methods to estimate the attributions; and (Right) estimation error against varying training dataset sizes with matched computational budgets. The results demonstrate that amortization yields significant improvements.

This figure shows the results of the Shapley value feature attribution experiments using KernelSHAP as a noisy oracle. The left panel shows the squared error of the attributions decreases as the number of KernelSHAP samples increases (reducing noise). The center panel demonstrates that amortized predictions achieve lower error for the same computational cost (FLOPs), as training the amortized model is cheap relative to repeated exact computation. The right panel highlights that the error decreases as the training set size grows, while maintaining equivalent compute per data point by using fewer KernelSHAP samples for noisy labels.

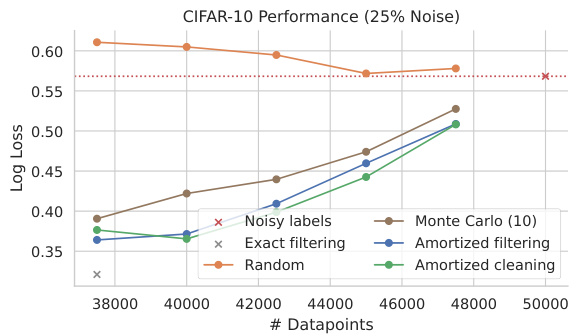
This figure compares the performance of Monte Carlo and amortized methods for estimating distributional data valuation scores on the CIFAR-10 dataset. Four metrics are used to evaluate the accuracy of the estimations: squared error, Pearson correlation, Spearman correlation, and sign agreement. The results show how the accuracy of both methods improves as the number of samples per data point increases, but the amortized method consistently outperforms the Monte Carlo method.

This figure shows the results of distributional data valuation experiments on CIFAR-10 dataset using 50K data points. It compares the performance of Monte Carlo estimates and amortized estimates against ground truth values, using different numbers of samples per data point. Four evaluation metrics are employed: squared error, Pearson correlation, Spearman correlation, and sign agreement. The results illustrate the accuracy and efficiency of the amortized approach in data valuation.
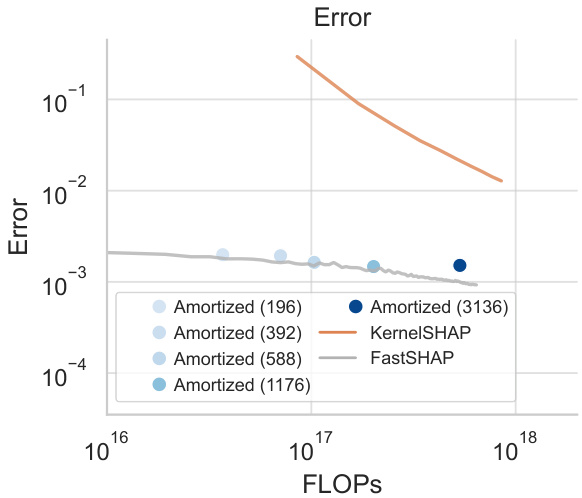
This figure compares the performance of stochastic amortization with FastSHAP and KernelSHAP for Shapley value feature attributions. The x-axis represents total FLOPs, while the y-axis represents the error in the estimated Shapley values. It demonstrates that stochastic amortization achieves comparable accuracy to FastSHAP, while both methods significantly outperform KernelSHAP, especially when using more computationally expensive methods. The results suggest that stochastic amortization is a computationally efficient and accurate alternative for calculating Shapley values.
Full paper#



















