↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many AI-driven design problems leverage generative modeling for exploring design spaces and model-based optimization for refining designs using reward functions. However, existing methods often struggle in offline scenarios where accurate reward models are unavailable, leading to over-optimization. This paper introduces BRAID, a novel approach that tackles these challenges by conservatively fine-tuning diffusion models using a learned reward model that incorporates uncertainty quantification and penalizes out-of-distribution regions. This helps prevent overfitting to the limited training data and avoid generating invalid designs.
BRAID achieves this by optimizing a conservative reward model that incorporates uncertainty quantification terms. It then uses this reward model to fine-tune a pre-trained diffusion model, adding a KL-divergence penalty to ensure that generated designs remain within the valid design space. This “doubly conservative” approach ensures high-quality designs that outperform the best designs in the offline dataset. The paper demonstrates BRAID’s efficacy through empirical evaluations in diverse domains, including DNA/RNA sequences and images, showcasing its significant improvement over existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI-driven design and generative modeling because it presents a novel approach, BRAID, that effectively bridges model-based optimization and generative modeling. BRAID addresses the limitations of existing methods in offline settings, where accurate reward models are unavailable, opening doors for more efficient and robust design optimization in various scientific domains. Its theoretical framework and empirical results demonstrate significant potential for improving various design problems and offer a valuable contribution to current research trends.
Visual Insights#

The figure illustrates the setup of the proposed algorithm. The left panel shows the pre-trained diffusion model and offline data used as input. The right panel visualizes the algorithm’s goal: to improve designs by fine-tuning a pre-trained generative model using a reward model learned from offline data. The figure highlights the valid design space within the larger design space and emphasizes the challenge of over-optimization in regions with sparse data. It shows how the algorithm adds penalties in data-sparse regions to prevent overfitting and uses a KL penalty to keep generated designs within the valid space.
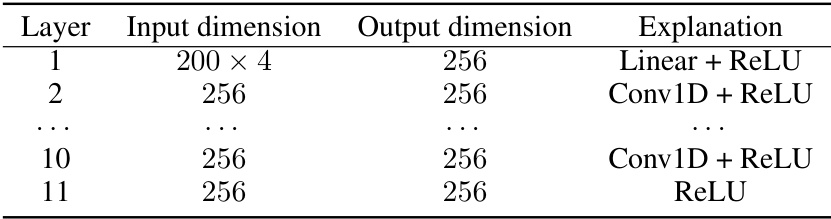
This table shows the architecture of the neural networks used for diffusion models in the paper. It details the input and output dimensions for each layer, along with the activation functions used. This architecture is specifically designed for modeling biological sequences.
In-depth insights#
Offline RL for Design#
Offline reinforcement learning (RL) presents a unique opportunity for design optimization problems. Traditional RL methods rely on extensive online interactions, often impractical in many design settings due to the high cost or time constraints associated with obtaining feedback. Offline RL, using pre-collected datasets, offers a promising alternative. In design, this translates to leveraging historical design data (simulations, experiments) to train an RL agent that can generate improved designs without needing new simulations or experiments for each iteration. However, challenges arise in handling biases and limitations inherent in offline datasets. These datasets might not comprehensively represent the entire design space or contain noisy/sparse reward signals, potentially misleading the learned policy. To tackle these issues, conservative offline RL techniques that place more emphasis on regions of known reliability, incorporate uncertainty estimations, and reduce extrapolation errors are crucial. The use of generative models in conjunction with offline RL is also valuable, generating candidate designs that can then be evaluated and further refined by the RL agent. Such hybrid approaches offer a powerful framework for efficiently exploring a vast design space while mitigating risks associated with limited or unreliable offline data.
BRAID: A New Approach#
BRAID presents a novel approach to AI-driven design problems by bridging the gap between generative modeling and model-based optimization. Unlike previous methods which often assume readily available reward models, BRAID tackles the more realistic scenario of an offline setting with limited, static data. The approach cleverly uses conservative fine-tuning of pre-trained diffusion models, preventing over-optimization by penalizing designs outside the observed data distribution. This ensures that generated designs remain valid and high-quality, leveraging the power of reward models for extrapolation without risking the generation of unrealistic or invalid outputs. BRAID’s doubly conservative strategy, incorporating both reward and KL penalties, is theoretically grounded, providing a regret guarantee and empirically showing superior performance across diverse tasks like DNA/RNA sequence and image generation.
Conservative Tuning#
Conservative tuning, in the context of AI model training, particularly diffusion models, emphasizes mitigating the risks associated with over-optimization. Standard fine-tuning methods might exploit uncertainties in reward models, leading to poor generalization. Conservative approaches, as explored in the paper, address this by incorporating penalty terms that discourage the model from venturing into data regions where the reward model’s confidence is low or where the model might generate invalid designs. This strategy promotes generalization and avoids adversarial designs by encouraging the model to remain within the well-understood regions of the data distribution. The effectiveness of conservative tuning depends crucially on the design of the penalty function, which needs to carefully balance exploration and exploitation. The paper’s proposal of a doubly conservative approach that combines both reward model conservatism and KL regularization on the diffusion process is particularly interesting, as it suggests a more robust strategy that directly addresses concerns about model overfitting and out-of-distribution generalization.
Extrapolation Limits#
The concept of ‘Extrapolation Limits’ in the context of AI-driven design is crucial. It highlights the inherent risk of relying solely on learned reward models, especially in offline settings, where the model’s understanding of the design space is limited to the provided data. When an AI attempts to optimize beyond the bounds of this data (extrapolation), it may encounter regions of the design space where the reward model is inaccurate or undefined. This could lead to over-optimization and the generation of designs that are not only suboptimal but also invalid. The success of an AI-driven design process hinges on carefully considering and mitigating these limits. Conservative approaches that incorporate uncertainty quantification or penalization mechanisms outside the training data distribution are therefore vital for reliable extrapolation and to ensure that designs remain feasible within the true design space. Theoretical guarantees that bound the performance degradation due to extrapolation are highly desirable and necessary to ensure the trustworthiness of AI-driven design optimization.
Future Work: Open Set#
The concept of “Future Work: Open Set” in the context of AI-driven design problems suggests a significant direction for future research. The current methods often rely on closed-set assumptions, meaning that the model is trained only on data representing the known design space. This limitation restricts the model’s ability to generate novel or unexpected designs, hindering creativity and potentially missing optimal solutions. Extending AI-driven design to the open-set setting, where the model encounters unseen designs and learns to classify and extrapolate appropriately, will be crucial. This requires developing robust techniques that handle uncertainty, outlier detection, and generalization to novel design features effectively. A key challenge lies in creating learning methods that allow the model to distinguish between truly novel designs and simply invalid designs. Robustness is crucial as the model must avoid being misled by outliers or invalid designs during open-set testing, maintaining its ability to extrapolate appropriately. A promising avenue is combining generative models with mechanisms for uncertainty quantification, allowing for cautious exploration of uncharted design spaces. Further research should explore how to incorporate human feedback effectively in an open-set setting to steer the model towards desired solutions, improving the model’s ability to generalize and create truly innovative designs.
More visual insights#
More on figures
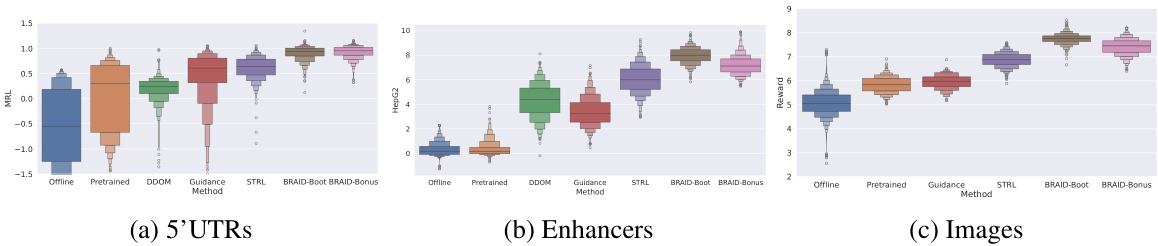
This figure displays box plots comparing the rewards achieved by different methods for generating samples (5’UTRs, enhancers, and images). Each box plot represents a method: Offline (the original data), Pretrained (the initial diffusion model), DDOM, Guidance, STRL, BRAID-Boot, and BRAID-Bonus. The y-axis represents the reward value (r(x)). The figure visually demonstrates that the BRAID methods consistently yield higher rewards than other approaches, suggesting the effectiveness of the conservative fine-tuning technique.
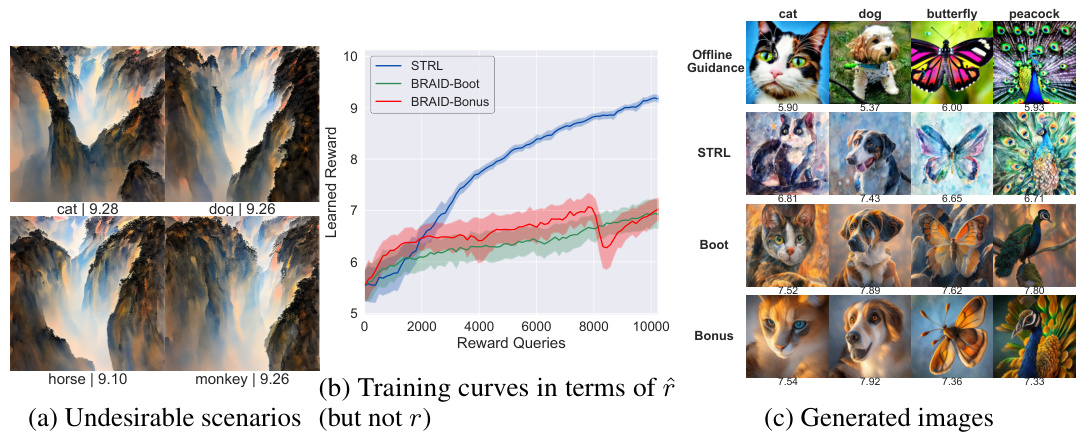
This figure compares the performance of different algorithms for generating samples, measured by the reward function r(x). The bar plots show the distribution of rewards obtained for samples generated by each algorithm. The key observation is that the algorithms introduced in the paper consistently yield higher rewards than the baseline algorithms, indicating superior performance in generating high-quality samples.

This figure displays bar plots comparing the rewards (r(x)) obtained from samples generated by different methods: Offline, Pretrained, DDOM, Guidance, STRL, BRAID-Boot, and BRAID-Bonus. The x-axis represents the methods, and the y-axis represents the reward values. The height of each bar indicates the average reward achieved by that method. The plot visually demonstrates that the BRAID methods consistently achieve higher average rewards compared to the baseline methods. This suggests that the proposed conservative fine-tuning approaches outperform other methods in generating high-quality designs.

This figure displays bar plots illustrating the reward scores (r(x)) obtained from samples generated using various methods. The algorithms compared include Offline (using only data from the offline dataset), Pretrained (using a pre-trained generative model), DDOM (a conditional diffusion model), Guidance (an offline guidance method), STRL (a standard reinforcement learning based fine-tuning approach), BRAID-Boot (the proposed method using bootstrapping to estimate uncertainty), and BRAID-Bonus (the proposed method using a bonus term for uncertainty). The plots show that the BRAID methods consistently achieve higher reward scores than the baseline methods, demonstrating their effectiveness in generating high-quality designs.

This figure presents bar plots comparing the reward scores (r(x)) obtained from samples generated using different methods: Offline, Pretrained, DDOM, Guidance, STRL, BRAID-Boot, and BRAID-Bonus. The rewards represent the quality of the generated designs. The bar plots visually demonstrate the relative performance of each method, showing that the BRAID methods (BRAID-Boot and BRAID-Bonus) consistently achieve higher reward scores than the other methods, indicating their superior performance in generating high-quality designs. The Offline and Pretrained methods represent the baseline performance before any optimization.
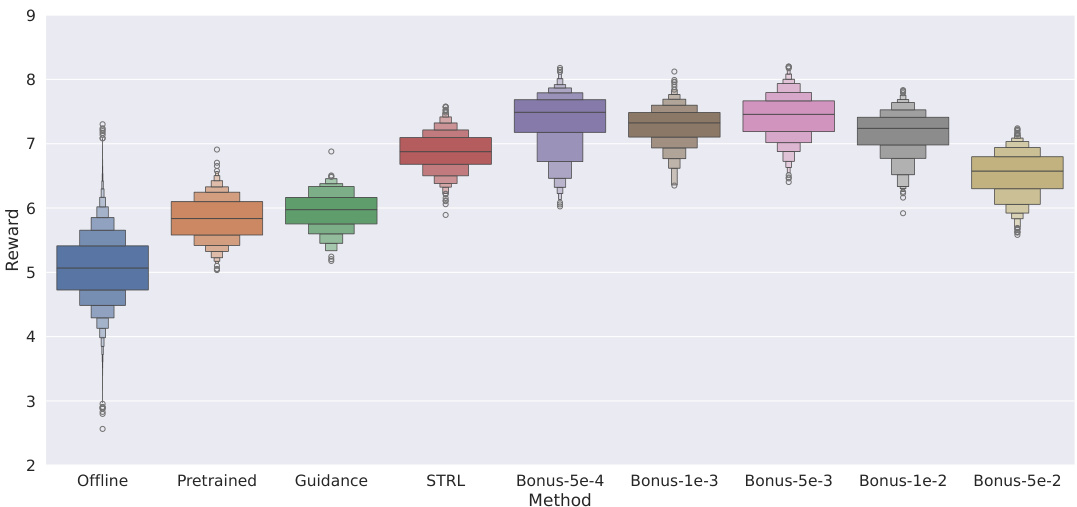
This figure displays the results of several reward-based generative modeling methods in terms of the average reward obtained. The bar plots show that the rewards from the samples generated by the proposed BRAID method (with both bonus and bootstrap approaches) consistently surpass the rewards achieved by the baseline methods, such as STRL, DDOM, and Guidance. This indicates that the proposed BRAID method is superior in generating samples with better reward values than other methods. The figure includes error bars representing the uncertainty in the reward values.

This figure compares the performance of different methods for generating samples (designs). Each method is used to generate samples, and the reward (r(x)) for each sample is calculated. The bar plots show the distribution of rewards for samples generated by each method. The results indicate that the proposed methods (BRAID-Boot and BRAID-Bonus) consistently achieve higher rewards compared to the baseline methods (Offline, Pretrained, DDOM, Guidance, STRL).
More on tables

This table lists the hyperparameters used in the fine-tuning process for all methods mentioned in the paper. It includes parameters such as batch size, KL parameter alpha, LCB parameter (bonus) c, the number of bootstrap heads, the sampling method used (Euler Maruyama), the step size used during fine-tuning, and the guidance level and target. These parameters are crucial to the performance and reproducibility of the experiments.

This table details the architecture of the neural networks used for the diffusion models in the paper. It shows the input and output dimensions for each layer, along with the activation function used. The architecture is designed for processing biological sequences, and is a key component in the proposed BRAID method for generating high-quality designs.

This table lists the hyperparameters used for fine-tuning the diffusion models. It includes parameters for BRAID (including the bonus parameter c), STRL, and offline guidance. The optimization parameters (optimizer, learning rate, weight decay, gradient clipping, and truncated backpropagation steps) are also listed and are consistent across all methods.

This table presents the results of evaluating the generated images using LLaVA, a large multi-modal model. It shows the mean, minimum, and maximum LLaVA scores for 400 generated samples, comparing the pre-trained model and several checkpoints of the STRL algorithm. The crucial aspect is the ‘invalid/total samples’ column, which indicates the number of images deemed invalid (i.e., not correctly aligned with the prompt) out of the total 400 samples. This metric helps to quantify the level of over-optimization, which is a significant issue addressed in the paper.
Full paper#



















