Entrywise error bounds for low-rank approximations of kernel matrices

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on low-rank approximations of kernel matrices, especially in machine learning. It provides novel entrywise error bounds, which are important for applications where individual errors matter significantly (e.g., healthcare, system control). The paper’s delocalisation results for kernel matrix eigenvectors and new concentration inequality are important theoretical contributions that will likely influence future research in random matrix theory and kernel methods.

Visual Insights

#

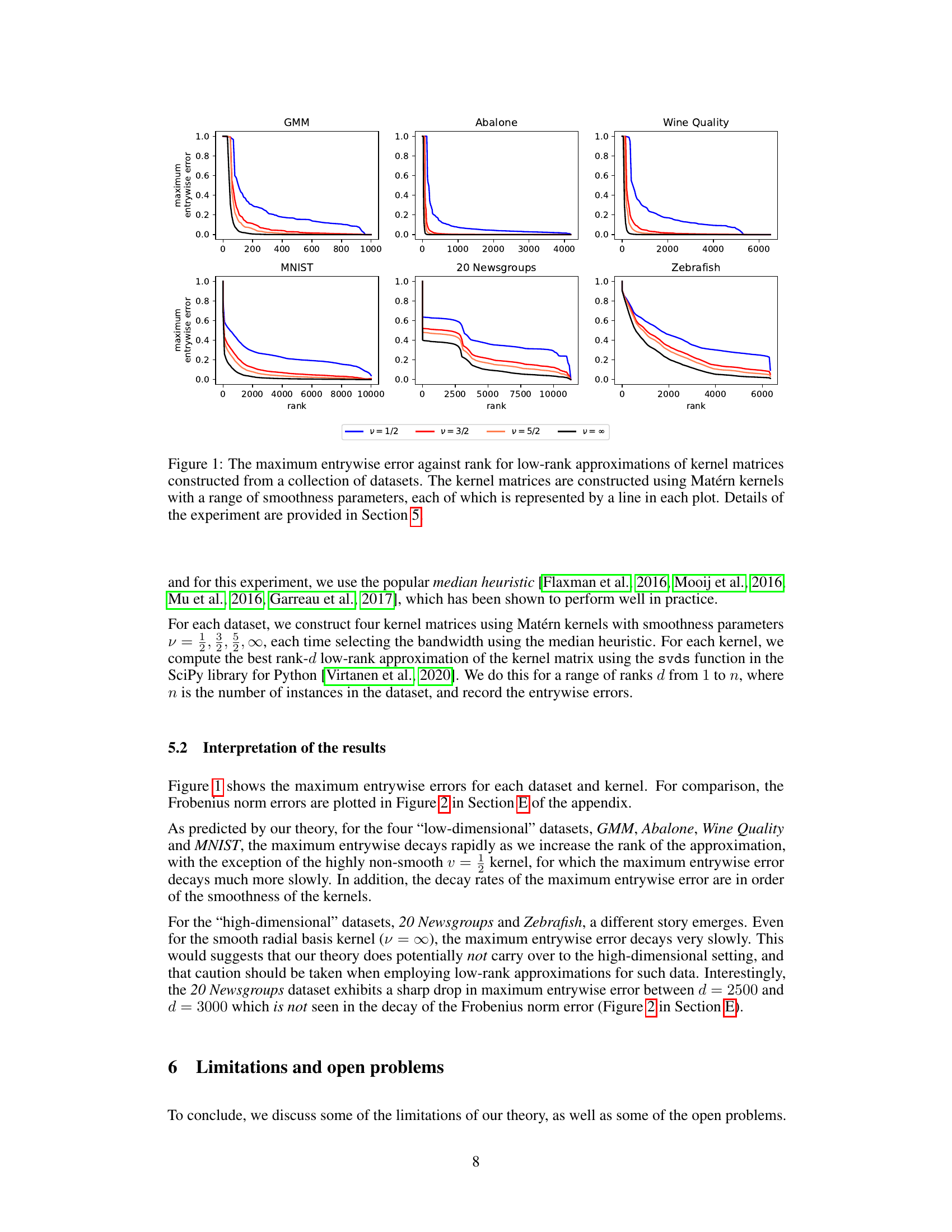
The figure shows the maximum entrywise error for low-rank approximations of kernel matrices for six datasets (GMM, Abalone, Wine Quality, MNIST, 20 Newsgroups, Zebrafish). Each dataset uses Matérn kernels with varying smoothness parameters (v = 1/2, 3/2, 5/2, ∞). The x-axis represents the rank of the approximation, and the y-axis represents the maximum entrywise error. The plots illustrate how the maximum entrywise error decreases as the rank increases, with smoother kernels exhibiting faster decay rates. The high-dimensional datasets (20 Newsgroups and Zebrafish) show slower decay compared to the low-dimensional datasets.

This table summarizes the three main hypotheses used in the paper’s main theorem: (P) describes polynomial eigenvalue decay; (E) describes exponential eigenvalue decay; and (R) describes regularity conditions involving eigenfunctions. The table specifies the mathematical expressions and requirements for each hypothesis, which concern the decay rate of eigenvalues and the supremum norm of eigenfunctions, and how these relate to certain quantities Δᵢ and Γᵢ that are defined in the paper. These hypotheses are key to understanding the entrywise error bounds for low-rank approximations of kernel matrices.

In-depth insights

#

Entrywise Error Bounds

#

Entrywise error bounds offer a crucial refinement to traditional error metrics in low-rank matrix approximations. Instead of focusing solely on global measures like the Frobenius or spectral norms, entrywise bounds analyze the error of individual matrix entries. This granular perspective is particularly valuable in applications where individual errors have significant costs, such as healthcare or system control. The paper’s focus on entrywise error reveals crucial insights into the statistical behavior of individual matrix entries after low-rank approximation, filling a gap in existing knowledge. A key contribution is a delocalization result for kernel matrix eigenvectors, derived using techniques from Random Matrix Theory. This result is particularly important because it addresses the challenge posed by non-zero mean, dependent entries in kernel matrices, which is usually not addressed by existing literature. Overall, the use of entrywise error bounds presents a powerful analytical framework for assessing the reliability and performance of low-rank matrix approximations, leading to a more nuanced understanding of the approximation quality and making it relevant to practical applications.

Kernel Eigenvector Decay

#

The rate of decay in the eigenvalues of a kernel matrix, often referred to as ‘kernel eigenvector decay’, is a crucial concept with significant implications for machine learning. Faster decay implies that a low-rank approximation of the kernel matrix will be more accurate, because the information contained in the smaller eigenvalues is less significant. This has practical consequences for algorithm design; methods using low-rank approximations, like the Nystrom method or random features, become computationally efficient. The decay rate is also closely linked to the smoothness of the kernel function: smoother kernels tend to exhibit faster eigenvalue decay, a property that influences the generalization ability and sample complexity of learning algorithms. The type of decay (polynomial, exponential) and the rate parameter (α or β) heavily influence the choice of low-rank approximation method and the required rank to achieve a given level of accuracy. Understanding and characterizing kernel eigenvector decay is therefore essential for both theoretical analysis of kernel methods and development of efficient practical algorithms.

Random Matrix Theory

#

Random Matrix Theory (RMT) offers a powerful framework for understanding the spectral properties of large, random matrices. In the context of kernel matrices, RMT provides valuable insights, especially when dealing with high-dimensional data where traditional methods may falter. A key application is in establishing delocalization results for eigenvectors corresponding to small eigenvalues. This is crucial because it helps quantify the entrywise error bounds for low-rank approximations of kernel matrices, a common technique in machine learning. The inherent randomness of data often leads to a kernel matrix whose structure can be analyzed with RMT tools. Although kernel matrices often have non-zero means and dependent entries unlike the classic RMT models, the theoretical analysis leverages insights from RMT to derive novel concentration inequalities and bounds. This approach offers a principled way to tackle the statistical behavior of individual entries in low-rank approximations, a significant improvement over existing methods that focus solely on spectral or Frobenius norms. RMT’s role is to provide a foundation for proving eigenvalue and eigenvector concentration results, which are then instrumental in establishing entrywise error bounds.

Low-Rank Approx. Methods

#

Low-rank approximation methods are crucial for efficiently handling large datasets and high-dimensional data, which are prevalent in machine learning. These methods reduce the computational complexity and storage requirements by approximating a large matrix with a smaller matrix of lower rank, preserving essential information. The choice of low-rank approximation method depends on various factors, including the specific application, the structure of the data, and the desired accuracy-speed trade-off. Popular techniques include truncated singular value decomposition (SVD), which provides the optimal low-rank approximation in terms of Frobenius norm, and randomized SVD, which offers a faster approximation with provable error bounds. Other methods leverage specific data structures or properties, such as Nyström methods for kernel matrices or CUR decomposition. Accuracy and computational efficiency are key considerations, with many algorithms providing guarantees on the approximation error in relation to the rank of the approximation. The choice of rank itself involves a bias-variance trade-off, with higher ranks capturing more information but increasing computational cost.

High-Dimensional Limits

#

In high-dimensional settings, where the number of variables exceeds the number of observations, many traditional statistical methods fail. The curse of dimensionality manifests as increased computational complexity and a greater risk of overfitting. Analysis of high-dimensional data often requires different techniques, such as regularization, dimension reduction, or specialized algorithms designed to handle sparse data. Understanding the limitations of classical methods in high dimensions is crucial for selecting appropriate techniques and interpreting results. Careful consideration of asymptotic behavior is necessary since convergence rates may be slower, and the finite-sample performance might differ significantly from theoretical predictions. Robustness to noise becomes paramount, as high-dimensional data often contains more noise relative to signal. Finally, developing new theoretical frameworks tailored to high-dimensional scenarios is an active area of research to better quantify the behavior of statistical estimators and improve their performance.

More visual insights

#

More on figures

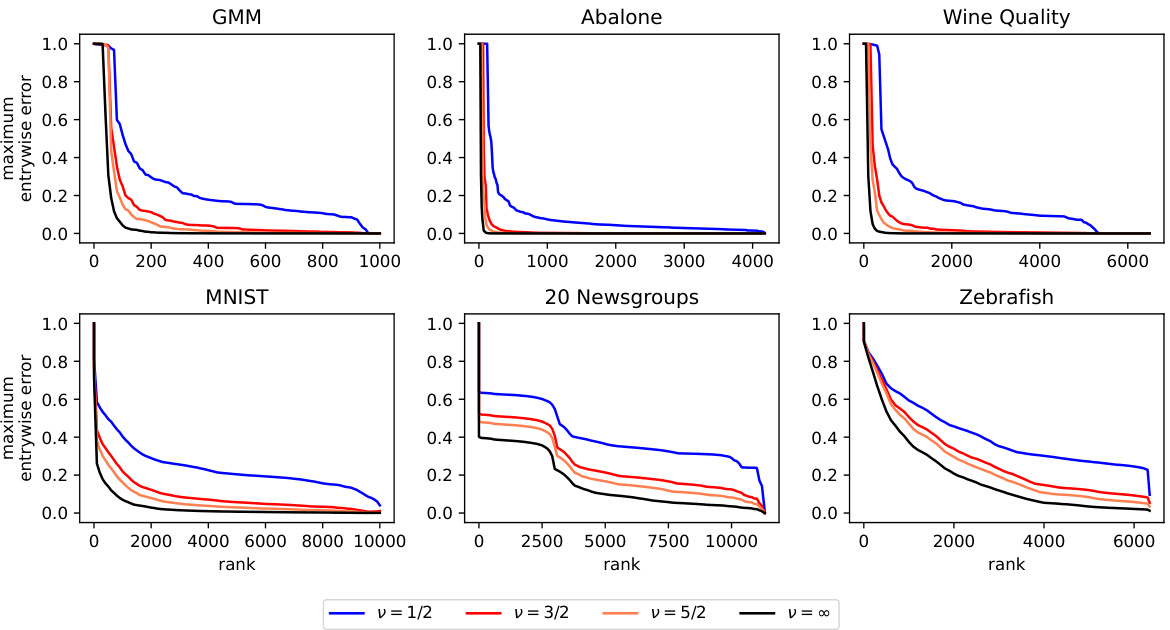
This figure shows the maximum entrywise error for low-rank approximations of kernel matrices for six datasets. Each dataset is represented in a separate subplot, and the different lines in each plot represent the use of different Matérn kernels with varying smoothness parameters (v = 1/2, 3/2, 5/2, ∞). The x-axis shows the rank of the approximation, and the y-axis shows the maximum entrywise error. The figure demonstrates how the maximum entrywise error decreases as the rank increases, and how this decay varies depending on the kernel smoothness and the dataset. Section 5 of the paper provides additional details about the experiments.

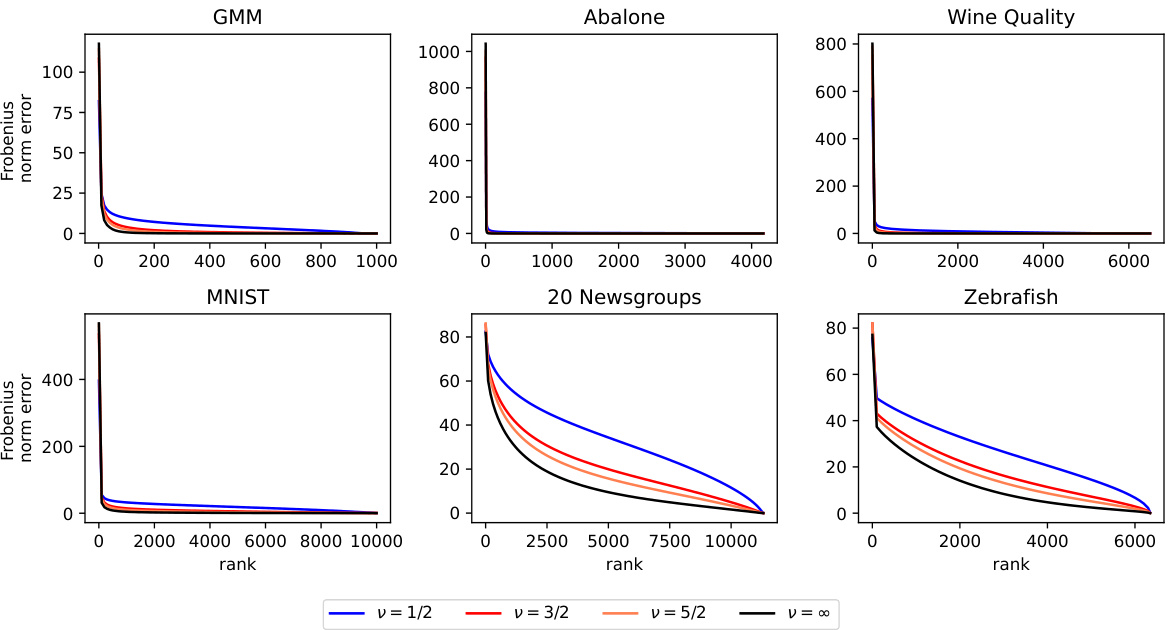
This figure compares the Frobenius norm error for different low-rank approximations of kernel matrices constructed from various datasets (GMM, Abalone, Wine Quality, MNIST, 20 Newsgroups, Zebrafish). Each dataset uses a Matérn kernel with varying smoothness parameters (v = 1/2, 3/2, 5/2, ∞). The x-axis represents the rank of the approximation, and the y-axis represents the Frobenius norm error. The plot shows how the error decreases as the rank increases, with the smoother kernels (larger v) showing faster convergence.

Full paper

#