↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Diffusion-based purification, a promising approach to enhance the robustness of deep neural networks against adversarial attacks, has been shown to be vulnerable to existing attack methods. The existing methods suffer from a gradient dilemma where global gradient averaging limits their effectiveness. Also, a single-attempt evaluation underestimates the risks associated with multiple attempts by an attacker.
To address these issues, this paper proposes DiffHammer, a novel attack method that selectively targets vulnerable purifications, incorporates N-evaluation to assess resubmit risks, and employs gradient grafting for efficient evaluation. Experimental results demonstrate that DiffHammer significantly outperforms existing state-of-the-art attack methods and highlights the limitations of diffusion-based purification defenses under resubmission attacks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it exposes critical vulnerabilities in existing diffusion-based adversarial purification methods. The proposed attack, DiffHammer, significantly impacts the field by providing a more effective evaluation method and highlighting the need for more robust defenses against resubmission attacks. This is particularly relevant in security-critical applications where even a single successful attack can have severe consequences. The findings open new avenues for research in developing more resilient and reliable purification techniques.
Visual Insights#

This figure illustrates the DiffHammer attack method. Panel (a) shows two sets of purifications: those with shared vulnerabilities (S1) and those with non-shared vulnerabilities (S0). Panels (b) and (c) demonstrate the gradient dilemma. Attacking purifications with both shared and non-shared vulnerabilities (S0 U S1) is less effective than focusing solely on the shared vulnerabilities (S1). Panels (d) and (e) illustrate the EM algorithm used in DiffHammer. The E-step identifies purifications with shared vulnerabilities (S1), and the M-step aggregates their gradients to improve attack effectiveness.
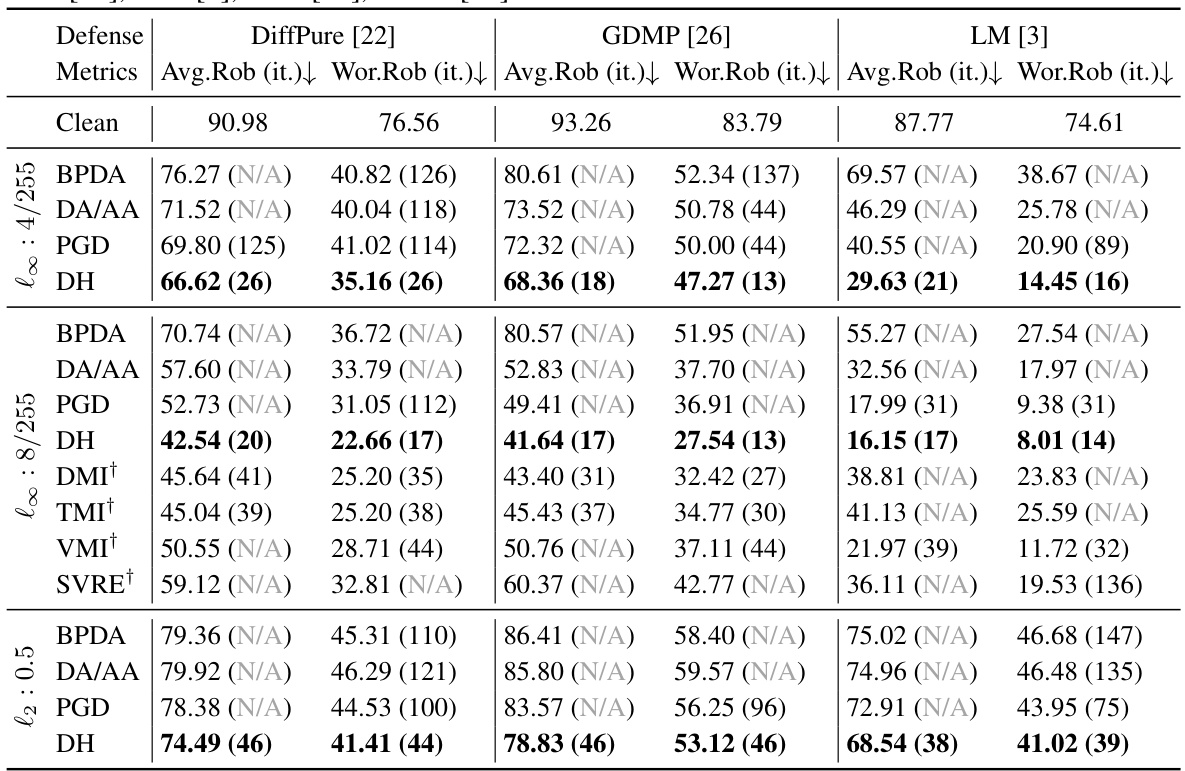
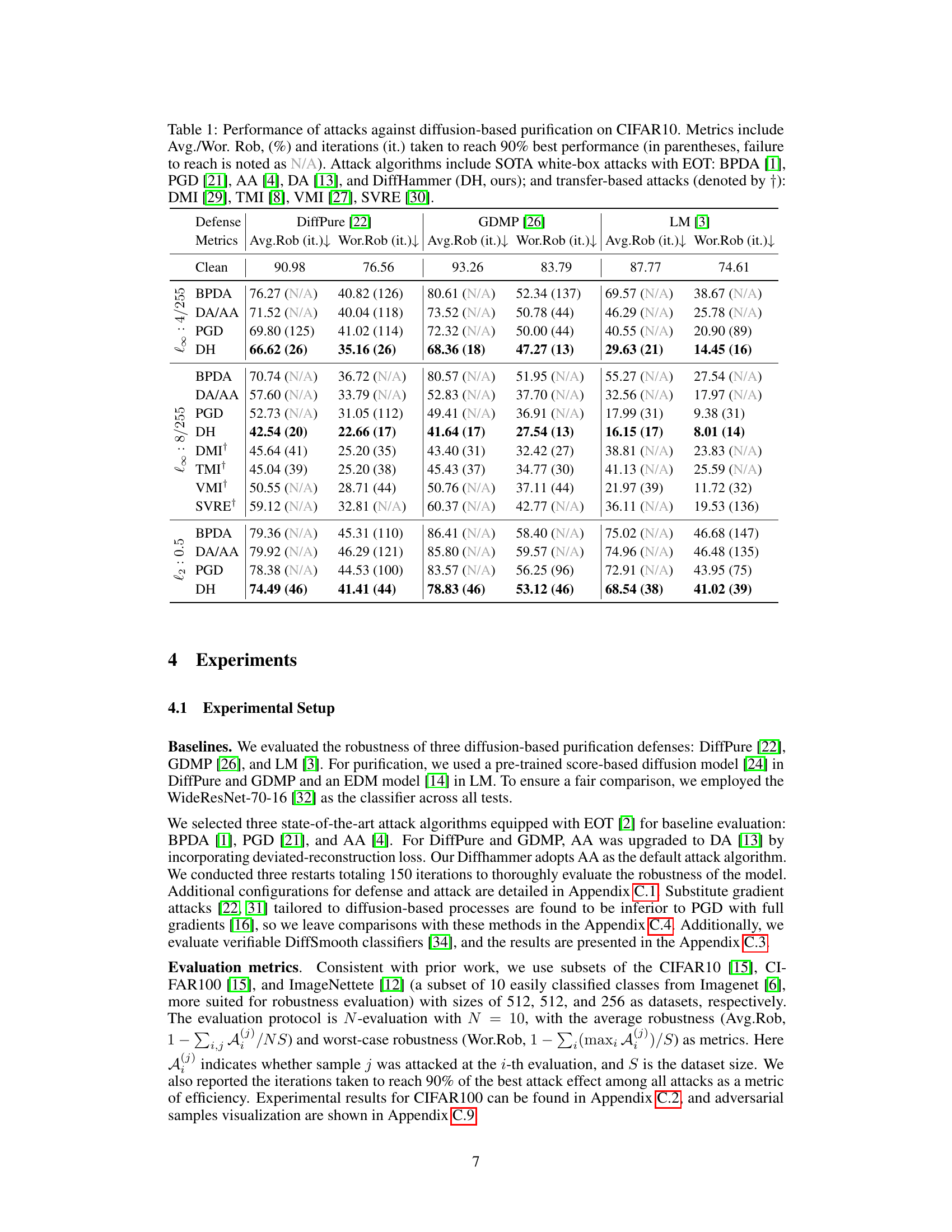
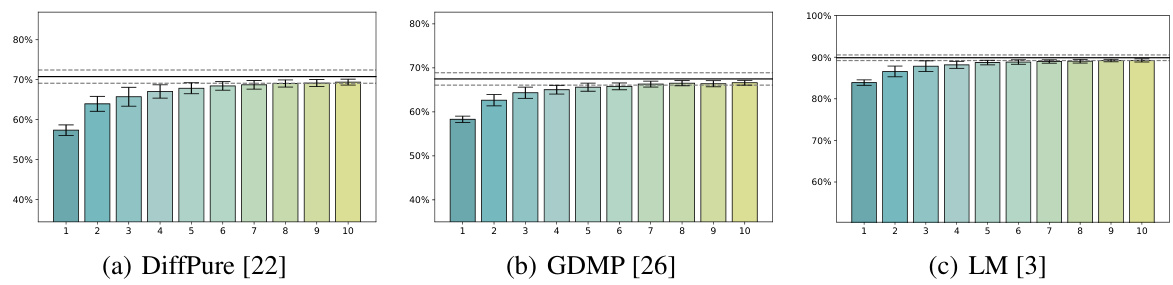
This table presents a comparison of various attack methods against three different diffusion-based purification defenses (DiffPure, GDMP, and LM) on the CIFAR-10 dataset. The table shows the average robustness (Avg.Rob), worst-case robustness (Wor.Rob), and the number of iterations it took for each attack to reach 90% of its best performance. Both white-box attacks (using Expectation of Transformation or EOT) and transfer-based attacks are included for comparison. The results highlight the effectiveness and efficiency of the proposed DiffHammer attack.
In-depth insights#
EOT Attack Limits#
The concept of “EOT Attack Limits” within the context of adversarial purification using diffusion models reveals crucial vulnerabilities in existing evaluation methods. Expectation of Transformation (EOT) attacks, while seemingly robust, suffer from a significant limitation: gradient dilemmas. These dilemmas arise from the global averaging of gradients across diverse purifications, where the heterogeneity in vulnerabilities among individual purifications leads to ineffective attacks. Consequently, relying solely on EOT-based attacks underestimates the true robustness of these models, generating a false sense of security. Addressing this shortcoming necessitates a shift towards more nuanced evaluation approaches. This might involve strategies such as selective targeting of vulnerable purifications and incorporating N-evaluation protocols to assess the risk of multiple attack attempts. A more sophisticated evaluation methodology is needed to better reflect the inherent stochasticity and iterative nature of diffusion-based purification.
DiffHammer Method#
The DiffHammer method is a novel approach to evaluating the robustness of diffusion-based adversarial purification. It addresses the gradient dilemma inherent in existing Expectation of Transformation (EOT) based attacks by selectively targeting purifications with shared vulnerabilities, thus improving attack efficiency. By incorporating N-evaluation, it provides a more comprehensive assessment of resubmit risk compared to 1-evaluation, which is insufficient for stochastic defenses. DiffHammer leverages gradient grafting to enhance efficiency, reducing backpropagation complexity from O(N) to O(1). The method’s effectiveness is validated through extensive experiments, demonstrating superior performance in circumventing the gradient dilemma and achieving near-optimal attack success rates within fewer iterations. The overall significance lies in its ability to expose weaknesses previously underestimated in diffusion-based purification, ultimately advancing the understanding and development of more robust adversarial defenses.
N-Eval Protocol#
The concept of an ‘N-Eval Protocol’ in the context of evaluating the robustness of diffusion-based adversarial purification methods is a significant advancement over traditional single-evaluation approaches. It directly addresses the inherent stochasticity of diffusion models, where a single adversarial attack might succeed or fail due to the inherent randomness in the purification process. By repeating the attack N times, N-Eval provides a more reliable estimate of the true robustness, offering a far more comprehensive and realistic assessment of the defense’s resilience. This is particularly important for attacks where even a single successful evasion (such as unauthorized login access) is considered a failure for the system. Furthermore, integrating N-Eval into the attack loop, as implied by the name, enables adaptive attacks that leverage the results of earlier attacks, effectively amplifying the effectiveness of the evaluation and highlighting weaknesses not apparent in single evaluations. The N-Eval Protocol moves beyond simply measuring success or failure rates, providing a robust statistical measure of the adversarial risk, thus enhancing the overall reliability of diffusion-based adversarial purification evaluation and improving the development of more robust defenses.
Gradient Grafting#
Gradient grafting, as presented in the context of this research paper, is a technique designed to significantly improve the efficiency of attacks against diffusion-based purification models. The core challenge addressed is the computational cost associated with evaluating gradients across numerous stochastic purifications. Gradient grafting bypasses this by cleverly approximating a weighted sum of full gradients using a much more efficient calculation involving approximate gradients. This approach leverages the Expectation-Maximization (EM) algorithm, specifically focusing on shared vulnerabilities across purifications, to identify and aggregate information from purifications most susceptible to an attack. By grafting low-cost approximate gradients onto a representative purification, backpropagation’s complexity is reduced dramatically, allowing for a comprehensive and efficient gradient aggregation within a reasonable time frame. The technique directly mitigates the computational bottleneck imposed by standard gradient aggregation methods, enabling more effective and speedy adversarial attacks against the diffusion-based systems. The success of gradient grafting is contingent upon the effectiveness of the EM algorithm in the selective identification of vulnerable purifications, emphasizing the importance of this underlying component in the overall effectiveness of the proposed attack.
Robustness Revisited#
A section titled “Robustness Revisited” in a research paper would likely delve into a critical re-evaluation of existing claims about a system’s resilience. It would probably start by summarizing the state-of-the-art in robustness metrics and evaluation methodologies, acknowledging common assumptions and limitations. The core of the section would then present new findings that challenge the previously accepted levels of robustness. This could involve introducing novel attack vectors, proposing refined evaluation criteria, or demonstrating vulnerabilities under previously unconsidered conditions. The discussion would need to carefully analyze the implications of these findings, possibly highlighting the limitations of existing defenses and suggesting directions for future research. A key aspect would be to quantify the extent of the robustness revision, providing a comparative analysis with prior results and clearly identifying any shifts in the understanding of the system’s resilience. It would ideally conclude with a discussion of broader implications for the field, emphasizing how this revised understanding affects the practical application and future development of the system.
More visual insights#
More on figures

This figure illustrates the DiffHammer algorithm, highlighting its selective attack strategy to overcome the gradient dilemma in diffusion-based purification. It shows how DiffHammer identifies purifications with shared vulnerabilities (S1) and avoids attacking purifications with unshared vulnerabilities (So) which leads to ineffective gradient updates. The E-step identifies S1 purifications, and the M-step aggregates their gradients for a more effective attack.
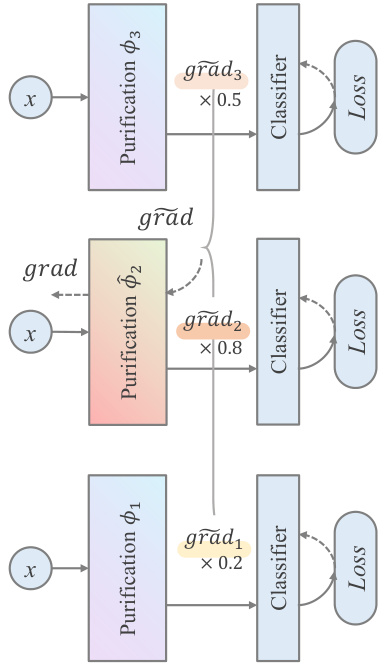
This figure illustrates the gradient aggregation method used in DiffHammer for efficiency. It shows three purifications (φ₁, φ₂, φ₃) applied to the input sample x, each followed by a classifier and loss calculation. The gradients from these purifications (grad₁, grad₂, grad₃) are weighted and aggregated before backpropagation. The weights (×0.2, ×0.8, ×0.5) show how the gradients are combined for a more efficient gradient estimate compared to computing gradients for all purifications individually.

This figure shows the distribution of attack success rates for different diffusion-based purification methods under two evaluation scenarios: 1-evaluation and 10-evaluation. The inner ring represents the results of a single attack attempt (1-evaluation), while the outer ring shows the results when an attack is allowed to be resubmitted up to 10 times (10-evaluation). A significant finding is that 32.6% to 46.3% of samples exhibit unshared vulnerabilities, meaning that different purifications have different vulnerabilities. This highlights the limitation of single-attempt (1-evaluation) as a measure of robustness, as it underestimates the risk when attackers can repeatedly try to find a weakness.
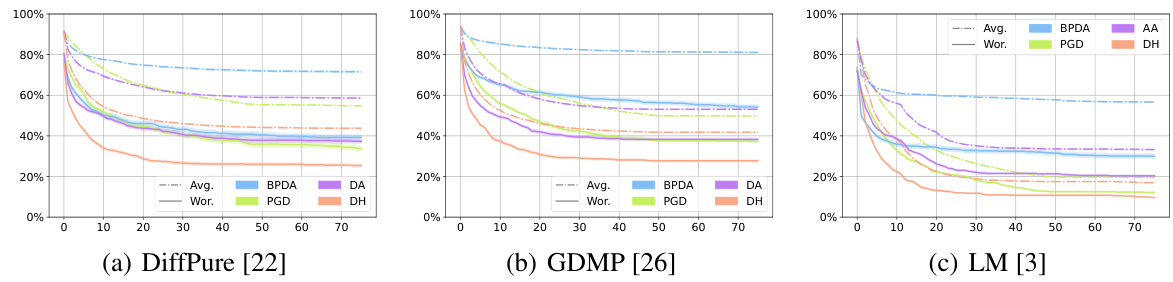
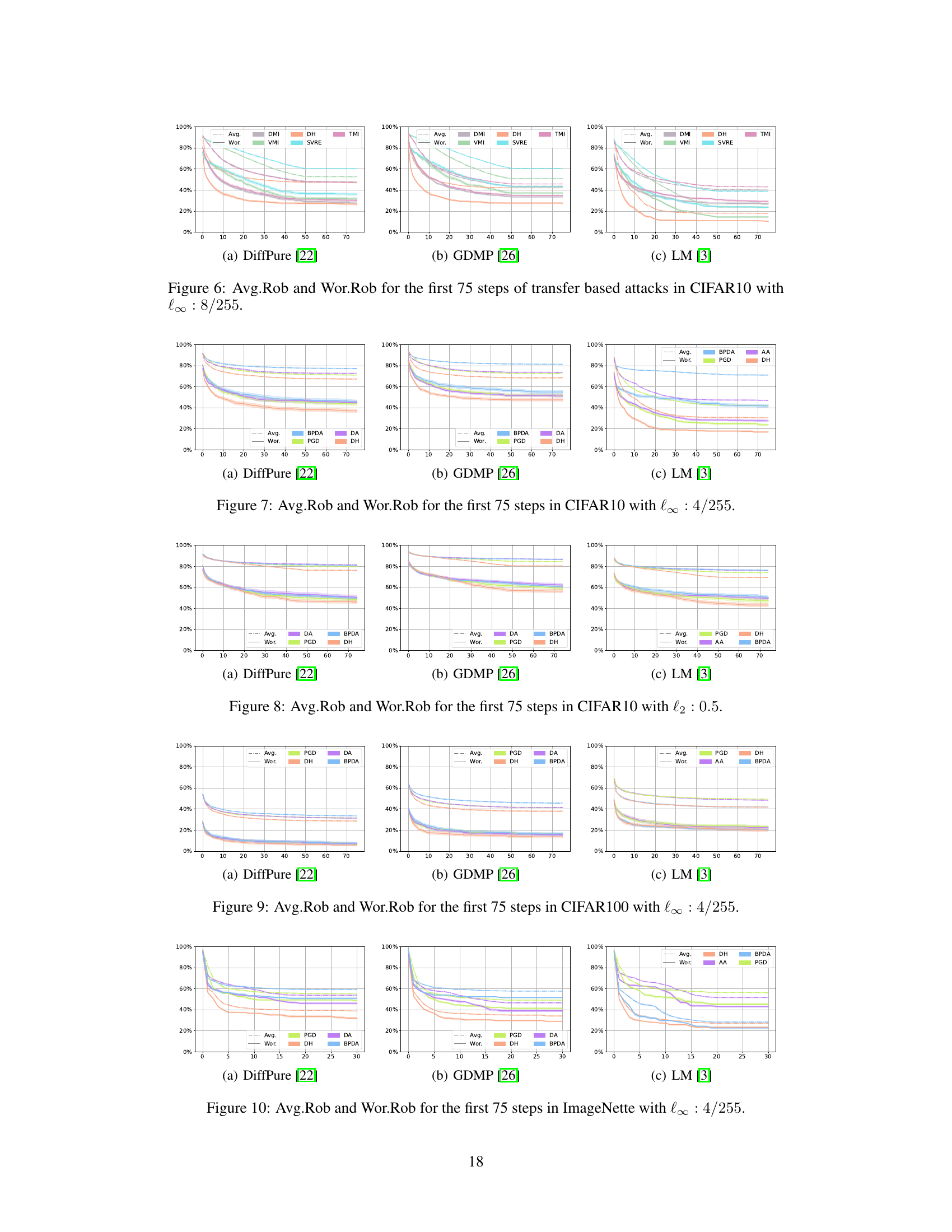
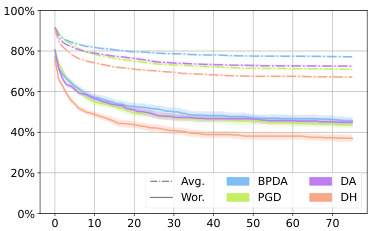
This figure displays the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) over the first 75 steps of different attack methods against three different diffusion-based purification defenses: DiffPure, GDMP, and LM. The x-axis represents the number of attack iterations, while the y-axis shows the robustness percentage. Each line represents a different attack algorithm (BPDA, DA, PGD, DH), and the colored lines distinguish between average and worst-case robustness for each method. The figure helps to visualize the effectiveness and efficiency of the different attack methods against each defense, highlighting the relative performance of DiffHammer (DH) compared to other state-of-the-art attacks.
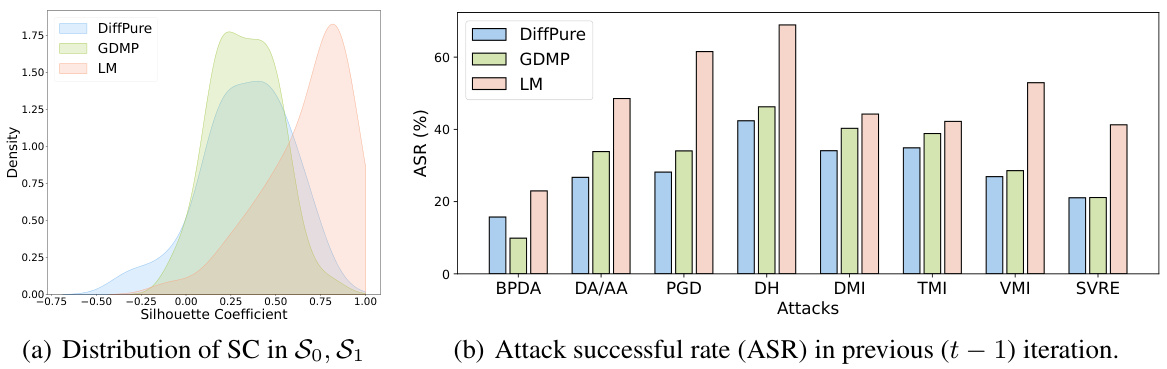
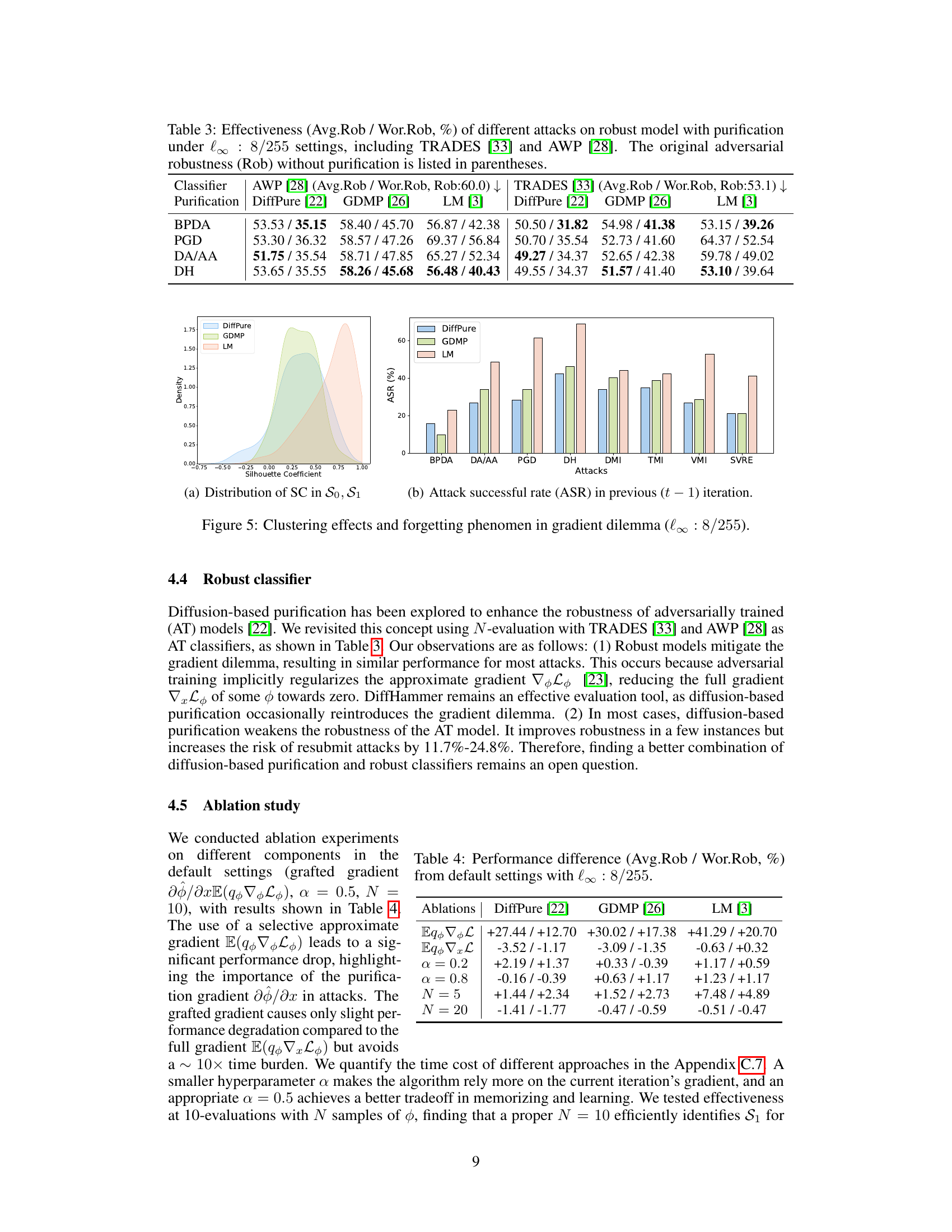
This figure visualizes the clustering effects and forgetting phenomenon observed in the gradient dilemma. The left subplot (a) shows the distribution of silhouette coefficients (SC) for gradients categorized into sets S0 (gradients with unshared vulnerabilities) and S1 (gradients with shared vulnerabilities), using cosine similarity. A clear separation between S0 and S1 suggests distinct gradient characteristics. The right subplot (b) illustrates the attack success rate (ASR) in the previous iteration (t-1) for different attacks. It highlights the consistency of DiffHammer’s attacks compared to other methods. The consistent ASR for DiffHammer across iterations indicates an effective strategy in mitigating the gradient dilemma.
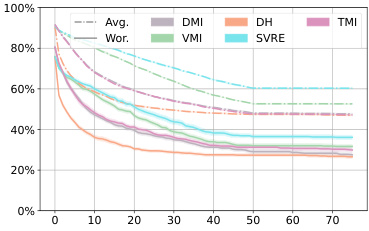
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, and LM) against various attack methods over the first 75 iterations. The l∞ norm is set to 8/255. It illustrates the effectiveness and efficiency of different attacks against these defense mechanisms.
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, and LM) against various attack algorithms (BPDA, DA/AA, PGD, and DiffHammer) over the first 75 steps. The l∞ norm is set to 8/255. The figure helps to visualize how the robustness of the purification methods changes over the iterations of the attacks and allows for comparison of different attack methods against the purification methods.
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, LM) against various attacks (BPDA, DA/AA, PGD, DH) over 75 steps. The l∞ norm constraint is set to 8/255, representing a small perturbation. The plot helps to visualize how the robustness of each defense changes over the course of the attack and how DiffHammer compares to other attack methods.
The figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for different attack methods (BPDA, DA, PGD, and DH) against three different diffusion-based purification defenses (DiffPure, GDMP, and LM) over the first 75 attack steps. The l∞ norm is set to 8/255. It illustrates the effectiveness and efficiency of DiffHammer compared to other attack methods.
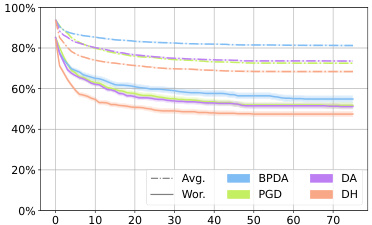
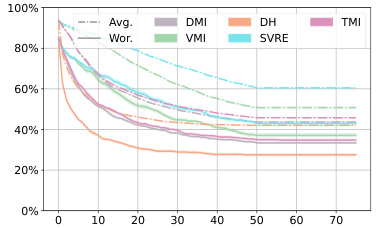
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, and LM) against several attack algorithms (BPDA, DA, PGD, and DiffHammer) over the first 75 steps of the attack process. The l∞ norm is set to 8/255. The curves illustrate how the robustness of each defense method changes as the attack progresses. It provides a visual comparison of the effectiveness and efficiency of different attack methods against these three purification techniques.
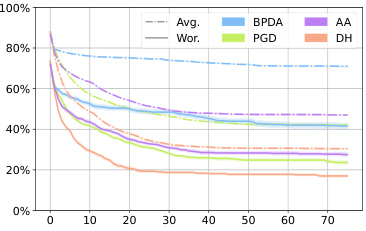
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) over the first 75 steps for different attack methods against three different diffusion-based purification methods (DiffPure, GDMP, and LM). The x-axis represents the number of attack iterations, and the y-axis represents the robustness percentage. The lines represent different attack algorithms (BPDA, AA, PGD, and DiffHammer). The figure helps to illustrate the relative effectiveness and efficiency of each attack method against the different purification techniques.
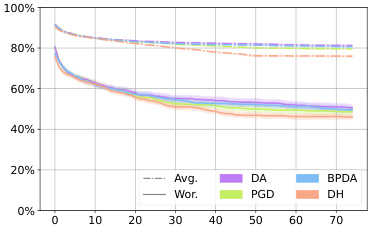
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, LM) against various attack algorithms (BPDA, DA, PGD, DH) over the first 75 attack steps. The l∞ norm is set to 8/255. The graph illustrates how the robustness of each purification method decreases as the number of attack iterations increases, and how DiffHammer generally achieves lower robustness values compared to other attack methods.
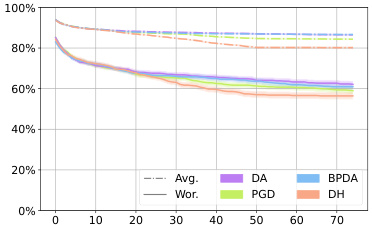
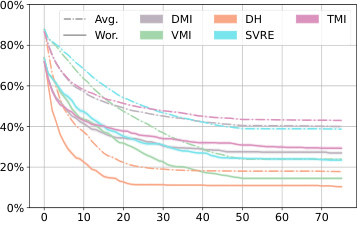
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification defenses (DiffPure, GDMP, LM) against various attack methods (BPDA, DA, PGD, DH) over the first 75 attack steps. The l∞ norm is set to 8/255. The curves illustrate how the robustness of each defense changes as the attacks progress.
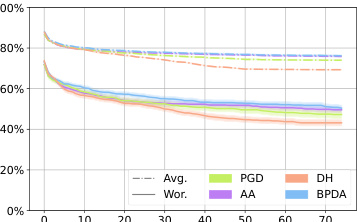
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for different attacks (BPDA, PGD, AA, and DiffHammer) against three different diffusion-based purification defenses (DiffPure, GDMP, and LM) over the first 75 steps of the attack process. The l∞ norm is set to 8/255. The graph allows for comparison of the effectiveness and efficiency of the attacks against the different defenses, highlighting the performance of DiffHammer.
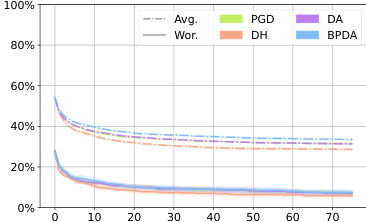
This figure presents the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, LM) across various attack algorithms (BPDA, PGD, DA, DH) over 75 iterations. The l∞ norm is set to 8/255. It visually demonstrates the effectiveness and efficiency of the DiffHammer attack, especially in comparison to other methods. The curves illustrate how the robustness of each defense decreases with increasing attack iterations.

This figure compares the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) of three different diffusion-based purification methods (DiffPure, GDMP, and LM) against various attacks (BPDA, PGD, DA, and DiffHammer) over 75 iterations. It shows how the robustness of each defense degrades as the number of attack iterations increases. The different line styles represent different attacks. The figure helps to visualize the effectiveness and efficiency of the proposed DiffHammer attack compared to existing attacks.
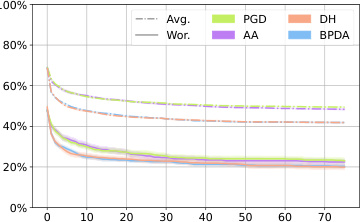
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, LM) against various attack algorithms (BPDA, PGD, AA, DH) over the first 75 steps. The l∞ norm is set to 8/255. The plot illustrates how the robustness of each purification method changes as the attack progresses. It helps to visualize the relative effectiveness and efficiency of each attack method against different purification techniques.
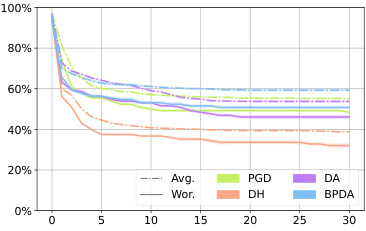
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for three different diffusion-based purification methods (DiffPure, GDMP, and LM) against various attack methods (BPDA, PGD, DA, and DiffHammer) over the first 75 steps of the attacks. The l∞ norm constraint is set to 8/255. The graph helps to visualize the effectiveness and efficiency of different attacks against these defense mechanisms, showing how robustness changes over time.
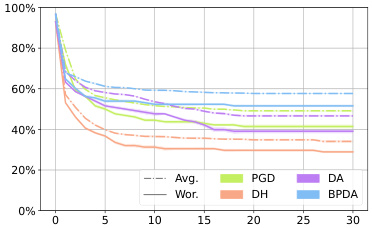
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for different attack methods (BPDA, AA, PGD, DH) against three different diffusion-based purification defenses (DiffPure, GDMP, LM) over the first 75 steps. The l∞ norm is set to 8/255. It helps visualize the effectiveness and efficiency of different attack methods in reducing the robustness of diffusion-based purification.
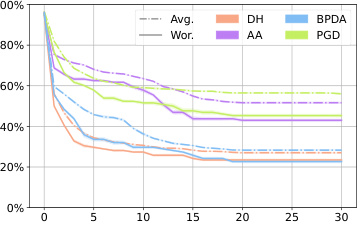
This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for different attack methods against diffusion-based purification. The x-axis represents the number of iterations, and the y-axis represents the robustness percentage. The lines show that DiffHammer achieves a higher attack success rate (lower robustness) faster than other methods.
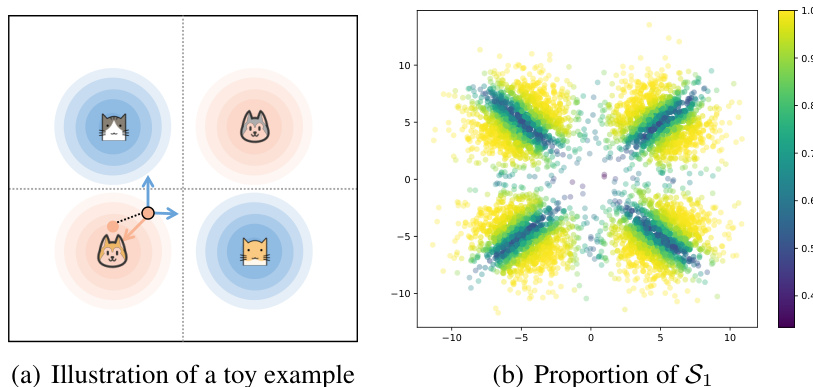
This figure illustrates a toy example to demonstrate the gradient dilemma. Panel (a) shows a simplified two-dimensional data distribution with four clusters representing different classes. The purification process is represented by a vector field that pulls samples slightly towards the center before diffusing them back to the data distribution. The samples are colored in panel (b) based on the proportion they belong to the set S1 (those with shared vulnerabilities). The colorbar indicates a higher proportion of samples belonging to S1, showing where the attack is most effective and where there is a gradient dilemma.

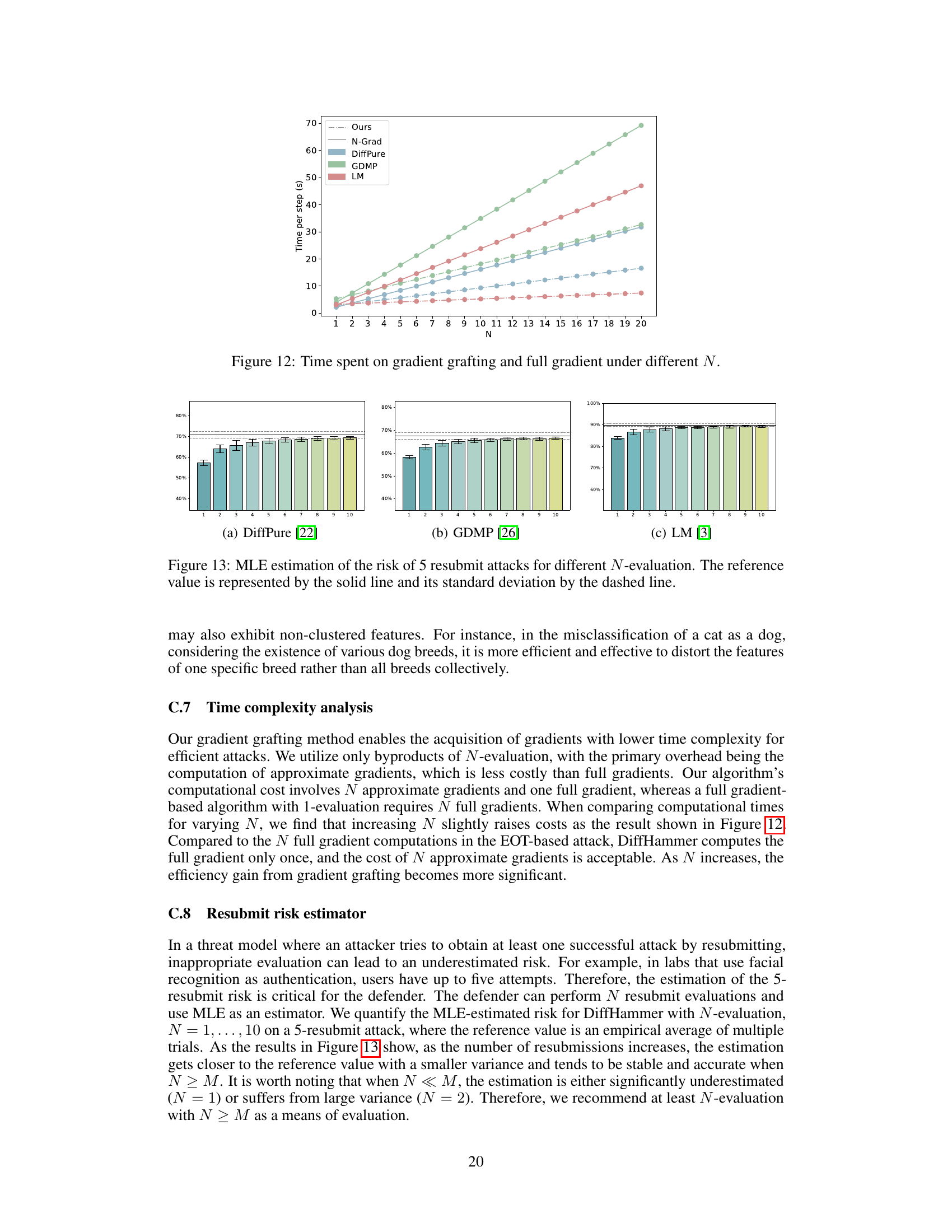
This figure shows the time (in seconds) spent per step for different methods (Ours, N-Grad, DiffPure, GDMP, LM) while varying the number of samples (N) used in the evaluation. The ‘Ours’ method represents the proposed DiffHammer approach, which employs gradient grafting for efficiency. ‘N-Grad’ refers to the baseline method that uses full gradients for all N samples. The figure illustrates that the proposed gradient grafting significantly reduces computational time, especially as N increases, showing a clear advantage of the DiffHammer approach over the baseline.
This figure shows the distribution of attack success rates for different diffusion-based purification methods under two evaluation scenarios: 1-evaluation and 10-evaluation. The inner ring represents the results of a single attack attempt (1-evaluation), while the outer ring shows the results after 10 consecutive attempts (10-evaluation). A significant finding is that a substantial portion (32.6% - 46.3%) of the samples exhibit vulnerabilities that are not shared across multiple purification attempts (unshared vulnerabilities). This highlights a critical limitation of 1-evaluation, which underestimates the risk of an attacker repeatedly submitting adversarial samples to exploit these unshared vulnerabilities.

This figure shows examples of adversarial samples generated by DiffHammer against DiffPure on the CIFAR10 dataset using an l∞ norm with a perturbation budget of 4/255. Each image shows an original correctly classified sample and the corresponding adversarially perturbed sample that is misclassified. The original label is shown in green and the adversarial (incorrect) label is shown in red. This illustrates the effectiveness of DiffHammer in generating nearly imperceptible perturbations that cause misclassification.

This figure shows examples of adversarial samples generated by DiffHammer on the CIFAR-10 dataset with an l∞ perturbation of 4/255. Each image pair shows the original image with its correct label in green and the adversarially perturbed image with its misclassified label in red, demonstrating the effectiveness of DiffHammer in generating imperceptible yet successful adversarial examples.

This figure shows examples of adversarial samples generated by DiffHammer on CIFAR10 with an adversarial perturbation of 4/255. Each image pair shows an original image and the corresponding adversarially perturbed image. The original label is shown in green, while the adversarial label is shown in red. This visualization demonstrates the effectiveness of DiffHammer in generating imperceptible perturbations that cause misclassification.

This figure shows the results of clustering the gradients into two sets (S0 and S1) using cosine similarity. The left panel shows the distribution of silhouette coefficients, indicating a significant difference between the gradients in the two sets. The right panel shows the attack success rate (ASR) in the previous iteration (t-1), demonstrating that the gradients in the two sets differ significantly. The gradient dilemma leads to ‘attack forgetting,’ where the effects of previous attacks are forgotten due to inconsistent gradients. DiffHammer avoids this by targeting shared vulnerabilities.

This figure shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) for different attack methods against three different diffusion-based purification models (DiffPure, GDMP, LM) on ImageNette dataset, using an l∞ norm constraint of 4/255. The x-axis represents the number of attack steps (iterations), and the y-axis shows the robustness percentage. It illustrates how the robustness of each model decreases over the course of multiple attack iterations for the different attack methods (BPDA, DA/AA, PGD, DH).
More on tables
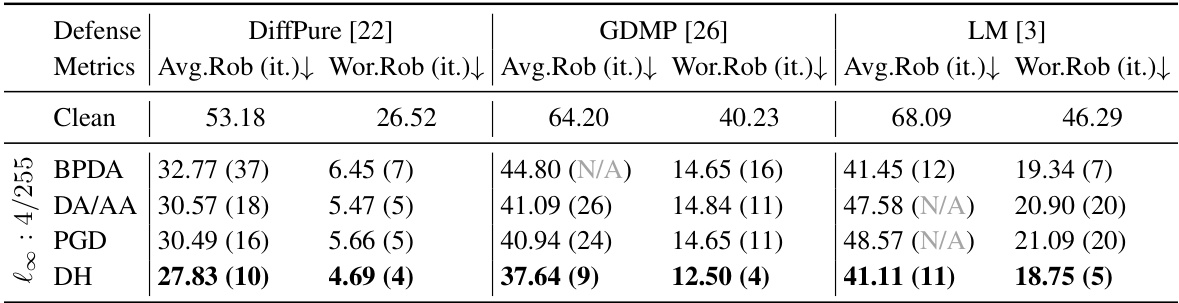
This table presents the results of various attacks against three different diffusion-based purification methods (DiffPure, GDMP, and LM) on the ImageNette dataset. It shows the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) achieved by each defense against several state-of-the-art attacks (BPDA, DA/AA, PGD, and DiffHammer). The numbers in parentheses indicate the number of iterations taken to reach 90% of the best attack performance. The table allows for a comparison of the effectiveness and efficiency of different attacks against each purification method.

This table presents the average and worst-case robustness (Avg.Rob/Wor.Rob) of three robust models (AWP, TRADES) against different attacks under 8/255 l∞ setting. Each robust model is tested with three different purification methods (DiffPure, GDMP, LM) and four different attack methods (BPDA, PGD, DA/AA, DH). The original robustness of the model without purification is included for comparison.
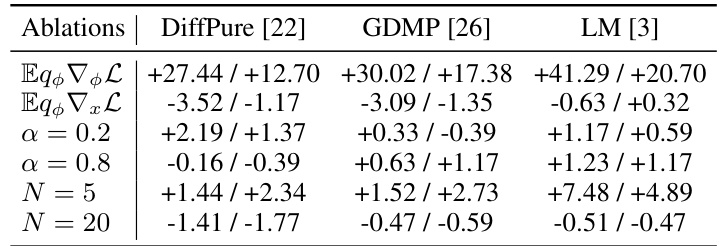
This table presents the results of an ablation study conducted to evaluate the impact of different components of the DiffHammer algorithm on the average and worst-case robustness of three different diffusion-based purification methods (DiffPure, GDMP, and LM). The ablation study varies the following components: using only approximate gradients (Eqφ), using only the full gradients (Eqx), the hyperparameter α (controlling gradient interpolation), and the number of resubmissions N (for N-evaluation). The values shown represent the difference in average robustness (Avg.Rob) and worst-case robustness (Wor.Rob) compared to the default setting of the DiffHammer.
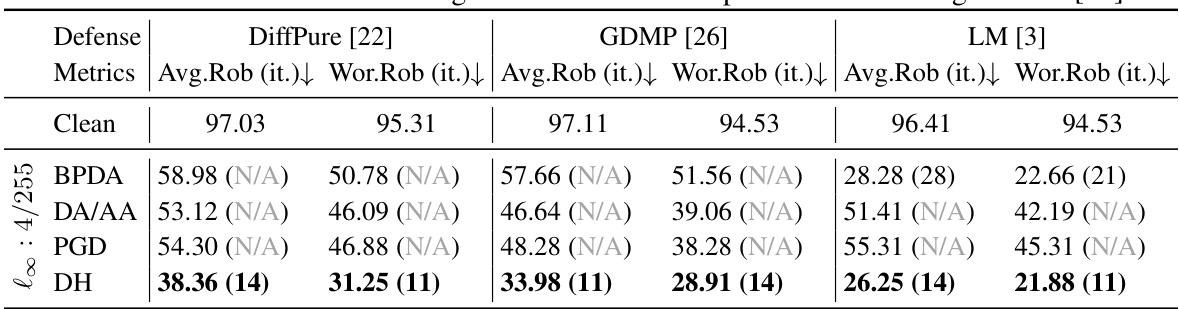
This table presents the results of various attacks against three different diffusion-based purification methods (DiffPure, GDMP, and LM) on the CIFAR100 dataset. The metrics used to evaluate the attacks are Average Robustness (Avg.Rob) and Worst-case Robustness (Wor.Rob), both expressed as percentages. The number of iterations (it.) taken by each attack to reach its best performance is also reported. The table shows the performance of different attacks, including BPDA, DA/AA, PGD and DiffHammer (DH), against each defense. N/A indicates that the attack did not reach 90% best performance within 150 iterations.
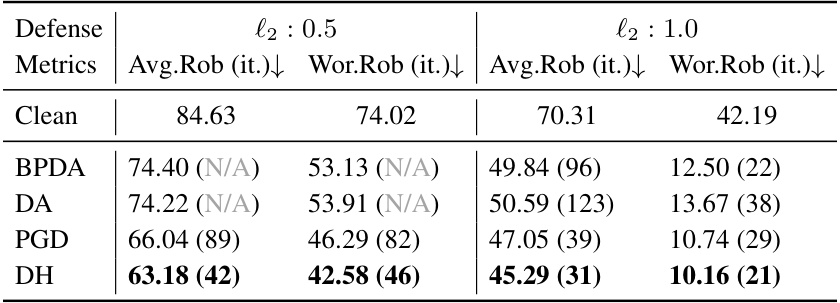
This table presents the results of various attacks against the DiffSmooth defense on the CIFAR10 dataset. The attacks are evaluated under two different l2 settings (l2: 0.5 and l2: 1.0). The metrics shown are the average robustness (Avg.Rob) and worst-case robustness (Wor.Rob), along with the number of iterations (it.) taken to achieve 90% of the best performance for each attack method. The attacks used include BPDA, DA, PGD, and DiffHammer (DH).
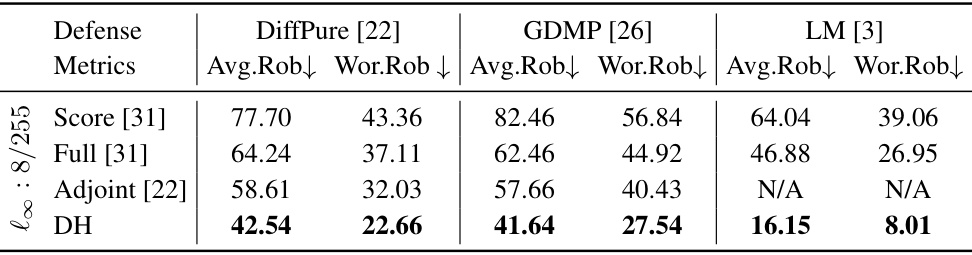
This table presents the results of various substitute gradient-based attacks against three different diffusion-based purification methods (DiffPure, GDMP, and LM) on the CIFAR10 dataset. The attacks used are Score [31], Full [31], Adjoint [22], and DiffHammer (DH). The metrics shown are Average Robustness (Avg.Rob) and Worst-case Robustness (Wor.Rob), both represented as percentages. Lower values indicate more effective attacks.
Full paper#