↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Causal inference struggles with the lack of realistic, complex benchmark datasets for method validation. Existing methods often fall short in precisely controlling essential causal properties like the marginal causal effect, especially when dealing with intricate real-world data patterns. This limits the development of robust and reliable causal inference techniques.
This paper introduces Frugal Flows, a novel likelihood-based model using normalizing flows to address these issues. Frugal Flows directly infer marginal causal quantities from observational data, enabling the creation of synthetic datasets that closely match empirical data while exactly satisfying user-defined causal constraints, including the degree of unobserved confounding. This method represents a significant advance in causal inference validation by allowing for more rigorous testing of methods under realistic conditions and customized causal properties.
Key Takeaways#
Why does it matter?#
This paper is crucial for causal inference researchers as it introduces Frugal Flows, a novel method for generating realistic synthetic datasets with customizable causal properties. This allows for robust validation of causal methods, addressing limitations of existing approaches and enabling more reliable inference. The exact parameterization of the causal margin, particularly for binary outcomes, is a significant advance. This methodology offers researchers a new tool to enhance the reliability and generalizability of their causal studies, expanding the potential for innovation in this critical area of research.
Visual Insights#
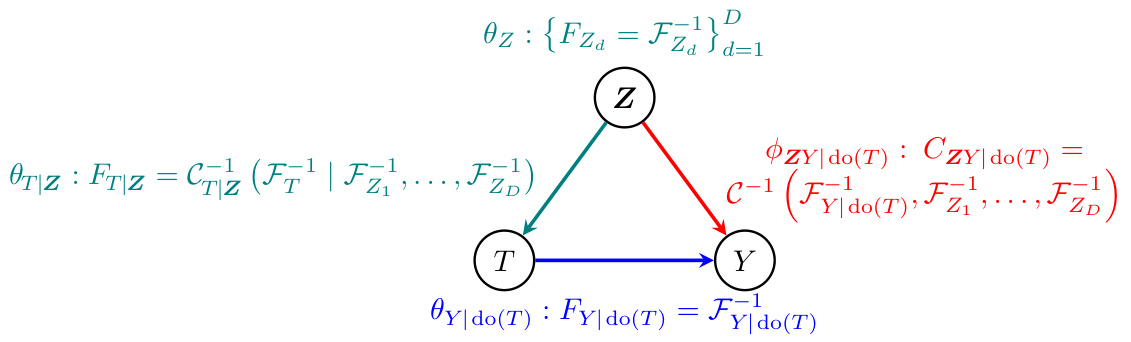
This figure illustrates the components of a frugal model and how each is parameterized. It shows how univariate and copula flows are used to model the marginal causal effect, the intervened dependency measure, and the past (pretreatment covariates and treatment).
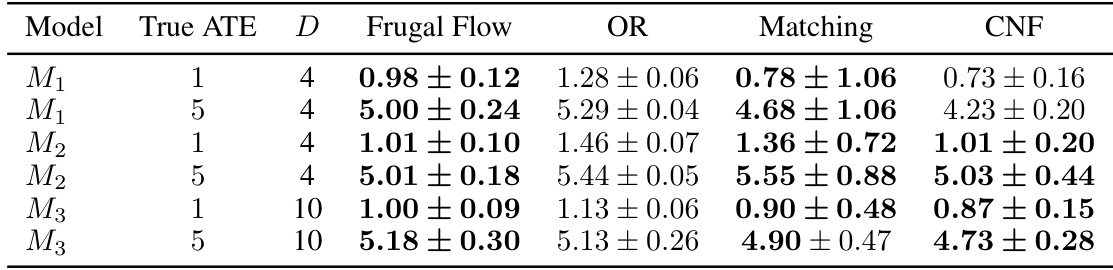
This table presents the results of Average Treatment Effect (ATE) estimation using four different methods: Frugal Flows, Ordinary Regression (OR), Matching, and Causal Normalizing Flows (CNF). The table shows the mean and 95% confidence interval of the estimated ATE for six different simulated datasets (three models with two different true ATE values each). The number of covariates in each dataset is also provided. Bold confidence intervals indicate that the true ATE is contained within the estimated range.
In-depth insights#
Frugal Flows Model#
The Frugal Flows model presents a novel approach to causal inference, leveraging the flexibility of normalizing flows to learn complex data-generating processes while directly inferring marginal causal quantities. This likelihood-based machine learning model is particularly useful for creating synthetic datasets to validate causal methods, offering a significant improvement over existing soft-constraint optimization techniques. A key advantage is its ability to exactly parameterize quantities like the average treatment effect and the degree of unobserved confounding, avoiding the need for post-hoc checks. The model’s flexibility extends to handling various outcome distributions and incorporating user-defined causal constraints, making it a versatile tool for causal benchmarking and validation. Its use of copula flows further enhances its capability to model complex dependencies and generate realistic synthetic data. Overall, Frugal Flows offers a powerful approach to address the limitations of current causal inference methods by combining flexibility with precise control over causal parameters.
Causal Inference#
Causal inference, aiming to establish cause-and-effect relationships from data, is a core topic. The paper highlights challenges in this field, particularly the difficulty of simulating realistic datasets with specified causal effects for model validation. Existing methods often lack flexibility or fail to accurately reproduce real-world data complexities. The authors propose Frugal Flows, a novel model leveraging normalizing flows for flexible data representation and precise causal parameterization. This allows for generating synthetic datasets closely resembling empirical data while exactly satisfying user-defined causal constraints, such as average treatment effects and the level of unobserved confounding. Frugal Flows offer a significant advancement by enabling direct control over causal margins during data generation, facilitating robust validation and benchmarking of causal inference methods. The approach is shown to outperform existing methods across various simulated and real-world datasets.
Benchmark Datasets#
Benchmark datasets are crucial for evaluating causal inference methods, yet creating realistic and informative ones is challenging. Existing datasets often lack the complexity of real-world scenarios, hindering the development of robust methods. A key issue is ensuring that the datasets accurately reflect the desired causal relationships, including the degree of unobserved confounding. Generative models offer a promising solution, allowing researchers to create synthetic data with tailored properties, but many struggle to control the marginal causal effect precisely. The development of novel generative models that overcome these limitations, such as those described in this paper, is vital for advancing the field. By allowing researchers to specify exact causal margins, the resulting datasets enable more rigorous validation and a deeper understanding of causal relationships in complex settings. The ability to customize the amount of confounding makes them even more useful for evaluating the robustness of various causal inference techniques.
Copula Flows#
Copula flows represent a powerful technique for modeling complex, high-dimensional data by combining the flexibility of normalizing flows with the ability of copulas to capture intricate dependencies between variables. Normalizing flows excel at learning flexible data representations and transformations, while copulas allow modeling dependencies separately from marginal distributions. The fusion of these concepts allows for the creation of generative models capable of capturing nuanced relationships in complex datasets, as demonstrated by the authors in their use of copula flows within Frugal Flows for causal inference. This approach offers a significant advantage for validation and benchmark creation, enabling the generation of realistic synthetic datasets that accurately reflect desired properties, including specified causal relationships and degrees of unobserved confounding. A key strength lies in the ability to disentangle and explicitly parameterize the marginal causal effect, a feature absent in many conventional methods. This unique capability enhances both the accuracy and interpretability of causal inference models built upon these generated datasets.
Future Research#
Future research directions for Frugal Flows could focus on enhancing the model’s scalability and efficiency for larger datasets. Addressing the computational intensity of hyperparameter tuning is crucial for wider applicability. Exploring alternative copula modeling techniques, potentially reducing reliance on neural networks, could improve performance, especially with smaller datasets. Investigating the impact of the dequantization mechanism on discrete variable handling and exploring alternative methods for preserving data structure warrant further research. Extending the model’s capability to handle various data types, particularly categorical variables, while maintaining the exact marginal parameterization is important. Finally, applying Frugal Flows to a wider range of real-world datasets with diverse causal structures, and carefully evaluating its robustness against model misspecification, are crucial steps toward establishing its reliability and general applicability.
More visual insights#
More on figures
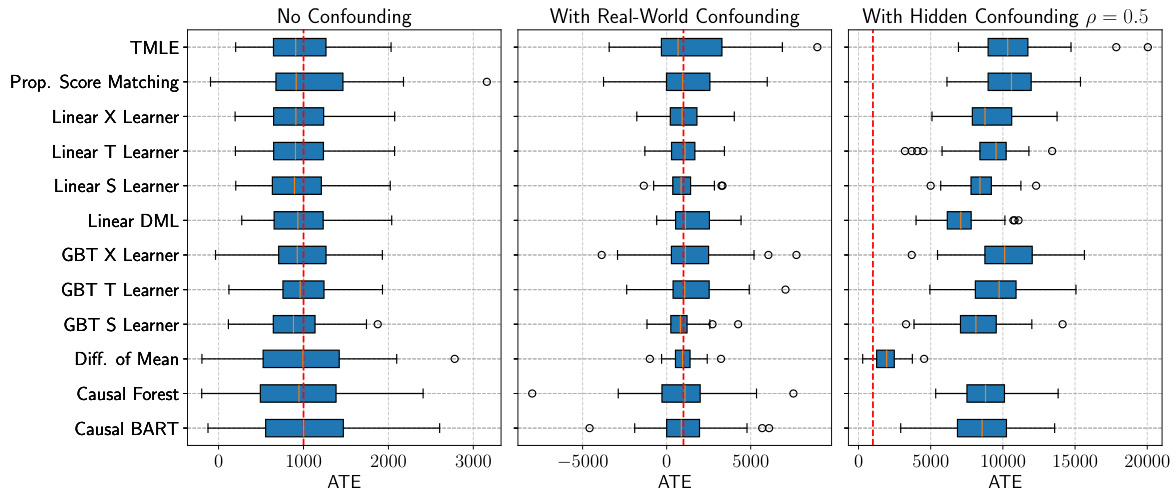
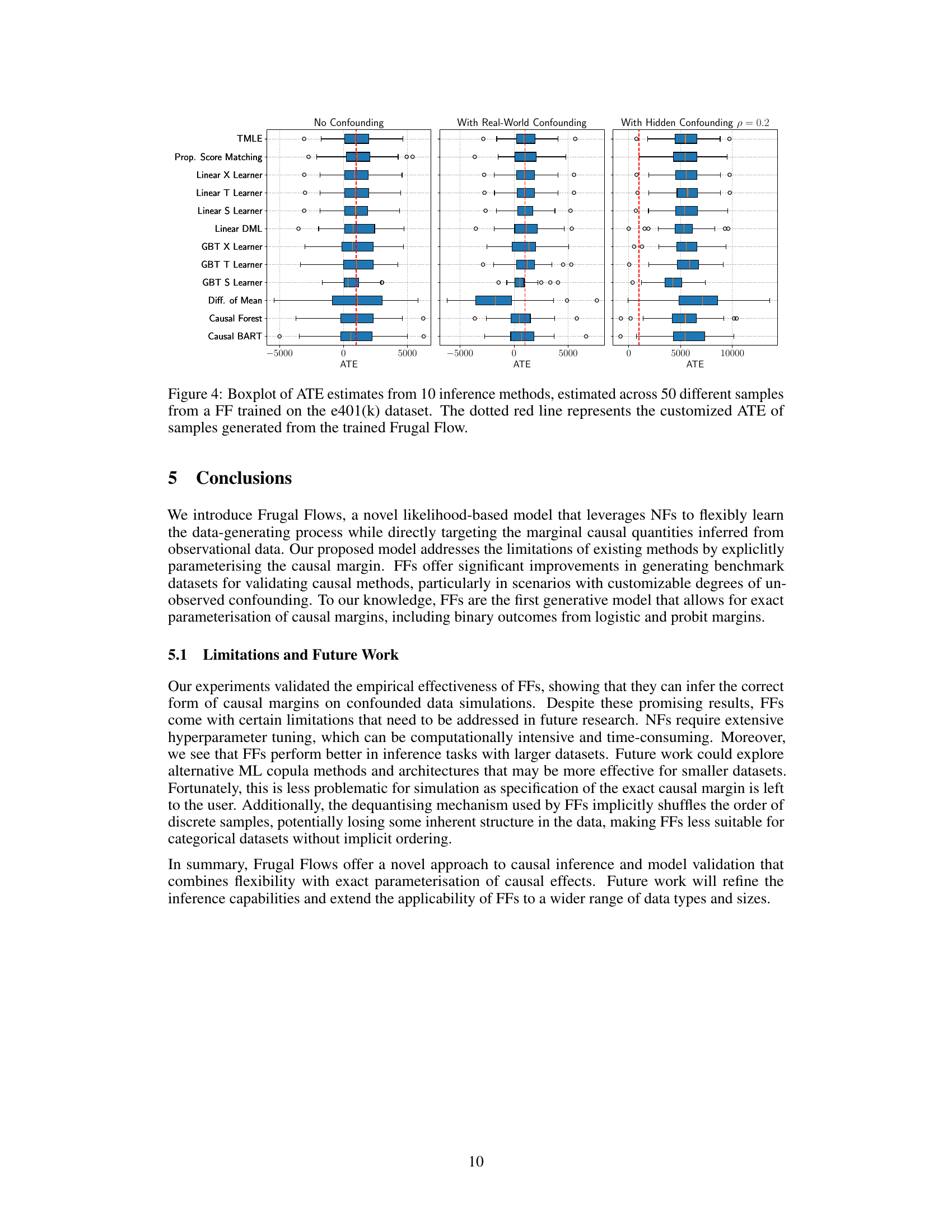
Boxplots showing the distribution of Average Treatment Effect (ATE) estimates from ten different causal inference methods applied to 50 datasets generated from a Frugal Flow model trained on the Lalonde dataset. Each boxplot represents a method, showing the median, quartiles, and range of ATE estimates. The red dotted line indicates the true ATE programmed into the Frugal Flow model during data generation. This figure demonstrates the performance of various causal inference methods on data that mimics real-world complexity and confounding.
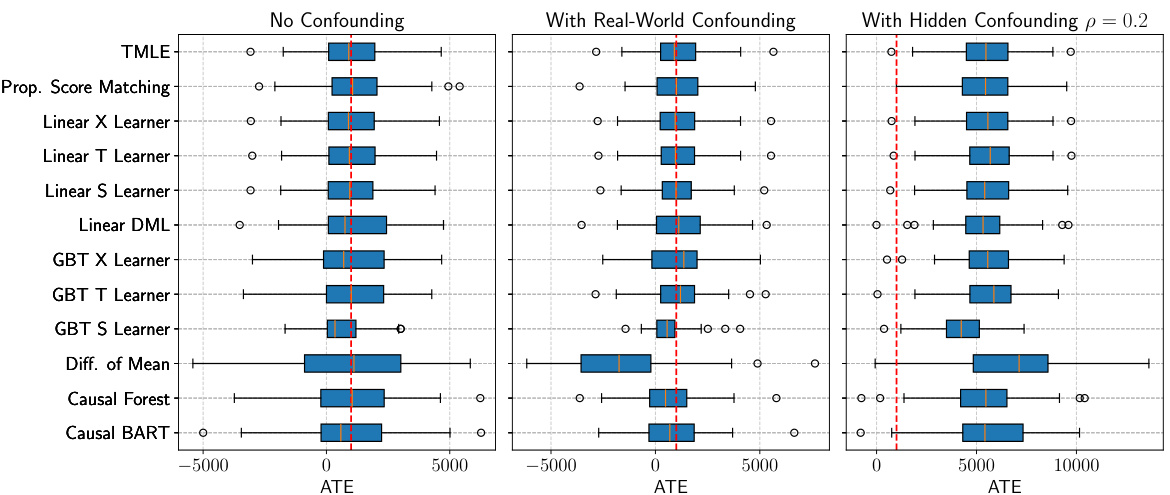
Boxplots showing the distribution of ATE estimates from 10 different causal inference methods applied to 50 synthetic datasets generated by a Frugal Flow trained on the e401(k) dataset. Three scenarios are shown: no confounding, real-world confounding, and hidden confounding with a correlation of 0.2. The red dotted line indicates the true ATE used to generate the synthetic data.
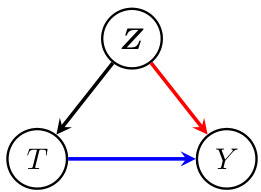
This figure shows a causal diagram representing a static causal treatment model. The variables are: T (treatment), Z (pre-treatment covariates), and Y (outcome). The black arrows depict the relationship between Z and T, where Z affects T, representing the data generation process prior to treatment assignment. The red arrow shows the direct effect of Z on Y, while the blue arrow represents the direct causal effect of T on Y. The model aims to estimate the marginal causal effect of T on Y, independent of Z. The crucial element is the dependency measure (ϕ) which relates Z and Y given the treatment T. This measure needs to be designed such that it does not change the marginal distributions of Z and Y, ensuring that any change only affects the dependence between them. This is vital for accurately representing the causal effect of T on Y.
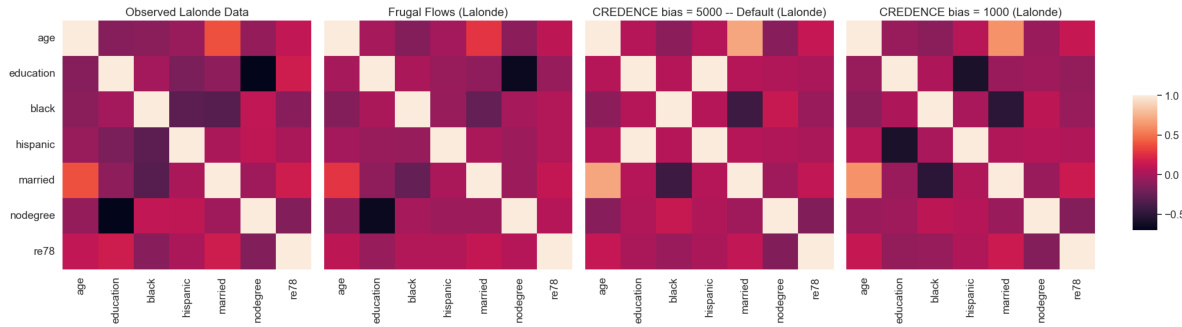
This figure compares the correlation matrices of the Lalonde dataset’s observed data with those generated by Frugal Flows and Credence models. It demonstrates how closely Frugal Flows reproduce the original data’s correlation structure, even when compared to models (Credence) which aim to exactly match specific causal constraints. The different columns illustrate how the correlations change when different causal effects are targeted.
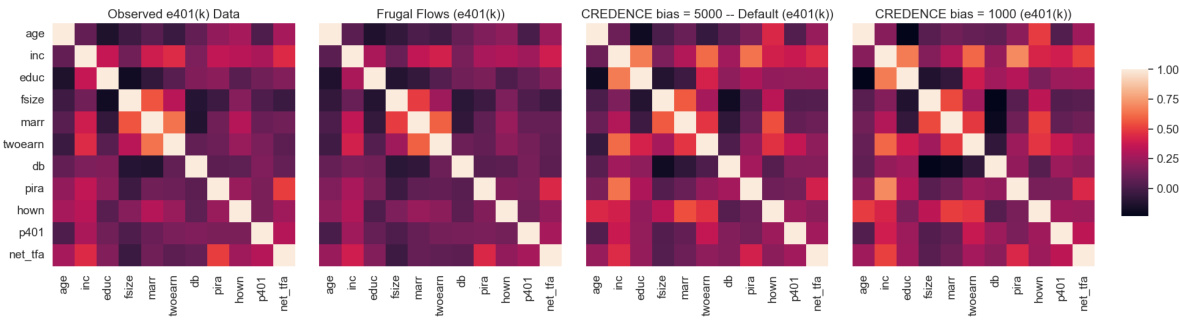
This figure compares the correlation matrices of the observed e401(k) dataset with those generated by Frugal Flows and Credence models. It highlights the ability of Frugal Flows to generate synthetic data that closely resembles the original data, even when adjusting causal constraints. In contrast, Credence shows a greater deviation in covariate dependencies when modifying causal constraints.
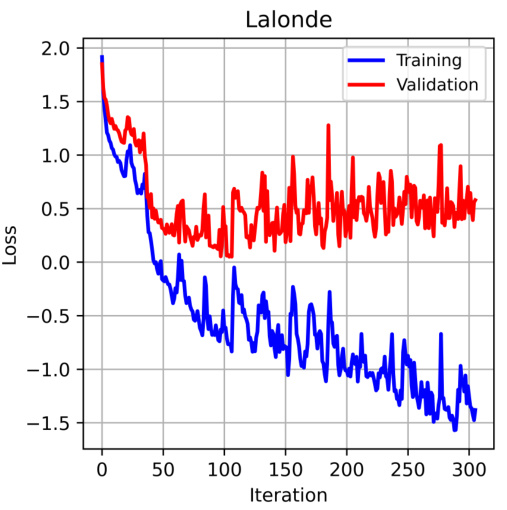
This figure shows the training and validation loss curves during the training of a Frugal Flow model on the Lalonde dataset. The x-axis represents the iteration number, and the y-axis represents the loss. The blue line shows the training loss, and the red line shows the validation loss. The plot illustrates how the model’s performance on both the training and validation sets improves over time, ultimately converging towards a low loss value. The use of a ‘patience’ parameter of 200 indicates that training stopped when the validation loss did not improve for 200 iterations, a common technique to avoid overfitting.
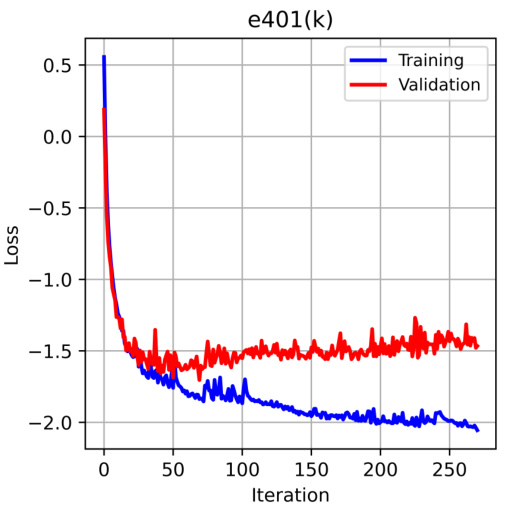
The figure shows the training and validation loss curves during the training process of a Frugal Flow model on the e401(k) dataset. The hyperparameters were optimized, and training stopped early using a patience criterion to prevent overfitting. The x-axis represents the training iteration, and the y-axis shows the loss value. The plot helps assess the model’s convergence and potential overfitting.
More on tables

This table presents the results of Average Treatment Effect (ATE) estimation using four different methods: Frugal Flow, Ordinary Least Squares regression, Matching, and Causal Normalizing Flow. The table compares the estimated ATEs across three different simulated data models with varying numbers of covariates, showing the performance of Frugal Flows against existing methods.

This table presents the results of the Average Treatment Effect (ATE) estimation using Frugal Flows, linear outcome regression (OR), matching, and causal normalising flows (CNF) for three different simulated datasets (M1, M2, M3). It shows the mean and 95% confidence interval of the estimated ATE across 25 runs for each method and model, along with the true ATE and number of covariates (D). Bold confidence intervals indicate that the true ATE is within the estimated range. The results highlight the performance of the different methods in recovering the true ATE under different levels of confounding and the number of covariates.
Full paper#