↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating the geometric transformation (homography) between images is crucial for many computer vision tasks, but existing unsupervised methods struggle with images from different sources (multimodal pairs), often requiring difficult-to-obtain ground truth data for supervised learning. This paper introduces a novel solution to improve the accuracy of unsupervised homography estimation, especially for multimodal image pairs.
The core of this solution is AltO, a novel framework which uses a two-phase alternating optimization to address the problem. The first phase reduces the differences in geometry between the two images (geometry gap), while the second phase tackles the differences in the image data itself (modality gap). Using two loss functions based on the Barlow Twins method, AltO shows superior performance to other unsupervised learning methods. The method is also shown to be compatible with a variety of network architectures.
Key Takeaways#
Why does it matter?#
This paper is important because it presents AltO, a novel unsupervised learning framework for homography estimation, particularly addressing the challenges of multimodal image pairs. This significantly advances the field by achieving results comparable to supervised methods, opening new avenues for applications needing robust image registration across varying modalities, such as image stitching and fusion. The framework’s independence from specific network architectures broadens its applicability and facilitates further research exploring different network designs and loss functions for improved performance.
Visual Insights#
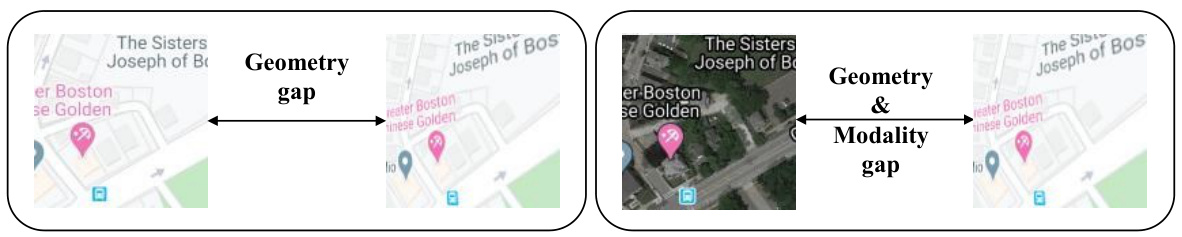
This figure shows examples of the two types of gaps addressed in the paper: the geometry gap and the modality gap. The geometry gap refers to the difference in geometric alignment between two images of the same scene, while the modality gap refers to differences in image representation (e.g., a map versus a satellite image of the same location). The image pairs shown are from the DLKFM dataset [11].
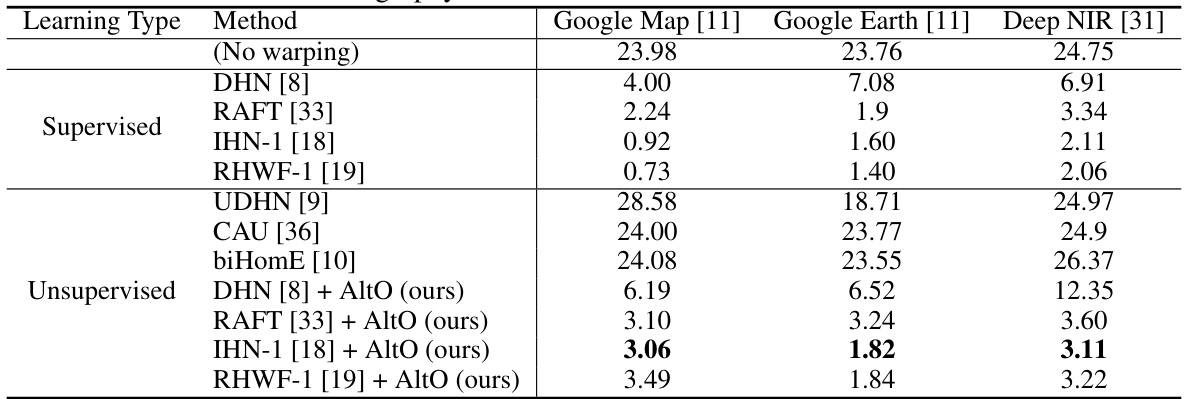
This table presents a comparison of the proposed AltO method’s performance against other supervised and unsupervised learning-based methods for homography estimation. The comparison uses three different multimodal datasets (Google Map, Google Earth, and Deep NIR) and evaluates the methods based on Mean Average Corner Error (MACE). The results demonstrate that AltO achieves state-of-the-art performance among unsupervised methods while exhibiting strong robustness across various network architectures.
In-depth insights#
Multimodal Homography#
Multimodal homography tackles the challenge of estimating the geometric transformation between image pairs from disparate modalities, such as satellite imagery and maps, or RGB and near-infrared images. Unlike traditional homography estimation methods that often assume similar image characteristics, multimodal homography must address significant variations in visual appearance and potentially different geometric distortions. This necessitates robust techniques that can handle large modality gaps, while still achieving accurate geometric alignment. Unsupervised learning is particularly relevant here, as ground truth data for multimodal image pairs is often scarce or expensive to acquire. Methods addressing this challenge frequently leverage metric learning, employing techniques that embed images from various modalities into a shared feature space where the geometric relationship is easier to learn. This approach necessitates robust loss functions capable of measuring similarity in the face of modality differences, and often involve sophisticated optimization strategies to disentangle the effects of modality and geometry.
AltO Framework#
The AltO framework, designed for unsupervised homography estimation on multimodal image pairs, presents a novel two-phase alternating optimization approach. This iterative process cleverly tackles both the geometry and modality gaps inherent in multimodal data. The first phase reduces the geometric gap using a Geometry Barlow Twins loss, an extended Barlow Twins loss tailored to address geometric discrepancies between images. The second phase focuses on minimizing the modality gap via the standard Barlow Twins loss. This alternating framework elegantly avoids the trivial solution problem often encountered in unsupervised learning, where the network collapses to a simple solution instead of learning meaningful representations. AltO’s effectiveness is demonstrated through its compatibility with various homography estimator architectures and superior performance on multimodal datasets, showcasing the framework’s versatility and robustness.
Geometry & Modality#
The concept of “Geometry & Modality” in unsupervised homography estimation highlights the dual challenge of aligning images from different sources. Geometric discrepancies arise from differences in camera viewpoints and transformations, requiring robust geometric alignment techniques. Modality differences, however, stem from variations in image acquisition methods (e.g., different sensors, lighting conditions, or domains). These differences in image appearance present unique challenges beyond pure geometry. Successfully addressing both aspects is crucial for robust and accurate homography estimation across diverse multimodal scenarios. A successful approach would likely require a two-pronged strategy that uses techniques such as feature matching (e.g., SIFT) for geometry, and metric learning approaches (e.g., Barlow Twins) for handling modality gaps. Combining these techniques in a unified framework, potentially using alternating optimization or similar strategies, is a key research direction to achieve accurate homography estimation on multimodal data, leading to improved performance in various applications such as image stitching and 3D reconstruction.
Ablation Study#
An ablation study systematically removes components of a machine learning model to assess their individual contributions. In the context of homography estimation, this would involve removing parts of the proposed AltO framework—such as the alternating optimization, the specific loss functions (Geometry Barlow Twins and Modality loss), or the global average pooling—to evaluate the impact on performance. The results of these experiments highlight the importance of each component, illustrating whether they contribute individually or synergistically. For instance, removing the alternating optimization might lead to the trivial solution problem, showcasing its crucial role in preventing model collapse. Similarly, comparing different loss functions reveals which is most effective for the geometry and modality gaps, helping to understand the algorithm’s design choices. Analyzing the impact of removing global average pooling would demonstrate its contribution to feature representation learning and overall model robustness. Ultimately, a well-executed ablation study provides valuable insights into the architectural design and the interplay of different parts within a model, contributing towards a deeper understanding of its strengths and weaknesses.
Future Work#
The paper’s ‘Future Work’ section would ideally address several key limitations. Improving the efficiency of the alternating optimization framework is crucial, potentially through exploring single-phase approaches to avoid the trivial solution problem. Addressing the limitations of relying solely on Barlow Twins loss is vital; the paper should investigate alternative or complementary loss functions to enhance robustness and address issues with limited data. Expanding to handle more diverse and complex multimodal scenarios is another critical area; the current method’s generalization capabilities need further evaluation and potential refinement. Finally, a thorough discussion on how to reduce the performance gap between unsupervised and supervised methods would strengthen the paper, suggesting potential improvements in architecture or training strategies. Exploring the potential of transformers could be a fruitful direction to pursue.
More visual insights#
More on figures
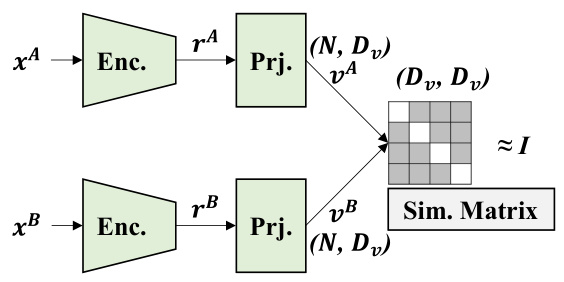
The Barlow Twins method is a self-supervised learning method. The diagram shows two inputs, A and B, which pass through an encoder network to produce representations rA and rB. These representations then go through a projector network to produce embedding vectors vA and vB. The similarity matrix between vA and vB is calculated, and the loss function aims to make this similarity matrix close to the identity matrix, thereby encouraging the model to learn good representations that are similar for similar inputs and dissimilar for dissimilar inputs.
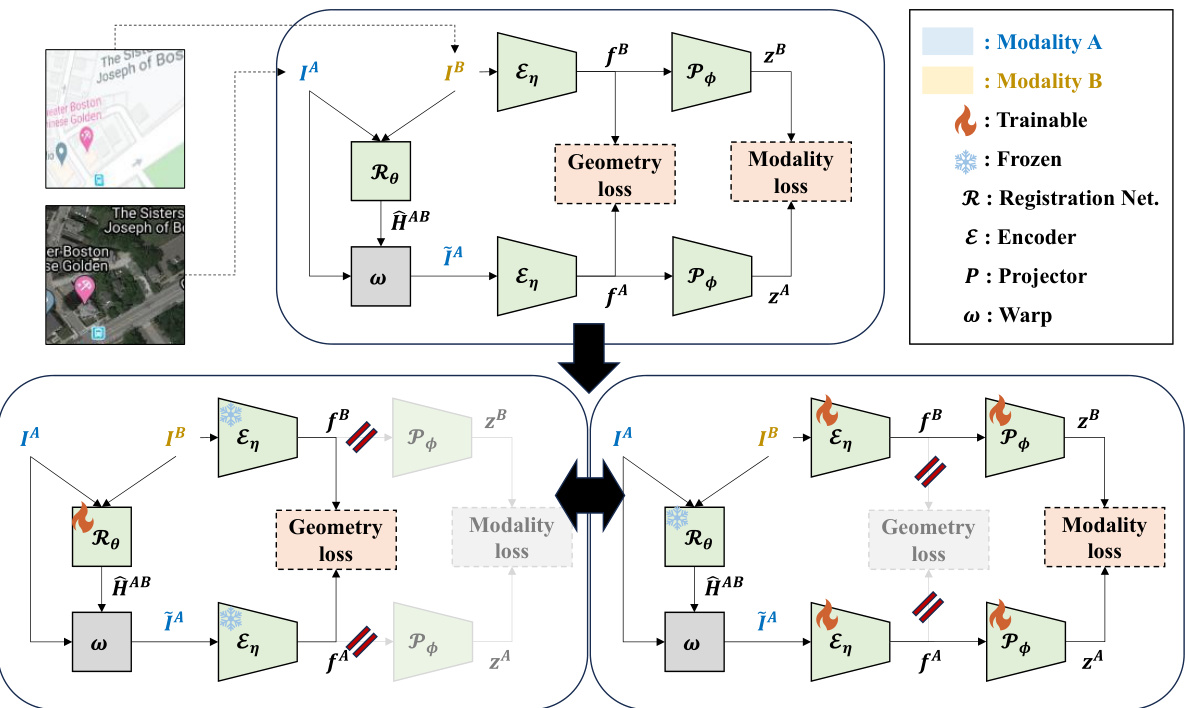
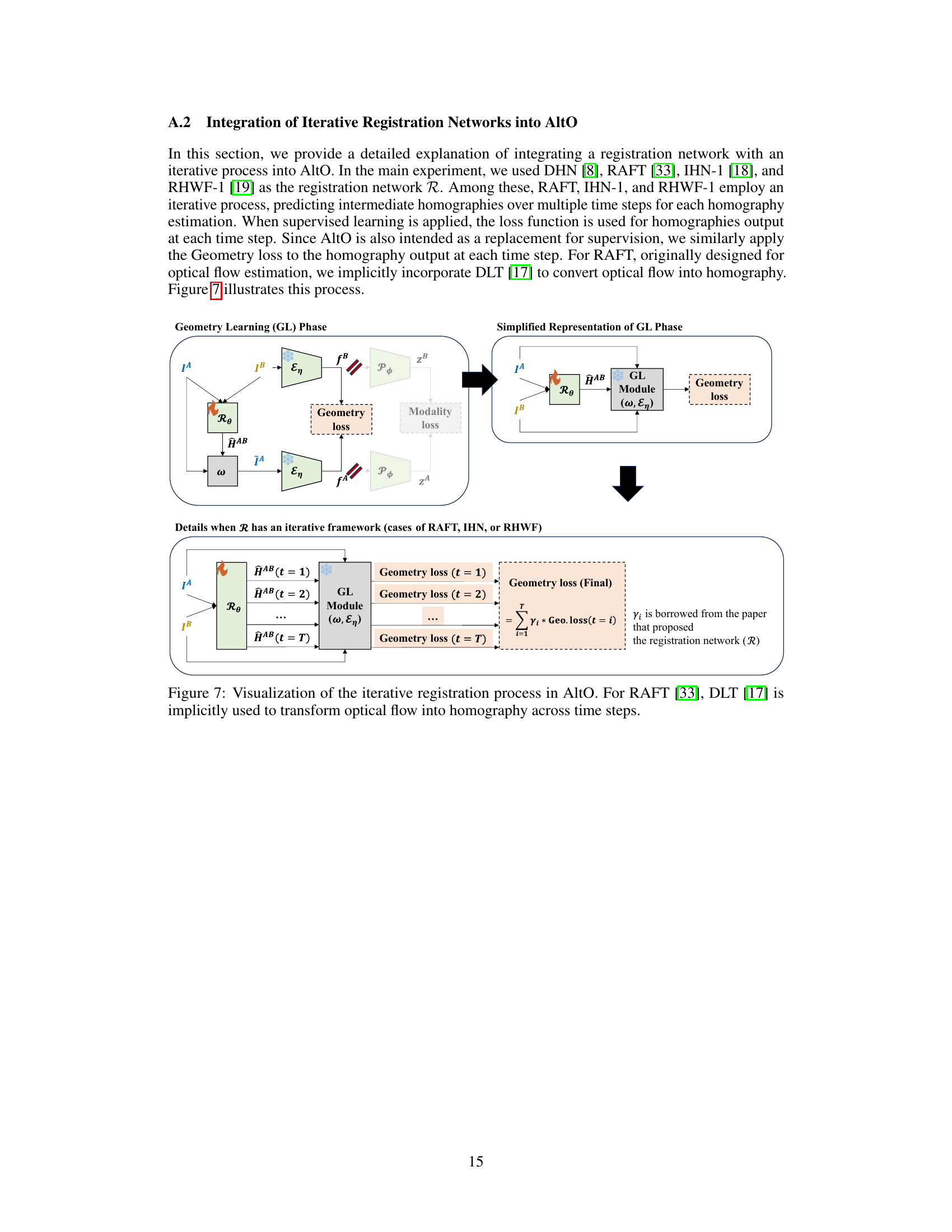
This figure illustrates the architecture of the AltO framework. The upper diagram provides a static overview of the network, showing the input images (from modalities A and B), the registration network (R), the encoder (E), the projector (P), the warping function (ω), and the loss functions (Geometry and Modality). The lower diagrams demonstrate the two-phase alternating optimization process. In the Geometry Learning (GL) phase, the registration network is trained to align the warped moving image with the fixed image. In the Modality-Agnostic Representation Learning (MARL) phase, the encoder and projector are trained to learn a modality-invariant representation. The figure highlights which components are trainable and frozen in each phase.

This figure shows example image pairs from the three datasets used in the paper’s experiments: Google Map, Google Earth, and Deep NIR. Each dataset presents a different type of multimodal image pair, showcasing the challenges of homography estimation in diverse scenarios. Google Map pairs show satellite imagery and corresponding maps, Google Earth pairs show the same area at different times of the year, and Deep NIR pairs show images from RGB and NIR sensors.

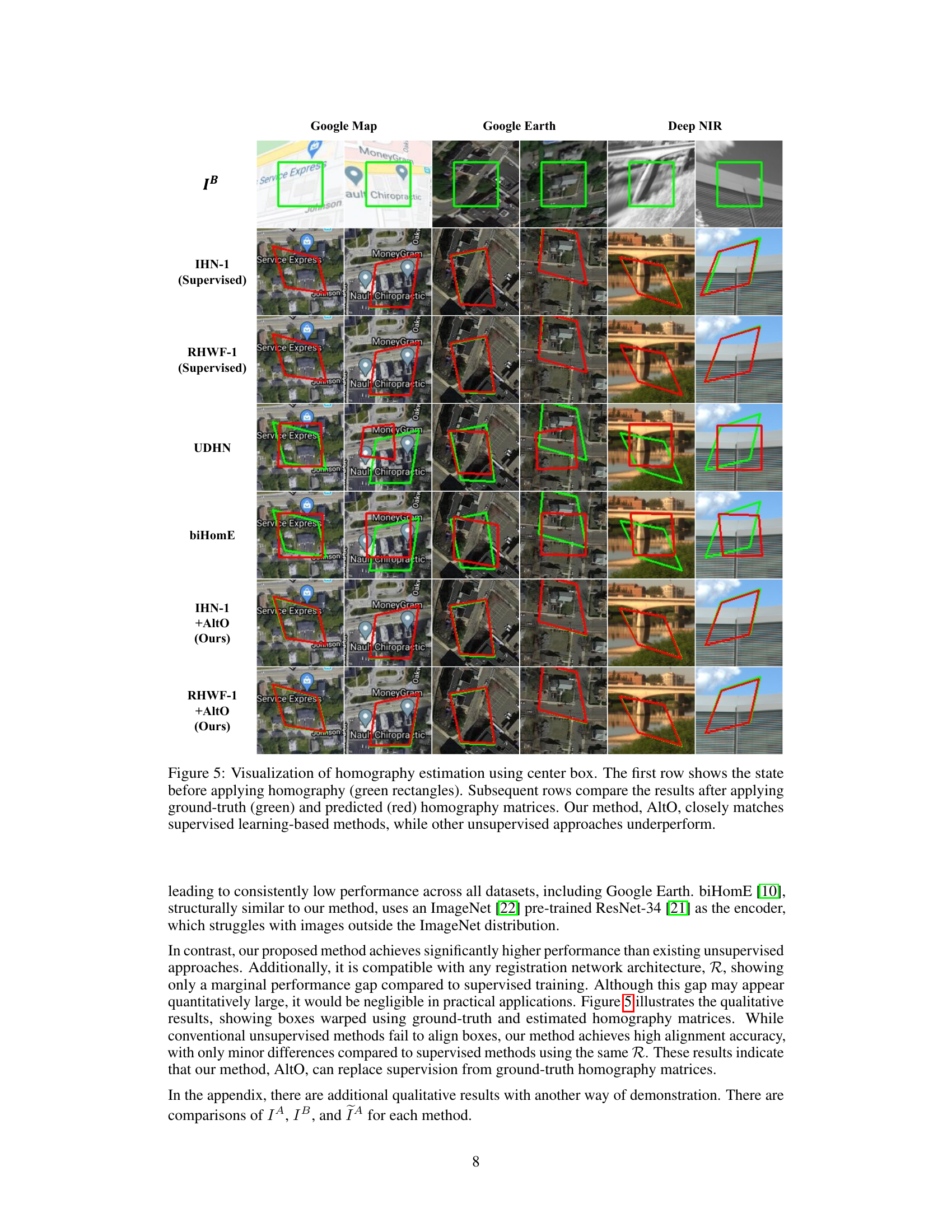
This figure visualizes the performance of different homography estimation methods on three datasets (Google Map, Google Earth, and Deep NIR). Each column represents a dataset. The top row shows the original images with a green box marking a region of interest. Subsequent rows show the warped result of applying ground truth homography (green box) and homography predicted by each method (red box). The results demonstrate that AltO achieves comparable performance to supervised methods, while other unsupervised approaches show significant misalignment.

This figure visualizes the results of homography estimation on three different datasets (Google Map, Google Earth, and Deep NIR). The first row shows the original moving images (IA). The second row shows the corresponding fixed images (IB) that the moving images should be aligned to. The remaining rows display the warped moving images (ĨA), which have been transformed using the predicted homography matrices from different methods (including supervised learning baselines and the proposed AltO method). By comparing the warped images (ĨA) with the fixed images (IB), one can visually assess the accuracy of each method in aligning images, highlighting the superior performance of the AltO method compared to unsupervised learning baselines.

This figure illustrates the architecture of the proposed AltO framework. The upper diagram provides a high-level overview of the network, showing the input images (from modalities A and B), the registration network (R) that predicts the homography matrix, and the two loss functions (geometry and modality). The lower diagrams show the two alternating phases: Geometry Learning (GL) and Modality-Agnostic Representation Learning (MARL). In the GL phase, the registration network is trained to align the images by minimizing the geometry gap, while in the MARL phase, the encoder and projector are trained to learn a modality-agnostic representation. This alternating optimization strategy helps to address both the geometry and modality gaps in multimodal image pairs.
More on tables
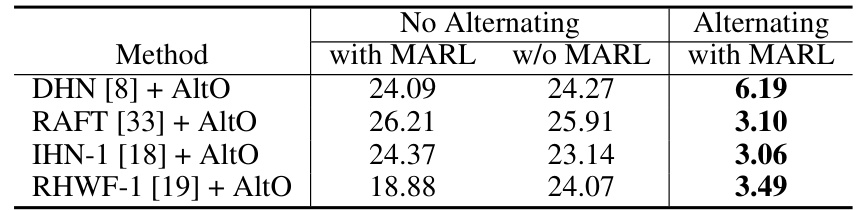
This table presents the Mean Average Corner Error (MACE) results for different methods, comparing the performance with and without alternating optimization and Modality-Agnostic Representation Learning (MARL). The results show a significant improvement in MACE when alternating optimization is used, highlighting its effectiveness in addressing the trivial solution problem and improving the accuracy of homography estimation.
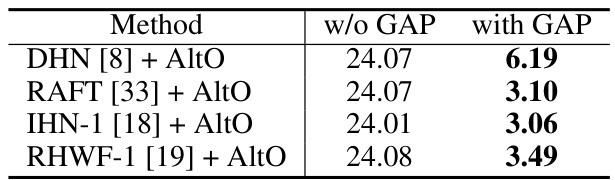
This table presents the results of an ablation study that investigates the impact of global average pooling (GAP) on the performance of the proposed AltO method. The study uses the Google Map dataset [11] and compares the mean average corner error (MACE) for four different registration networks (DHN [8], RAFT [33], IHN-1 [18], and RHWF-1 [19]) with and without GAP. The results show that GAP significantly improves performance, reducing MACE values substantially across all four networks.

This table presents the results of an ablation study that investigates the impact of different loss functions on the performance of the proposed AltO framework. Specifically, it explores various combinations of Geometry loss and Modality loss, using three popular contrastive loss functions (Barlow Twins, InfoNCE, VIC-Reg) and Mean Squared Error (MSE). The results, measured by Mean Average Corner Error (MACE), show the effectiveness of the Barlow Twins loss for both Geometry and Modality, while other loss functions result in lower performance.
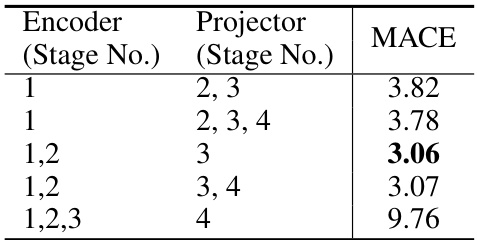
This table presents the results of an ablation study on the architecture of the encoder and projector in the proposed AltO framework. Different combinations of ResNet stages were used for the encoder and projector, and the resulting Mean Average Corner Error (MACE) is reported. The goal was to determine the optimal configuration for both components to achieve the best performance in homography estimation.
Full paper#