↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current graph autoencoders (GAEs) primarily rely on self-correlation for reconstructing graph structures from node embeddings. However, this approach has limitations, especially when dealing with specific graph features such as islands, symmetrical structures, and directed edges, particularly in smaller or multiple graph contexts. Self-correlation also limits the optimization process due to the restricted space and unbalanced population in the adjacency matrix.
To address these limitations, the authors propose GraphCroc, a novel GAE model that employs a cross-correlation mechanism. GraphCroc uses a mirrored encoder-decoder architecture, allowing for flexible encoder designs tailored to specific tasks while ensuring robust structure reconstruction. It also incorporates a loss-balancing strategy to mitigate representation bias during optimization. Experiments demonstrate that GraphCroc significantly outperforms existing self-correlation-based GAEs in graph structure reconstruction across various graph datasets. The study further investigates the potential of GAEs as attack surfaces by leveraging adversarial attacks in the latent space. GraphCroc’s superior performance and the vulnerability analysis makes it a significant contribution to the field of graph representation learning.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses limitations of existing graph autoencoders, proposing a novel cross-correlation approach that significantly improves graph structure reconstruction, particularly for complex scenarios involving multiple or smaller graphs. This opens avenues for enhanced graph representation in various applications and provides valuable insights for researchers in graph neural networks and related fields. The vulnerability analysis further highlights a potential attack surface for future research, adding a crucial security perspective to GAE applications.
Visual Insights#

This figure shows two examples of topologically symmetric graphs. A topologically symmetric graph is defined as having its structure and node features symmetric either along a specific axis or around a central node. The left graph demonstrates axis symmetry, where node features and connections are symmetric about an axis. The right graph illustrates centrosymmetry, characterized by a central pivot node and symmetric node features and connections around it.

This table presents the Area Under the Curve (AUC) scores for reconstructing the adjacency matrix in various graph tasks using different global graph autoencoder (GAE) methods. The methods are categorized into self-correlation and cross-correlation approaches, with both including several established and novel techniques. The table helps to compare the performance of different GAE methods in terms of their ability to accurately reconstruct graph structures. Higher AUC scores indicate better performance.
In-depth insights#
Cross-Correlation GAEs#
Cross-correlation graph autoencoders (GAEs) represent a significant advancement in graph representation learning. Unlike traditional self-correlation GAEs, which primarily leverage the correlation between node embeddings within the same space, cross-correlation GAEs utilize correlations between node embeddings from separate spaces. This subtle yet powerful change offers several key advantages. First, it significantly enhances the model’s ability to represent complex graph structures such as islands, symmetrical arrangements, and directed edges. Second, the expanded search space afforded by cross-correlation leads to smoother and more efficient optimization, improving convergence during training. Finally, the decoupling inherent in cross-correlation allows for greater flexibility in encoder design, enabling adaptation to various downstream tasks without compromising structural reconstruction capabilities. This makes cross-correlation GAEs a promising area of research for improving the accuracy and efficiency of graph representation learning, particularly in scenarios involving diverse and complex graph structures.
GraphCroc: Design#
The design of GraphCroc centers on addressing limitations of existing Graph Autoencoders (GAEs). Cross-correlation, a key innovation, replaces the self-correlation mechanism in the decoder, enabling more accurate representation of diverse graph structures like islands and directed graphs. This is achieved through two parallel decoders generating separate node embeddings (P and Q), whose product forms the reconstruction. The encoder’s design is kept flexible, allowing adaptation to various downstream tasks. A mirrored encoder-decoder architecture facilitates robust reconstruction. To handle the class imbalance inherent in graph data, a loss-balancing strategy is employed. Overall, GraphCroc’s design prioritizes flexibility and accuracy in graph structure reconstruction by strategically addressing the shortcomings of self-correlation-based GAEs.
Structural Recon Analysis#
The section on ‘Structural Recon Analysis’ would likely delve into the methods used to reconstruct graph structures from learned node embeddings. This is a core challenge in graph autoencoders (GAEs). The analysis would likely compare the representational power of different approaches, particularly self-correlation versus cross-correlation. A key focus would be identifying limitations of self-correlation in accurately representing various graph features like islands or symmetrical structures. The authors would likely present theoretical arguments and possibly mathematical proofs to support their claims, showing why cross-correlation offers a more robust and flexible reconstruction. This analysis would set the stage for introducing their proposed GAE model, demonstrating its ability to overcome the limitations identified in the analysis and achieve superior performance on structural reconstruction tasks.
Graph Classification#
Graph classification, a crucial task in graph mining, focuses on assigning labels to entire graphs based on their structural properties. Effective graph representation is paramount; techniques like graph kernels or graph neural networks (GNNs) are frequently employed to encode graph structure into feature vectors suitable for classification algorithms. However, challenges remain. Scalability is a major concern, as many graph classification methods struggle with large graphs. Furthermore, handling diverse graph structures (e.g., directed, undirected, attributed) requires robust and adaptable techniques. Generalizability is another key aspect; a classifier should perform well on unseen graphs from a variety of distributions. The choice of classification algorithm (e.g., support vector machines, random forests) also plays a crucial role, with model selection and hyperparameter tuning critical for optimal performance. Recent advancements increasingly involve self-supervised learning and graph autoencoders, leveraging latent representations to learn effective graph embeddings and improve generalizability. Despite these ongoing developments, research in graph classification remains very active, driven by the need for improved accuracy, efficiency, and explainability in various application domains.
Adversarial Attacks#
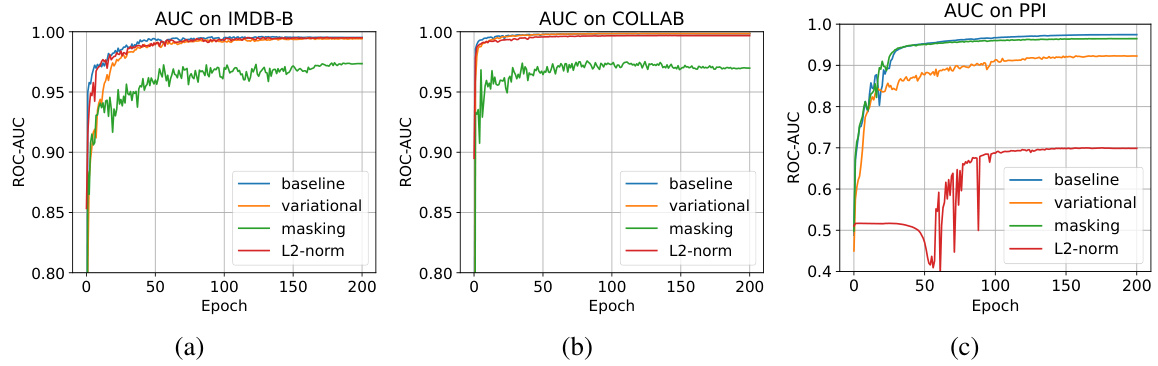
The section on adversarial attacks explores the vulnerability of Graph Autoencoders (GAEs) to malicious manipulation. The core idea is that by subtly altering the latent representations of graphs, an attacker could potentially mislead the GAE’s reconstruction or downstream tasks. This is a significant concern, as GAEs are increasingly used in security-sensitive applications. The paper investigates the effectiveness of different attack strategies, such as injecting random noise or using more sophisticated methods like Projected Gradient Descent (PGD) and Carlini & Wagner (C&W) attacks. A key finding is that even small perturbations in the latent space can have a substantial impact on the GAE’s output, highlighting the need for robust and resilient GAE architectures. The research also demonstrates that adversarial attacks on GAEs could be more efficient compared to those directly on graph structures due to the inherent complexity and discreteness of graph data. Further research is needed to develop effective defense mechanisms against such attacks, potentially involving improved training methodologies, more resilient model architectures or the development of specialized detection techniques. This is a crucial area for future work, as the widespread adoption of GAEs necessitates understanding and addressing their vulnerabilities.
More visual insights#
More on figures

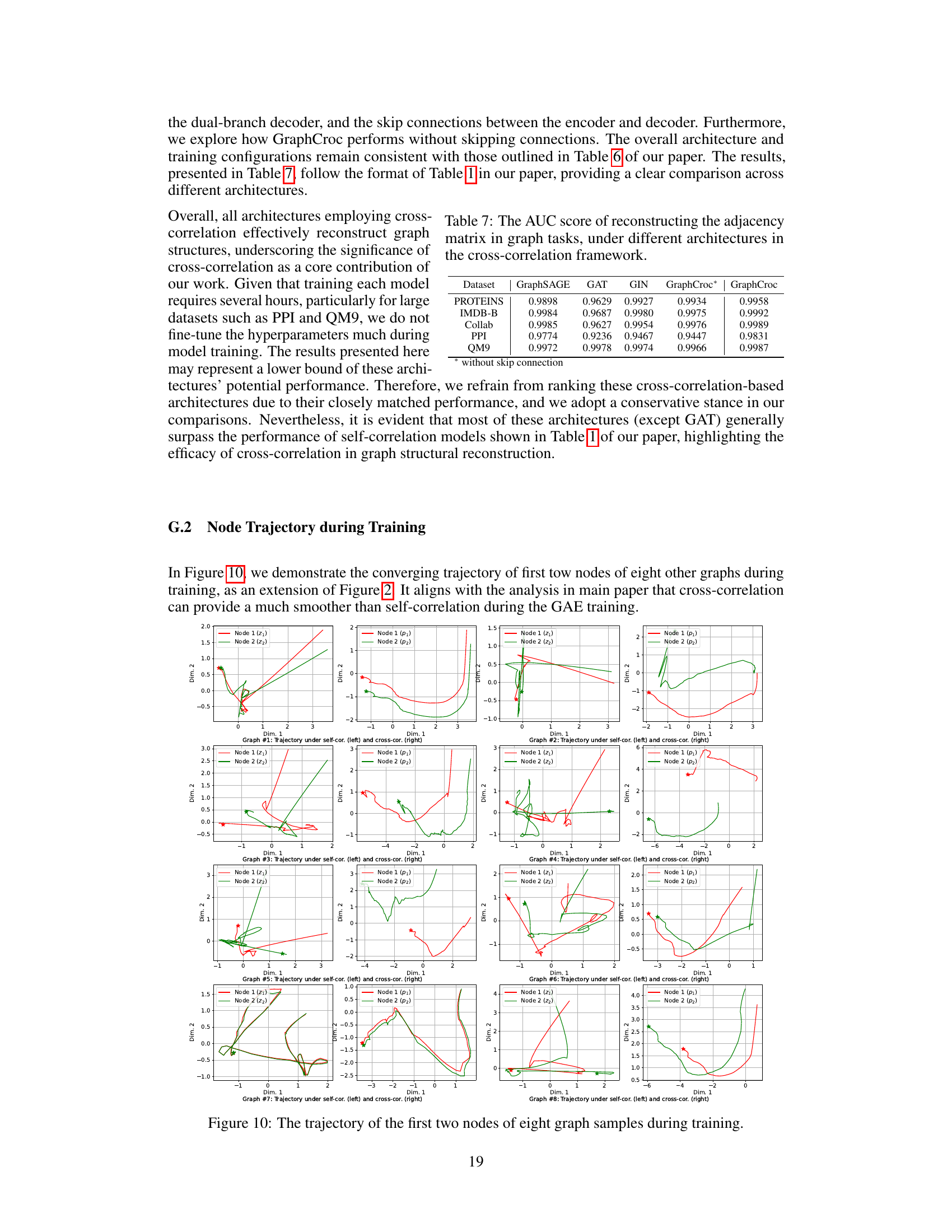
This figure compares self-correlation and cross-correlation methods for graph autoencoder training on a subset of the PROTEINS dataset. It visualizes the trajectory of node embeddings during training for both methods, showing that cross-correlation leads to a smoother and more efficient convergence. The figure also shows the loss curves and the distribution of diagonal elements (representing self-loops) during training, further supporting the advantages of cross-correlation.
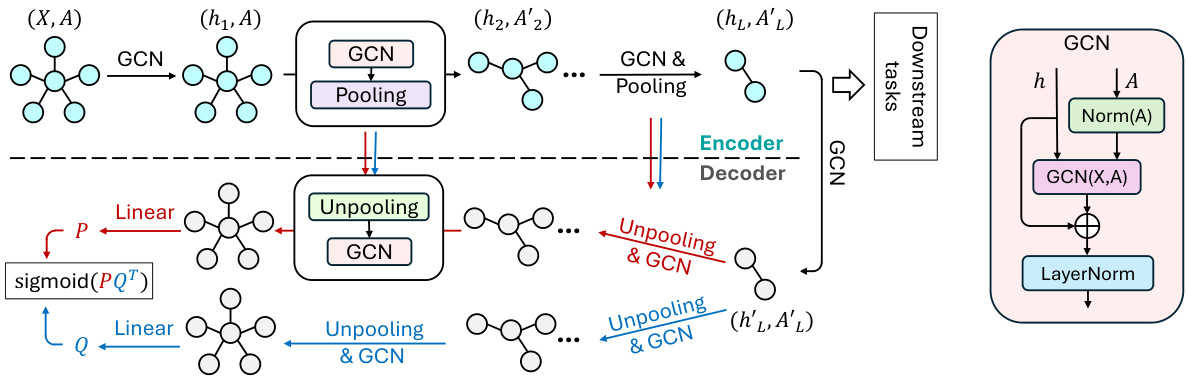
This figure illustrates the architecture of the GraphCroc model, which is a new Graph Autoencoder (GAE). It consists of an encoder and two mirrored decoders that work in parallel. The encoder is a Graph Neural Network (GNN) that takes as input the graph’s node features and adjacency matrix. It then processes the information through several layers of GCN (Graph Convolutional Network) and pooling operations. The output of the encoder is a latent representation of the graph. Each decoder takes the latent representation as input, along with the node features and adjacency matrix, and reconstructs the adjacency matrix using cross-correlation between node embeddings generated by two parallel GCN paths. The decoders have a U-net like structure, with skip connections between encoder and decoder layers to improve performance. In addition, layer normalization and skip connections are also used to enhance the model’s performance. The figure also shows the GCN module, highlighting the key components such as layer normalization and skip connections.

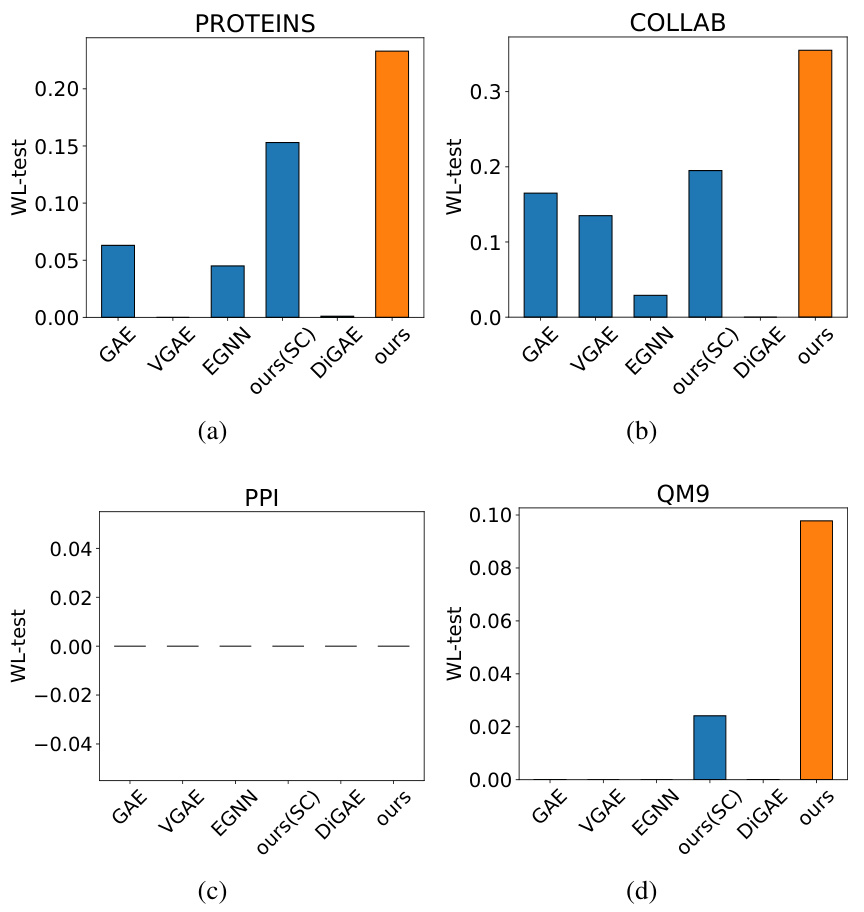
This figure displays the results of the Weisfeiler-Lehman (WL) test, a graph isomorphism test, performed on various Graph Autoencoder (GAE) methods for the IMDB-B dataset. The WL-test assesses how well each GAE method reconstructs the graph structure. The higher the bar, the better the reconstruction performance, indicating that GraphCroc (the orange bar) performs best at reconstructing graph structures compared to other methods.
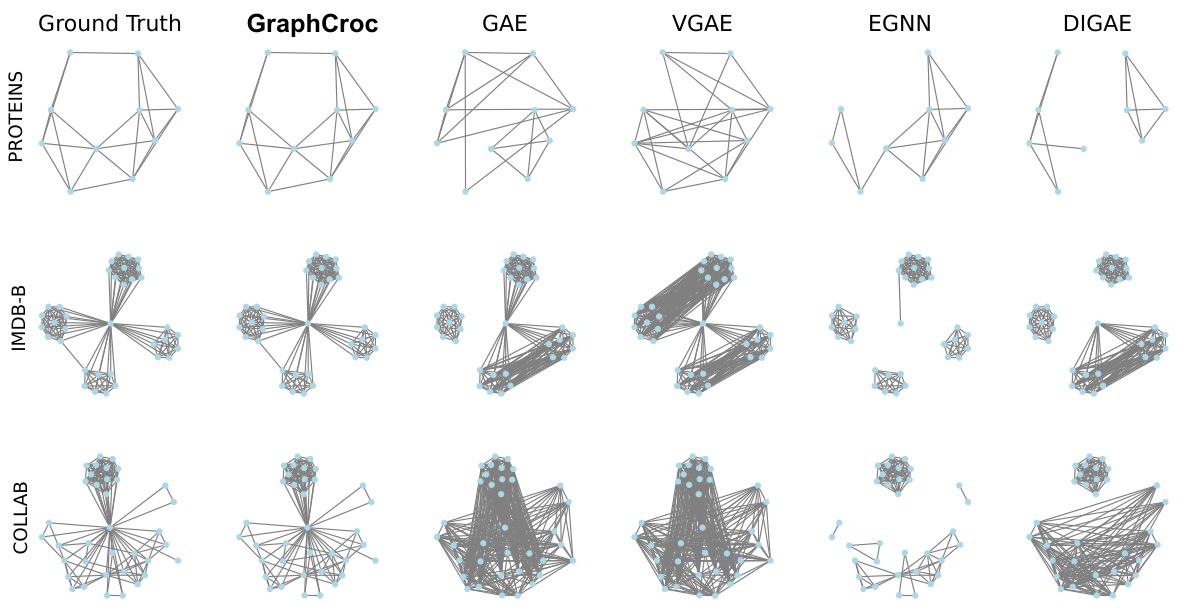
This figure visualizes the reconstruction of several graphs from different datasets (PROTEINS, IMDB-B, and COLLAB) by various graph autoencoder (GAE) models. The ‘Ground Truth’ column shows the original graphs. The remaining columns show the reconstruction of the same graphs by GraphCroc and several other GAE methods (GAE, VGAE, EGNN, DIGAE). The figure demonstrates the superior performance of GraphCroc in accurately reconstructing the graph structures compared to other methods.

This figure compares the training process of self-correlation and cross-correlation methods on a subset of the PROTEINS dataset. It shows the trajectories of node embeddings during training (using PCA for visualization), the BCE loss curves, and the distributions of diagonal elements (representing self- and cross-correlations) over iterations. The results highlight that cross-correlation leads to a smoother optimization process and better reconstruction results compared to self-correlation.
This figure visualizes the reconstruction results of different graph autoencoder (GAE) models on three graph datasets: PROTEINS, IMDB-B, and COLLAB. The ‘Ground Truth’ column shows the original graph structures. Subsequent columns display the reconstructed graphs generated by GraphCroc (the proposed model), GAE, VGAE, EGNN, and DiGAE. The figure highlights the differences in reconstruction accuracy between the various GAE models, demonstrating GraphCroc’s superior performance in capturing the original graph structures.
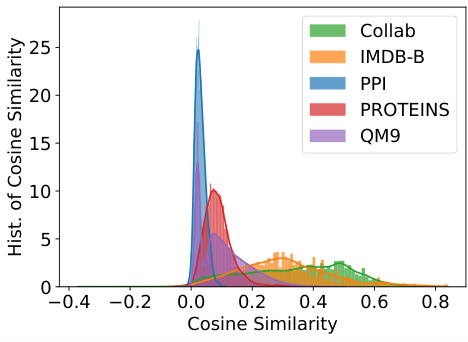
This figure shows the distribution of cosine similarity between the two node embeddings (P and Q) generated by the GraphCroc model’s decoder for various graph datasets (COLLAB, IMDB-B, PPI, PROTEINS, QM9). The x-axis represents the cosine similarity, ranging from -0.4 to 0.8, and the y-axis represents the frequency or count of cosine similarity values. Each dataset’s distribution is shown with a different color. The low cosine similarity values across datasets indicate that the two embeddings are effectively kept independent, as intended by the GraphCroc’s design which uses cross-correlation instead of self-correlation.
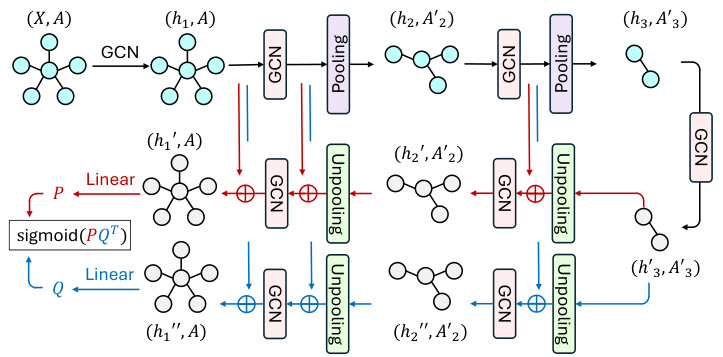
This figure illustrates the architecture of GraphCroc, a graph autoencoder model. It uses a U-Net-like structure with an encoder and a two-branched decoder. The encoder is a GNN (Graph Neural Network) that processes the graph structure and node features, outputting a latent representation. The decoder then uses this representation to reconstruct the adjacency matrix of the graph. It’s noteworthy that the decoder uses cross-correlation (instead of self-correlation) and is designed as a mirrored version of the encoder. This means that the decoder reverses the steps of the encoder, gradually reconstructing the graph structure from the compressed representation. Skip connections and layer normalization are used to improve performance.

This figure compares the training process of self-correlation and cross-correlation methods using the PROTEINS dataset. Subfigures (a) and (b) show the trajectories of the first two node embeddings in a sample graph during training, visualizing the optimization process using PCA and smoothing. (c) plots the binary cross-entropy (BCE) loss over training iterations, demonstrating faster convergence with cross-correlation. (d) displays the distribution of diagonal elements (self-correlation and cross-correlation) over iterations, further highlighting the differences in optimization behavior.
This figure compares the training process of self-correlation and cross-correlation methods on a subset of the PROTEINS dataset. It visualizes the trajectory of node embeddings during training using PCA for dimensionality reduction, showing how cross-correlation leads to smoother and more efficient convergence. The figure also displays the BCE loss and the distribution of diagonal elements (self-correlation vs. cross-correlation) over training iterations.
This figure compares the training process of self-correlation and cross-correlation methods on a subset of the PROTEINS dataset. It shows the trajectory of node embeddings during training, the BCE loss over iterations, and the distribution of diagonal elements (self-correlation vs. cross-correlation). The results suggest that cross-correlation leads to a smoother optimization process and better reconstruction.
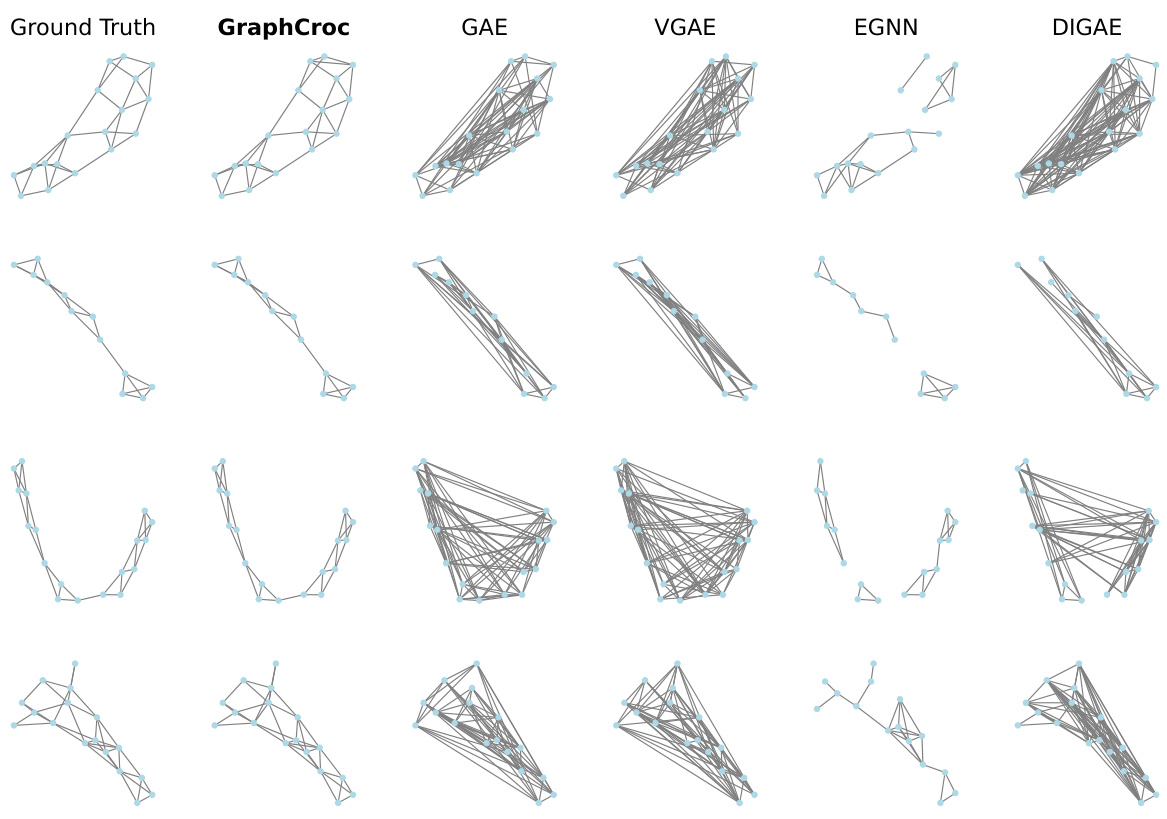
This figure visualizes the reconstruction results of different graph autoencoder models on three distinct graph datasets: PROTEINS, IMDB-B, and COLLAB. Each row represents a different graph from the dataset. The ‘Ground Truth’ column shows the original graph structure. The remaining columns display reconstructions generated by various models: GraphCroc (the proposed model), GAE, VGAE, EGNN, and DiGAE. The visualization allows for a qualitative comparison of the different models’ abilities to accurately reconstruct the graph structure, revealing the strengths and weaknesses of each approach in preserving the original connectivity patterns.
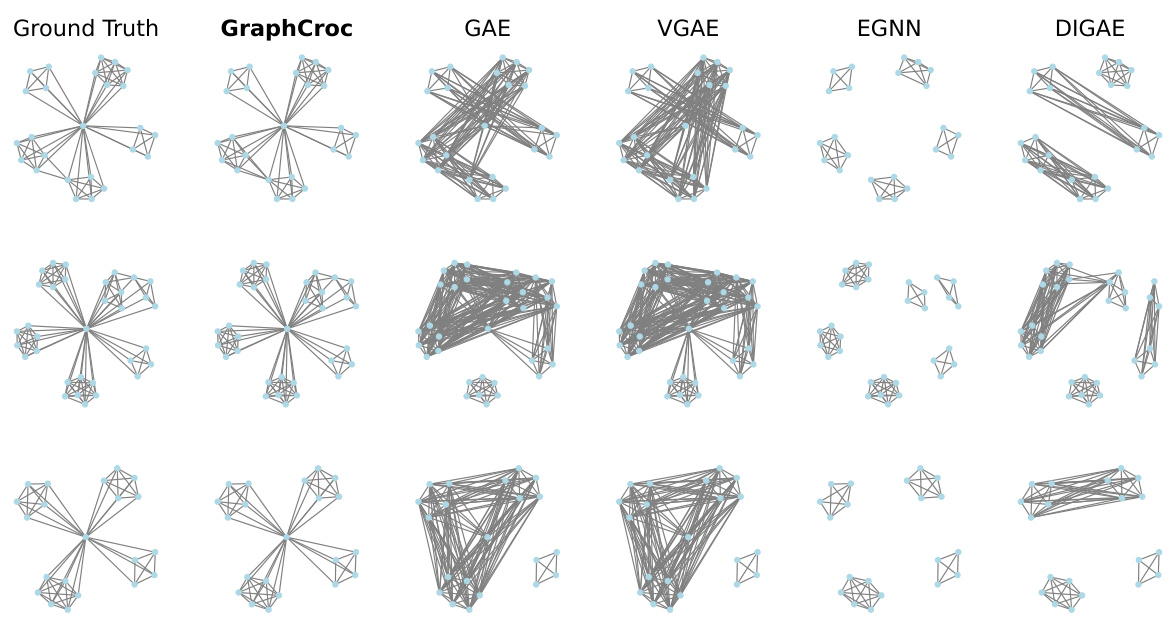
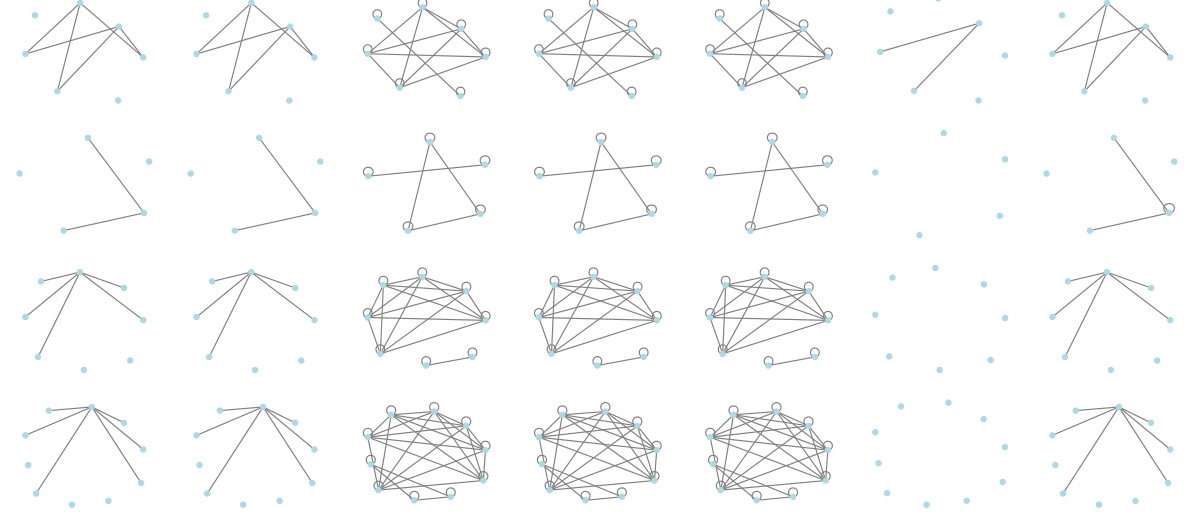
This figure visualizes the graph reconstruction performance of various graph autoencoder (GAE) models on graphs with symmetric structures and no self-loops. The ‘Ground Truth’ column shows the original graphs. The ‘GraphCroc’ column demonstrates the reconstruction using the proposed GraphCroc model. The remaining columns illustrate the reconstruction results of other GAE models, including GAE, VGAE, EGNN, and DiGAE. The visualization allows for a direct comparison of how accurately each model reconstructs the specific structural characteristics of these types of graphs. It highlights the superior performance of GraphCroc in preserving the symmetric structure and the absence of self-loops, while other models struggle with this task, sometimes misrepresenting the graph significantly.

This figure visualizes the reconstruction results of different graph autoencoder models on three different graph datasets (PROTEINS, IMDB-B, and COLLAB). For each dataset, several example graphs are shown. The ‘Ground Truth’ column displays the original graph structure. The remaining columns showcase the reconstructed graphs produced by GraphCroc and other GAE methods (GAE, VGAE, EGNN, DIGAE). The visualization allows for a qualitative comparison of the different models’ ability to accurately reconstruct graph structures, revealing that GraphCroc generally performs better than other models at recovering the original graph structure.
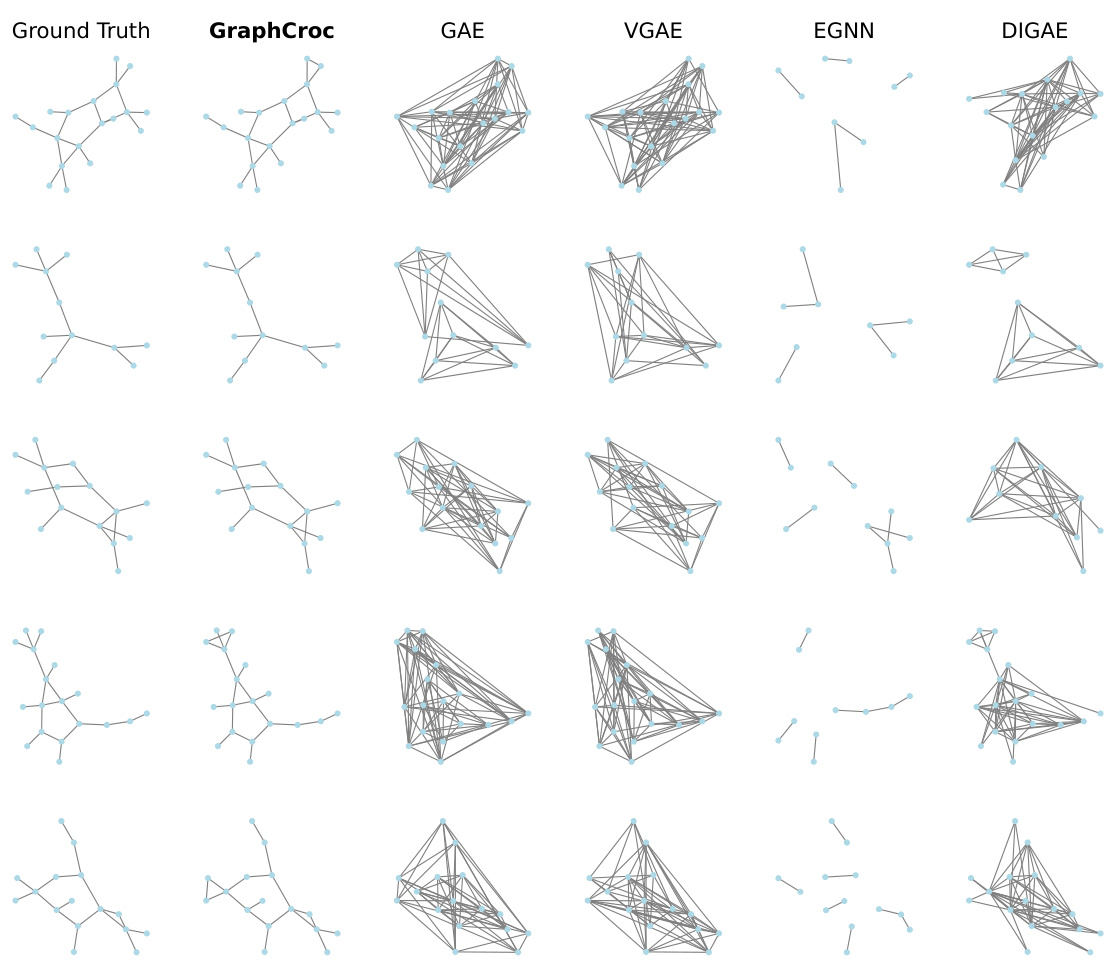
This figure visualizes the reconstruction results of different graph autoencoder models on three different graph datasets: PROTEINS, IMDB-B, and COLLAB. Each row represents a different dataset, and each column represents a different model: Ground Truth, GraphCroc, GAE, VGAE, EGNN, and DiGAE. The visualizations show the original graph structure (Ground Truth) and how each model reconstructs the graph from the node embeddings. The goal is to compare the accuracy and visual fidelity of the reconstructions across various models, especially highlighting the superior performance of GraphCroc.
More on tables

This table presents the results of graph classification experiments comparing GraphCroc with several other state-of-the-art GNN methods. The table shows the accuracy of different models on three graph classification datasets (PROTEINS, IMDB-B, and COLLAB) using two training strategies: 10 epochs of fine-tuning and 100 epochs of training. GraphCroc’s encoder is used, followed by a 3-layer classifier.

This table presents the Area Under the Curve (AUC) scores for reconstructing the adjacency matrix in various graph tasks using different Global Graph Autoencoder (GAE) methods. It compares self-correlation based methods (naïve GAE, variational GAE, L2-norm EGNN, and GraphCroc with self-correlation) against cross-correlation based methods (DiGAE and GraphCroc with cross-correlation). The best and second-best performing methods for each task are highlighted.

This table presents the Area Under the Curve (AUC) scores achieved by two different graph autoencoder models, DiGAE and GraphCroc, in the task of reconstructing the adjacency matrices of directed graphs. The results are broken down by dataset (Cora_ML with average node counts of 41 and 77, and CiteSeer with an average of 16 nodes). The AUC score measures the model’s ability to accurately predict the connections between nodes in the graph. Higher AUC scores indicate better performance.

This table presents the Area Under the Curve (AUC) scores for reconstructing the adjacency matrix of various graphs using different Global Graph Autoencoder (GAE) methods. It compares self-correlation methods (naïve GAE, variational GAE, L2-norm EGNN, and GraphCroc with self-correlation) against cross-correlation methods (DiGAE and GraphCroc with cross-correlation). The best and second-best AUC scores for each dataset are highlighted.

This table compares the performance of various Graph Autoencoder (GAE) models on the task of reconstructing the adjacency matrix of graphs. It includes both self-correlation and cross-correlation based methods, showing the Area Under the Curve (AUC) score for each model on five different graph datasets (PROTEINS, IMDB-B, COLLAB, PPI, QM9). The table highlights the superior performance of the proposed GraphCroc model, particularly when using the cross-correlation approach.
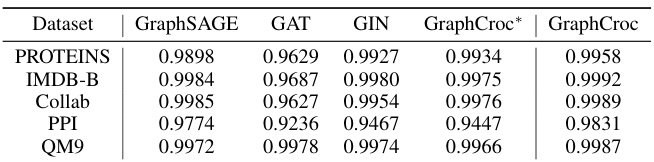
This table presents the Area Under the Curve (AUC) scores achieved by various Graph Autoencoder (GAE) models in reconstructing the adjacency matrix of graphs. The models are categorized into self-correlation and cross-correlation methods, with different decoding strategies used. The table compares the performance of existing GAE models (naïve GAE, variational GAE, L2-norm EGNN) with the proposed GraphCroc model using both self-correlation and cross-correlation. The best and second-best AUC scores for each dataset are highlighted.
Full paper#